行为两两NQD随机变量阵列加权和的完全收敛性

章茜

(浙江机电职业技术学院 数学教研室， 浙江 杭州 310053)

行为两两NQD随机变量阵列加权和的完全收敛性

章茜

(浙江机电职业技术学院 数学教研室， 浙江 杭州 310053)

负相依在统计分析和可靠性理论中有着广泛的应用.研究了一类行为两两NQD随机变量阵列加权和的完全收敛性.利用矩不等式和有效的截尾方法,建立了行为两两NQD随机变量阵列加权和的完全收敛性的充要条件,从而推广了吴群英等建立的关于一类NA随机变量序列的完全收敛性的结论.

行为两两NQD阵列;加权和;完全收敛性

0 引 言

定义1对于随机变量X和Y,若∀x,y∈R,有

P(X≤x,Y≤y)≤P(X≤x)P(Y≤y),

则称X和Y是NQD(negatively quadrant dependent)的;若∀i≠j,Xi和Xj是NQD的, 则称随机变量序列{Xn,n≥1}是两两NQD列.

上述定义由统计学家LEHMAMN[1]于1966年提出. 两两NQD列是一类非常广泛的随机变量序列, 例如两两独立的随机变量列以及NA(negative association)[2]列就是其特例. 因此, 对两两NQD列的研究具有重要的理论意义和应用价值. 目前,关于两两NQD列的极限研究已有许多结果,详见文献[3-7].近年来,GUT等[8]获得了一类独立同分布且均值为零的随机变量序列的完全收敛性,吴群英等[9]将其推广到NA随机变量序列的情形.受上述文献启发,本文将文献[9]的定理1.3推广到更为一般的行为两两NQD随机变量阵列加权和的情形.

定义2随机变量阵列{Xni,i≥1,n≥1}被随机变量X控制是指:如果存在一常数C>0,使得对任意的n≥1,i≥1,x≥0,有P(|Xni|≥x)≤CP(|X|≥x).

本文中,an≪bn表示存在常数c>0,使得对所有n≥1, 有an≤cbn.an≈bn表示对所有n≥1, 有an≪bn以及bn≪an.I(A)表示集合A的示性函数,#A表示集合A中元素的个数.

1 引 理

引理1[3]设随机变量X和Y是NQD的,则

(1)EXY≤EXEY;

(2)对∀x,y∈R,有P(X>x,Y>y)≤P(X>x)P(Y>y);

(3)若f,g同为非降(或非增)函数,则f(X)与g(Y)仍为NQD的.

则有

引理3[7]令{Xn,n≥1}是两两NQD随机变量列, 那么对于任意的n≥1以及x≥0, 有

2 主要结果及证明

E|X|exp(lnα|X|)<∞

(1)

(2)

证明先证式(1)⟹式(2).

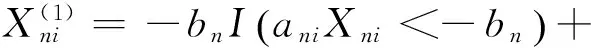
aniXniI(|aniXni|≤bn)+bnI(aniXni>bn),

(aniXni-bn)I(aniXni>n).

注意到

因此欲证式(2)，只需证明

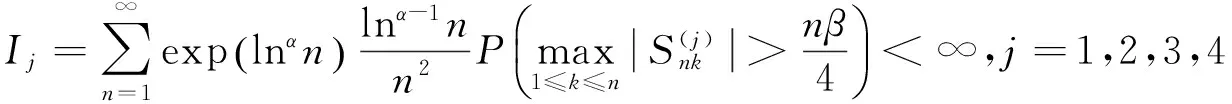
由EXni=0及Markov不等式，先证

E|X|exp(lnα|X|)<∞蕴含着

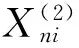
(至少存在2个k，使得ankXnk>bn).

则

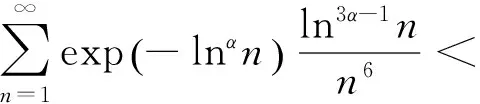
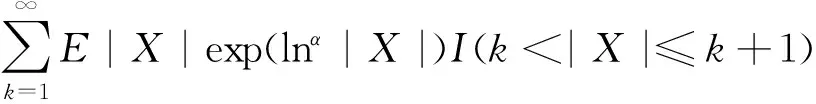
E|X|exp(lnα|X|)<∞.

现在, 证明式(2)⟹式(1). 显然,式(2)蕴含着

(3)

则有

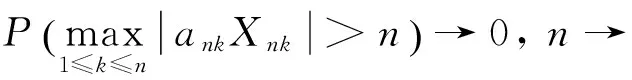
因此, 对于足够大的n，有

由引理1得{aniXni}仍然为两两NQD阵列. 由引理3,有

(4)

由式(3)及式(4), 有

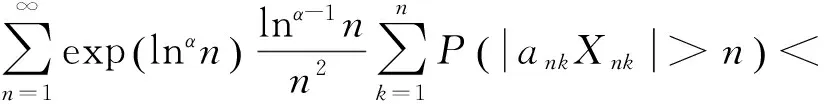
根据I4<∞的证明过程,

E|X|exp(lnα|X|)≈

证毕.

注文献[9]定理1.3描述的是一类NA随机变量序列的完全收敛性定理，本文将此定理推广到更一般的行为两两NQD随机变量阵列加权和的情形，在增加权条件的基础上，通过采用不同的截尾方法，亦得到了类似的结论.

[1]LEHMAMNEL.Someconceptsofdependence[J].AnnMathStat,1966,37:1137-1153.

[2] JOAG-DEVK, PROSCHAN F. Negative association of random variables with applications[J].Ann-Statist,1983(11):286-295.

[3] 吴群英.两两NQD列的收敛性质[J].数学学报,2002,45(3):617-624. WU Q Y. Convergence properties of pairwise NQD random sequences[J].ActaMathematicaSinica,2002,45(3):617-624.

[4] 陈平炎.两两NQD随机序列的Lr收敛性[J].数学物理学报:A辑,2008,28(3):447-453. CHEN P Y.Lrconvergence for pairwise NQD random variables[J].ActaMathematicaScientia:SerA,2008,28(3):447-453.

[5] 方炜，郭明乐.行为两两NQD阵列加权和的矩完全收敛性[J].工程数学学报,2013,30(5):761-772. FANG W, GUO M L. Complete moment convergence of weighted sums for arrays of row-wise pairwise NQD random variables[J].ChineseJournalofEngineeringMathematics,2013,30(5):761-772.

[6] 邱德华,甘师信.两两NQD列随机变量序列的完全收敛性[J].武汉大学学报:理学版,2013,59(3):285-290.

QIU D H, GAN S X. Complete convergence for sequence of pairwise NQD random variables[J].JournalofWuhanUniversity:NaturalSciencesEdition,2013,59(3):285-290.

[7] MI-HWA K. On Complete convergence for weighted sums of pairwise negatively quadrant dependent sequences[J].CommunicationsofKoreanStatisticalSociety,2012,19(2):247-256.

[8] GUT A, STADTMULLER U. An intermediate Baum-Katz theorem[J].StatistProbabLett,2011(10):1486-1492.

[9] WU Q Y, JIANG Y Y. Complete convergence and complete moment convergence for negatively associated sequences of random variables[J].JournalofInequalitiesandApplications,2016(1):1-10.

[10] LI D L, RAO M B, WANG X C. Complete convergence of moving average processes[J].StatistProbabLett,1992(14):111-114.

ZHANG Qian

(Mathematics Teaching and Research Section, Zhejiang Institute of Mechanical and Electrical Engineering, Hangzhou 310053, China)

Negative dependence is important and widely used in multivariate statistical analysis and reliability theory. The purpose of this paper is to study a kind of complete convergence for weighted sums of pairwise negatively quadrant dependent (NQD) sequences withEX=0,E|X|exp(lnα|X|)<∞,α>1.By applying moment inequality and truncation methods, the sufficient conditions of complete convergence theorem of weighted sums for arrays of row-wise pairwise NDQ random variables are established, which extends to the case of weighted sums of pairwise negatively quadrant dependent sequences with imposing weighted condition. Our results generalize corresponding result obtained by WU et al.

arrays with row-wise pairwise negatively quadrant dependent sequences; weighted sums; complete convergence

O 211.4

：A

：1008-9497(2017)05-538-04

2016-10-06.

章茜(1984-)，ORCID:http://orcid.org/0000-0002-2955-4600，女，硕士，讲师，主要从事概率极限理论研究，E-mail：qiwa_007@163.com.

10.3785/j.issn.1008-9497.2017.05.007

Completeconvergenceforweightedsumsofarrayswithrow-wisepairwisenegativelyquadrantdependentsequences. Journal of Zhejiang University(Science Edition), 2017,44(5):538-541