基于改进节点电气介数的电网关键节点辨识

徐 岩，郅 静

（华北电力大学新能源国家重点实验室，保定 071000）

基于改进节点电气介数的电网关键节点辨识

徐 岩，郅 静

（华北电力大学新能源国家重点实验室，保定 071000）

为提高电力系统运行安全水平，提出一种基于改进节点电气介数的电网关键节点辨识方法。以线路功率变量与节点注入功率变量之间的功率灵敏度矩阵为基础，结合节点类型的不同，计算改进节点电气介数识别电网的关键节点。综合考虑节点移除造成的负荷损失和节点受到注入功率扰动时的电网加权潮流分布熵，定义节点重要性指标衡量节点在负荷供电和功率传输中的作用，对关键节点识别结果进行检验。改进节点电气介数计算简单，克服了以往方法中假设节点间功率按最短路径传输的不足，同时考虑了线路中潮流的方向性。在IEEE39节点系统中对该方法进行验证，结果表明利用改进节点电气介数可有效识别电网负荷供电和功率传输中的关键节点。

电力系统；关键节点；改进节点电气介数；负荷损失；加权潮流分布熵

Abstract:To improve the operation safety level of power system，an identification method of key nodes in power grid is put forward based on improved node electric betweenness.On the basis of the power sensitivity matrix between line pow⁃er variable and nodal injection power variable，the improved node electric betweenness is calculated to identify key nodes according to the different types of nodes.Considering the load loss caused by node removal and the weighted pow⁃er distribution entropy with node injection power disturbance，node importance index is defined to measure the node function during the load power supply and power transmission，which is further used to verify the identification results of key nodes.With simple calculation，the improved node electric betweenness overcomes the shortcomings of the tradi⁃tional indexes which assume that the power goes along the shortest path between nodes，and it also considers the direc⁃tion of power flow.The simulation in IEEE 39-node system shows that the improved node electric betweenness can effec⁃tively identify the key nodes during the load power supply and power transmission.

Key words:power system；key node；improved node electric betweenness；load loss；weighted power distribution en⁃tropy

电力系统大停电事故中源发性故障主要来源于线路开断或母线跳闸[1-2]，其中母线跳闸会直接导致相连线路的移除，极有可能造成负荷损失，影响电网功率传输，具有更大的破坏性[3-4]。因此，识别电网负荷供电和功率传输中的关键节点，对其进行重点监测和保护，可有效提高电网的供电可靠性和运行安全水平。

文献[5]利用加权拓扑模型，将节点介数较大的节点作为关键节点，但该方法假设母线间功率只按最短路径流动，与电网潮流传输特点不符。文献[6]利用潮流追踪计算节点功率介数，并依据节点过负荷时的潮流熵验证节点重要性，但潮流追踪计算复杂，同时该方法没有考虑节点在负荷供电中的作用。文献[7-8]在线路电气介数[9]的基础上定义了节点电气介数，但没有考虑线路上不同方向的功率叠加后会有抵消的现象。

针对现有方法的缺点，提出一种基于改进节点电气介数的电网关键节点辨识方法。以线路功率变量与节点注入功率变量之间的功率灵敏度矩阵为基础，考虑线路负载率、不同节点发电量和负荷水平的影响计算改进线路电气介数，并结合节点类型的不同，计算改进节点电气介数识别电网的关键节点。综合考虑节点移除造成的负荷损失和节点受到功率扰动时的加权潮流分布熵，定义节点重要性指标衡量节点在电网负荷供电和功率传输中的作用，对关键节点识别结果进行检验。改进节点电气介数计算简单，克服了以往方法假设节点间功率按最短路径传输的不足，同时考虑了线路中潮流的方向性。最后，在IEEE39节点系统中对该方法进行了验证。

1 改进节点电气介数

1.1 功率灵敏度

1.1.1 电流相关度系数矩阵

高压输电网络中线路的电抗值远远大于电阻值，因此分析计算中可以用电抗值代替阻抗值[10]。电网节点电压方程为

式中：IN为节点注入电流列向量（以流入节点的方向为正方向）；UN为节点电压列向量；YN为节点电纳矩阵。

电网线路电流与节点电压之间的关系为

式中：IB为线路电流列向量；YB为线路电纳矩阵；A为节点关联矩阵。节点电纳矩阵的逆矩阵为节点电抗矩阵XN，即根据式（1）和式（2）可得

根据式（3）可知，线路电流和节点注入电流之间为线性关系，定义C（λ）为电网相关度系数矩阵[11]，即

对于一个含有n个节点，b条线路的网络，C（λ）是b×n阶实数矩阵，C（λ）仅与网络参数及拓扑结构有关。以线路k为例，其电流相量Ik,B是各节点注入电流的线性组合，恶搞额且有

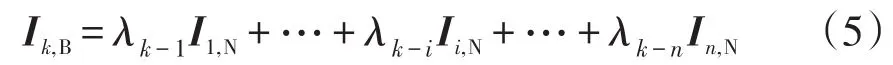
式中，λk-i为线路k电流Ik,B与节点i注入电流Ii,N的电流相关度系数。

1.1.2 功率灵敏度矩阵

电流相关度系数矩阵反映了节点注入电流与线路电流之间的关系，为得到线路功率与节点注入功率之间的关系，对式（5）进行处理可得

式中：Uk,B为线路k的首端电压相量；Ui,N为节点i的电压相量。将式（6）展开得

式中：Pk,B和Qk,B分别为线路k的有功功率和无功功率；Uk,B和φk,B分别为线路k首端电压模值和相角；Ui,N和φi,N分别为节点i电压模值和相角。

将式（7）展开，得到实数部分为

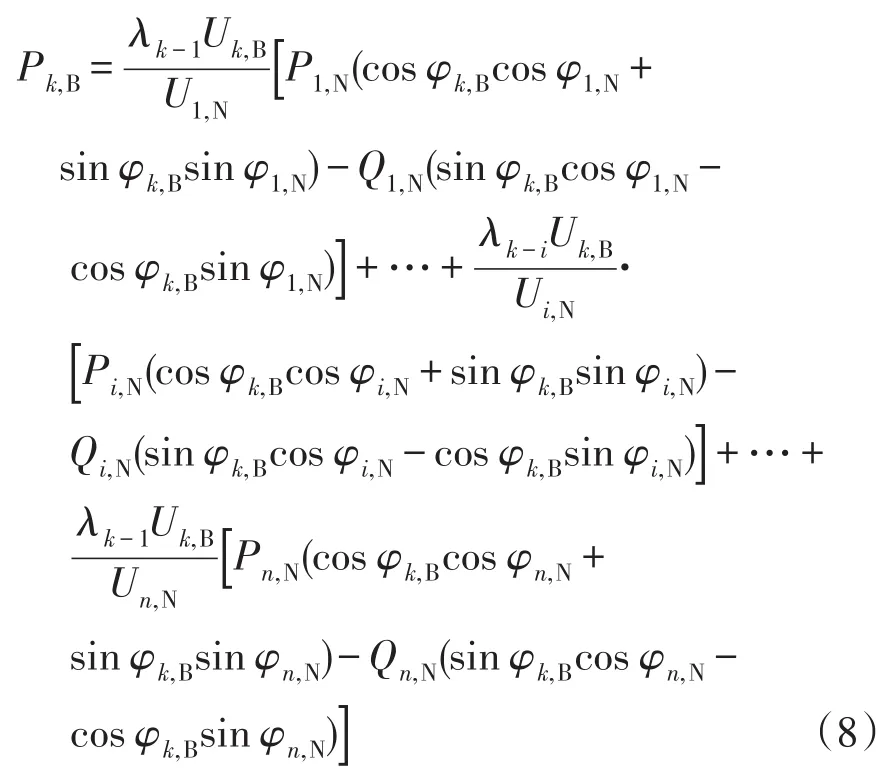
为了得到节点注入功率变化时线路功率的变化情况，将式（8）中线路有功功率和节点注入有功功率取变量形式，并将节点注入无功功率取0，可得

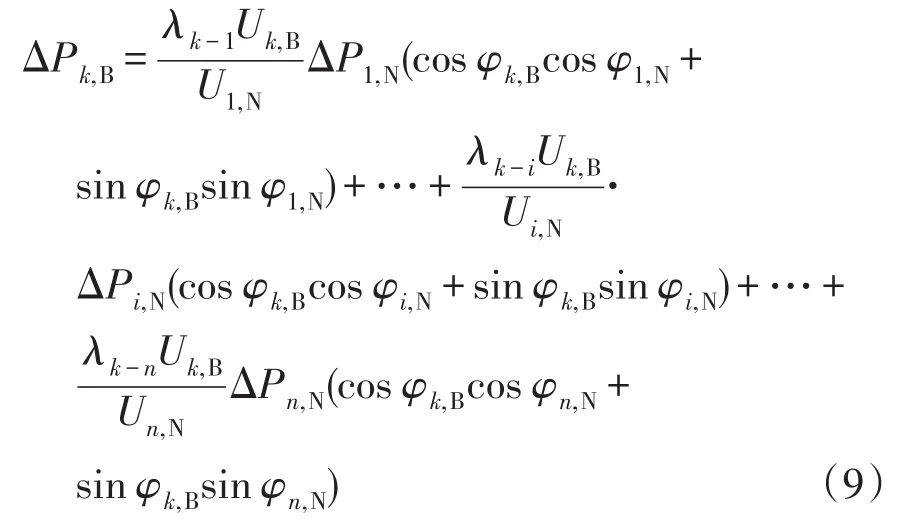
定义矩阵D（β）为线路功率变量与节点注入功率变量之间的功率灵敏度矩阵，其中线路k功率变量与节点i注入功率变量之间的功率灵敏度βk-i为

功率灵敏度矩阵结合网络拓扑参数和实际电网运行情况衡量节点注入功率对线路功率的影响。

1.2 改进节点电气介数

电网中节点可分为发电、负荷和联络节点3类[5]。节点在负荷供电以及功率传输中的重要性不仅与该节点的类型有关，还与该节点所连线路的重要性有关[2]。

在功率灵敏度矩阵和传统电气介数[9]的基础上，定义线路k的改进线路电气介数Bk为

式中：βk-（m-n）为当发电机节点m增加单位出力，负荷节点n增加单位负荷时，线路k增加的功率；Wm为发电机节点m的权重，取该发电机的实际出力；Wn为负荷节点n的权重，取该节点实际负荷；D和J分别为所有发电机节点和负荷节点的集合；Pk为线路k的当前传输功率；Pk，max为线路k的最大传输功率。

对于联络节点i，定义其改进节点电气介数Ci为

式中：F（i）为与节点i直接相连的节点集合；B（i，j）为线路lij的改进线路电气介数。

对于发电机或负荷节点i，增加一个虚拟节点h，将节点i转换为联络节点[12]，如图1所示。

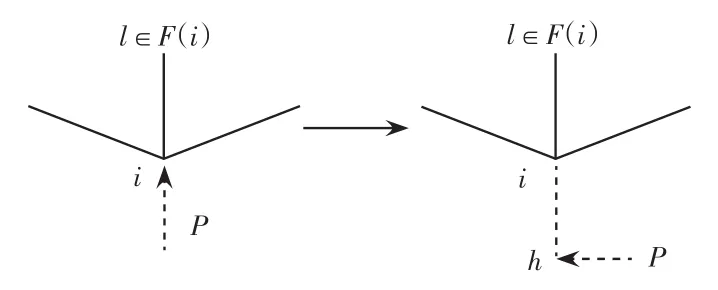
图1 虚拟节点示意Fig.1 Schematic of virtual node

当节点i为发电机节点时，在节点i和任意负荷节点n之间注入单位有功功率，线路i-h上的有功功率都为1，而其他发电机节点与任意负荷之间传输的功率都不会通过线路i-h，因此利用式（11）计算线路i-h的改进电气介数为

定义发电机节点i的改进节点电气介数为

同理，当节点i为负荷节点时，定义其改进节点电气介数为

需要说明的是，式（14）～式（16）中，为强调发电机节点和负荷节点在电网供电中的重要性，在计算线路i-h的改进线路电气介数时，认为线路i-h的负载率为1。

改进节点电气介数可有效反映节点在负荷供电和功率传输中发挥的作用，对该介数指标分析如下。

（1）改进节点电气介数定义式中，用功率代替传统电气介数[7]中的电流，能够更加直观地反映节点在电网负荷供电和功率传输中的作用。

（2）利用功率灵敏度计算改进节点电气介数，不需要进行复杂的潮流追踪运算[6]，方法简洁，计算量少，且克服了以往电气介数模型假设母线间潮流沿最短路径流动的不足。同时考虑了潮流的方向性，将不同方向的潮流进行抵消，更加真实地反映电网功率传输情况。

（3）线路功率越接近其最大传输功率，运行安全性越小，故障概率越大[13-14]，将节点所连线路负载率参与到改进节点电气介数计算中，可以更好地辨识在电网功率传输中有重要作用的关键节点。

2 节点重要性指标

2.1 负荷损失量

为负荷供电是电网的本质功能，利用移除节点i导致的系统负荷损失量可以衡量节点在电网负荷供电中的作用。

有以下两点需要说明：

（1）在移除节点i的同时，与节点i直接相连的线路也要移除；

（2）为衡量在当前电网运行情况下节点移除对负荷损失的影响，不考虑发电机再出力。

2.2 加权潮流分布熵

熵函数可作为系统分布状态的混乱性和无序性的度量[15]。系统的混乱程度越高，状态越无序，系统熵值越大；反之系统熵值越小。

文献[6]利用节点注入功率变化时的电网潮流熵判断节点的关键性；文献[15]利用节点单位负荷扰动下的潮流增量分布熵确定关键节点。以上两种方法都没有考虑线路最大传输功率及线路负载率分布情况，无法准确衡量电网潮流运行安全水平。文献[16]利用潮流分布熵衡量系统中线路负载率的分布情况，但是潮流分布熵较大可能是由于部分线路负载率偏低或部分线路负载率偏高导致，而后者的运行安全水平更低，利用该模型无法区分这两种情况。文献[17]将区间平均负载率作为权值计算，加权潮流分布熵反映系统中线路负载率的不均衡性，能有效反映系统中部分线路负载率偏高导致的潮流分布不均衡。本文利用节点受到单位注入功率扰动时的系统加权潮流分布熵反映节点在功率传输中的重要性。

假设当系统中节点i增加单位负荷，发电机节点j增加单位出力时，线路l的负载率μl为

式中：Pl为线路l的功率；Pl，max为线路l的最大传输功率。

对于正常线路，给定常数序列E=[0，e，2e，…，ne]，其中ne=1，本文取e=10%。设电网线路总数为N，用Nm表示负载率属于[me，（m+1）e）的线路条数，则线路处于[me，（m+1）e）区间的概率p（m）为

定义加权潮流分布熵为

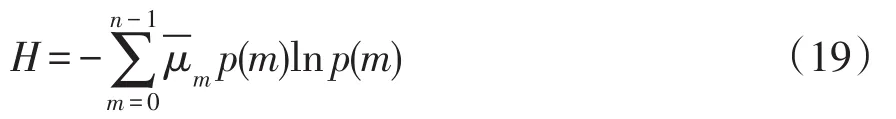
式中，μms为负载率[me，（m+1）e）区间中第s条线路的负载率。

H越大，则系统中线路负载率越不均衡，部分线路负载率过高，甚至出现过载线路，系统潮流分布的安全水平低；H越小，则系统中线路负载率处于相近区间中，系统潮流分布的安全水平较高。

需要说明的是，当节点i增加单位负荷，在选择相应的发电机节点加出力时，遵循的原则是选择节点i所属的广义潮流转移区域中距离节点i最近的发电机节点j增加单位出力。

因为根据电网拓扑结构，电力系统可抽象成一个无向图G（V，L），V表示节点集合，L表示线路集合。无向图中，如果任意两点之间都存在路径，该无向图称为连通图[18]。连通无向图中，如果去掉1个节点及与该节点相关联的边，图不再连通，称该节点为图的割点。可分图是由有限个割点连接起来的各个块组成，图中任何1条回路不可能跨越2个或2个以上的块，即构成1条回路的所有线路一定在同一块中[19]，连通图中的块对应电网中的潮流转移区域。图2中点2和点4是割点，其把电网G分为3个潮流转移区域，各区域包含的节点分别是{1，2}、{2，3，4}和{4，5，6}。

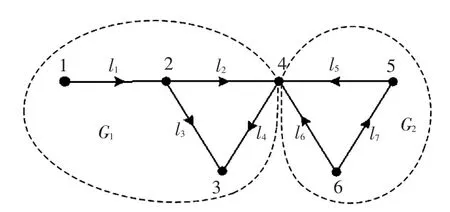
图2 广义潮流转移区域示意Fig.2 Schematic of generalized power flow transferring zone

根据潮流转移区域的定义可知，处于同一潮流转移区域中的线路可相互构成回路，为了更好地匹配电网实际情况，从供电安全性与可靠性的角度出发，当系统中节点i增加单位负荷时，选择与节点i处于同一个潮流转移区域中的距离最近的发电机节点j增加单位出力。由于实际电网中发电机节点大多属于系统边缘节点，为方便计算，需要对潮流转移区域进行扩展得到广义潮流转移区域，扩展原则如下：

（1）若某节点为邻接节点数是1的发电机或负荷节点，则将该节点归入其邻接节点所属的广义潮流转移区域中；

（2）若某线路断开会导致系统解列为两部分，且这两部分均不是发电机—母线系统，则将这两部分归为不同的广义潮流转移区域。

因此，图2所示的电网结构包括两个广义潮流转移区域，分别是G1和G2，各区域包含的节点分别是{1，2，3，4}和{4，5，6}。因此，当节点i增加单位负荷时，若节点i不是割点，则选择节点i所属的广义潮流转移区域中距离节点i最近的发电机节点j增加单位出力；若节点i是割点，则选择与节点i相连的广义潮流转移区域中距离节点i最近的发电机节点j增加单位出力。本文利用深度优先搜索方法搜索割点和块来确定广义潮流转移区域，该算法已十分成熟，本文不再赘述。

2.3 节点重要性指标

为消除负荷损失量和加权潮流分布熵之间不同量纲的影响，分别对其进行归一化处理[2]，归一化公式为

综合考虑节点移除时造成的负荷损失和节点注入功率变化时系统的线路负载率分布，定义节点重要性指标为

3 仿真算例

在IEEE39节点系统中对本文方法进行验证，该系统有4个广义潮流转移区域，分别是G1、G2、G3、G4，如图3所示。本文重点是识别电网负荷供电和功率传输中的关键节点，发电机节点是为电网提供电能的重要节点，本文不再对发电机节点进行分析。

图3 IEEE39节点系统Fig.3 IEEE 39-node system

利用式（14）～式（16）计算电网各节点的改进节点电气介数，并按照从大到小的顺序对节点进行排序，排序前17位的节点如表1所示。

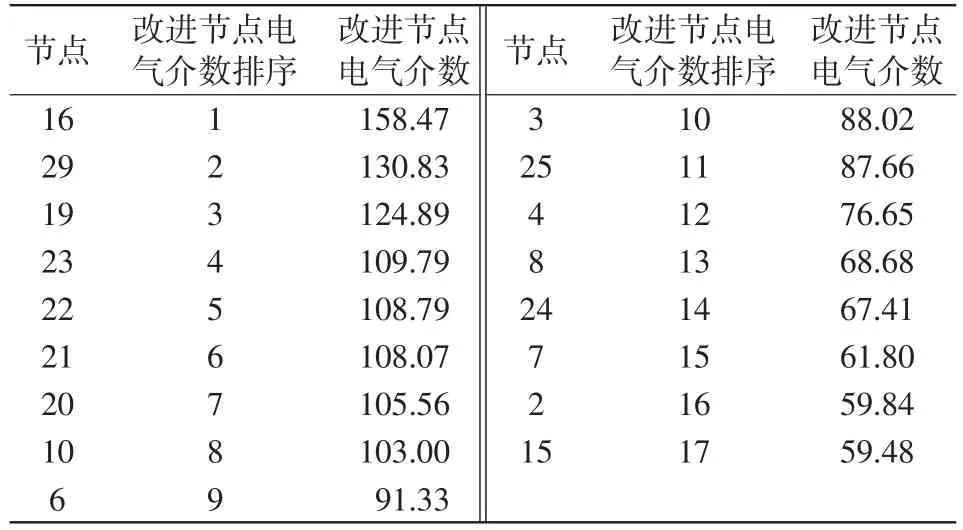
表1 基于改进电气介数的关键节点辨识结果Tab.1 Identification results of key nodes based on improved node electric betweenness

计算电网各节点移除后的负荷损失量及其受到单位负荷冲击时的加权潮流分布熵，得到各节点的重要性指标。将本文方法所识别的关键节点结果与文献[7-8]进行对比，如表2所示。

表2 关键节点辨识结果对比Tab.2 Comparison among key node identification results

仿真分析结果如下。

（1）观察表1和表2，利用本文方法和文献[7-8]方法识别的前17位关键节点中，分别有15和10个节点在重要性指标排序中位于前17位，并且本文方法识别的关键节点的改进节点电气介数排序与其相应的重要性指标排序更加接近。这说明利用改进节点电气介数可以有效识别电网负荷供电和功率传输中的关键节点，证明了本文方法的正确性和优越性。

（2）利用功率灵敏度计算改进节点电气介数，计算过程简单，不需要进行复杂的潮流追踪[6]，克服了以往方法假设节点间功率按最短路径传输[5]的不足，以及传统节点电气介数没有考虑线路中潮流方向性[7]的缺点。

（3）移除节点导致的负荷损失量不仅与该节点本身所带负荷量有关，还与该节点在电网中所处位置有关。例如节点22本身并不带负荷，但是移除节点22会直接导致发电机节点35退出运行，因此移除节点22时会导致系统损失负荷6.5 MW。

（4）综合考虑节点移除造成的负荷损失和节点受到注入功率扰动时的加权潮流分布熵制定重要性指标，可有效衡量节点在电网负荷供电和功率传输中的作用，验证关键节点识别结果的正确性。

4 结论

本文提出一种基于改进节点电气介数的电网关键节点辨识方法。该方法的主要优点有：

（1）结合节点类型的不同，利用功率灵敏度矩阵计算改进节点电气介数识别电网的关键节点，计算过程简单，避免了复杂的潮流追踪运算，克服了以往方法假设节点间功率按最短路径传输的不足，以及传统节点电气介数没有考虑线路中潮流方向性的缺点；

（2）综合考虑节点移除造成的负荷损失和节点受到功率扰动时的加权潮流分布熵，定义节点重要性指标衡量节点在电网负荷供电和功率传输中的作用，对关键节点识别结果进行检验。

本文方法虽有一定的有效性，但只重点考虑了节点在电网负荷供电和功率传输中的作用，未考虑系统电压、无功功率及拓扑强健性等问题，如何更全面地反映节点在电网中的关键性是下一步的研究方向。

[1]张华一，张晶晶（Zhang Huayi，Zhang Jingjing）.基于脆性风险熵的电力系统连锁故障预测（Brittle risk entro⁃py based model for forcasting power system cascading fail⁃ures）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2015，27（4）：39-43.

[2]雷成，刘俊勇，魏震波，等（Lei Cheng，Liu Junyong，Wei Zhenbo，et al）.计及网络传导能力与抗干扰能力的节点综合脆弱评估模型（Integrative evaluation model of node vulnerability considering network transmission ability and anti-interference ability）[J].电力自动化设备（Electric Power Automation Equipment），2014，34（7）：144-149，156.

[3]陈晓刚，孙可，曹一家（Chen Xiaogang，Sun Ke，Cao Yijia）.基于复杂网络理论的大电网结构脆弱性分析（Structural vulnerability analysis of large power grid based on complex network theory）[J].电工技术学报（Transactions of China Electrotechnical Society），2007，22（10）：138-144.

[4]苏慧玲，李扬（Su Huiling，Li Yang）.从电力系统复杂网络特征探讨元件的脆弱性（Electrical component vulner⁃ability analysis from complex network characteristics of power systems）[J].电力系统自动化（Automation of Elec⁃tric Power Systems），2012，36（23）：12-17，77.

[5]丁明，韩平平（Ding Ming，Han Pingping）.加权拓扑模型下的小世界电网脆弱性评估（Vulnerability assessment to small-world power grid based on weighted topological model）[J].中国电机工程学报（Proceedings of the CSEE），2008，28（10）：20-25.

[6]王涛，高成彬，顾雪平，等（Wang Tao，Gao Chengbin，Gu Xueping，et al）.基于功率介数的电网关键环节辨识（Power betweenness based identification of power grid critical links）[J].电网技术（Power System Technology），2014，38（7）：1907-1913.

[7]徐林，王秀丽，王锡凡（Xu Lin，Wang Xiuli，Wang Xi⁃fan）.基于电气介数的电网连锁故障传播机制与积极防御（Cascading failure mechanism in power grid based on electric betweenness and active defence）[J].中国电机工程学报（Proceedings of the CSEE），2010，30（13）：61-68.

[8]董光德（Dong Guangde）.基于潮流介数和UPFC的小世界电网连锁故障模型研究（Research on Cascading Fail⁃ures Model in Small World Grid Based on Power Flow Be⁃tweenness and UPFC）[D].重庆：重庆大学电气工程学院（Chongqing：School of Electrical Engineering，Chongqing University），2013.

[9]徐林，王秀丽，王锡凡（Xu Lin，Wang Xiuli，Wang Xi⁃fan）.电气介数及其在电力系统关键线路识别中的应用（Electric betweenness and its application in vulnerable line identification in power system）[J].中国电机工程学报（Proceedings of the CSEE），2010，30（1）：33-39.

[10]沈瑞寒，刘涤尘，赵洁，等（Shen Ruihan，Liu Dichen，Zhao Jie，et al）.基于加权网络模型的电网潮流转移下危险线路识别（Weighted network model based recognition of dangerous lines under power flow transferring）[J].电网技术（Power System Technology），2012，36（5）：245-250.

[11]徐慧明，毕天姝，黄少锋，等（Xu Huiming，Bi Tianshu，Huang Shaofeng，et al）.基于广域同步测量系统的预防连锁跳闸控制策略（Study on wide area measurement system based control strategy to prevent cascading trips）[J].中国电机工程学报（Proceedings of the CSEE），2007，27（19）：32-38.

[12]王凯（Wang Kai）.基于复杂网络理论的电网结构复杂性和脆弱性研究（Research on Structural Complexity and Vulnerability of Power Grids Based on Complex Network Theory）[D].武汉：华中科技大学电气与电子工程学院（Wuhan：College of Electrical and Electronic Engineer⁃ing，Huazhong University of Science and Technology），2011.

[13]钟贵和，王星华，甘德树，等（Zhong Guihe，Wang Xing⁃hua，Gan Deshu，et al）.输电断面的有功安全预防-校正负荷调整算法（Load adjusted algorithm on active power prevention-correction of transmission section）[J].电力系统保护与控制（Power System Protection and Control），2014，42（16）：15-20.

[14]雷雪姣，潘士娟，管晓宏，等（Lei Xuejiao，Pan Shijuan，Guan Xiaohong，et al）.考虑传输安全裕度的电力系统发电经济调度（Transmission safety margin constrained unit commitment in power systems）[J].中国电机工程学报（Proceedings of the CSEE），2014，34（31）：5651-5658.

[15]李勇，刘俊勇，刘晓宇，等（Li Yong，Liu Junyong，Liu Xiaoyu，et al）.基于潮流熵的电网连锁故障传播元件的脆弱性评估（Vulnerability assessment in power grid cas⁃cading failures based on entropy of power flow）[J].电力系统自动化（Automation of Electric Power Systems），2012，36（19）：11-16.

[16]曹一家，王光增，曹丽华，等（Cao Yijia，Wang Guangzeng，Cao Lihua，et al）.基于潮流熵的复杂电网自组织临界态判断模型（An identification model for self-orga⁃nized criticality of power grids based on power flow entro⁃py）[J].电力系统自动化（Automation of Electric Power Systems），2011，35（7）：1-6.

[17]刘文颖，但扬清，朱艳伟，等（Liu Wenying，Dan Yangqing，Zhu Yanwei，et al）.复杂电网自组织临界态辨识物理指标研究（Research on physical indicators to identi⁃fy power system self-organized critical state）[J].电工技术学报（Transactions of China Electrotechnical Society），2014，29（8）：274-280，288.

[18]郭志忠.电力网络解析论[M].北京：科学出版社，2008.

[19]苗世洪，马帅，尚亚男，等（Miao Shihong，Ma Shuai，Shang Yanan，et al）.基于割点和路径搜索的输电断面快速识别方法（A fast recognition method of transmission section based on cut-vertex and path search）[J].电力系统自动化（Automation of Electric Power Systems），2014，38（2）：39-45.

关于参考文献著录格式

1 连续出版物

标引项顺序号 作者．题名．刊名（外文刊名可缩写，缩写后的首字母应大写，并省略缩写点“．”），出版年份，卷号（期号）：起始或起止页码

2 专著

标引项顺序号 作者．书名．版本（第1版不标注）．出版地：出版者，出版年.（专著中的析出文献应注明起止页码）

3 论文集

标引项顺序号 作者．题名．见（英文时用In）：主编.论文集名．出版地：出版者，出版年．起止页码

4 学位论文

标引项顺序号 作者．题名：［学位论文］．保存地点：保存单位，年份

5 专利

标引项顺序号 专利申请者．题名．国别，专利文献种类，专利号．出版日期

6 技术标准

标引项顺序号 起草责任者．标准代号 标准顺序号—发布年 标准名称．出版地：出版者，出版年（也可略去起草责任者、出版地、出版者和出版年）

摘编于《中国高等学校自然科学学报编排规范》（修订版）

Identification of Key Nodes in Power Grid Based on Improved Node Electric Betweenness

XU Yan，ZHI Jing
（State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources，North China Electric Power University，Baoding 071000，China）

TM711

A

1003-8930（2017）09-0107-07

10.3969/j.issn.1003-8930.2017.09.018

2015-05-21；

2016-11-01

徐 岩（1976—），男，博士，副教授，研究方向为电力系统保护与安全控制、新能源发电和智能电网。Email：xy19761001@aliyun.com

郅 静（1990—），女，硕士研究生，研究方向为电力系统保护与安全控制。Email：zj1217@139.com