基于人工神经网络的天然气井产量计算方法研究

宋尚飞，洪炳沅，史博会*，吴海浩，康琦，王智，宫敬*

1 中国石油大学(北京)油气管道输送安全国家工程实验室/石油工程教育部重点实验室/城市油气输配技术北京市重点实验室，北京102249

2 西安长庆科技工程有限责任公司，西安 710000

基于人工神经网络的天然气井产量计算方法研究

宋尚飞1，洪炳沅1，史博会1*，吴海浩1，康琦1，王智2，宫敬1*

1 中国石油大学(北京)油气管道输送安全国家工程实验室/石油工程教育部重点实验室/城市油气输配技术北京市重点实验室，北京102249

2 西安长庆科技工程有限责任公司，西安 710000

随着石油行业不断向海洋发展，水下油气生产工艺也随之诞生，传统的技术手段面临诸多新的问题。虚拟计量系统已经逐步在国内外的海上油气田生产系统中开始应用。该技术利用油气田的常规基础工艺参数以及从生产控制系统获取的实时仪表数据，通过多种模型实时计算出单井油气水各相的流量。本文主要研究人工神经网络在虚拟计量方面的应用。由于目前常用的井筒模型不能适应产量的瞬时变化，不能及时准确地预测产量，本文引入具有高度非线性预测能力的误差反向传播的人工神经网络方法，以人工调试后的井筒模型结果作为数据样本库，模拟各种影响因素与天然气井产量之间的映射关系，通过学习和训练建立了基于BP神经网络模型的天然气井产量计算模型。预测结果表明：该方法的计算结果与现场物理流量计测量值的相对误差平均值为3.33%，超过80%的数据点相对误差处于±5%内，预测精度较高。综合分析表明，人工神经网络模型能够满足实际生产需要，且该模型结构简单，不拘泥于具体的形式，计算量少。

水下油气生产工艺；虚拟计量系统；人工神经网络模型；天然气—凝析液管道；深海流动安全保障

0 前言

VMS(Virtual Metering System) 技术早在20世纪90年代就被提出并首先应用于油气田开发中[1]。VMS技术经过20多年的发展，不仅被应用于海上油气田的开发中，还与目前广泛使用的流动安全保障及管道管理系统有机结合[2]，成为海上油气开发与运营管理中非常重要的先进技术。VMS技术具有高度的集成性，为作业者提供了极大方便，在性价比方面也有很大优势，还可与实时的流动管理系统相结合。在水下油气田的开发中可以部分代替传统多相计量设备，也可作为实体流量计的补充或备用方案[3]。

国外有关技术公司已经开发出了多种适用于深水油气田流动安全保障在线监测与管理系统，并在北海、墨西哥湾及西非等地区的一些深水油气田上得到成功应用，取得了良好的结果。如FMC旗下的FAS系统，提供了在线流动安全保障的一揽子解决方案，包括了虚拟计量、海底管道动态监测、乙二醇注入量控制、油嘴开度优化及地层水监测5个模块。SPT公司为中国南海的崖城气田提供了包括虚拟计量及段塞流跟踪在内的OLGA online系统，另外还有BP的ISIS系统、TOTAL的WPM系统[4]等。一些国际大型石油公司(例如Chevron、Shell、TOTAL等)已将流动安全保障在线监测与管理系统列为其新油气田开发的标准设计，并在已有油气田上推广使用[5]。我国目前在该方面的研究才刚刚开始，本研究组依托多相流模拟技术，自行研发了流动监测与管理系统。2014年1月，该系统已经在中国南海某气田区块成功投入使用。经过近4年的运行，结果证明自研的VMS 系统整体平稳运行，硬件设备未出现故障。对比显示，VMS所算出的单井流量和总流量与平台上流量计的总体测量结果吻合较好，满足工程实际正常生产的精度要求，创造了可观的经济效益和价值[6-9]。

人工神经网络(Arti fi cial Neutral Networks)是一种类似于人类神经系统的信息处理技术[10]，可以视为一种功能强大、应用广泛的机器学习算法，在解决事物的模糊关系及非线性预测方面具有很强的智能化。通过建立合理的神经网络对系统的输入输出样本进行训练和学习，能够在适当精度内逼近任意复杂的非线性系统。这一优良性能使得人工神经网络成为多维非线性函数的通用数学模型[11]。近年来，人工神经网络理论的发展，特别是误差反向传播算法(BP 算法)的出现，使得人工神经网络成为一种分析预测非线性复杂体系性能的有效方法。目前，人工神经网络已被广泛应用于模式识别、信号处理、优化计算、参数匹配及预测、参数空间分布预测等研究领域。近年来，人工神经网络技术已被引入石油行业，能很好地解决生产过程中的非线性问题，应用范围较广[10]，已在储层参数预测、钻井井下复杂情况及事故诊断、预测、储层裂缝识别、气井管理及动态预测等领域内取得了良好的应用效果，理论发展也在不断完善。

水下油气生产工艺系统是一个涉及多学科、多作业环节的庞大的地下隐藏工程。在天然气井生产过程中，存在着大量且复杂的不确定性因素，都会对天然气井的生产产生影响。目前，国内外学者对虚拟计量技术进行了广泛而深入的研究，建立了多种数学模型。但这些模型都是通过气体管流连续性方程、运动方程、能量方程等基本方程推导出来的，同时，公式也存在一定的假设条件，比如气体压缩因子为常数、不考虑液体压缩性、忽略流动过程中摩擦等等，不符合实际生产情况。因此，这些模型的应用均具有一定的局限性，也会产生相应的不可避免的系统误差。

人工神经网络所拥有的可逼近任意非线性函数的优点非常适用于天然气井产量的预测研究，因此本文针对人工神经网络展开了一系列研究。具体研究思路是：首先，根据前人的研究成果，寻求与天然气井流量关联度较大的相关因素；然后，根据网络的要求，确定网络的结构，同时选取相应的算法；最后建立基于人工神经网络模型的天然气井产量计算方法，将人工神经网络引入虚拟计量这一新兴技术中。

1 VMS应用简介

1.1 VMS系统简介

根据在线流动安全保障系统的基本概念，我们课题组开发了海上凝析气田流动监测系统，这是一套以油气田的实时生产数据为依据的可用于反映生产流动过程的计算分析系统，可用于水下气井井口流量测量及海底管道流动在线模拟。其中包括基于井筒模型和油嘴模型的虚拟计量系统(VMS)，该系统已在我国南海某凝析气田投入使用。该系统具有以下功能：

(1) 基础数据及主要功能

为完成实时井口流量的计算，VMS需要的参数分为3部分：流体基础参数、流动系统基础参数、实时生产数据。流体基础参数主要指天然气的组分数据。流动系统基础参数指气藏IPR数据、井筒的轨迹和结构、地层温度分布、油嘴开度与Cv值的对应关系、海底管道参数等。另外就是从DCS（分布式控制系统，Distributed Control System）获取的实时生产数据，这些数据包括：井筒底部的压力及温度、井口压力及温度、油嘴后压力及温度、油嘴的开度、采油树阀门状态等。

通过VMS的分析计算，可以实时获得的数据包括：单井的总质量流量，气、油、水三相的体积流量(标况)，以及气田生产井的总流量。另外还可提供各个生产井的时、日、周、月时间范围的流量累积值。

(2) VMS系统构架

VMS系统主要由软件系统和硬件系统两部分构成。其中硬件系统主要承担与现场DCS的数据通信，并作为VMS的运行平台；软件系统是VMS的核心，包括数据库、组态软件及核心计算软件等部分。VMS的系统结构和基本工作原理参见图 1。

VMS的软件部分主要包括组态软件、数据库软件及核心计算软件。核心计算软件包括所有流量算法及数据处理过程，为适应同时计量多口生产井的要求，采用了多线程的程序开发技术。核心计算模块采用了多模型同时计算的方式，所以即使个别井的井底或井口喷嘴前、后压力和温度传感器失效，系统依然能够正常工作。

硬件系统主要包括1台VMS服务器，2套冗余配置的通信服务器和交换机。在这个设计方案中，系统所需的硬件设备只是用于获取实时生产数据的通用数字通信设备，而不需要对原有生产工艺流程及DCS做任何改动。获取实时生产数据的方式是被动单向的，因此不会对生产系统产生任何干扰。

(3) 物理模型和计算方法

图2为一个典型的水下气田流动系统示意图。根据节点分析原理，从井底至采油平台的流动存在3种流动形式即地层中的渗流、井筒及海管中的多相流动及过油嘴的多相流动。海上凝析气田流动监测系统就是根据这3种流动的特点及形式，建立相应的模型及算法[12-13]，实现虚拟计量。目前系统中采用的井筒模型，从2014年1月至今正常运行，积累了大量生产数据。

1.2 现场区块应用

我国南海某盆地的实际生产区块A有两个气井：井A1和井A2，均属边际气田，开发方式为采用水下生产系统进行开发。平台上装有段塞捕集器及分相流量计对两口井总产量进行计量，同时选择VMS系统对该区块进行分相计量。模拟因果变量之间的内在关系，所以其非线性映射功能应用十分广泛，几乎涉及所有领域。在现实生活中，许多系统的输入和输出之间存在着非常复杂的非线性关系，对于这类系统，往往很难用传统的数理方法建立起数学模型。通过建立合理的神经网络对系统的输入输出样本进行训练和学习，能够在适当精度内逼近任意复杂的非线性系统。这一优良性能使得人工神经网络成为多维非线性函数的通用数学模型。该模型的

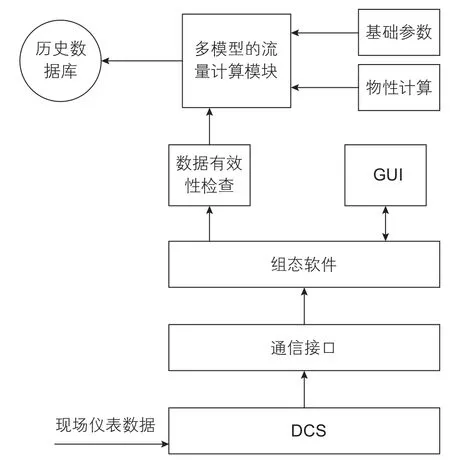
图1 VMS系统的基本构成Fig. 1 Basic architecture of VMS

2 BP人工神经网络建模

由于人工神经网络模型属于隐式模型，具有自组织、自适应性以及学习功能，在理论上能够逼近任意非连续映射，能够在各种不确定因素的影响下较好地表达是非解析的，输入输出数据之间的映射规则由神经网络在学习阶段自动抽取并分布式存储在网络的所有连接中。

图2 水下凝析气田生产系统示意图Fig. 2 Subsea gas production system diagram

网络拓扑结构确定的是否合理，直接影响到人工神经网络模型结果的适用性和精确性，因此网络拓扑结构的确定是建立BP人工神经网络模型的重点工作。网络拓扑结构的确定包括网络层数、输入层神经元数、隐含层数、隐含层神经元数、输出层神经元数等几个方面。

本文运用MATLAB语言中的神经网络工具箱对模型进行求解。神经网络工具箱是以神经网络理论为基础，用MATLAB语言构造出典型神经网络的传递函数，如 S 型、线性等传递函数，使设计者对所选网络输出的计算，变成对传递函数的调用。另外，根据各种典型的修正网络权值规则，加上网络的训练过程，用MATLAB编写出各种网络设计与训练的子程序，网络的设计者则可以根据自己的需要去调用工具箱中有关神经网络的设计训练程序，使自己从繁琐的编程中解脱出来，提高开发效率，减少工作量，节省大量时间。运用MATLAB神经网络工具箱求解BP模型的关键是传递函数和训练函数的选择，不同的函数可以取得不同的预测效果。

2.1 网络层数和输入输出层节点数的确定

在BP人工神经网络拓扑结构中，输入层与输出层是必备的，而隐含层层数是确定网络层数的关键所在。关于隐含层的层数，相关文献研究表明[14]，含有2个隐含层的BP网络更易陷入局部极小，更难以训练。因此本文建立的BP神经网络模型层数取3层，即由一个输入层，一个隐含层和一个输出层构成。

由前叙可知，在天然气井生产过程中从井底至采油平台的流动存在3种流动形式即地层中的渗流、井筒及海管中的多相流动及过油嘴的多相流动。3种流动形式都会对气井产量产生影响，同时考虑到获取数据的难易程度，确定BP神经网络的输入层应具有7个神经元，分别是井底温度、井底压力、油嘴前温度、油嘴前压力、油嘴开度、油嘴后温度、油嘴后压力。输出层仅含1个神经元，输出网络学习和预测的结果，即与输入信息相对应的天然气井瞬时产量。

2.2 隐含层神经元数的确定

对于如何选择隐含层神经元的个数，至今为止尚未找到一个很好的解析式，隐含层神经元数往往根据前人的设计经验和自己试验来确定。本文根据Kolmogorov定理[14]，先初步确定隐含层神经元数，再经过反复测试调整隐含层神经元数，最终选择隐含层的节点个数为20个。

2.3 网络传递函数的确定

BP人工神经网络的传递函数有很多种[15-16]。包括对数S型、正切S型、线性传递函数等。BP人工神经网络通常有一个或多个隐层，该层中的神经元均采用sigmoid型传递函数，输出层的神经元则采用线性传递函数，整个网络的输出可以取任意值。3种典型传递函数的输入输出特性如图3所示。

根据不同传递函数的特点，经过网络的学习和测试发现：当隐层传递函数为tansig，输出层传递函数为purelin时，网络能够在规定迭代次数内收敛，且误差较小，认为此时网络达到最佳。所以，确定隐层的传递函数为 tansig，输出层的传递函数为 purelin。

图3 三种典型传递函数的输入输出特性Fig. 3 The input and output characteristics of three kinds of typical transfer function

2.4 样本库的建立

神经网络的参数获取是建立在大量样本库数据的基础上的，只有通过大量准确的历史数据的训练和学习，才能使神经网络更逼近实际的非线性映射。

本文拟以我国南海某盆地生产区块的气井A1 和井A2的生产数据作为样本库。但是在该凝析气田现场仅有一台超声波流量计对A1井、A2井进行合并计量，不能直接得到相应的单井流量数据。目前主要用虚拟计量系统的井筒模型计算单井流量，计算结果基本可满足工程要求。但其中井筒传热系数等重要的参数需要考虑不同的工况进行校核，为建立样本库，首先应对井筒模型的参数进行人工调试与参数调整，使之与实际相吻合。本文首先根据现场实际数据对井筒模型的相关参数进行反算，得到较为准确的油气水三相单井流量值，结果如图4所示。井筒模型的结果与现场流量计结果对比误差较小，相对误差平均值为3.29%，处于可接受范围，可认为本数据库数据较为准确。

样本库的容量和准确性直接影响着神经网络模型的结果和性能，在样本库的建立过程，充分考虑海洋工程实际情况，优选油气生产过程中可能出现的不同油嘴开度、不同产量等信息，力求所建立的样本库能够涵盖实际工程所有可能出现的情况。通过对数据的筛选和选择，最终确定12 424组数据作为样本库对人工神经网络进行训练和学习。但是，样本库中数据个数不是恒定不变的，随着现场数据的进一步收集和整理，在后续研究中会不断对样本库进行修正和丰富，力求可以完整地反映该水下生产系统的信息，以供模型学习和训练，提高模型的适应性。

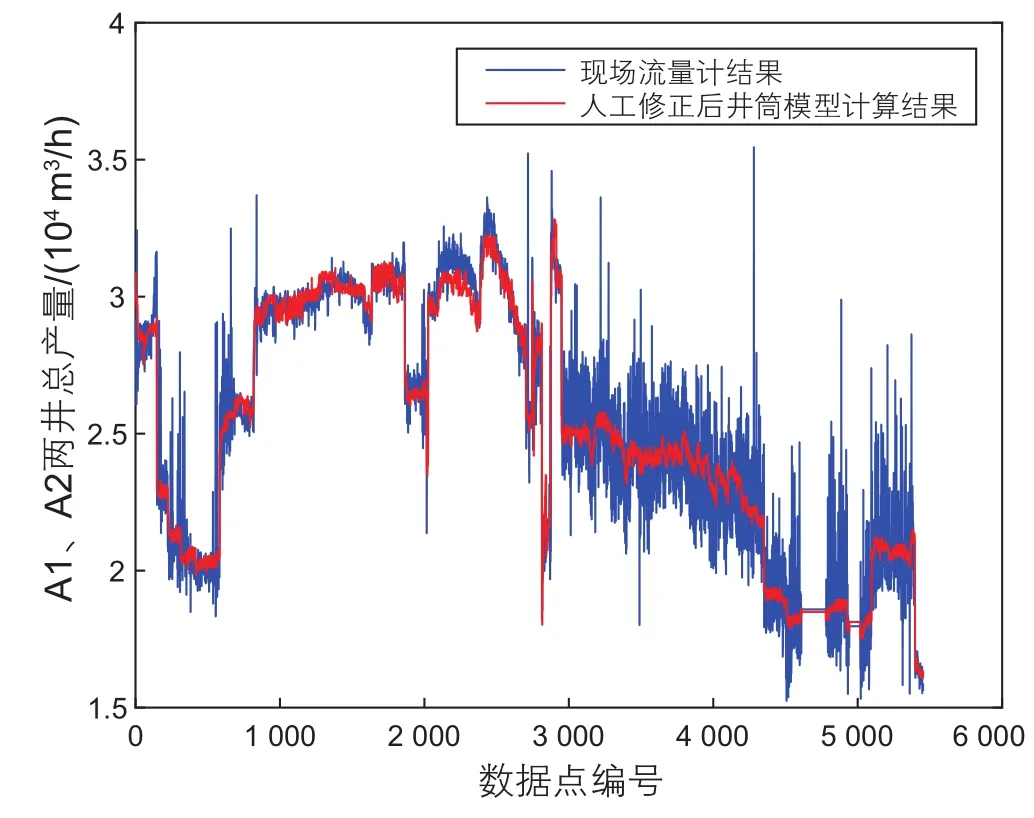
图4 人工修正后井筒模型与现场流量计结果对比Fig. 4 Compared with arti fi cial modi fi ed wellbore model and lf owmeter of A1 and A2

2.5 BP神经网络模型的求解

本文利用MATLAB神经网络工具箱建立相应的BP神经网络，如图5所示该神经网络具有7×20×1的网络结构，隐含层采用tansig传递函数，输出层采用purelin传递函数，用已建好的样本库对该网络进行学习和训练，获得相应的结构参数。

3 模型误差分析

3.1 BP神经网络模型与井筒模型对比

利用训练后的BP神经网络分别计算两井的流量。图6所示为A1单井BP神经网络模型与井筒模型计算结果的对比，可知BP神经网络模型与井筒模型计算结果的吻合度较高，相对误差绝对值平均为0.66%，只有不超过0.1%的数据点误差较大，如图7所示。相对误差服从正态分布，均值为-0.031%，标准差为0.011 0。99.74%的数据点相对误差处于±3%内，超过80%的数据点相对误差处于±1%内。

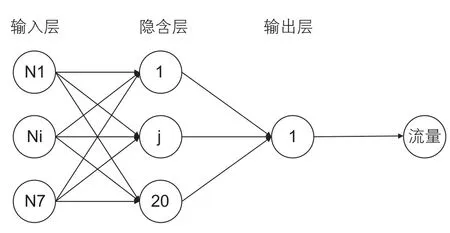
图5 BP神经网络结构示意图Fig. 5 Schematic diagram of the structure of BP neural network

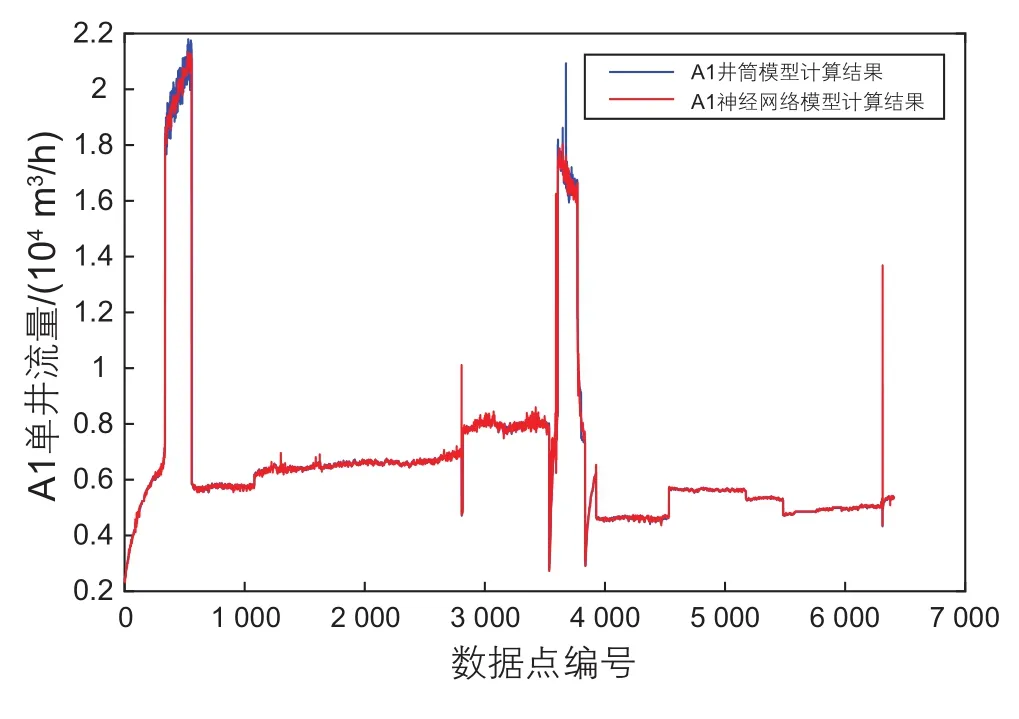
图6 A1井神经网络模型与井筒模型计算结果Fig. 6 The results of A1 by neural network model and wellbore model

图8所示为A2单井BP神经网络模型与井筒模型计算结果的对比，可知BP神经网络模型与井筒模型计算结果的吻合度较高，相对误差绝对值平均为1.14%，只有不超过0.1%的数据点误差较大，如图9所示。相对误差服从正态分布，均值为-0.052 2%，标准差为0.020 7。99.74%的数据点相对误差处于±6.0%内，超过80%的数据点相对误差处于±2%内。

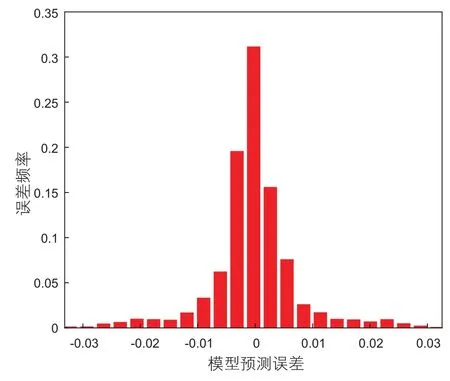
图7 A1井神经网络模型与井筒模型计算误差频率分布直方图Fig. 7 Histogram of frequency distribution of A1 calculation error by neural network model

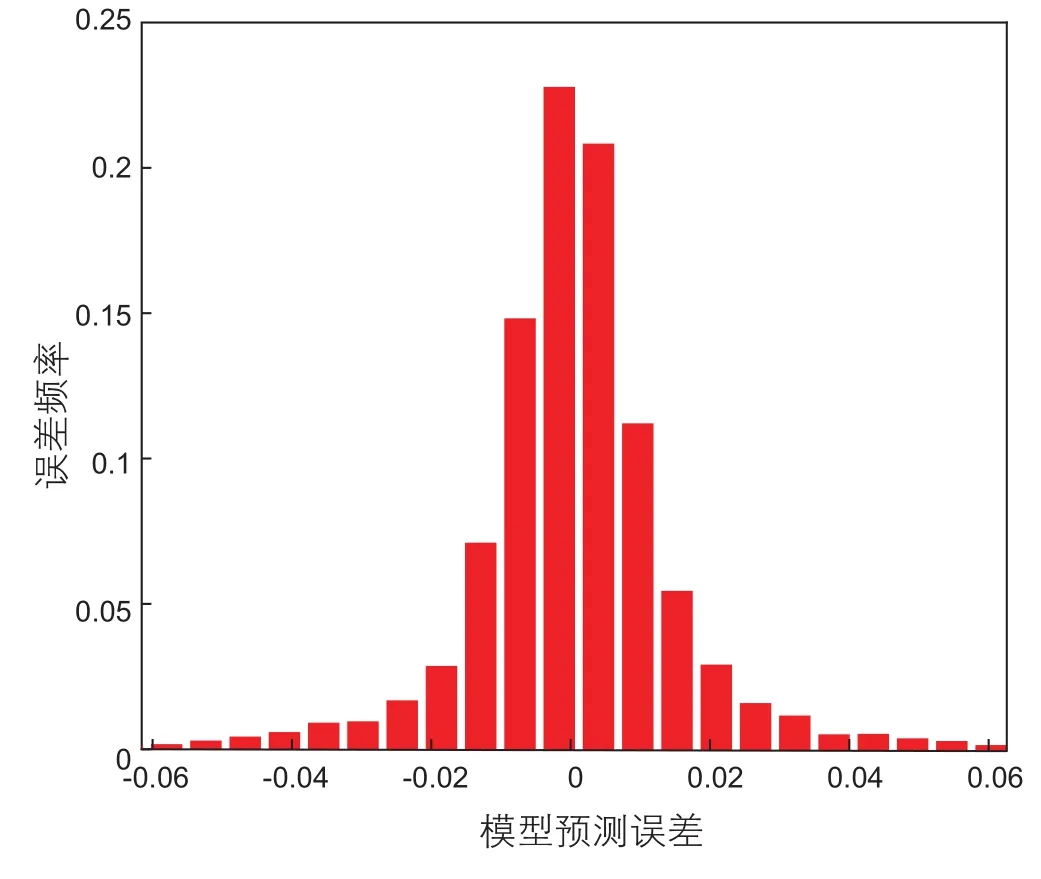
图9 A2井神经网络模型与井筒模型计算误差频率分布直方图Fig. 9 Histogram of frequency distribution of A2 calculation error by neural network model

3.2 单井生产时BP神经网络模型与现场流量计对比

图10所示为A1单井生产时BP神经网络模型与现场流量计结果的对比，BP神经网络模型与现场流量计数据结果基本吻合，相对误差绝对值平均为3.25%，只有少量的数据点误差较大。如图 11所示，相对误差服从正态分布，均值为-5.520 5×10-7，标准差为0.045 9。99.74%的数据点相对误差处于±10%内，超过80%的数据点相对误差处于±5%内。

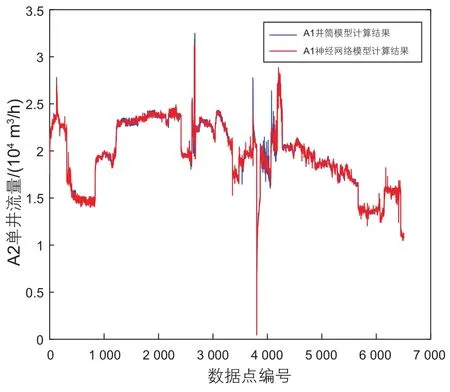
图8 A2井神经网络模型与井筒模型计算结果Fig. 8 The results of A2 by neural network model and wellbore model

图10 A1单井生产时神经网络与流量计结果对比Fig. 10 Comparison of neural network and the fl owmeter of A1

图12所示为A2单井生产时BP神经网络模型与现场流量计结果的对比，可知BP神经网络模型与现场流量计数据结果的吻合度较高，相对误差绝对值平均为4.65%，因为现场流量计数据波动性较大，有少量的数据点误差较大。如图 13所示，相对误差服从正态分布，均值为-0.18%，标准差为0.0715。99.74%的数据点相对误差处于±20%内，超过80%的数据点相对误差处于±5%内。

3.3 两井同时生产时BP神经网络模型与现场流量计对比

如图14所示为两井同时生产时BP神经网络模型与现场流量计结果的对比，可知BP神经网络模型与现场流量计数据结果的吻合度较高，相对误差绝对值平均为3.33%，因为现场流量计数据波动性较大，有少量的数据点误差较大。如图15所示，99.74%的数据点相对误差处于±15%内，超过80%的数据点相对误差处于±5%内，相对误差标准差为0.050 8。

图11 A1单井生产时BP神经网络计算结果误差频率分布直方图Fig. 11 A1 Histogram of frequency distribution of BP neural network calculation error

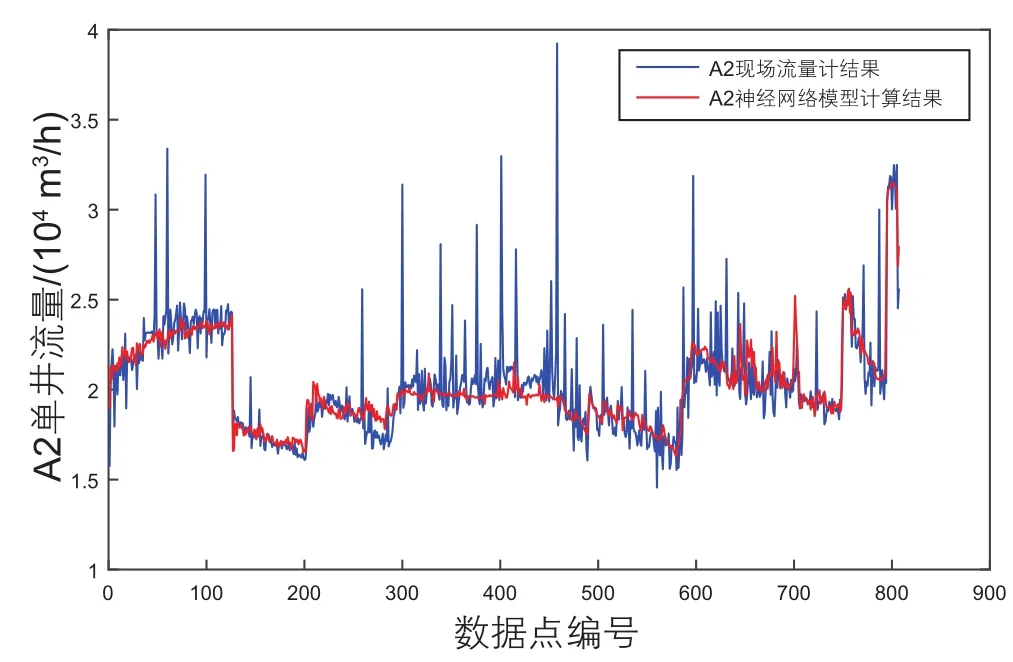
图12 A2单井生产时神经网络与流量计结果对比Fig. 12 Comparison of neural network and the fl owmeter of A2

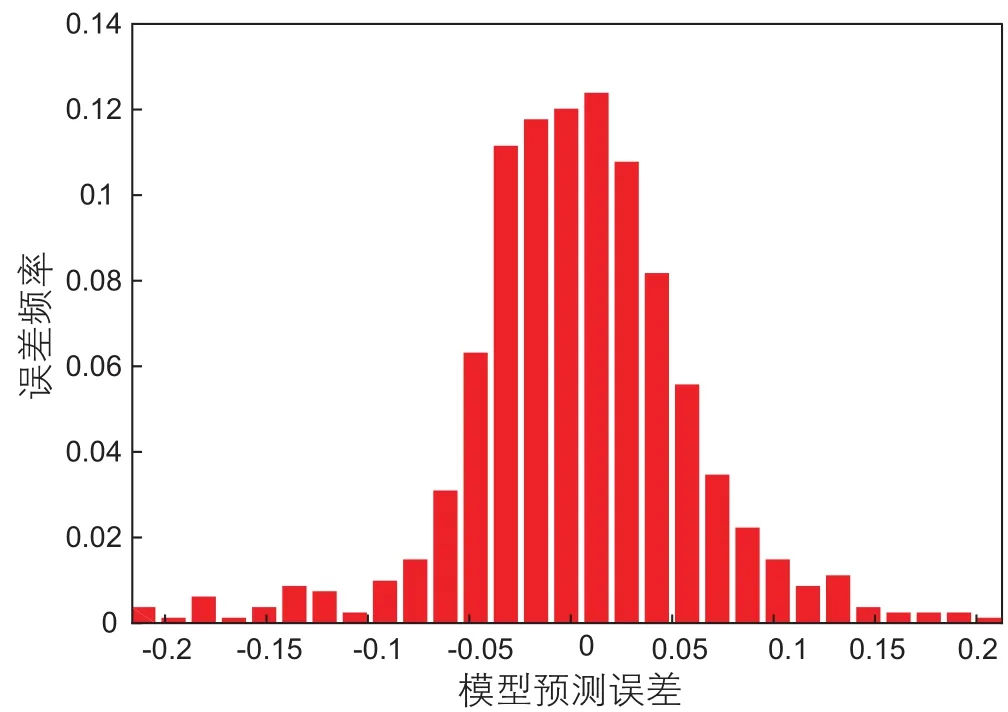
图13ｃA2单井生产时BP神经网络与流量计结果误差频率分布直方图Fig. 13 A2 Histogram of frequency distribution of BP neural network calculation error

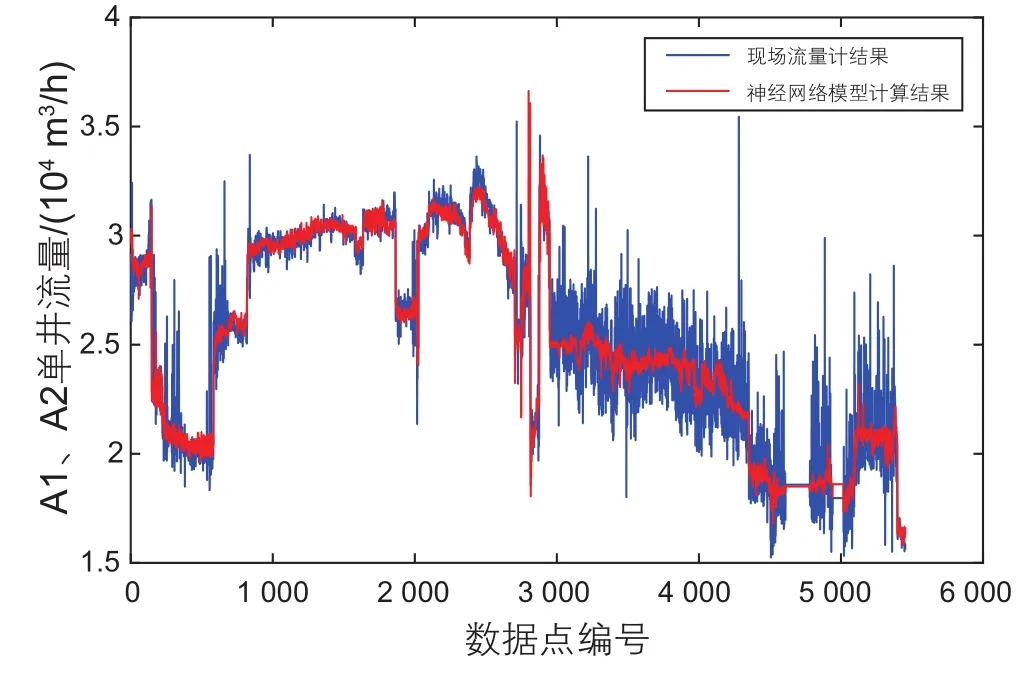
图14 两井同时生产时神经网络模型与流量计结果对比Fig. 14 Comparison of neural network and the fl owmeter of A1 and A2

图15 两井同时生产时BP神经网络与流量计结果误差频率分布直方图Fig. 15 Histogram of frequency distribution of BP neural network calculation error

4 结论

本文主要研究人工神经网络在天然气井计量方面的应用。由于目前井筒模型并不能适应产量的瞬时变化，并及时准确预测，本文以人工调试后的井筒模型结果作为数据样本库，建立了多因素影响下非线性的天然气井流量计算模型。预测结果表明，该方法的计算结果与现场物理流量计相比相对平均误差为3.33%，超过80%的数据点相对误差在±5%内，相对误差方差为0.050 8。综合分析表明：人工神经网络模型能够满足实际生产需要，且该模型结构简单，计算量小。人工神经网络模型的引用，为虚拟计量技术提供了一种新的工具和方法。

[1] NERBY G, SAETHER G, VELLA O J. A cost effective technique for production well testing[C]. Offshore Technology Conference,Houston, U.S.A, May1- 4, 1995, OTC-7 750.

[2] HALDIPUR P, METCALF G. Virtual metering technology fi eld experience examples[C]. Offshore Technology Conference, Houston,U.S.A, May5-8, 2008.

[3] 吴海浩, 王博, 王智, 等. 深水流动安全管理系统研究现状与应用[J]. 中国海洋平台, 2015, 30(2):4-9. [WU H H, WANG B, WANG Z, et al. The research situation and application of deepwater fl ow assurance and maragement system[J]. China Offshore Platform, 2015,30(2):4-9.]

[4] HAOUCHE M, TESSIER A, DEFFOUS Y, et al. Virtual fl ow meter pilot: Based on data validation and reconciliation approach[C]. SPE International Production and Operations Conference & Exhibition, Doha, Qatar, May 14-16, 2012, SPE-157 283.

[5] AJAYI A, FASASI T, OKUNS G. Real time fl ow estimation using virtual fl ow measurement techniques: A fi eld application in intelligent well completion[C]. Nigerian Annular International Conference and Exhibition, Lagos, Nigeria, August 6-8, 2012, SPE-162 948.

[6] WANG Z, GONG J, WU H H, et al. The development and application of virtual fl ow metering system in offshore gas fi eld[C]. International Pipeline Conference, 2014:V001T09A019.

[7] 吴永鹏. 基于虚拟计量技术的单井计量系统设计[J]. 船海工程, 2015, 44(5):56-58. [WU Y P. Design of single well measurement system based on the virtual measurement technology [J]. Ship & Ocean Engineering, 2015, 44(5):56-58.]

[8] 王珏, 李清平, 王凯, 等. 水下油气田虚拟计量技术应用[J]. 舰船科学技术, 2013, 35(9):118-122. [WANG J, LI Q P, WANG K, et al.Virtual metering technology for subsea fi elds [J]. Ship Science and Technology, 2013, 35(9):118-122.]

[9] 吴海浩, 王智, 宫敬, 等. 虚拟流量计系统的研制及应用[J]. 中国海上油气, 2015, 27(3):154-158. [WU H H, WANG Z, GONG J, et al. Development and application of a virtual fl ow meteing system [J]. China Offshore oil and Gas, 2015, 27(3):154-158.]

[10] 朱大奇, 史慧. 人工神经网络原理及应用[M]. 北京: 科学出版社, 2006. [ZHU D Q, SHI H. Principle and application of arti fi cial neural network [M]. Beijing: Science Press, 2006.]

[11] 蒋宗礼. 人工神经网络导论[M]. 北京: 高等教育出版社, 2006, 15-69. [JIANG Z L. Introduction to arti fi cial neural network [M].Beijing: Higher Education Press, 2006, 15-69.]

[12] 王智, 宫敬, 吴海浩, 等. 天然气井井口油嘴的两相流动特性及流量预测[J]. 油气田地面工程, 2013,(12):1-2,3. [WANG Z, GONG J, WU H H, et al. The fl ow characteristics of two-phase fl ow and prediction of natural gas wellhead choke [J]. Oil and Gas Field Surface Engineering, 2013,(12):1-2,3.]

[13] 王艳芝, 宫敬, 吴海浩. 水下油气田虚拟计量中的井筒传热计算[C]. 中国工程热物理学会论文, 2015.[WANG Y Z, GONG J, WU H H. Wellbore heat transfer calculation in virtual measurement of underwater oil and gas fi eld [C]. Proceedings of the Chinese Society of Engineering Thermophysics, 2015]

[14] 张立明. 人工神经网络的模型及应用[M]. 上海: 复旦大学出版社, 1993. [ZHANG L M. Model and application of arti fi cial neural network [M]. Shanghai: Fudan University Press, 1993. ]

[15] 蒲春, 孙政顺, 等. MATLAB 神经网络工具箱BP算法比较[J]. 计算机仿真, 2006, 23(5): 142-144. [PU C, SUN Z S, et al. Comparison of BP algorithms in Matlab NN toolbox [J]. Computer Simulation, 2006, 23(5): 142-144.]

[16] 陈龙, 张新政, 袁从. MATLAB 神经网络工具箱在河流水质预测中的应用[J]. 五邑大学学报, 2009, 23(1). [CHEN L, ZHANG X Z, YUAN C G, et al. Application of MATLAB neural network’ tool-box in river water quality prediction [J]. Journal of Wuyi University(Natural Science Edition), 2009, 23(1).]

AbstractWith the development of the oil industry to the deep water, underwater oil and gas production process have emerged and the traditional technology is facing many new problems. An alternative method for production estimation is represented by a Virtual Metering System (VMS) based on the analysis of the standard process parameters, available in almost all production system. The software is based on a methodology in which several models are included. This article mainly studies the application of an arti fi cial neural network in gas well measurement. Because the existing wellbore models cannot adjust to changes of production in a timely manner nor predict accurately, this article introduced an error back propagation arti fi cial neural network with highly nonlinear predictive ability. Arti fi cially debugged wellbore model results served as a data sample library to simulate the mapping relationship between all kinds of in fl uence factors and the gas well production. A gas well fl ow calculation model based on a back propagation neural network is set up by learning and training. Predicted results show that compared with a physical fl ow meter, the average relative error of the calculation results is 3.33%. More than 80% of the data points have a relative error within plus or minus 5%, which indicates a high prediction accuracy. Comprehensive analysis shows that the arti fi cial neural network model can meet the demands of practical production with the advantages of a simple model structure, fl exible form and less calculation. Application of the arti fi cial neural network model provides a new tool and method for virtual measurement technology.

Keywordssubsea production system; VMS; Arti fi cial Neural Network; gas-condensate pipeline; deepsea fl ow assurance

(编辑 马桂霞)

Research into calculation of natural gas well production based on an arti fi cial neural network

SONG Shangfei1, HONG Bingyuan1, SHI Bohui1, WU Haihao1, KANG Qi1, WANG Zhi2, GONG Jing1
1 National Engineering Laboratory for Pipeline Safety/ MOE Key Laboratory of Petroleum Engineering /Beijing Key Laboratory of Urban Oil and Gas Distribution Technology, China University of Petroleum-Beijing, Beijing 102249, China
2 Xi'an Changqing Science and Technology Engineering Co Ltd, Xi'an 710000, China

*通信作者，ydgj@cup.edu.cn; bh.shi@cup.edu.cn

2017-05-24

国家科技重大专项(2016ZX05028-004-001)、国家自然科学基金(51534007)、国家科技重大专项(2016ZX05066005-001)、国家重点研发计划(2016YFS0303704、2016YFS0303708)和中国石油大学( 北京) 科研基金(C201602) 联合资助

宋尚飞, 洪炳沅, 史博会, 吴海浩, 康琦, 王智, 宫敬. 基于人工神经网络的天然气井产量计算方法研究. 石油科学通报, 2017, 03:413-421

SONG Shangfei, HONG Bingyuan, SHI Bohui, WU Haihao, KANG Qi, WANG Zhi, GONG Jing. Research into calculation of natural gas well production based on an arti fi cial neural network. Petroleum Science Bulletin, 2017, 03: 413-421. doi: 10.3969/j.issn. 2096-1693.2017.03.038

10.3969/j.issn.2096-1693.2017.03.038