随机需求下基于M-CVaR的仓储服务定价决策研究

郭 泉

(苏州高博软件技术职业学院,江苏 苏州 215000)

随机需求下基于M-CVaR的仓储服务定价决策研究

郭 泉

(苏州高博软件技术职业学院,江苏 苏州 215000)

借鉴均值-条件风险价值，统一度量决策者的风险喜好、中性及厌恶水平，并据此研究考虑决策者风险偏好水平的仓储定价策略问题。建立了随机需求下基于仓储企业收益的均值-条件风险价值模型，经过对M-CVaR模型的分析计算，得出仓储企业的最优定价，并通过数值算例，与以收益最大化为目标所得出的最优值进行比较分析。随机需求下考虑决策者风险偏好水平的仓储企业定价策略更加科学合理，对仓储企业具有现实的指导意义。

均值-条件风险价值；随机需求；仓储企业；定价策略

仓储总是出现在物流各环节的接合部[1]，在现代物流中占有核心地位，是物流管理的关键环节之一[2]。近年来，我国物流业虽迅速发展，但也存在一些问题，就仓储企业而言，储存、保管等基础仓储服务项目盈利空间正逐渐缩小，传统仓储业已处于完全竞争状态[3]。此状态下，仓储企业合理制定价格变得更为重要，因为合理的定价策略及价格水平可以收回成本、获得收益并取得仓储服务需求商的信任，有利于巩固和扩大市场份额。同时对于仓储服务需求商而言，仓储企业服务价格及收费标准的合理、公开，可大大降低由于信息不对称所引起的交易成本及其他成本，使仓储服务需求商可以专注于其核心业务[4]。

部分学者对第三方物流服务企业的定价问题进行了研究：余木红[5]等研究了以利润最大化为目标的第三方物流企业运输定价问题；谢天帅[6]等提出了第三方物流服务定价的分析框架；白燕华[7]等运用博弈原理改进传统的第三方物流企业的定价机制；桂思思[8]从信息商品的视角研究了第三方物流服务定价策略。这类文献多侧重定性研究，即便涉及某些定量方法，也是假设市场需求相对确定，这与现实情况不符，假设市场需求为随机需求更符合实际；此外，这些文献将第三方物流服务企业整体作为研究对象，肯定了第三方物流在供应链整体控制方面的重要作用，但在现代物流系统中占有重要位置的仓储企业却没有受到学术界足够的重视，因此有必要对随机需求下仓储企业定价策略进行研究。

由于实践中供应链成员企业的风险态度已成为影响定价、订购量等决策的重要因素[9]，目前部分学者对考虑风险偏好的制造商及零售商定价策略进行了研究：李贺[10]等研究包括顾客行为和风险因素的风险规避厂商定价及配给问题；蒋敏[11]基于VaR和CVaR通过建立多损失条件风险值模型求得风险厌恶面包制造商的最优批发价格；王虹[12]等研究由风险规避的制造商和零售商在信息对称与非对称条件下各自的定价策略。上述文献均基于供应链成员企业为风险中性或厌恶研究了其定价策略，成果有一定的应用价值，但忽略了现实中存在风险喜好型的决策者。Jammernegg等[13]经过实证调查认为决策者的风险偏好分为风险中性、喜好、厌恶三种类型，所以需要运用能够统一度量三种风险偏好的模型研究定价问题。均值-条件风险价值模型（M-CVaR）能够统一度量三种风险偏好水平，借鉴该模型，研究随机需求下仓储企业的定价策略更能满足现实需求，对现实中仓储企业实现科学合理的定价有重要的指导意义。

1 随机需求下基于M-CVaR的仓储企业定价策略研究

本模型假设仓储企业提供同等级服务，其仓储能力为一个定值L；仓储服务需求商需求的仓储能力为N，且仓储能力能够满足需求；仓储能力的残值为O；由于模型中决策者具有风险偏好，在决策过程中已经将机会成本考虑在内，所以模型不再特别列出机会成本；p为仓储企业为仓储服务需求商提供服务所收取的单位价格，c为单位成本；由于仓储服务需求的商需求与仓储企业定价有关，且随机，本文借鉴Petruzzi和Dada[15]提出的需求加法模型：其中，是随机变量，的密度函数和分布函数，和分别为其均值和标准差，并给出

基于以上假设，仓储企业的收益函数表示如下：

根据Ernst(1970)和Thowsen(1975)，定义代入（1）式可得：

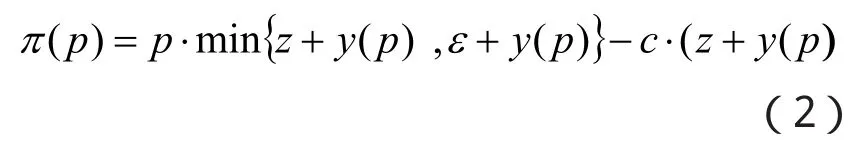
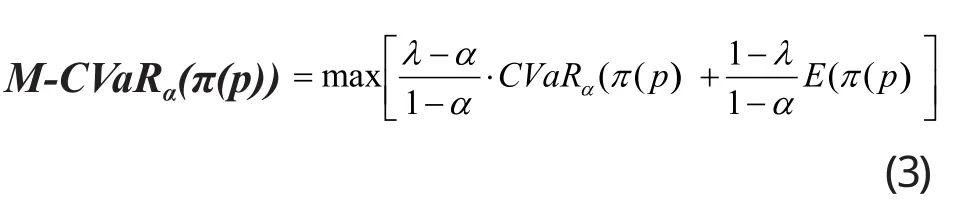
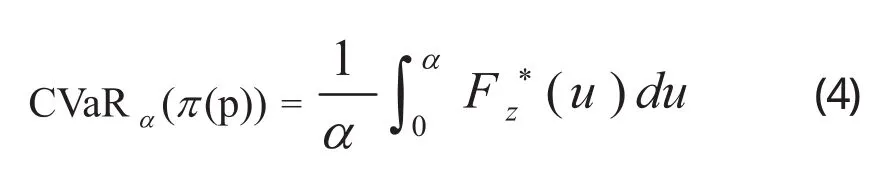
下面研究仓储企业的M-CVaR模型:

可得仓储企业基于收益的M-CVaR模型：

根据函数极值在实际问题中的应用，令(11)式=0可得z的最优值

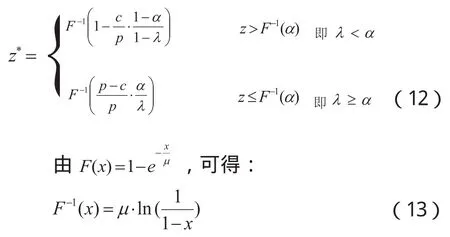
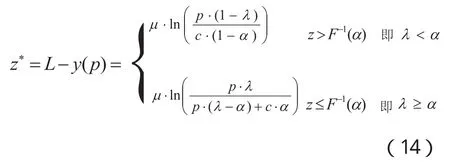
由于当z取其最优值时，满足式（14）的p也同时取其最优值，最终可得：

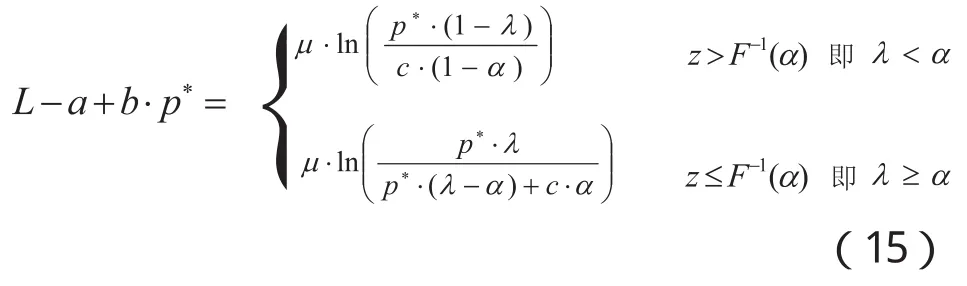
其中,Jammernegg等[14]证明了等价于，反之亦然。当仓储企业的定价满足(15)式时，实现最优定价。

2 数值算例

为了便于计算，算例中的数据部分是假定的，在实际应用过程中，可根据实际数据进行矫正。假设仓储企业的仓储能力L=500个单位；仓储企业的单位成本ε的分布函数水平和决策者悲观系数λ见下表，根据以上数据可得基于M-CVaR的随机需求下仓储企业最优定价，具体结果见表一。

为进行对比，同时计算以收益最大化为目标所得的最优定价p'：

根据式（6），对z求导数可得：其均值，置信

表1 随机需求下基于M-CVaR的仓储企业最优定价

令式（16）为0，可得使收益取最大的z'

由于当z取最优值z'时，满足式（17）的p也同时取其最优值p'，又最终可得：

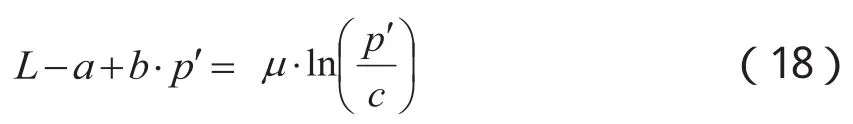
根据式（18），代入数据，可得以收益最大化为目标的最优定价

从表1可以看出，在给定的置信水平下，随着决策者的悲观系数从小于增加到大于，仓储企业的最优定价逐渐增大，并且发现，当等于时，不同的对应的最优定价是相等的，也就是说只要决策者为风险中性，决策者做出的定价无差别，且等于传统上以收益最大化为目标所得出的最优定价，可见决策者为风险中性可以等价于传统模型的不考虑决策者风险偏好，这进一步验证了随机需求下基于M-CVaR的仓储企业定价模型的适用性。

3 结论

本文突破假设供应链成员风险偏好为风险厌恶和中性的限制，运用均值-条件风险价值模型研究了随机需求下考虑决策者风险偏好水平的仓储企业定价策略。假设仓储服务需求商的需求为随机需求，借鉴报童模型中经典的加法模型；建立了仓储企业基于收益的M-CVaR模型；理论推导及数值算例，均证明决策者风险偏好会影响仓储企业的最优定价，且一定置信水平下的趋势为：最优定价随着决策者悲观系数的增大而增大；并给出决策者为风险喜好（）、中性（）及厌恶（）情况下最优定价满足的等式。因此实际应用中，仓储企业应结合自身风险态度，根据相关数据计算企业最优定价。

虽然本文基于M-CVaR研究了随机需求下仓储企业定价策略，对仓储企业既考虑风险又最大化收益具有一定的现实指导意义。但也存在继续研究的问题，比如对提供不同级别仓储服务的仓储企业进行研究。

[1]王洋，邵彦慧，王永涛. 我国仓储业的走向—第三方仓储管理[J].物流工程与管理,2010,(4):19-20.

[2]李超锋.我国仓储企业的盈利模式和发展方向探讨[J].物流工程与管理，2010，32(8):112-113.

[3]许茂增，贾禹，谢静.我国仓储企业盈利模式及发展方向[J].重庆交通大学学报( 社科版)，2013，13(3):43-46.

[4]田成. 第三方物流企业仓储服务价格制定研究与实践[D].大连海事大学,2004:23.

[5]余木红，周凌.第三方物流运输服务定价模型与研究[J].物流工程与管理，2010，32(10):4-6.

[6]谢天帅,李军.第三方物流服务的定价分析框架[J].商业研究，2009，(11):23-26.

[7]白燕华，张迎.第三方物流企业传统定价机制综述［J］.中国证券期货，2011，（4）：66-67.

[8]桂思思.第三方物流核心服务定价方式新探[J].科技创业，2012，(7)：80-81.

[9]Andy A T. Risk sensitivity in distribution channel partnerships:Implications for manufacturer return policies[J].Journal of Retailing，2002，78(2):147-60.

[10]李贺，张玉林.考虑顾客行为和风险因素的定价及配给研究[J].管理工程学报，2014,28(2):151-159.

[11]蒋敏.一种多损失条件风险值的双层规划模型及应用[J].系统工程理论与实践，2013，33(4):926-933.

[12]王虹，孙玉玲，周晶.制造商信息私有条件下的双渠道供应链定价决策[J].运筹与管理，2013，22(6)：117-122.

[13]Werner Jammernegg,Peter Kischka.Risk preferences and robust inventory decisions[J].Int.J.Production Economics，2009:269-274.

[14]Werner Jammernegg,Peter Kischka. Risk-averse and risktaking newsvendors: a conditional expected value approach[J].Review of Managerial Science，2007,1(1): 93-110.

[15]Nicholas C.Petruzzi，Maqbool Dada.Pricing And The Newsvendor Problem—A Review[J].Operations Research，1999，47(2)：183-194.

［编校：杨 琴］

The Decision Making Research on Storage Service Pricing on the Basis of M-CVaR under Random Demand

GUO Quan
(Global Institute of Software Technology, Suzhou Jiangsu215000)

M-CVaR is used for reference, and the decision makers’ risk preference, neutrality, and aversion are taken into consideration. And accordingly, the warehousing pricing strategy is studied. The M-CVaR model is built according to warehousing enterprises’ benefits under random demand. The best price is offered according to the analysis and calculation of the M-CVaR model. And through numerical examples, the given optimal price is comparatively analyzed with the optimum value obtained with profit maximization as its goal. According to the analysis, the warehousing pricing strategy on the basis of the decision makers’ risk preference under random demand is more reasonable and has practical guiding significance for warehousing enterprises.

M-CVaR; random demand; warehousing enterprises; pricing strategy

F253

A

1671-9654(2017)03-0089-04

10.13829/j.cnki.issn.1671-9654.2017.03.027

2017-04-10

郭泉（1985- ），女，山东沂南人，讲师，在读博士研究生，研究方向为工商管理。

本文为苏州高博软件技术职业学院重点课题“苏州炎鑫炎机械科技有限公司低碳库存管理优化”（编号：GIST2017-H001）阶段性研究成果。