楔顶双孔受感器试验数据处理方法研究
黎 琨
(中国航发湖南动力机械研究所,湖南株洲,412002)
楔顶双孔受感器试验数据处理方法研究
黎 琨
(中国航发湖南动力机械研究所,湖南株洲,412002)
楔顶双孔压力受感器可以用来获取三维动态流场数据。本文分别采用三次样条插值、最小二乘法拟合和线性插值等三种方法,对基于楔顶双孔高频压力受感器试验数据进行了分析研究,结果表明线性插值法较样条插值、最小二乘法具有更高的精度。
楔顶双孔受感器;样条插值;最小二乘法;线性插值
0 引言
未来航空发动机的需求,使得压气机部件必须具有高负荷、高效率以及宽广的工作范围,而压气机是否能满足总体要求,仅仅通过数值仿真计算不能反应实际情况。一般情况下,部件性能试验件是比较好的选择,基本能验证设计质量,但试验数据获得及分析,则显得尤为重要和关键。目前,由于航空发动机高功重比、小迎风面积的限制,压气机转子流道内部空间十分有限,内部流动呈现出复杂的强三维性和强非定常性,测试现场环境恶劣,因而很难采用激光多普勒测速仪、粒子图像速度仪等先进的光学测试技术或热线技术测量压气机内部流场[1-3]。先进的高频压力受感器技术具有比热线更坚固,比光学测量更简单,内置高频动态压力传感器后能测出压气机内部流场动态参数等优点,受到国内外研究人员的青睐。
测量三维动态流场,应用较多的是五孔压力受感器,也有应用七孔、四孔压力受感器的,多孔压力受感器需要内置多个微型动态压力传感器,因而造成受感器头部尺寸较大,对被测流场产生较大的影响,导致试验结果不能真实反应被测流场。而本文使用的楔顶双孔压力受感器其本质是对四孔压力受感器的分解使用,通过绕自身轴线正反向旋转一定的角度以获取不同的压力值解决了上述难题。由四孔压力受感器测量原理,根据四个压力值可以计算出两个方向校准系数,然后将两个方向校准系数代入到校准曲线,插值得出两个方向角、总压校准系数和静压校准系数。插值方法是否合适直接影响着试验结果的准确性。本文对三次样条插值、最小二乘法拟合和线性插值三种方法进行了研究,分析得出了适合楔顶双孔受感器数据处理的方法。
1 楔顶双孔受感器
1.1 受感器结构
本文研究的楔顶双孔受感器由支杆和头部组成,直径分别为8mm和4mm,头部呈楔形,外形如图1所示,在头部的圆柱面和斜面各开有一个测压孔,直径分别0.5mm和1mm。2个Kulite公司的XCQ-062微型高频动态压力传感器封装在受感器头部,通过内部管路与测压孔相通。将封装好的受感器置于激波管内校准,校准结果表明受感器的两个孔谐振频率相近,且频响均超过了20000kHz,频响较高。

图1 楔顶双孔受感器外形图
1.2 测量原理
楔顶双孔压力受感器通过绕自身轴线正反向旋转一定的角度 获取四个不同的压力值,如图2所示,其本质是对四孔压力受感器的分解使用。由图可知正孔压力为1P、斜孔压力为4P、受感器逆时针和顺时针方向旋转α角获得的压力分别为2P和3P。
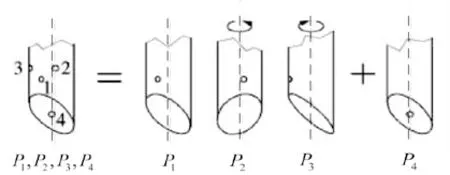
图2 楔顶双孔高频压力受感器测量原理图[4]
根据四孔压力受感器测量原理,定义偏转角系数Kα、俯仰角系数Kβ、总压系数tK、马赫数系数MK 和静压系数sK,分别如公式(1)~(5)所示 :
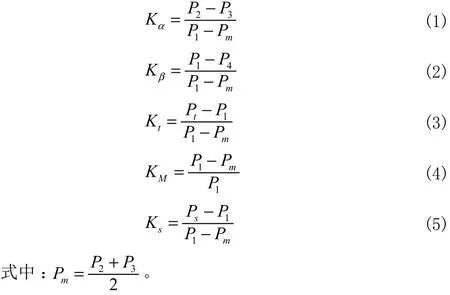
1.3 受感器气动校准
本文在某校准风洞对受感器进行了校准,校准范围为:偏转角 -30º~+30º(间隔 5º)、俯仰角 -30º~+30º(间隔 5º)、马赫数0.4~0.7(间隔0.1)。图3为受感器在校准马赫数0.5时,受感器的气动性能图,结果表明受感器在校准范围的边界处梯度略大,其他范围的气动特性良好。其他校准马赫数下系数分布与图3相似。

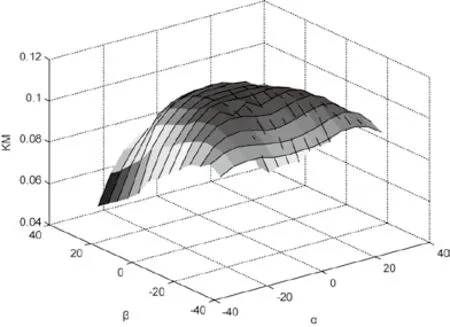
图3 受感器气动性能(Ma=0.5)
2 数据处理方法
应用楔顶双孔高频压力受感器测量三维流场时,可以测得虚拟四孔受感器1~4孔所对应的压力 P1、P2、P3和 P4,按下述步骤进行数据处理。
(1)将压力测量值 P1、P2、P3和 P4代入到公式(1)和(2)可求出α方向校准系数Kα和β方向校准系数Kβ。
(2)任取 (M a )0为某一状态,由Kα和Kβ通过在角度校准特性曲线、总 压 校 准特性曲线f3(M a,α β)和静压校准特性曲线f4(Ma,α β)中插值可以得出气流偏转角α、俯仰角β、总压系数(Kt)1和静压系数(Ks)1。
(3)将 P1、P2、P3、 和(Kt)1、(Ks)1代入式(3)、(5)计算可得(Pt)1、(Ps)1。
(4)由(Pt)1、(Ps)1计算可得(M a)1。
(5)重复上述步骤,每次计算都用当前计算结果(M a )n代替前一次的计算结果(M a )n−1进行计算,直到前后两次计算结果之差小于所要求的精度,这时的结果即为被测流场的测量结果。
在插值过程中,国内外学者使用了不同的方法,本文基于楔顶双孔高频压力受感器试验数据对三种不同的插值方法进行了研究。
2.1 三次样条插值法
三次样条具有连续二阶导数,其曲线的光滑性好,本质上是一段一段的三次多项式拼合而成的曲线。在拼接处,不仅函数是连续的,一阶和二阶导数也是连续的。
假设给定 n + 1 个点 x0<x1<x2<…<xn,下面利用S( x)的二阶导数值 S ′(xj) = Mj(j=0,1,2,…,n)表达 S ( x),由于三次样条插值函数 y = S ( x)在每个子区间 [ xj, xj+1]上为三次多项式,故 S ′(x)在[xj, xj+1]上是线性函数,可表示为 :

其中,hj= xj+1−xj。
对上式两端在区间 [ xj, xj+1]上连续两次求积分,得三次样条表达式:

使用三次样条插值法进行数据处理,这种方法具有良好的收敛性和稳定性,又有二阶光滑度,在原理上具有较高的精度,因此在理论上和应用上都具有重要的意义。
2.2 最小二乘法
最小二乘法的基本思想是根据经验或定性分析构造含有待定系数(或称参数)的拟合函数 ()g x,然后根据最小二乘原则,即要求 ()g x在节点处与给定数据的误差的平方和达到最小的原则确定系数,从而得到所需要的近似函数 ()g x。利用公式可以表述如下:
给定n组数据(xi, yi)(i=1,2,…,n),求m次多项式:

使 F ( a*, a*, …,a*) = min F ( a, a ,… ,a )
这里 称为方差。
2.3 线性插值法
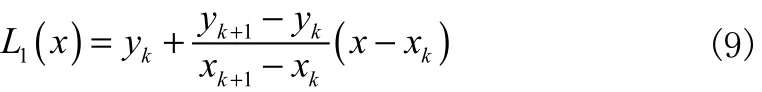
根据公式(9),只要知道区间 [ xk, yk+1]范围内任意x值就可以直接计算出y值了。
本文使用的线性插值方法如下。图4为插值方法图,其中横轴为俯仰角系数Kβ,纵轴为偏转角系数Kα,直线AB对应的偏转角为αAB,直线CD对应的偏转角为αCD,A、B、C、D四点对应的坐标分别为(xA, yA)、(xB, yB)、(xC, yC)、(xD, yD),为了插值出待测点S(xS, yS)所对应的偏转角αS,本文首先过点S做一条平行于纵轴的直线,该直线与AB的延长线相交于点E(xE, yE),与直线CD相交于点F(xF, yF),根据公式(13)得点E及点F的纵坐标,再由点E及点F的纵坐标插值出待测点S所对应的偏转角αS,如式(10)~(12)所示。

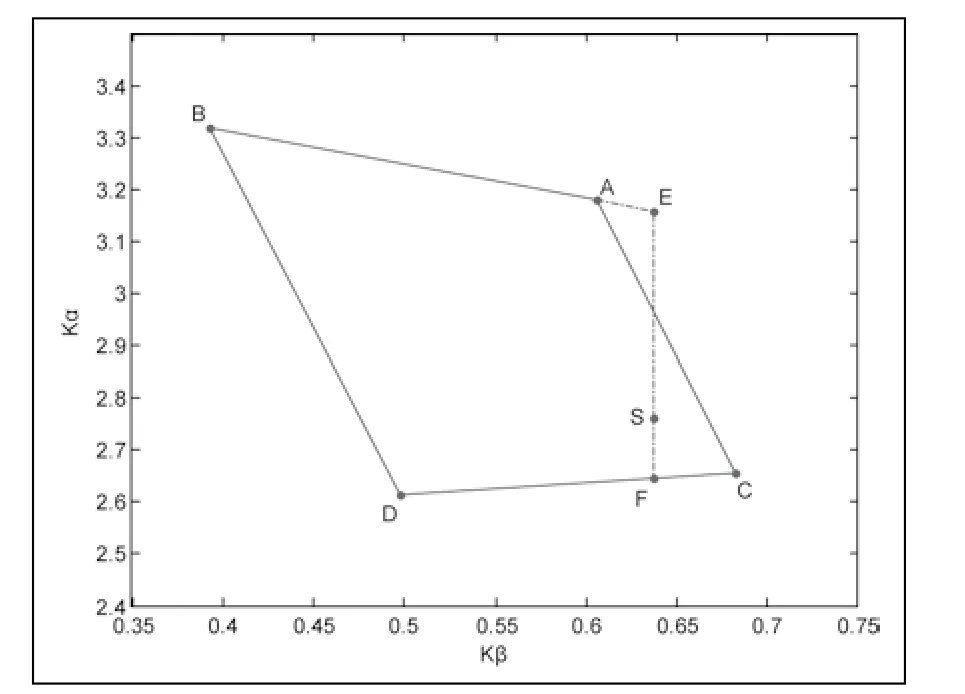
图4 插值方法图
3 试验结果比较
为研究上文所述三种数据处理方法对试验结果的影响,本文对楔顶双孔高频压力受感器在马赫数0.5下进行校准试验,获取了俯仰角范围为±30º(间隔5º),6个不同偏转角的试验数据。将实际测量值与插值结果进行比较,可得样条插值、最小二乘法拟合和线性插值3种方法的最大误差,如表1所示。从表1中可以看出,使用不同的插值方法得到的结果有着较大的差异。其中样条插值最大误差为0.5º,最小二乘法的最大误差为0.38º,线性插值的最大误差为0.24º。

表1 三种插值法最大误差对比表
应用同样的方法对受感器在马赫数0.4、0.6、0.7下的校准数据进行分析,同样可以得出线性插值法的误差最小。
4 结论
本文研究的楔顶双孔高频压力受感器可以真实有效的获得三维动态流场数据,同时通过对比发现,线性插值法较样条插值、最小二乘法具有更高的数据处理精度。
[1]马宏伟,贺象,单晓明等.一种测量跨声速多级压气机转子出口二维流场的方法[J].推进技术,2013,6.
[2]李井洋,马宏伟,贺象.楔顶双孔探针测量跨声多级压气机转子出口三维动态流场的方法[J].航空动力学报,2012,10.
[3]岳国强,韩万金,芦文才等.五孔探针实验数据处理的线性插值法[J].热能动力工程,2004,9.
[4]Persico G, Gaetani P, Guardone A. Design and analysis of new concept fast-response pressure probes[J]. Measurement Science and Technology, 2005, 16(9): 1741-1750.
Research on Date Processing Method of Testing for Two-hole Tipwedge Pressure Probe
Li Kun
(AECC HuNan Avation Powerplant Research Institute,Zhuzhou Hunan,412002)
The 3D dynamic field data can be got by the two-hole tip-wedge high frequency pressure probe. The test data is analyzed by cubic spline interpolation, least squares method and linear interpolation three methods in this paper. The results show that the linear interpolation was the same precision with spline interpolation for the characteristics of a good probe and the linear interpolation could guarantee the accuracy of interpolation based on the characteristic curve of the probe does not change for the characteristics of a poor probe. Compared with spline interpolation and least squares method, the linear interpolation method has more extensive adaptability.
two-hole tip-wedge probe;spline interpolation;least squares method;linear interpolation

