大型排土机平衡性和稳定性的优化计算
孙 刚
(1.太原重工股份有限公司技术中心, 2.矿山采掘装备及智能制造国家重点实验室,山西 太原 030024)
大型排土机平衡性和稳定性的优化计算
孙 刚1,2
(1.太原重工股份有限公司技术中心, 2.矿山采掘装备及智能制造国家重点实验室,山西 太原 030024)
介绍了大型排土机平衡性及稳定性的设计规则,结合现代设计方法,采用三维建模,简化传统的排土机平衡性和稳定性计算公式,对大型排土机平衡及稳定性方面进行了优化计算,提高了计算速度和准确度,确保排土机工作时的平衡性和稳定性。
大型排土机 平衡性 稳定性 现代设计理论与方法 优化计算
针对岩石硬度的不同,通过增加轮斗系统或破碎环节而取消大汽车运输的连续或半连续开采工艺,因具有高效、节能、环保等特点,是大型露天矿山开采工艺的发展趋势。排土机作为连续或半连续开采工艺系统中的关键设备之一,其主要在排土场完成由带式输送机从采场运送来的物料并有序排弃。太原重工股份有限公司(以下简称太重)2015年与太钢袁家村铁矿签订了1台9 000 t/h排土机的供货合同,该套设备为国内规格最大、结构最先进、智能化水平最高的排土机,现已运行半年,各项指标达标,运行状况良好。
排土机整机的平衡和稳定性直接影响其安全使用,因此在设计过程中必须对排土机整机的平衡和稳定性进行验算。传统的验算方法步骤复杂,计算精度欠佳,往往通过放大安全系数的方法来抵消计算精度上造成的误差。随着三维软件的普及,在三维环境中很方便对排土机精确建模,并确定各部件重心位置,可以简化传统计算方法,优化计算排土机的平衡和稳定性,并指导排土机实际设计。
大型排土机整机由上部部件、下部部件、液压系统、电控系统等组成。上部部件主要由平台、塔架、配重臂、排料臂、受料臂、三脚架、司机室、工作间、电气室、配重等组成。下部部件主要由履带、底架梁等装置组成(见图1)。
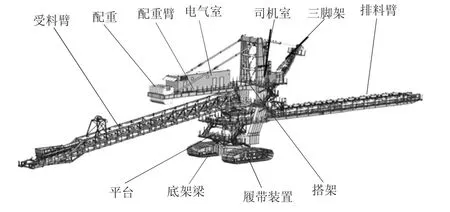
图1 排土机三维模型
1 排土机平衡性的优化计算
1.1 排土机平衡性的设计规则
排土机的下部结构和上部结构之间通过一个球柱联合式回转支撑连接,该回转支撑同时承受轴向载荷、径向载荷和倾覆力矩等联合载荷。排土机的平衡是指通过在配重臂上添加合理配重,使上部部件在各工作状态下,其作用力的合力和合力矩不得超出回转支承的承载能力,并尽量使回转支撑各辊子受力大小和受力周期均匀。
根据图1排土机的结构组成结合其工作特点分析,排土机上部部件产生的轴向载荷主要由受料臂、配重、配重臂、电气室、司机室、三脚架、排料臂、平台、塔架产生。排土机上部部件产生的倾覆力矩由于受料臂的吊点通过其回转中心不产生倾覆力矩,故其主要由配重、配重臂、电气室、司机室、三脚架、排料臂、平台、塔架产生。其中轴向载荷分为两种极限工况:排料臂满载和排料臂空载。倾覆力矩的大小与排料臂的位置和排料臂上物料的多少有关系,排料臂的位置根据工艺要求分为上排、平排和下排,每种排弃工艺又分为两种极限工况:排料臂空载和排料臂满载。
根据大型露天矿的实际工作制度,排土机正常运行以后,一般每天工作时间为16~18 h,休息时间为6~8 h,再考虑的到设备的维护、节假日等因素,一年下来工作时间和停机时间各占一半。同时,参照国外相关资料并结合选型的合理性和经济性,我们把排土机上部部件产生的倾覆力矩的力臂限定在以回转支撑中心为原点,1 m为半径的圆内,在排土机非工作状态时,上部部件的力矩限定在距回转支撑中心-1 m~0之间,在排土机工作状态时,上部部件的力矩限定在距回转支撑中心0~1 m之间。
1.2 方法优化后的配重计算
通过对排土机三维建模求得回转支撑以上各个部件的自身质量和重心位置后,可通过静力学基本原理来确定各种极限工况下的极限配重。
1.2.1 确定满载工况最大配重G1
排料臂水平满载,整机(含配重)重心位于-1m处。
1.2.2 确定满载工况最小配重G2
排料臂水平满载,整机(含配重)重心位于1m处。
1.2.3 确定空载工况最大配重G3
排料臂水平空载,整机(含配重)重心位于-1m处。
1.2.4 确定空载工况最小配重G4
排料臂水平空载,整机(含配重)重心位于1m处。
1.2.5 取实际配重G

1.2.6 验算
确定完实际配重后,在三维模型中求各种工况下的实际轴向载荷Fi和倾覆力矩Mi,并确定极限工况下的最大轴向载荷F和倾覆力矩M,进一步进行回转支撑的选型。
1.3 回转支撑的选型
确定完排土机的配重后,验算所选用的回转支撑,根据排土机的工作特点,其回转支撑的转速很低并且是间歇性工作,因此,其计算按静载荷计算。目前,对于回转支撑的选型,采用承载曲线图(载荷—力矩图)方法,如图2所示。倾覆力矩M用垂直轴表示,轴向载荷F用水平轴表示,线1表示回转支撑的许用静载荷承载能力极限曲线;线2表示回转支撑额定使用寿命为3×104r时的动载荷承载能力极限曲线;一组平行线表示螺纹强度等级为8.8级,10.9级,12.9级极限载荷能力曲线。每种回转支撑对应一种承载曲线图。

图2 回转支撑承载曲线图
将回转支撑实际承受的轴向载荷F和倾覆力矩M在承载曲线图的水平轴和垂直轴上找到相应点,分别作该点水平线和垂直线相交于A点。然后根据A点所处的位置,就可以判断所设计的回转支撑静承载能力是否满足使用要求。
当A点处于曲线1和选用的某等级螺栓极限载荷曲线下时,满足静载荷使用要求。
从承载曲线坐标原点经A点联线与静载荷承载曲线1交点于D,D点对应的轴向载荷或倾覆力矩值,可得到该规格回转支撑的静载荷安全系数 fs。

同理,联线与动载荷承载曲线2交点于G点,可得到该规格回转支撑的寿命载荷系数fe,进一步可以对恒定载荷下的寿命预测。

恒定载荷使用寿命预测:

式中:Lf为轴承使用寿命,r;fe为轴承寿命载荷系数;ε为寿命系数,球轴承ε为3,辊子轴承ε为10/3。
2 方法优化后的排土机稳定性计算
2.1 计算规则(见下页图3)
通过引进稳定性系数K来反映排土机的稳定性,其值为对于排土机倾覆轴线的复原力矩Mf与倾覆力矩Mq之比,其值大于1,表示设备不会发生倾翻,即:


图3 排土机稳定性计算图
在计算稳定性时,排料臂可能处于以下三种位置:
1)排料臂平行于排土机履带前进方向,这时排土机两条履带的最前滚轮与土壤的接触点连线O1—O1是它的倾覆轴线。
2)排料臂垂直于排土机履带前进方向,这时排土机一侧履带连接支承滚轮外缘的直线O2—O2是它的倾覆轴线。
3)排料臂处于排土机履带的对角线方向,这时排土机的倾覆轴线O3—O3通过前滚轮与履带环之最外接触点,且垂直于排料臂在水平面上的投影。
以上三种工况,因a2最小,因此第二种工况被确定为最危险工况。
2.2 排土机的稳定性优化计算
排土的稳定性,要按以下两种情况进行计算。
2.2.1 正常工作时最不利的情况
排土机处于水平地面上,排料臂与履带前进方向成90°,排料臂水平位置排土,物料满负荷运行,轴线O2—O2为倾覆轴线。通过在UG三维模型中求各部件重心位置和质量后,求倾覆力矩:

式中:Gq为满负荷运行时排料臂和三脚架自身质量及其上物料的合重力;Lq为在此工况条件下,排料臂和三脚架自重及其上物料重心到倾覆轴线的水平距离;Fs为风压力;h为风压力臂。
求复原力矩:

式中:Gf为上部部件(包括配重)和下部部件的重力;Lf为上部部件和下部部件的重心到倾覆轴线的水平距离。
分别计算得到倾覆力矩Mq和复原力矩Mf后求得稳定性系数:
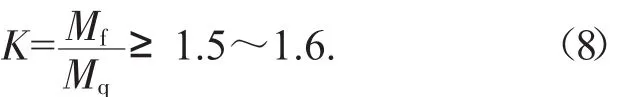
2.2.2 排土机在上坡和下坡运行时的情况
1)上坡时,排土机一般可爬连续坡度为5°,排料臂在运行前方,迎风前进,以O4—O4为倾覆轴线计算倾覆力矩和复原力矩,如图2所示。
在UG三维模型下,可以将倾覆力矩、复原力矩公式简化为:

式中:Gq3为排土机上部部件的整个自身质量,Lq3为上部部件的重心到倾覆力矩的水平距离,hq3为上部部件的重心距地面垂直高度,Gf3为下部部件和排料臂和三脚架自重及其上物料的合重力,Lf3下部部件和排料臂和三脚架自重及其上物料的重心到倾覆力矩的水平距离,hf3为下部部件和排料臂和三脚架自身质量及其上物料的重心距地面垂直高度。
2)下坡时,排土机一般可下连续坡度为5°,起重臂在运行前方,顺风前进,以O1—O1为倾覆轴线计算倾覆力矩和复原力矩。
在UG三维模型下,可以把倾覆力矩、复原力矩公式简化为:

式中:Gq4排料臂和三脚架自身质量及其上物料的合重力;Lq4为在此工况条件下,料臂和三脚架自身质量及其上物料的合自身质量的重心到覆力矩的水平距离;hq4为料臂和三脚架自身质量及其上物料的合自身质量的重心到地面的垂直高度;Gf4为上部部件和下部部件的重力;Lf4为在此工况条件下,上部部件和下部部件重心到覆力矩的水平距离;hq4为上部部件和下部部件的重心到地面的垂直高度。
一般,排土机在上坡和下坡时取K≥1.5。
针对上述两种极限工况对排土机的稳定性进行验算通过后,说明排土机结构设计合理,若验算通不过,需重新设计结构,直到验算通过为止。
3 结语
通过对大型排土机在虚拟环境中的精准三维建模,得到各部件的重量和重心坐标后,并通过上述方法计算排土机的平衡性和稳定性,具有计算简单,结果准确的特点。同时,该套设备在现场使用情况良好,进一步佐证了该算法的正确性。
[1] 潘兆庆,周济.现代设计方法概论[M].北京:机械工业出版社,1991.
[2] 关振宇.NX6机械设计基础教程[M].北京:人民邮电出版社,2009.
(编辑:苗运平)
The Optimal Calculation for the Balance and Stability of Large Spreader
Sun Gang1,2
(1.Technology Center of Taiyuan Heavy Industry Co.,Ltd.,2.State Key Laboratory of Mining Equipment and Intelligent Manufacturing,Taiyuan Shanxi 030024)
The design rules of balance and stability of the spreader are introduced.Combined with modern design method,using three-dimensional modeling,traditional calculation for the balance and stability of spreader is simplified,and optimize calculation for the balance and stability of spreader is conducted so as to improve the calculation speed and accuracy,and ensure balance and stability when the spreader is working.
large spreader,balance,stability,modern design theory and method,optimization calculation
TD422.4
A
1672-1152(2017)04-0033-03
10.16525/j.cnki.cn14-1167/tf.2017.04.13
2017-04-25
矿山采掘装备及智能制造国家重点实验室配套经费(201605D111008-02)
孙刚(1982—),男,毕业于哈尔滨工业大学,硕士,工程师,现就职于太原重工股份有限公司技术中心,从事矿山设备的研究与设计工作。

