救护车辆配置优化设计

伏紫妍，张 勇

(苏州大学城市轨道交通学院，江苏苏州 215006)

救护车辆配置优化设计

伏紫妍，张 勇

(苏州大学城市轨道交通学院，江苏苏州 215006)

针对当前医疗急救资源难以满足实际需求的情况，为了提高救护效率，缩短急救服务的响应时间，对救护车辆的配置调度进行了研究。在提出联合排队模型的基础上，给出了一系列评价急救系统性能的指标，并用C++语言实现了该算法。最后以苏州市内环线急救系统为例，验证了模型的有效性。结果表明，联合排队模型可以对急救系统的救护车辆配置进行有效评价，据此可以提出合理的调整意见。研究结果可为城市急救系统的救护车配置、调度等问题提供决策依据。

排队论；医疗急救资源；救护车配置；联合排队模型；C++语言

近些年来，医疗急救与社会需求间的矛盾不断突出。图1是苏州市急救中心公布的2013年1-9月份急救电话呼叫量、救护车出车数及危重病人抢救数的统计图，显然急救资源无法满足现有需求。造成该问题的原因表面上看是救护车数辆严重不足，实际上还包括以下2个原因：1)道路拥堵，救护车通行优先权得不到保证；2)急救资源(如救护车、全科医生等)匮乏，调度缺乏合理性。因此，在供给不足的情况下，合理配置、调度现有的救护资源已成为关键。

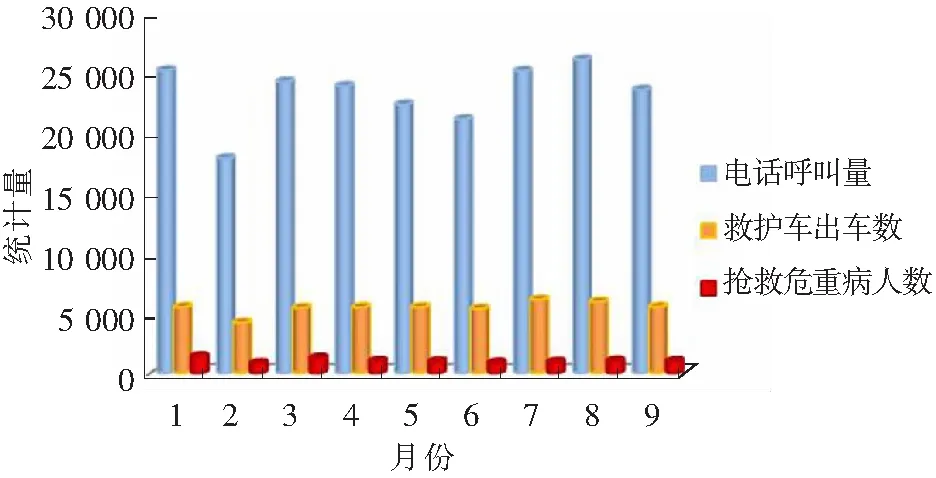
图1 苏州市急救中心2013年1月到9月呼叫统计Fig.1 Call statistics in Suzhou Emergency Center from January to September in 2013

系统中救护车辆的分布应该确保足够的覆盖面和尽量短的响应时间。国内外关于救护车的选址和配置问题的研究很多。BROTCORNE等[1]概述了救护车辆选址的相关模型，主要分为确定性模型和随机性模型。确定性模型忽略了救护车辆的随机性，而随机性模型揭示了救护车运作过程是一个排队系统的事实，并且时常伴随呼叫的丢失。随后，ANDERSSON等[2-3]对救护车调度问题提出了动态调整模型，以求减少伤病员的等待时间。在车辆的选址定位问题方面，HAKIMI[4]最早提出了网络上的P-中值问题与P-中心问题，即在一个网络中选定一个或者多个设施的位置使得设施点与需求点之间的最大距离最小。DASKIN等[5]解决了上述模型的启发式算法难以求得最优解的问题。而TOREGAS等[6]研究选址研究集合覆盖模型，运用线性规划求解在预定的时间限制内的覆盖问题。该模型旨在解决设施点位置数目已知、要求选取最少位置的问题，且能在规定时间内给所有需求地区提供紧急服务。然而，随着事故发生需求的空间分布以及设施选址投入成本等输入量变得更为复杂和不确定，以往的静态选址模型已不能满足发展需要。

对于救护车辆的配置调度而言，除了需要确定车辆的位置，更重要的是每处设施需要配置多少辆救护车，各设施间的车辆如何调度，才能更好地满足系统的急救需求。因此，本文紧接着对救护车的调度指派问题进行了研究。LARSON[7-8]提出了超立方排队模型，首次将排队论嵌入到车辆的定位分配中。该模型提供了给定服务点的状态概率及相关的性能指标。JARVIS[9]提出了一个服务器和客户都依赖于服务时间的观点，对上述方法进行了优化。随后LARSON等[10]对巡逻车的3种状态提出了3n模型： 1)忙于服务呼叫， 2)忙于巡逻活动中， 3)空闲。他们通过不超过5台的服务器验证了该方法。IANNONI等[11]将超立方体嵌入到遗传算法的框架，沿着公路定位多辆应急车辆，保证多个派遣。然而，这些研究基本集中在高速公路等线状地区[12]，而救护车的调度属于城市面域，所以本文对超立方模型加以改进，建立了适用于急救系统的救护车联合排队模型，并应用该模型对苏州内环线急救系统的救护车配置情况进行了分析。

1 救护车辆联合排队模型

医疗救护涉及到救护车辆配置和调度2个方面。为了清楚地说明救护车辆的运作问题，本文首先给出救护车辆的运作过程，在此基础上建立了救护车辆的联合排队模型，并给出了模型的求解算法，最后列举了关于急救系统的性能指标。

1.1救护车辆运作过程

医疗救护过程是典型的零排队容量模型，因为当一个呼叫到达系统时，其候选救护车都处于繁忙状态，该呼叫会立即转移到另外一个系统(如当地卫生院和医院分院等)，他们通常无法提供同样质量的服务。一般情况下，急救中心接到呼叫后记录具体地点，根据具体车辆情况就近派车，急救车抢救病人并转送至相应医院，然后返回各自基地继续待命。但是上海市、北京市的数据显示，现阶段是达不到最佳急救车配置(每5万人1辆急救车)的，同时呼叫中往往有许多非紧急和无效电话，约占40%，这使得高效的急救变得异常困难，很多城市开始采用带有病情优先级的急救[13]。首先接线员一般为全科医生，在接到呼叫后不仅需要确定发生地点，更重要是确定病情情况，在给予家属基本急救常识情况下，确定该呼叫优先类型，然后派车救援。下面是苏州市急救中心公布的急救过程示意图，如图2所示。

图2 苏州市急救中心救护车急救过程Fig.2 Suzhou Emergency Center ambulance emergency process

该系统可以概念化为一个空间分布多服务台(零容量)排队系统。

1.2救护车排队过程分析

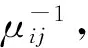
救护车仅有2种状态：繁忙或空闲，为此，定义b为一个二进制数，用bn=0表示该救护车为空闲状态，用bn=1表示该救护车为忙碌状态，对于系统中所有N辆救护车，可以用N位二进制数来表示所有N辆救护车的状态，那么N个二进制数的有序组合为B≡{bN,bN-1,…,b1}，故共有2N个状态。为了遍历救护车所有可能出现的状态空间，确保1个时间间隔内，仅能有1辆救护车响应1次紧急呼叫，或者结束1次救援，那么救护车的状态便从1(0)变为0(1)。那么对于有N辆救护车的系统而言，每个状态就可以向固有的N个状态发生变化。以3辆救护车构成的急救系统为例，则急救系统共有23=8个状态，状态组合及其转移关系如图3所示，每个状态可以向相邻的3个状态转换。如果2辆救护车状态发生改变，则必须依次进行两步转换。

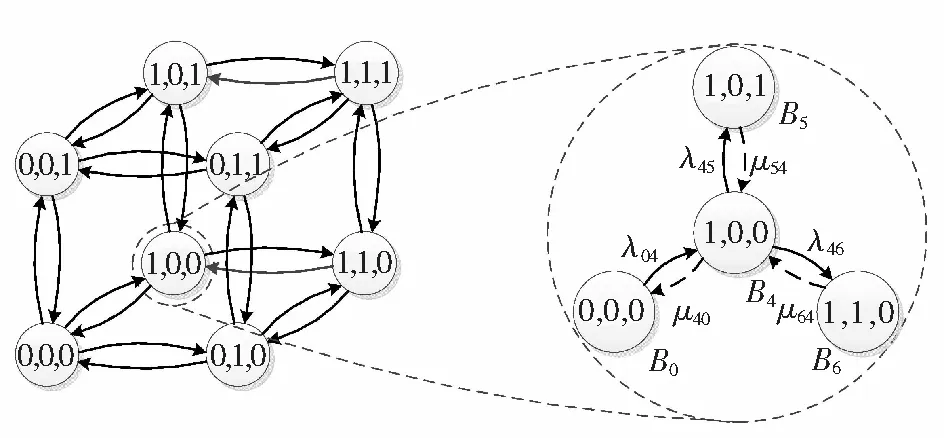
图3 急救系统车辆状态转移(以3辆车为例)Fig.3 Ambulance state transfer(taking 3 vehicles as example)

1.3状态概率求解算法

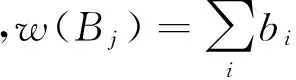
(1)

通过雅克比迭代对上述概率平衡方程中的系统救护车状态概率P{Bj}进行迭代可以获得立方体的稳态概率：

(2)

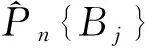
k=0,1,…,N。

(3)

且P{B0}和P{B2N-1}分别等于P(0)和P(N)，通过归纳法可以证明对于第n次迭代：

(4)

救护车状态概率的迭代过程可以先对偶数的超平面进行迭代，然后对奇数的迭代，然后再是对偶数的迭代。这样偶数、奇数交替迭代的过程为每次迭代公式(4)的计算提供了最接近未知量的估计值(这对于每个方程总是在相邻的超平面而言)，从而产生了一个渐近快于雅克比迭代的程序。

开始迭代过程时需要为奇数超平面的所有概率进行初步估计，即需要知道{Bj∈Hn:n=1,3,…}的P0{Bj}。简单起见，假设对于给定的超平面的所有状态概率是相等的，且

P0{Bj}=

(5)

把分子看作相应的M/M/N系统的适当稳态概率，分母作为二项式系数。根据上述奇偶交替的方式进行迭代，当满足收敛准则时迭代终止。除了已知的P{B0}和P{B2N-1}，其余的Pn{Bj}(j=1,2,…,2N-2)均可通过公式(2)由与Bj相邻的顶点Bi的状态概率Pn-1{Bi}线性表出，对于(2N-2个)未知量有(2N-1)个方程，可将其表示成的线性方程进行求解[14]。

本文将联合排队模型的数学语言转换成计算机语言，关键在于生成全部的救护车的状态空间、计算状态间的转移速率及概率，算法流程图见图4。

图4 算法流程图Fig.4 Flowchart of the algorithm

2 急救系统性能指标计算方法

通过求得的系统救护车状态概率，可以推算得到一系列性能指标，以对系统车辆配置情况进行评价。急救系统应确保救护车响应时间小于规定阈值，此外还要求各救护车工作强度尽量均衡。如果救护车工作强度差异较大，或各急救区域得到响应的时间差异较大，说明各区域车辆配置不科学，需要调整系统的配置方案。下面给出了部分系统性能指标的计算方法。

系统平均出行时间，表征的是救护车响应的平均行程时间，其计算思路为各救护车完成呼叫响应的平均旅行时间与对应的概率乘积之和，即

救护车工作强度ρn实质上表示救护车n处于急救状态的时间比重。该指标可衡量救护车之间工作分配是否均衡。对于工作强度特别大的车辆，可以考虑在该区域增配车辆。

救护车跨区比例，表示救护车n跨区调度概率与总调度概率之比。

地区总的跨区比例FT：一个区域无车可派时，必须要从别的区域调度车辆，急救响应时间大大增加，因此需要分析区域的跨区域比例。该指标表示区域i的救护车n响应区域j的概率和，数值越大，表示地区车辆配置越不均衡(ρnj表示派遣车辆n到区域j的概率，即车辆的工作强度)。

3 实例分析

将上述模型应用到苏州内环区域的急救系统中，输入实际调查所得数据，最终通过一系列性能指标对苏州内环区域的救护车配置情况进行评价分析。苏州市内环线包括东环、西环、南环、北环线以内地区，根据调研将该区域划分为6个急救区域，各区域的服务范围见图5。

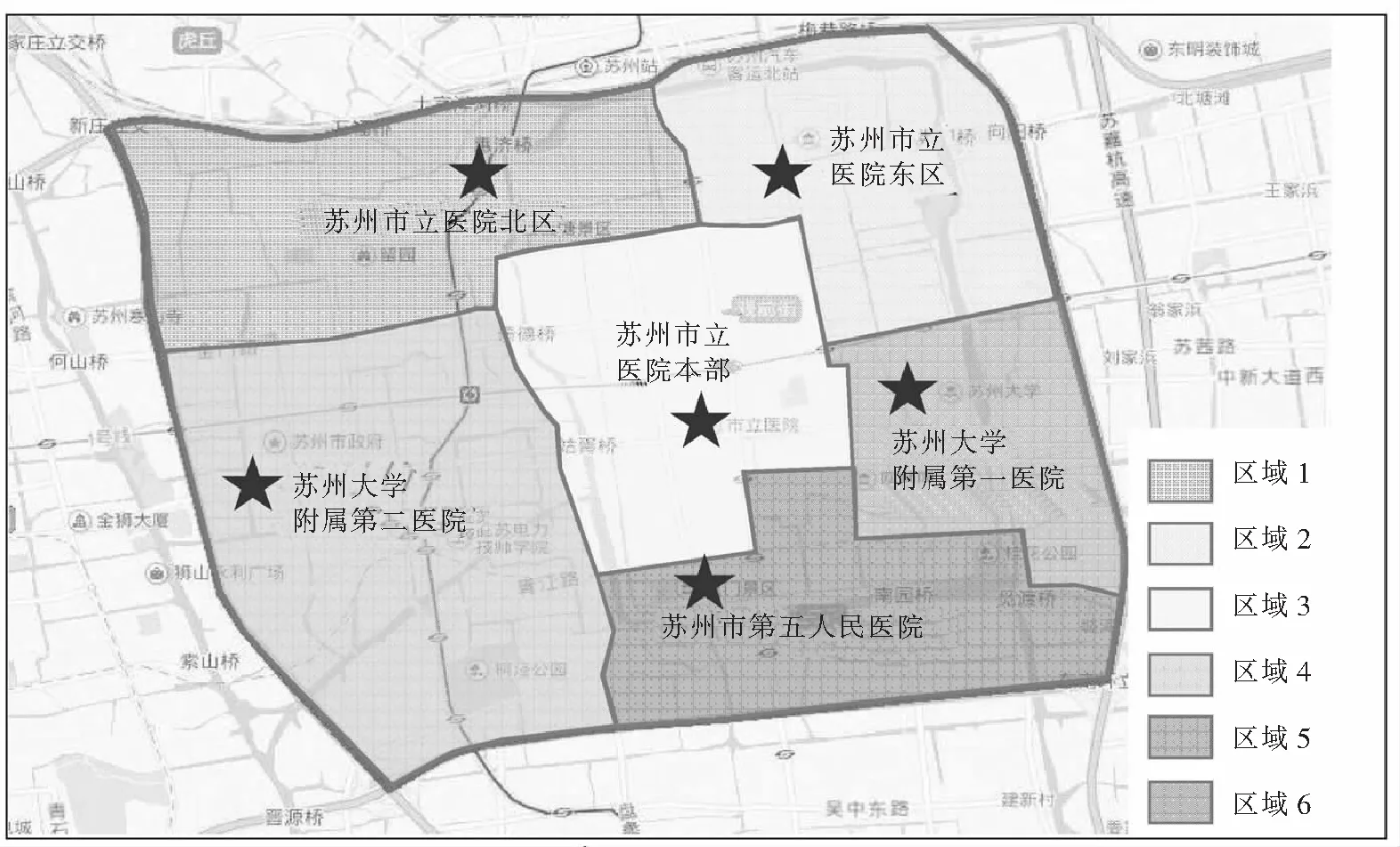
图5 案例区域划分图Fig.5 Example regional division

苏州市急救车是由苏州市急救中心统一调度的，为了获得比较可靠的信息，案例部分数据从苏州市急救中心获取，部分数据由实地调查所得。表1显示了这6个急救区域之间的时间距离(以分钟计)，该数据由百度地图测绘后，取平均值所得。

表1 各急救区域间的时间距离

根据调查数据，城区急救车辆数达到48辆，有6个急救站，即平均每个站8辆车。由于计算机能力受限，无法在6个区布置48辆车进行模拟，拟采用每个区2辆车进行模拟。表2展示的是从苏州市急救中心获取的2013年1—9月的数据，综合各月数据得到月平均电话呼入量为23 240个，由于其中有拨错、误拨电话，实际急救量约为23%，即5 427个，急救个数约1 017个。计算得到该区域平均呼叫率为λ=0.12 辆/min(由急救量计算得到)。小区工作强度是按人口数比例推导近似估计得到，见表3。

将上述数据带入模型，得到以下结果。

图6显示的是系统内12辆救护车的工作量分配情况，即每辆救护车的工作强度。显然，区域1，4，5的救护车工作强度较低，而区域3和6的救护车工作强度高达0.068，是其他区域救护车的1到3倍。说明分布在区域3和6的观前街、十全街及葑门地区的呼叫量很大，救护车繁忙程度很高，系统车辆配置不均衡，建议在这些区域增加救护车的配置。

图7给出的是各救护车辆的平均响应时间(min)，可以看出各辆救护车的平均响应时间基本在2 min左右，虽然看似相差不大，但是急救服务的响应时间对于伤病员的生命具有重要意义[15-16]。因此，对于平均响应时间相对较长的救护车所在区域建议增加救护车辆的配置数量。

表2 苏州市2013年1—9月份急救数据

表3 各区域呼叫强度

图6 救护车工作强度Fig.6 Workloads of the ambulance

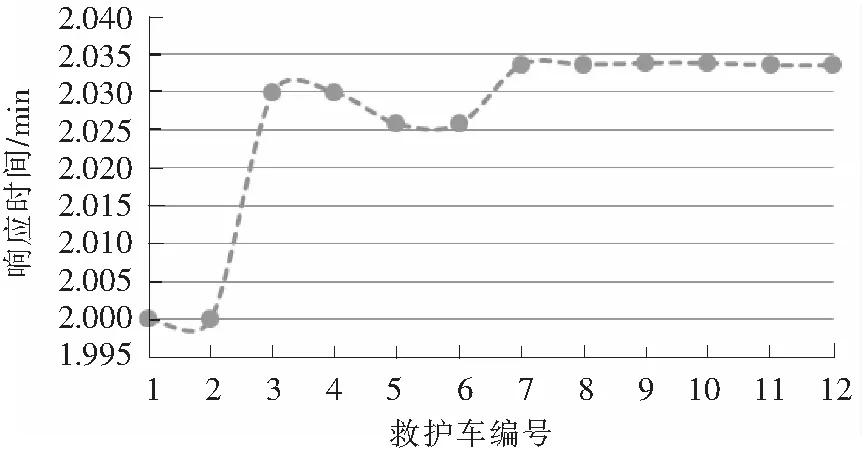
图7 救护车平均响应时间Fig.7 Mean travel time of the ambulance

图8给出的是各救护车的跨区域调度比例，该指标数值越大，反映该车被派遣到其他区域急救的概率越大，侧面说明其他区域的救护车配置不充足。从图8可以看出，除了区域1的1，2号救护车，其他的救护车跨区调度比例较大，尤其是区域6的救护车跨区比例超过了0.5%。结合图9急救区域的跨区调度比例综合分析可知，区域2到6的跨区响应需求较大，因此导致这些区域的救护车跨区比例也较大。

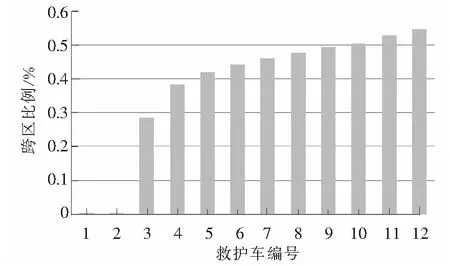
图8 救护车跨区比例Fig.8 Fractions of the interdistrict ambulances

图9 急救区域跨区比例Fig.9 Fractions of the interdistrict regions

通过以上分析可以得到结论：从多组性能指标反映的情况可知,区域2，3，6的救护车配置不论在工作强度、平均响应时间方面，还是在跨区比例方面，均暴露出这些区域救护车数量配置不足的问题，因此建议增加这几个区域急救资源配置点的救护车配置数量，从而提高苏州市内环急救系统的救援效率。

4 结 语

针对城市急救系统的运行过程，引入了超立方排队模型，建立了急救系统救护车调度问题的联合排队模型，提出了基于状态概率的求解算法，并以苏州市内环线急救系统为例，计算了急救系统的救护车工作强度、救护车平均响应时间、车辆及区域的跨区比例等性能指标。结果表明，本文的研究成果能有效地评价救护车辆的配置效果，可以为城市急救系统的救护车配置、调度等问题提供决策参考。

本文不足之处：

1)提出的模型仅能为急救系统救护车辆的配置方案进行有效评价，即对已经给定的急救系统的车辆配置方案提出合理的调整意见；

2)由于计算机容量的限制，本研究仅针对12辆救护车辆进行了实际情况的模拟分析，远少于实际的车辆配置；

3)实际中，救护车的呼叫非常频繁，往往需要同时指派多辆救护车响应呼叫，而本研究假定每次仅派出1辆救护车。

因此，未来可以开展以下研究：

1)针对急救系统的区域划分、救护车分布配置等问题，寻求最优方案；

2)改进当前算法，打破计算机容量的瓶颈，将模型应用到大容量的急救系统中；

3)考虑多辆救护车同时响应呼叫的情形，进行深入讨论。

/

:

[1] BROTCORNE L, LAPORTE G, SEMET F. Ambulance location and relocation models[J]. European Journal of Operati-onal Research, 2003, 147(3):451-463.

[2] ANDERSSON T. Decision support for operational ambulance control[C]//Management Information Systems, 2004, WIT Transactions on Information and Communication Technologies.[S.l.]:[s.n.], 2004:329-338.

[3] ANDERSSON T, VRBRAND P. Decision support tools for ambulance dispatch and relocation[J].Journal of the Operational Research Society，2007, 58:195-201.

[4] HAKIMI S L. Optimum distribution of switching centers and the absolute centers and the medians of a graph[J]. Operations Research, 1964(12)：450-459.

[5] DASKIN M S, HAGHANI A. Multiple vehicle routing and dispatching to an emergency scene[J]. Environment and Planning A, 1984, 16(10):1349-1359.

[6] TOREGAS C, SWAIN R, REVELLE C, et al. The location of emergency service facilities[J]. Operations Research, 1971, 19(6):1363-1373.

[7] LARSON R C. A hypercube queuing model for facility location and redistricting in urban emergency services[J]. Computers & Operations Research, 1974, 1(1): 67-95.

[8] LARSON R C. Urban operations research[J]. Prentice Hall-USA, 1981:559-560.

[9] JARVIS J P. Approximating the equilibrium behavior of multi-server loss systems[J]. Management Science, 1985, 31(2): 235-239.

[10] LARSON R C, MCKNEW M A. Police patrol-initiated activities within a systems queuing model[J]. Management Science, 1982, 28(7): 759-774.

[11] IANNONI A P, MORABITO R, SAYDAM C. An optimization approach for ambulance location and the districting of the response segments on highways[J]. European Journal of Operational Research, 2009, 195(2): 528-542.

[12] BURWELL T H, JARVIS J P, MCKNEW M A. Modeling co-located servers and dispatch ties in the hypercube model[J]. Computers & Operations Research, 1993, 20(2):113-119.

[13] 徐克帅, 李裕瑞. 我国农村救护车资源布局优化:以河南省郸城县为例[J]. 人文地理, 2013(1):105-109. XU Keshuai, LI Yurui. Optimization of ambulance resources in rural China: A case study of Dancheng County, Henan Province[J]. Human Geography, 2013(1): 105-109.

[14] ANDRADE L A, CUNHA C B. Decision support model to a problem of positioning bases, allocation and reallocation of ambulances in urban centers: Case study in São Paulo[J]. Transportes, 2014.

[15] 刘统新, 王政, 孙景工,等. 我国救护车应用的现状与发展分析[J]. 医疗卫生装备, 2011, 32(2):71-74. LIU Tongxin, WANG Zheng, SUN Jinggong,et al. Analysis on the present situation and development of the application of ambulance in China[J]. Medical and Health Equipment, 2011, 32(2):71-74.

[16] 刘杨，周小庄，云美萍.适于大规模网络的应急车辆配置模型[J].河北工业科技，2008，25(4)：216-218. LIU Yang,ZHOU Xiaozhuang,YUN Meiping.Emergency vehicle allocation model suitable for large-scale network[J].Hebei Journal of Industrial Science and Technology,2008,25(4):216-218.

Optimal design of ambulance vehicle configuration

FU Ziyan， ZHANG Yong

(School of Urban Railway Transportation, Soochow University, Suzhou, Jiangsu 215006, China)

The current medical emergency resource is difficult to meet the actual needs.In order to shorten the response time of emergency services and improve ambulance efficiency, rational allocation and scheduling of ambulance vehicles are necessary. This paper presents a hypercube queuing model for ambulance configuration, and based on which, gives a series of indicators to evaluate the performance of the emergency system. The algorithm is implemented by C++. Finally, the effectiveness of the model is verified by taking the emergency system of Suzhou Inner Ring as example. The results show that this study can evaluate the ambulance configuration of the emergency system, and put forward reasonable adjustment opinion, which can provide the decision basis for the ambulance configuration and dispatching of the city emergency system.

queuing theory; medical emergency resources; ambulance configuration; hypercube queuing model; C++

1008-1534(2017)05-0317-07

2017-05-23;

2017-07-05；责任编辑：冯 民

国家自然科学基金(51108289)；国家社科基金重大项目(13&ZD175)

伏紫妍(1993—)，女，江苏扬州人，硕士研究生，主要从事交通规划与管理方面的研究。

张 勇副教授。E-mail:sinkey@126.com

U121

：Adoi: 10.7535/hbgykj.2017yx05002

伏紫妍，张 勇.救护车辆配置优化设计[J].河北工业科技,2017,34(5):317-323. FU Ziyan，ZHANG Yong.Optimal design of ambulance vehicle configuration[J].Hebei Journal of Industrial Science and Technology,2017,34(5):317-323.