FRP筋混凝土梁粘结滑移力学性能数值分析*
樊 成, 李宝磊
(1. 大连大学 材料破坏力学数值实验与研究中心, 辽宁 大连 116622; 2. 中国水利水电第十三工程局有限公司 天津勘测设计研究院, 天津 300384)
FRP筋混凝土梁粘结滑移力学性能数值分析*
樊 成1, 李宝磊2
(1. 大连大学 材料破坏力学数值实验与研究中心, 辽宁 大连 116622; 2. 中国水利水电第十三工程局有限公司 天津勘测设计研究院, 天津 300384)
为了研究FRP筋与混凝土之间的粘结性能以及FRP筋与FRP筋混凝土构件的力学性能,采用ABAQUS建立FRP筋混凝土梁有限元数值模型,模型中混凝土采用塑性损伤模型,FRP筋采用线性单元.FRP筋单元和混凝土单元采用非线性弹簧单元连接,通过选取粘结滑移本构、锚固长度计算公式和调整添加弹簧的数量以及位置来考虑粘结滑移对FRP筋混凝土梁受力性能的影响.数值模拟结果与文献试验结果具有较好的一致性,验证了该有限元模型的正确性,所得结果对FRP筋混凝土结构试验具有一定的指导作用.
纤维增强复合材料; 混凝土; 粘结滑移; 锚固长度; 受力性能; 有限元; 非线性分析; 损伤模型
FRP复合材料(fiber-reinforced plastic composites,FRP)是一种多应用于建筑工程和桥梁工程的新型材料,由于其具有轻质、高强和耐腐的优点,被各国广泛应用.我国的FRP应用研究起步较晚,但发展较快,并取得了大量成果.FRP筋和混凝土之间的粘结滑移关系是分析其相互作用时需要考虑的重要因素,FRP筋与混凝土接触面的粘结强度也是影响FRP筋混凝土梁受力性能的重要因素[1].近年来,不少学者对FRP筋和混凝土之间粘结性能关系开展了一系列试验研究,建立了相对可靠的粘结滑移本构关系.葛文杰等[2]利用正截面受弯承载力计算基本假定和截面受力平衡条件,推导了FRP筋和钢筋混合配筋增强混凝土适筋梁正截面受弯承载力计算公式,根据FRP筋和钢筋的本构模型,提出了FRP筋和钢筋混合配筋增强混凝土梁两种名义配筋率和三种破坏模式的概念,并给出了三种破坏模式的判别条件;王强等[3]通过对FRP筋混凝土试件进行拉拔试验,表明随着直径与粘结长度的增大,GFRP筋与混凝土之间的粘结强度逐渐减小;王勃等[4]采用拔出试验研究了FRP筋与混凝土的粘结破坏形式;张延年等[5]通过对不同FRP筋类型、间距以及不同加固方式的FRP筋加固梁进行受剪性能试验,研究了不同参数对表面内嵌FRP筋加固梁抗剪性能的影响规律.采用试验方法研究FRP筋与混凝土粘结滑移关系固然可靠,然而试验需花费更多的人力物力,且试验往往是破坏性的,不能重复研究,因而越来越多的学者开始倾向于用数值方法进行研究.有些学者用ANSYS对其粘结滑移关系进行了数值分析,但是计算结果不够精确,且计算费时不易收敛.本文利用ABAQUS强大的非线性功能,通过在FRP筋和混凝土之间添加Spring单元实现粘结滑移,从而实现了考虑粘结滑移情况下的FRP筋混凝土梁的力学性能数值模拟分析,不仅再现了FRP筋混凝土梁粘结滑移过程,而且观察到一些试验中无法观察到的现象,结果对进一步试验具有一定的参考价值.
1 FRP筋锚固长度
为了确保FRP筋和混凝土能够共同作用承担各种应力,FRP筋需要具有一定的锚固长度.锚固长度是指使受拉钢筋达到极限抗拉强度时所需要的最小固定长度.对于受拉钢筋而言,在粘结强度与混凝土强度成正比例关系的基础上,其锚固长度表达式为
Lab=α(fy/ft)d
(1)
式中:Lab为受拉钢筋基本锚固长度;α为锚固钢筋外形系数,光面钢筋为0.16,带肋钢筋为0.14;fy为普通钢筋的抗拉强度设计值;ft为混凝土轴心抗拉强度设计值,当混凝土强度高于C60时,按C60取值;d为锚固钢筋的直径.
La=ζaLab
(2)
式中:La为受拉钢筋锚固长度;ζa为锚固长度修正系数,对于普通钢筋根据规范GB50010-2010的规定选取.
FRP筋与钢筋材料本质不同,不适合用钢筋的锚固长度公式计算FRP筋的锚固长度.FRP筋和混凝土粘结强度受FRP筋的类型和接触面特征等因素的影响,因此需要根据FRP筋与混凝土的粘结滑移本构关系确定其锚固长度[6].考虑到材料安全系数γm、位置修正系数γt、混凝土保护层修正系数γc、弹性模量修正系数γE和安全系数γg,所确定的基本锚固长度表达式为ldb=γtγclm,最小锚固长度为Ld=γgldb,其中

(3)
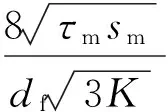
(4)
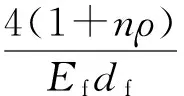
(5)
式中:τm为试验粘结应力峰值;sm为与粘结应力峰值对应的滑移量;df为FRP筋直径;n=Ef/Ec,Ef为FRP筋弹性模量,Ec为混凝土弹性模量;ρ=Af/Ac,Af为FRP筋的截面面积,Ac为混凝土的截面面积.
2 本构关系
2.1 混凝土本构关系
受压时σ-ε关系的表达式为
σ=(1-dc)Ecε
(6)
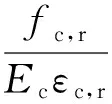
(7)
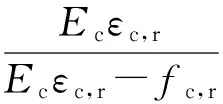
(8)
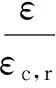
(9)
(10)
式中:fc,r为立方体抗压强度标准值;dc为混凝土塑性损伤因子;其他各参数及取值见规范GB50010-2010.
受拉时σ-ε关系的表达式[7]为
(11)
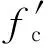
2.2 FRP筋本构关系
FRP筋应力-应变关系为σf=Efεf,如图1所示,其中,各变量含义参见规范GB50010-2010.
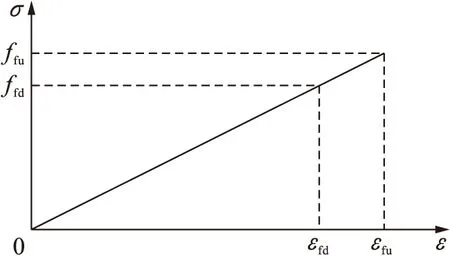
图1 FRP筋的应力-应变曲线Fig.1 Stress-strain curve of FRP bar
2.3 粘结滑移本构
对FRP筋混凝土构件进行单端拉拔试验,能够较为准确地反应FRP筋与混凝土之间的锚固滑移关系,而且还能获取很多有价值的试验数据.文献[6]通过84个FRP筋混凝土试件的拉拔试验,分析提出了FRP筋与混凝土的粘结应力-滑移量(τ-s)关系模型,表达式如下所示.
上升段:
(12)
下降段:

(13)
残余阶段:
τ=τr(s>sr)
(14)
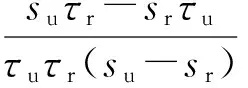
根据FRP筋锚固长度计算公式计算出FRP筋两端的锚固长度,在ABAQUS中对需要锚固部分的FRP筋采用嵌入的方式将其嵌入到混凝土梁中.对不需要进行锚固的FRP筋则需要按FRP筋与混凝土的粘结滑移本构模型添加弹簧单元.FRP筋的粘结滑移曲线如图2所示.
2.4 粘结滑移在ABAQUS中的实现
粘结滑移在ABAQUS中能否正确实现是决定可靠模拟FRP筋混凝土梁受力性能的关键因素.本文通过采用Spring2弹簧单元实现粘结滑移.Spring2单元属于非线性弹簧单元,因此不能通过Interaction模块的Special添加,只能通过对inp文件进行重新编程添加.图3为弹簧单元示意图.Spring2单元有两个节点,由于在受力过程中垂直于FRP筋两个方向的位移(y、z方向),相对于轴向位移(x方向)可以忽略不计,因此在y、z两个方向设置的弹簧单元刚度较大.沿FRP筋方向的弹簧则需要按照粘结滑移本构模型确定应力-应变的关系.添加弹簧单元时,需先将FRP筋和混凝土mesh组成具有相同节点的单元,保证FRP筋单元和混凝土单元节点一一对应且重合,然后在相对应的节点之间添加弹簧单元.在inp文件中添加弹簧的顺序是最左边的一列数字表示单元编号,从1开始依次往下排,中间和右边两列表示添加弹簧的两个节点,Wire-1表示Instance的名字.FRP筋和混凝土单元编号如图4、5所示.
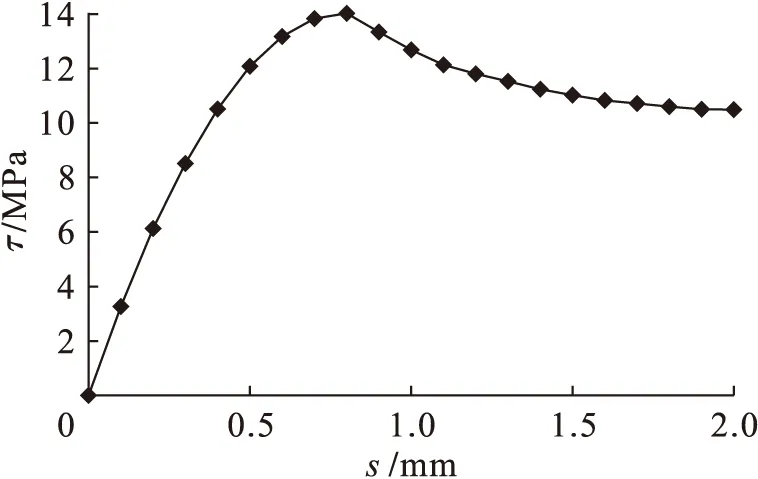
图2 FRP筋的粘结滑移曲线Fig.2 Bonding slip curve of FRP bar
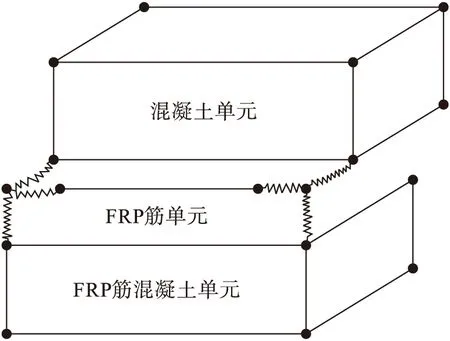
图3 弹簧单元Fig.3 Spring units

图4 FRP筋单元编号Fig.4 Unit number of FRP bars
3 算例分析
模型尺寸及力学参数[8]选择为L=1 900 mm,B=180 mm,H=250 mm,C30混凝土,fc=30.1 MPa,梁顶部配置两根直径为14 mm的受压钢筋,E=200 GPa,fu=380 MPa,μ=0.3,梁底部配置三根直径为9.5 mm的FRP受拉筋,E=72 GPa,μ=0.23,箍筋d=10 mm,fu=308 MPa.
根据算例中的材料属性和试件尺寸建立有限元模型,固定一端支座,另一支座约束y方向自由度,采用位移加载方式在1/3梁处加载,采用ABAQUS中的塑性损伤模型[9-10],为了保证计算的收敛性和计算结果的精确性,将粘滞系数设置为0.000 5,设置值过大会使得收敛较快但结果的精度会降低.考虑混凝土拉压非弹性应变的塑性损伤因子参数计算的表达式为

(15)

(16)
式中:εpl为塑性应变;bk为塑性应变与非弹性应变的比例系数.
FRP筋受力如图6所示,由图6可以看到底部的FRP受拉筋单元节点和混凝土单元节点之间添加的非线性弹簧.

图6 FRP筋受力图Fig.6 Force diagram of FRP bars
模拟计算结果如图7、8所示,可见数值计算荷载-位移曲线和试验曲线有较高的一致性,说明通过ABAQUS能够对FRP筋混凝土梁进行有限元分析,模型中参数设置是正确合理的.CFRP筋混凝土梁的曲线吻合度要比GFRP筋混凝土梁高,这是因为根据粘结滑移本构选用的锚固长度受FRP筋应力的影响,GFRP筋的应力较小,根据锚固长度公式算得的锚固长度比CFRP筋小,这就使得添加非线性弹簧的数量增多,进而导致滑移量的增加和梁承载力的下降.影响数值模拟FRP筋梁承载能力的因素还与网格划分有关,为了确保真实反映试验情况,可以将有限元模型划分的网格加密,但相应的单元、节点及需要添加非线性弹簧数也会成倍数地增加,计算工作量很大.在保证能够合理反映试验状况的情况下适当地选取划分单元的数量和添加非线性弹簧的节点是必要的,这样做不仅能够正确合理地实现数值模拟,通过模拟结果指导试验,还可以节省大量的时间从而提高效率.
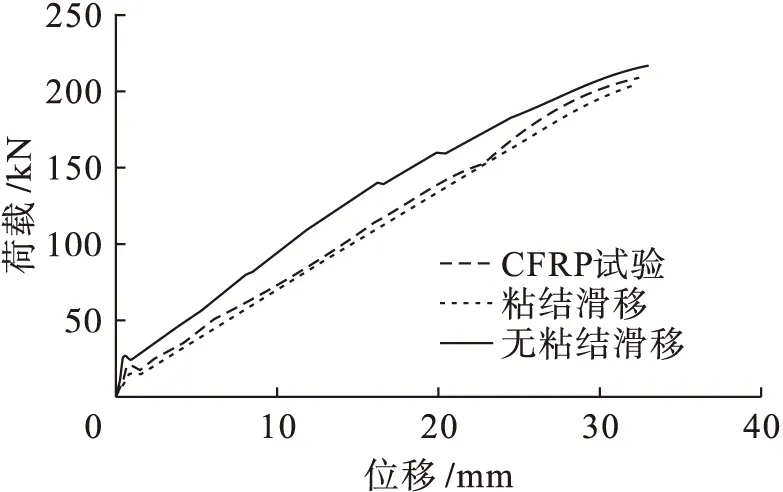
图7 CFRP筋荷载-位移曲线Fig.7 Load-displacement curves of CFRP bars
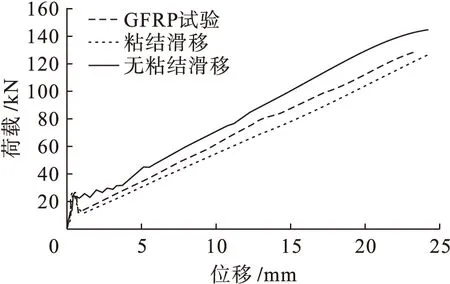
图8 GFRP筋荷载-位移曲线Fig.8 Load-displacement curves of GFRP bars
4 结 论
本文主要研究了通过ABAQUS的Spring2单元实现FRP筋与混凝土之间的粘结滑移,并通过算例与试验结果进行对比,验证了所选用的粘结滑移本构和锚固长度计算公式的正确性,模拟结果对后续FRP筋混凝土粘结滑移试验具有一定的指导作用.ABAQUS中的Spring2(非线性弹簧)单元能够模拟再现FRP筋的粘结滑移过程,计算精度可通过调整网格划分的精细度及所添加Spring2单元数的多少来控制.
FRP筋与混凝土之间的粘结滑移一定程度上受FRP筋类型的影响,鉴于本文所选取的试验算例及FRP筋类型有限,其他不同类型的FRP筋和混凝土粘结滑移关系有待进一步研究.
[1] 冯肖,葛文杰,陈坦,等.FRP筋混凝土梁研究现状 [J].新型建筑材料,2015,42(12):48-51.
(FENG Xiao,GE Wen-jie,CHEN Tan,et al.Current study status of FRP reinforced concrete beams [J].New Building Materials,2015,42(12):48-51.)
[2] 葛文杰,张继文,戴航,等.FRP筋和钢筋混合配筋增强混凝土梁受弯性能 [J].东南大学学报(自然科学版),2012,42(1):114-119.
(GE Wen-jie,ZHANG Ji-wen,DAI Hang,et al.Fle-xural behavior of concrete beam with hybrid reinforcement of FRP bars and steel bars [J].Journal of Southeast University(Natural Science Edition),2012,42(1):114-119.)
[3] 王强,金清平,姜天华.FRP筋与混凝土粘结性能试验研究 [J].建材世界,2014,35(6):44-46.
(WANG Qiang,JIN Qing-ping,JIANG Tian-hua.Experimental study of bond behaviors between FRP bars and concrete [J].The World of Building Materials,2014,35(6):44-46.)
[4] 王勃,付德成,杨艳敏,等.FRP筋与混凝土界黏结破坏性能研究 [J].混凝土,2010(3):26-28.
(WANG Bo,FU De-cheng,YANG Yan-min,et al.Experimental study on bond failure between FRP bars and concrete [J].Concrete,2010(3):26-28.)
[5] 张延年,付丽,刘新,等.表面内嵌 FRP 筋抗剪加固 T 形混凝土梁参数影响 [J].沈阳工业大学学报,2015,37(2):212-218.
(ZHANG Yan-nian,FU Li,LIU Xin,et al.Parameter influence of T shaped concrete beams shear-strengthened with NSM FRP bars [J].Journal of Shenyang University of Technology,2015,37(2):212-218.)
[6] 张海霞,朱浮声.考虑粘结滑移本构关系的FRP筋锚固长度 [J].四川建筑科学研究,2007,33(4):43-46.
(ZHANG Hai-xia,ZHU Fu-sheng.Study on the anchorage length of FRP bars with bond-slip constitutive relationship [J].Sichuan Building Science,2007,33(4):43-46.)
[7] 沈聚敏,王传志,江见鲸.钢筋混凝土有限元与板壳极限分析 [M].北京:清华大学出版社,1993.
(SHEN Ju-min,WANG Chuan-zhi,JIANG Jian-jing.Finite element method of reinforced concrete and li-mite analysis of plates and shells [M].Beijing:Tsinghua University Press,1993.)
[8] 徐新生,纪涛,郑永锋.FRP筋混凝土梁弯曲试验及设计方法探讨 [J].建筑结构,2008,38(11):45-48.
(XU Xin-sheng,JI Tao,ZHENG Yong-feng.Test and design method on flexural resistance performance of concrete beam with FRP bar [J].Building Structure,2008,38(11):45-48.)
[9] 李宝磊,宋力,樊成,等.FRP筋混凝土梁受弯性能的数值分析 [J].山西建筑,2015,41(5):22-24.
(LI Bao-lei,SONG Li,FAN Cheng,et al.Finite element analysis of the bending performance on FRP reinforced concrete beam [J].Shanxi Architecture,2015,41(5):22-24.)
[10]李宝磊,宋力,樊成,等.FRP筋混凝土梁受弯性能影响因素的有限元分析 [J].水利与建筑工程学报,2015,13(3):100-104.
(LI Bao-lei,SONG Li,FAN Cheng,et al.Finite element analysis of the bending performance influencing factors of FRP reinforced concrete beam [J].Journal of Water Resources and Architectural Engineering,2015,13(3):100-104.)
(责任编辑:钟 媛 英文审校:尹淑英)
NumericalanalysisformechanicalperformanceofbondingslipofFRPreinforcedconcretebeam
FAN Cheng1, LI Bao-lei2
(1. Research Center for Numerical Tests on Material Failure, Dalian University, Dalian 116622, China; 2. Tianjin Exploration and Research Institute, STECOL Corporation, Tianjin 300384, China)
In order to study the bonding performance between FRP bars and concrete and the mechanical properties of FRP bars and FRP reinforced concrete members, the finite element numerical model for FRP reinforced concrete beam was established with ABAQUS. In the model, the plastic damage model was adopted for the concrete, and the linear unit was adopted for the FRP bars. The FRP bar units and concrete units were linked through nonlinear spring units. Through choosing the bonding slip constitutive relationship and the computational formula of anchorage length as well as adjusting the number and position of added springs, the effect of bonding slip on the mechanical performance of FRP reinforced concrete beam was considered. The numerical simulation results are very consistent with the experimental results in the literatures, and the correctness of the proposed finite element model gets verified. Furthermore, the numerical results have a certain guiding role in the experiments of FRP reinforced concrete structures.
fiber-reinforced composite; concrete; bonding slip; anchorage length; mechanical performance; finite element; nonlinear analysis; damage model
TU 352
: A
: 1000-1646(2017)05-0596-05
2016-09-01.
辽宁省自然科学基金资助项目(2015020222).
樊 成(1976-),男,河北泊头人,副教授,博士,主要从事岩石与混凝土结构损伤破坏的数值与试验等方面的研究.
* 本文已于2017-01-19 18∶00在中国知网优先数字出版. 网络出版地址: http:∥www.cnki.net/kcms/detail/21.1189.T.20170119.1800.026.html
10.7688/j.issn.1000-1646.2017.05.22

