瞬态力-热耦合作用下水泥环形态对套管应力的影响

席岩，李军，柳贡慧，2，查春青，秦曦，严攀

（1.中国石油大学（北京）石油工程学院，北京 102249；2.北京工业大学，北京 100124；3.中国石油天然气集团公司西部钻探工程技术有限公司，新疆 鄯善 838200）

瞬态力-热耦合作用下水泥环形态对套管应力的影响

席岩1，李军1，柳贡慧1，2，查春青1，秦曦3，严攀1

（1.中国石油大学（北京）石油工程学院，北京 102249；2.北京工业大学，北京 100124；3.中国石油天然气集团公司西部钻探工程技术有限公司，新疆 鄯善 838200）

基于页岩气水平井压裂工程实际，采用解析法与数值法结合的方式，建立了压裂过程中井筒温度场计算模型和套管偏心、水泥环缺失有限元模型，据此研究瞬态力-热耦合作用下的水泥环形态对套管应力的影响。结果显示：1）页岩气井压裂过程中瞬态力-热耦合作用显著提高了套管应力；套管应力呈先升高后降低的动态变化，最大应力值出现在压裂初期。2）水泥环完整或套管偏心时，瞬态力-热耦合作用降低了套管应力周向分布不均匀差异；水泥环缺失时，套管应力随着缺失角、偏心距的增大而提高。研究结果对于精确计算页岩气井压裂过程中的套管应力具有重要意义。

页岩气井；套管变形；井筒温度场；瞬态温度力-热耦合；水泥环形态

0 引言

页岩气水平井固井水泥环形态多变［1-3］，压裂过程中套管易出现应力集中；同时由于体积压裂压力高、排量大、时间长，力-热耦合作用对套管应力影响明显［4-8］。国外学者研究表明，页岩气井压裂过程中井筒温度变化是套损问题出现的重要原因［9-10］。国内学者就压裂过程中水泥环完整时稳态温度变化对井筒完整性的影响进行了分析，但未考虑压裂过程中瞬态力-热耦合作用下水泥环形态对套管应力大小、分布的影响［11-12］。四川威远-长宁页岩气套损问题频发［13-15］，且多个套损点出现在套管变形、水泥环缺失处，因此，明确瞬态力-热耦合作用下水泥环形态对套管应力的影响，对精确计算套管应力、提升井筒完整性具有重要意义。

本文基于页岩气井压裂工程实际以及套后成像测井资料，建立了井筒温度场模型和套管-水泥环-地层组合体有限元模型，采用解析法和数值法结合的方式，计算瞬态力-热耦合作用下套管应力变化，并分析了水泥环形态对套管应力的影响规律。研究结果可为页岩气水平井压裂过程中套损问题的分析提供参考。

1 压裂过程中温度场计算模型

设定地层温度与深度呈线性关系：

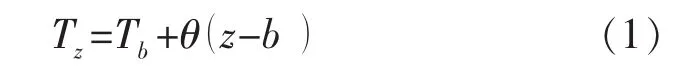
式中：Tz为地层某一点的温度，℃；Tb为地层恒温点的温度，℃；θ为地温梯度，℃/m；z为地层某一点的深度，m；b为基准深度，m。

基于能量守恒方程建立井筒温度场模型。沿井筒轴向将井筒划分j等分，沿井壁到地层无限远处划分为i个区域。井筒内流体的能量守恒方程为

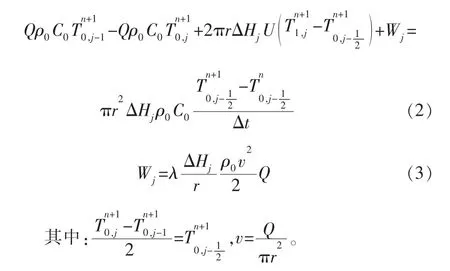
式中：Q为压裂液排量，m3/min；ρ为密度，kg/m3；C为质量热容，J/（kg·℃）；r为套管内径，m；ΔHj为单元体高度，m；U为流体与套管表面对流换热系数，W/（m2·℃）；λ为套管摩阻系数（与流体雷诺数有关）；v为套管内流体流速，m/s；Wj为压裂液与井壁接触摩擦产生的热量，J；T为温度，°C；Δt为时间差，s；下标0代表压井液。

与流体接触的套管单元的能量守恒方程为

式中：K为压裂液导热系数，W/（m·℃）。

其余固体单元的能量守恒方程为

根据网格划分情况，i=0，1≤i＜n，n≤i＜m，m≤i＜k（n，m，k分别代表划分的网格数）时，ρ，C，K分别代表压裂液、套管、水泥环、地层的密度、质量热容和导热系数。

根据雷诺数计算可得，套管压裂时井筒内压裂液流态为紊流。其换热系数计算公式为

张绍凡就是我的天敌，这丫头片子从小就看不起我。虽然我们住在同一条街道，年纪相仿，从上幼儿园开始就是同学，但她一直都是老师宠爱、同学拥护的好班长。而我，却是大家眼中吊儿郎当、不学无术，还总调皮捣乱的坏孩子。

紊流状态下的斯坦顿数计算公式为

式中：St为斯坦顿数；Re为雷洛数；Pr为普朗特数；γ为压裂液表观黏度，Pa·s。

根据式（1）—（8），计算可得压裂过程中压裂液沿井筒的温度变化，并且可以计算出不同排量下水平段任意位置流经该处的随时间变化的压裂液温度，将其作为条件参数输入到有限元模型中，实现解析法和数值法结合。

式中：l为井眼水平段某处到趾端的距离，m。

2 数值模型的建立

2.1 模型建立

假定套管、水泥环、地层在水平方向上热力学性质保持不变，相关问题转化为平面热传导和应力、应变问题。如图1所示，选择距离趾端为l的组合体截面作为研究对象，经过该截面的压裂液温度为，建立3 m×3 m的基础有限元模型，采用变密度网格划分方式以减小计算干扰。在基础有限元模型上改变水泥环形态（见图2。其中：SH为最大水平地应力；SV为垂向地应力；△为偏心距；α为缺失角；δ为偏心角）。

在载荷施加和边界条件设置方面，采用有限软件Abaqus中的Predefined功能施加地应力，套管内壁加入液压。温度内边界为动态边界条件，作为随时间变化的动态函数输入有限元模型中；温度外边界为地层边界，设置为稳定热源。X，Y方向模型边界位移为0。

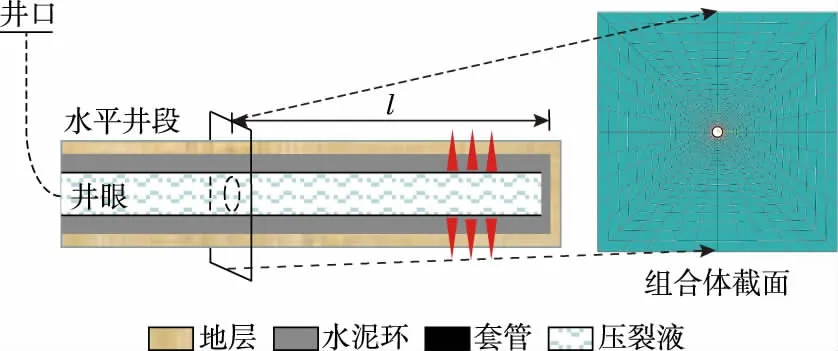
图1 基础数值模型

图2 套管偏心、水泥环缺失数值模型

2.2 参数设置

参数设置以页岩气井W1井工程实际参数为准，具体见表1。

W1井井深为2909 m，垂深为1745 m，井底温度为78.5℃，压裂液初始温度为20℃，压裂泵压为60MPa，排量为16 m3/min，压裂时间为4 h。套管壁厚为9.17mm，钢级为TP95。地层最大水平、垂向主应力分别为48，35MPa。因套后测井资料显示水泥环缺失处为液相物质，为简化计算，假设水泥环缺失处填充物为水，其热膨胀系数ξ（T）为随温度变化的变值。

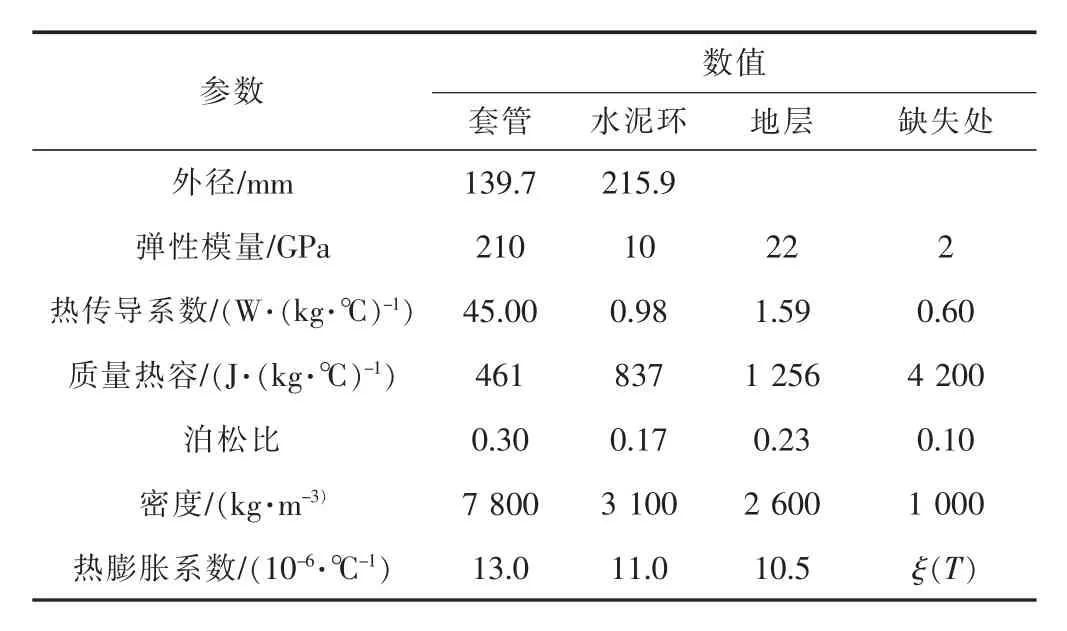
表1 套管、水泥环、地层几何及力学参数

3 水泥环形态对套管应力影响分析

3.1 压裂过程中压裂液温度的计算

压裂过程中，压裂液温度与压裂排量、时间有关。选择压裂排量8，12，20 m3/min作为参考。选取跟端处即水平段距离趾端lmax处为研究对象，计算该处压裂液温度瞬态变化（见图3）。

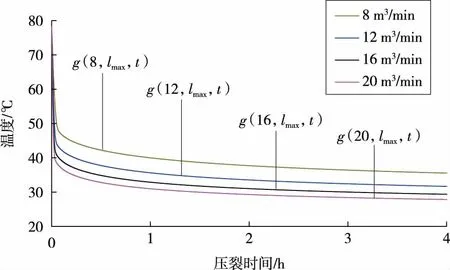
图3 不同排量下跟端压裂液温度随时间变化

由图3可知：跟端压裂液初始温度为储层温度，压裂过程中温度先快速后缓慢下降；排量不同时，相同时刻排量越大，温度越低，降幅不断减小。将温度-时间瞬态变化数据输入到有限元软件中进行下一步计算。

3.2 水泥环形态对套管应力的影响

3.2.1 完整水泥环形态时

瞬态力-热耦合作用改变了套管应力大小（见图4）。不考虑力-热耦合作用时，压裂过程中套管应力为恒值；考虑该作用时，套管最大应力先迅速升高，然后缓慢下降。这主要是因为：压裂初期，井筒内液体与套管内壁直接接触，套管内壁遇冷剧烈收缩，外壁则来不及冷却而变形，在整体几何条件约束下，由于变形不协调而形成了对内壁收缩的抵制，导致套管内壁承受巨大拉应力，外壁受压，因此最大应力（位于内壁）迅速提升；压裂一段时间后，套管冷却速度稳定，外壁开始冷却且收缩趋势增强，内部收缩趋势减弱，内拉外压作用减弱，从而使得套管最大应力逐渐降低。套管最大应力值出现在t1=0.13 h（485 s）。

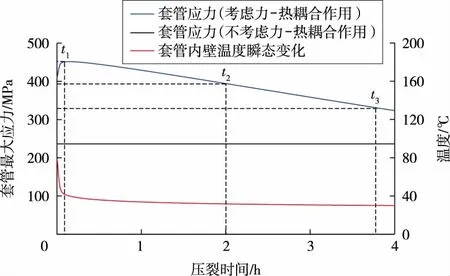
图4 力-热耦合作用下套管最大应力瞬态变化

力-热耦合作用改变了套管应力分布（见图5）。选择t1，t2，t3时刻，对比不同时刻下内壁应力周向分布。不考虑力-热耦合作用时，受非均匀地应力影响，套管应力周向分布具有明显非均匀性，水平方向上受力最大，垂直方向上受力最小；考虑力-热耦合作用时，套管内壁周向分布应力整体大幅提升，但是周向上分布的应力非均匀差异变小。

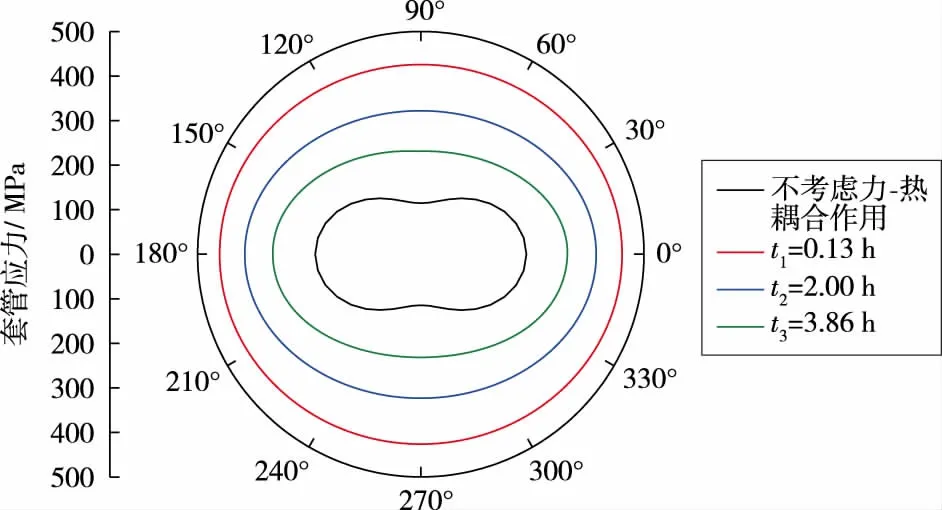
图5 不同时刻套管内壁应力大小及分布

3.2.2 套管偏心时

页岩气井水平段达到千米以上，导致套管居中难以保证。套管成像测井表明，部分页岩气井套损点处偏心明显。考虑瞬态力-热耦合作用时，不同时刻套管应力不同。本文选择应力最大值出现时刻进行研究。图6为力-热耦合作用下偏心时套管应力周向分布曲线。由图可知：不考虑力-热耦合作用（No），套管偏心时最大应力要比无偏心时大，应力周向分布差异明显；考虑力-热耦合作用（Yes），套管应力整体显著提高，周向不同位置处应力差异变小。其规律是：偏心角为0°时，套管最大应力随着偏心距的增大而提高；偏心距为30mm时，套管最大应力随着偏心角的增大而降低。

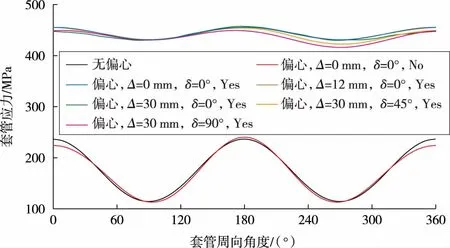
图6 力-热耦合作用下偏心时套管应力周向分布

3.2.3 水泥环缺失时

偏心导致固井过程中水泥浆周向流速分布不均，窄间隙处剖面顶替效率急剧下降，易导致窜槽发生。套后成像测井表明，套损点处偏心较为严重，伴随有明显连续窜槽，充填物质为液相，压裂过程中易产生应力集中。取偏心角为0°作为基础计算条件，建立偏心、窜槽共存有限元模型进行计算。图7为力-热耦合作用下水泥环缺失时套管应力周向分布。由图7可知：不考虑力-热耦合作用（No）时，套管应力在水泥环缺失位置中部明显提升；考虑力-热耦合作用（Yes）时，套管最大应力位置出现在缺失位置的两侧，提升幅值更大。其规律是：偏心距为0时，缺失角增大，套管最大应力值不断提高；缺失角为30°时，偏心距不断增大，套管最大应力值不断提高。

图7 力-热耦合作用下水泥环缺失时套管应力周向分布

综上所述，在一定井筒力学条件和压裂工况下，套管内壁最大应力出现在压裂初期0.13 h。完整水泥环状态、考虑力-热耦合作用时，套管最大应力为452.4MPa，相比较不考虑力-热耦合作用提高91.2%；偏心角为0°、缺失角为90°、考虑力-热耦合作用时，套管最大应力为625.4MPa，相比较不考虑力-热耦合作用、完整水泥环形态时提高164.3%，已经接近套管屈服强度655MPa，套管损坏风险大幅提高。

4 结论

1）考虑套管对流换热系数随排量变化以及摩擦生热，建立了压裂过程中井筒温度场模型，计算了压裂液温度瞬态变化。结果表明，同位置、同时刻排量越大，压裂液温度越低。

2）建立了井筒组合体数值模型，计算了瞬态力-热耦合作用下水泥环形态对套管应力影响。结果表明：压裂过程中，套管应力先上升后下降，应力最大值出现在压裂开始初期；考虑瞬态力-热耦合作用时，套管最大应力显著提升，套损风险大幅提高。

3）瞬态力-热耦合作用改变了套管应力分布。水泥环完整和套管偏心时，力-热耦合作用降低了周向分布不均匀差异；水泥环缺失时，力-热耦合作用使得套管最大应力出现在缺失处两侧，且随着偏心距和缺失角的不断增大，应力不断提高。

［1］刘伟，陶谦，丁士东.页岩气水平井固井技术难点分析与对策［J］.石油钻采工艺，2012，34（3）：40-43.

［2］李伟，王涛，王秀玲，等.陆相页岩气水平井固井技术：以延长石油延安国家级陆相页岩气示范区为例［J］.天然气工业，2014，34（12）：106-112.

［3］赵常青，冯斌，刘世彬，等.四川盆地页岩气井水平段的固井实践［J］.天然气工业，2012，32（9）：61-65.

［4］WOOLEY G R.Computing downhole temperatures in circulation， injection，andproductionwells［J］.Geothermics，1981，10（2）：95-102.

［5］高孝巧，杨浩，熊繁升，等.油页岩原位加热井下温度场及热应力研究［J］.断块油气田，2014，21（3）：373-377.

［6］Jr，RAMER J J.Wellbore heat transmission［J］.Journal of Petroleum Technology，1962，14（4）：427-435.

［7］王鸿勋，李平.水力压裂过程中井筒温度的数值计算方法［J］.石油学报，1987，8（2）：91-99.

［8］尹虎，张韵洋.温度作用影响套管抗挤强度的定量评价方法：以页岩水平井大型压裂施工为例［J］.天然气工业，2016，36（4）：73-77.

［9］SHEN Z，LING K.Maintaining horizontal well stability during shale gas development［R］.SPE 164037，2013.

［10］LAST N C，MUJICA S，PATTILLO P D，et al.Evaluation，impact，and management of casing deformation caused by tectonic forces in the andean foothills，colombia［J］.SPE Drilling&Completion，2006，21（2）：116-124.

［11］田中兰，石林，乔磊.页岩气水平井井筒完整性问题及对策［J］.天然气工业，2015，35（9）：70-77.

［12］刘奎，王宴滨，高德利，等.页岩气水平井压裂对井筒完整性的影响［J］.石油学报，2016，37（3）：406-414.

［13］LIAN Z H，YU H，LIN T J，et al.A study on casing deformation failure during multi-stage hydraulic fracturing for the stimulated reservoir volume of horizontal shale wells［J］.Journal of Natural Gas Science and Engineering，2015，23：538-546.

［14］戴强.页岩气井完井改造期间生产套管损坏原因初探［J］.钻采工艺，2015，38（3）：22-25.

［15］蒋可，李黔，陈远林，等.页岩气水平井固井质量对套管损怀的影响［J］.天然气工业，2015，35（12）：77-82.

［16］董文涛，申瑞臣，梁奇敏，等.体积压裂套管温度应力计算分析［J］.断块油气田，2016，23（5）：673-675.

（编辑 李宗华）

Impact analysis of cement sheath shape on casing stress under transient mechanical-thermal coupling effect

XI Yan1,LI Jun1,LIU Gonghui1，2,ZHA Chunqing1,QIN Xi3,YAN Pan1
(1.College of Petroleum Engineering,China University of Petroleum,Beijing 102249,China;2.Beijing University of Technology, Beijing 100124,China;3.West Drilling Engineering Co.Ltd.,CNPC,Shanshan 838200,China)

On the basis of fracturing engineering practice of shale gas wells,wellbore temperature field model and casing eccentricity and cement sheath deficiency finite element models were established by analytical and numerical methods,and the influence of transient mechanical-thermal coupling effect on casing stress was analyzed.The results show that:(1)the coupled mechanical-thermal effect on casing stress is significant,casing stress first increases and then decreases,the maximum casing stress appears at the beginning of fracturing.(2)when the cement sheath shape is integrity or casing is eccentric,the coupled mechanicalthermal effect reduces the difference of the stress along circumference,and when there is deficiency in cement sheath,with the increase of the eccentric distance or deficiency angle,the maximum stress of casing increases.The research results provide a reference for the accurate calculation of casing stress during fracturing in shale gas well.

shalegaswell;casingdeformation;wellboretemperaturefield;transientmechanical-thermalcoupling;cementsheathshape

TE256

A

国家自然科学基金项目“长水平段非均质页岩储层非均匀分簇射孔优化研究”（51674272）；中国石油西南油气田分公司项目“四川盆地高温高压含硫井超深井钻井、完井及试油技术研究与应用”（2016E-0608）

10.6056/dkyqt201705023

2017-02-23；改回日期：2017-07-06。

席岩，男，1985年生，在读博士研究生，从事岩石力学、井筒完整性方面的研究。E-mail：315791585@qq.com。

席岩，李军，柳贡慧，等.瞬态力-热耦合作用下水泥环形态对套管应力的影响［J］.断块油气田，2017，24（5）：700-704.

XI Yan，LI Jun，LIU Gonghui，et al.Impact analysis of cement sheath shape on casing stress under transient mechanical-thermal coupling effect［J］.Fault-Block Oil&Gas Field，2017，24（5）：700-704.