基于相关向量机模型的用电需求预测研究——以北京为例

张斌儒,唐玉萍,胡 蓉

(四川文理学院数学学院,四川达州635000)

基于相关向量机模型的用电需求预测研究
——以北京为例

张斌儒,唐玉萍,胡 蓉

(四川文理学院数学学院,四川达州635000)

用电需求的科学预测在能源系统的运行、管理与决策中起着重要的作用.针对用电需求的非线性特征及传统预测技术的缺陷,引入相关向量机构建预测模型对北京用电量进行预测.实证结果表明,与基准模型相比,所引入方法能有效提高模型预测精度,预测结果可为相关部门的决策制定提供必要的参考.

相关向量机;用电需求;支持向量回归;预测精度

0 引言

电力对国民经济的发展有着非常重要的影响,对用电量需求预测的精确性能促进能源等管理部门的科学决策,避免不必要的资源浪费.然而,已有文献预测集中在以日度或周度为频率的短期预测.[1]从管理角度看,更长时域的预测仍具有重要的现实意义.由于受经济发展的不平衡性等因素的影响,用电需求常表现出明显的非线性特征,传统的线性预测技术无法对其充分的拟合.因此,有必要开发新的预测技术以更好的模拟用电量需求的特征.

人工神经网络(Artificial Neural Networks, ANN)具备良好的非线性预测能力,该技术已被成功应用于短期电力需求预测.[2－3]研究表明,相对于基准模型,ANN能有效提高预测精度.然而,该方法易陷入局部最优、要求数据样本容量较大以及训练过程较为复杂.[4]支持向量回归(support vector regression,SVR)算法能有效克服ANN的缺陷.[5]比如,应剑烈等(2007)提出改进的SVR对电力系统短期负荷进行预测.[6]研究表明与ANN等方法相比,SVR具有良好的泛化能力,能够有效解决小样本非线性预测问题.但SVR的自由参数对预测精度影响较大,没有统一的方法对其参数进行优化;SVR的核函数必须满足Mercer’s条件以及训练过程较为复杂等.[5]

为克服SVR模型的局限,Tipping(2001, 2004)分别提出相关向量机(Relevance Vector Machine,RVM)及其改进的算法,[7－8]该算法的训练是在贝叶斯框架下进行,在先验参数的结构下基于主动相关决策理论来移除不相关的点,以保证获得稀疏化的模型.RVM的优点是能得到概率输出,训练过程简单,所选核函数不必满足Mercer条件,而且不需要太多的样本数据构造模型.该算法在电力预测领域应用较少,刘遵雄等(2004)利用RVM对电力负荷进行了实证研究,[9]取得了较好的预测效果,但在用电需求方面的预测效力仍需进一步检验.

利用2010年1月至2017年2月北京用电量数据,引入RVM模型对北京月度用电量进行为期12个月的预测,SVR以及ANN作为基准模型用于预测对比.

1 预测方法构建

1.1 相关向量机算法原理

RVM是Tipping在2001年提出的一种稀疏概率模型,[7－8]其基本原理概括如下:

其中w＝[w0,w1,...,wN]Τ表示权重向量, ε为服从均值为零,方差为σ2的高斯分布,方差由数据进行估计.Φ为N×(N＋1)矩阵且Φnm＝K(xn,xm－1)表示核函数,Φn1＝1.从(1)式可以看出,模型的输出可以表示为非线性函数的加权组合,且核函数不必满足Mercer条件.因此,数据集t＝(t1,t2,...,tN)Τ的似然函数可以表示为:

若不对权值进行约束,直接求解(2)式可能会导致模型过度学习问题.因此,根据稀疏贝叶斯方法对w定义为均值为0的高斯先验分布:

其中,α＝[α0,...,αN]Τ为包含N＋1个超参数的超参数向量,而每个独立超参数控制权参数的先验分布,从而导致RVM预测模型的稀疏性.

利用贝叶斯原理求出未知权参数向量w的后验分布:

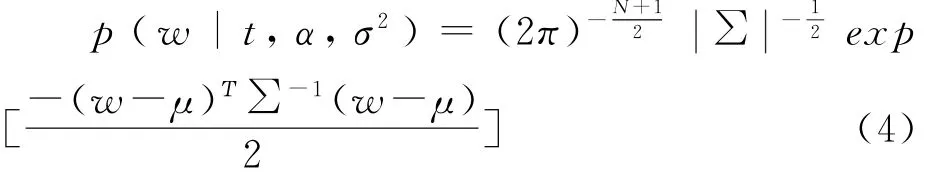
其中,∑＝(σ－2ΦΤΦ＋A)－1和μ＝σ－2∑ΦΤt分别表示后验权重协方差矩阵和后验均值,A＝diag(α0,...,αN).

最优估计值αMP可以通过构造如下极大似然估计的对数形式进行估计:

然后,最优估计值μMP可以通过μ＝σ－2∑ ΦΤt获得.最终,预测输出表达式为:y＝ΦμMP.

在整个优化算法中,μMP中包含大多数零元素,而μMP用于对权重向量的估计.因此,与SVR算法的支持向量类似,被估计的权重向量中的非零元素被当作相关向量用于模型的预测.[7－9]在预测表达式中,核函数需要用户自行确定.

1.2 混合核函数的构造与自由参数的优化

由于RVM模型的核函数不必满足Mercer定理,因此对其选择相对自由.而混合核函数的本质是将若干个核函数进行线性组合从而聚合并且反映不同的核函数的特征性质.本文将利用高斯径向基函数(RBF)以及多项式函数进行线性组合以构造RVM类预测模型的混合核函数:

其中,参数η∈[0,1]为核函数的权重系数.在SVR算法中给定RBF核函数,有三个自由参数(和核宽度)需要优化,实质上是求解一个三维优化问题.而RVM算法中有两个参数δ和η需要优化,蝙蝠算法(Bat Algorithm,AB)在对模型参数优化中表现出实用性和优异性能,[10]能有效避免PSO以及GA等传统优化算法的缺陷,故本文采用BA对所有预测模型的自由参数进行优化选择.

1.3 预测程序

根据RVM以及BA优化算法原理,[10]具体预测程序概括如下:

步骤1:预设参数.在利用BA进行参数优化前,需对该算法本身的一些参数进行预设.本文运用Taguchi法(Ghani,2004)对BA的参数进行设置.[11]

步骤2:初始化参数.为了得到最优的RVM参数集,需对蝙蝠种群进行初始化,因为σ2和超参数α通过迭代进行计算,这里也需事对其初始值设置.具体而言,RVM的两个参数(δ和η)需要通过BA进行优化,因此实质上是求解一个二维优化问题.

步骤3:产生新解.蝙蝠将依据自身所处的位置以及速度迭代进行计算以获取最优的参数.

步骤4:评估适应度.本文采用均方误差(Mean Square Error,MSE)作为适应度函数以评估模型的预测性能.MSE旨在度量预测值与实际值之间的偏离程度,该值越小,意味着模型预测精度越高.

步骤5:停止准则.步骤3与4循环迭代进行,直到进化代数达到用户规定的值为止,并且在该点适应度函数曲线收敛.此时得到最优的RVM参数集.

步骤6:获得模型的最优参数集后,在训练集上训练得到RVM模型,然后在测试集上进行预测实验得到预测值.

2 实证检验

2.1 数据描述与模型输入集构造

作为应用,本文以北京为例,对其月度用电需求进行预测.用电量月度数据来源于金融数据库万得(Wind)资讯,数据收集的时间跨度为2010年1月至2017年2月.

北京是全国的政治与文化中心,用电量需求增长较快且波动明显,是一个复杂的非线性系统,且受季节性的影响较大,在每年的7、8月份以及12月到次年的1月出现用电量高峰.因此,本文引入季节性虚拟变量D以进行季节调整,当某月为用电高峰期时,取值为1,否则为零.由于受经济一体化以及区位因素的影响,天津与北京用电需求时间序列之间具有相似的波动特征.交叉相关分析结果显示,北京用电量(yt)与自身12阶滞后变量(yt－12)之间的最大相关系数为0.9089且显著,与天津用电量(x)的滞后12期时间序列(xt－12)之间的最大相关系数为0.8470且显著,因此,它们均被选为预测变量.

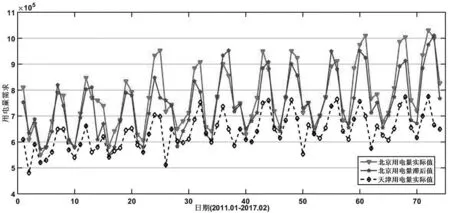
图1 各个变量趋势图

图1直观展示了北京用电需求与自身滞后观测以及天津用电需求之间的趋势,可以看出三个变量之间具有一致的波动特征和趋势性.因此,本文认为所选预测变量对北京用电需求具有很好的预测作用.

根据以上分析,将RVM模型的输入集表示为:{yt－12,xt－12,D},输出变量为用电需求yt.基于滞后阶数进行对齐后的实验数据集共74个数据点.将实验数据分成训练集(前62个月)与检验集(后12个点)两部分分别用于训练模型和预测检验.

2.2 结果与讨论

平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)、均方根误差(Root Mean Square Error,RMSE)和相关系数三个统计指标被用于预测性能度量,MAPE和RMSE衡量预测值与实际值之间的偏离程度,该值越小表明预测性能越强,而R度量实际值与预测值之间的相关程度,该值越接近1表明模型拟合程度越高.

预测之前,需在训练集上获得最优参数以构造预测模型.对RVM模型,核宽度σ和权重系数η需要设置,本文采用BA对其进行优化,目标是使得适应度函数(均方误差)值最小.对SVR模型,仍然使用该优化算法对其参数进行优化.RVM的最优核宽度σ＝0.770,η＝0.446,相关向量占训练样本的比例为15.1%.SVR的三个最优参数为:C＝28.34,ε＝0.09,σ＝2.07,支持向量占比则为76.2%.可以看出,RVM能提供更稀疏的解.ANN模型的基本结构为:隐藏层数为1,输入层节点为数目为3,输出层节点数为1.预测结果见表1,其中加黑字体表示与实际值偏离最小的预测值.

表1 不同模型预测结果对比

表1显示3个模型中RVM预测结果最好,最佳预测值为6个,而SVR为4个,ANN表现最差,预测最佳值仅占1个月.图2更为直观的呈现了三个预测模型的预测曲线,可以看出本文所引入的RVM模型具有更强的拟合能力,SVR也具有较强的非线性拟合效果,而ANN的预测曲线偏离最大.

基于预测结果的三个统计指标值见表2.该表显示,整体而言,对于三个统计指标,训练集上的值要优于测试集上的值.具体而言,在测试集上RVM与SVR的值明显优于ANN模型,但RVM表现最好;MAPE和RMSE值意味着RVM的预测值与实际值之间的偏离最小,R值暗示所引入模型的拟合值与实际值之间具有最大相关性.因为SVR具有良好的小样本非线性预测能力,其预测性能仅次于RVM模型,而由于ANN对样本容量要求较高,因而预测效果相对较差.最后,运用paired－t检验对三个模型的预测误差(相对误差)进行显著性检验,结果显示RVM与SVR之间的预测精度没有显著性差异,但与ANN之间在5%水平具有显著性差异,这进一步验证了所引入预测方法的有效性.

图2 不同模型预测曲线对比

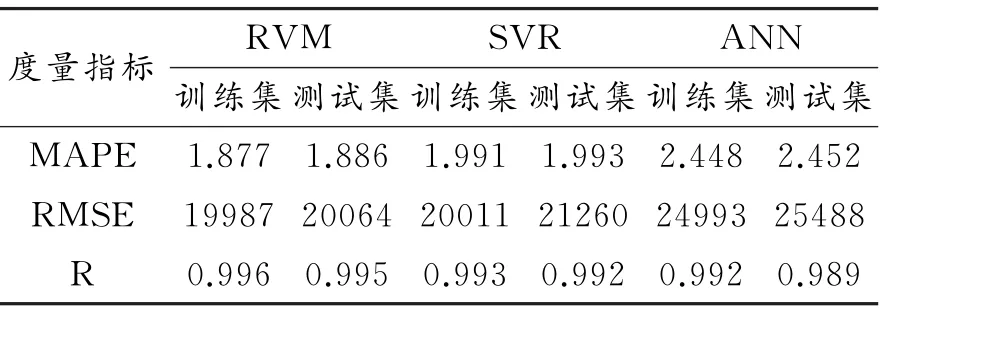
表2 各个模型在训练集与测试集上的性能指标值对比

3 结论与展望

准确预测用电量需求对能源体系的科学决策至关重要.针对传统预测技术不适用于小样本非线性预测系统,本文引入RVM模型对北京用电量进行了预测.实证结果显示,与基准模型SVR以及ANN相比,RVM预测精度最高,证实了RVM为一种有效的预测工具.

相对于基准模型,RVM算法训练过程简单,适合于小样本非线性预测问题.SVM预测效果也较为理想,但受限于模型自由参数的选择,使得训练过程较为复杂.而ANN对数据样本容量要求较高,训练时间较长,容易出现过拟合等现象,这使得预测效果相对较差.本文预测方法可扩展到其它社会经济预测领域,比如,可考虑将该方法应用于四川省九寨沟景区并对其游客流量进行预测研究.

研究所引入模型的预测结果可为能源体系的运行与管理提供必要的参考.探索更具预测能力的影响因素作为模型的输入集以进一步提高模型预测精度是将来努力的方向.

[1]McDonald,J R.The forecasting of growth of demand for electrical energy[M].In Modern Power System Planning.Wang X,McDonald JR(eds),McGraw－Hill Book Company:New York,1994:43.

[2]Abdel－Aal,R E.Short－term hourly load forecasting using abductive networks[J].IEEE Transactions on Power Systems,2004(1):164－173.

[3]Darbellay,G A.,Slama M.Forecasting the short－term demand for electricity:Do neural networks stand a better chance[J].International Journal of Forecasting,2000(1):71－83.

[4]Suykens,J A K.Nonlinear modelling and support vector machines[J].In:Proceedings of IEEE Instrumentation and Measurement Technology Confer－ence,2001(2－3):287－294.

[5]Vapnik,V.The nature of statistical learning theory[M].New York:Springer,1995:37－40.

[6]应剑烈,华国栋,刘耀年.基于v－SVR的短期电力负荷预测[J].东北电力大学学报,2007(2):43－48.

[7]Tipping M E.Sparse Bayesian learning and the relevance vector machine[J].Mach.Learn.Res.,2001(2):211－244.

[8]Tipping M E.Bayesian inference:An introduction to principles and practice in machine learning[J].Lectures Notes in Computer Science,2004(1):41－62.

[9]刘遵雄,张德运,孙钦东,徐 征.基于相关向量机的电力负荷中期预测[J].西安交通大学学报,2004(10):1005－1008.

[10]Zhang B R.,et al.A novel hybrid model for tourist volume forecasting incorporating search engine data[J].Asia Pacific Journal of Tourism Research,2017(3):245－254.

[11]Ghani J.,Choudhury I.,Hassan,H.Application of Taguchi method in the optimization of end milling parameters[J].Journal of Materials Processing Technology,2004(1):84－92.

[责任编辑 范 藻]

Forecasting Electricity Consumption Demand Based on Relevance Vector Machine: The Case Study of Beijing

ZHANG Binru,TANGYuping,HU Rong
(Mathematics School of Sichuan University of Arts and Sciences,Dazhou Sichuan 635000,China)

Scientific electricity consumption demand forecast plays an important role in the operation,management and decision－making of energy system.In view of the nonlinearity in the electricity consumption demand and some deficiencies of traditional forecast techniques,this study introduce relevance vector machine(RVM)and develop forecastmodel to predict consumption demand in Beijing.With the empirical analysis results suggesting that RVM can effectively improve the prediction accuracy compared to its counterparts including SVR and ANN models.Forecasted results can be referenced by the decision－making of relevant departments.

relevance vectormachine;electricity consumption demand;support vector regression;prediction accuracy

TM715

A

1674－5248(2017)05－0010－05

2017－04－17

四川省教育厅一般项目(17ZB0375);国家自然科学基金项目(71373023)

张斌儒(1980—),男,四川南江人.讲师,博士研究生,主要从事数量经济及旅游经济研究.