可压缩骨架土石坝渗流场与应力场耦合分析
王日升,赵明阶
(1.重庆交通大学 河海学院,重庆 400074 ;2.山东交通学院 交通土建学院, 山东 济南250347)
可压缩骨架土石坝渗流场与应力场耦合分析
王日升1, 2,赵明阶1
(1.重庆交通大学 河海学院,重庆 400074 ;2.山东交通学院 交通土建学院, 山东 济南250347)
在土石坝渗流过程中,土石复合介质孔隙中流体会产生压力变化,变化后的压力作用于土石复合介质的固相骨架颗粒上会引起孔隙率、骨架颗粒变形等一些列变化,变化后的孔隙及骨架颗粒又反过来作用于孔隙中的流体,引起其应力场的重分布,因此,在研究土石复合介质内流体的渗透规律时必须综合考虑孔隙流体的流动规律及其对孔隙应力的影响,考虑土石复合介质内应力场与渗流场的耦合作用,采用理论推导可压缩骨架土石坝耦合模型,并通过具体实例对比模型的准确性及合理性进行验证,验证表明考虑骨架压缩后的耦合结果的相对残差更小,更接近于实际的观测结果。
岩土工程;土石坝;渗流场;应力场;耦合
0 引 言
土石坝建设工程中所用的土石复合介质一般由土和岩石组成的固相、颗粒间孔隙中所含空气组成的气相及孔隙中所含充水组成的液相等几部分组成的多相介质体。由于土石介质体的固相是由土体中包含大小不同、形状各异、含量不一、分布不同的岩石块体所组成,因此其物理力学性质等既不同于传统意义上所说的土体,又不同于岩体,而是间于土体和岩体之间的一种特殊的介质,由其所形成的渗流场及其变形具有自身独特的特点。而经典渗流力学在求解渗流场的时候一般都假定流体是不可压缩的,并且流体流动的孔隙介质是刚性介质,流体在流动过程中所产生的任何压力变化对固体颗粒不会产生变形。张乾飞[1]在其学位论文中对复杂渗流场演变规律进行了研究,同时对神流场的转异特征进行了研究;李欣[2]在前人研究的基础上对渗流场进行了反演计算并将其反演规律应用在在水库渗漏控制中;S.P.PARKER[3]在其地质学与矿物学著作中对不同的地质状况的渗流场进行了详细的研究,他们研究的前提均基于空隙介质为刚性且系内流体无压缩性的经典渗流理论;梁越等[4]对多孔介质内的孔隙流动进行了数值建模,并对孔隙内存在的流速分布进行系统研究;满红飞[5]、栾艳[6]、田强[7]分别在其学位论文中对土石复合介质的渗流、渗漏机理及渗漏参数的影响因素等进行了详细的研究,然而他们虽对土石复合介质的渗流场进行了系统全面的研究,而在研究的同时并未对相应的应力场进行考虑,或虽有涉及但并不全面;耿计计[8]对土石坝的渗流场与应力场进行了耦合分析;周红星[9]对耦合后的双层堤基渗透破坏机理进行了数值模拟研究,他们虽然研究了土石复合介质的渗流场及应力场的耦合但并未考虑其介质的可压缩性。而实际上土石复合介质的固相尤其是土体为可变形体,受压缩过程中除了颗粒间孔隙会发生变化,颗粒本身也会产生变形。在实际的渗流过程中,由于介质孔隙中流体会产生压力变化,变化后的压力作用于土石坝土石复合介质的固相骨架颗粒上会引起孔隙率、骨架颗粒变形等一些列变化,变化后的孔隙及骨架颗粒又反过来作用于孔隙中的流体,引起其应力场的重分布,因此,在研究土石坝土石复合介质内流体的渗透规律时必须综合考虑孔隙流体的流动规律及其对孔隙应力的影响,考虑土石坝土石复合介质内应力场与渗流场的耦合作用。笔者基于流体力学的连续性方程、运动方程及介质三相体受压缩的状态方程建立起渗流场与应力场的耦合模型。
1 模型假设
单相液体渗流;假定所研究地层是水平、均质、各向同性的;液体是单相、均质、可压缩的牛顿液体,液体的流动过程中的切应力与应变的时间变化率,即速度梯度是成正比的;渗流过程中为温度不产生任何变化;渗流过程不存在任何特殊的物理化学现象;土石混合体是完全饱和各向同性体线弹性体;土石混合体的渗透系数与孔隙率是相关的,且孔隙率是动态变化的;渗流时符合Darcy线性渗流定律:
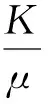
2 数学模型
2.1 连续性方程[10]
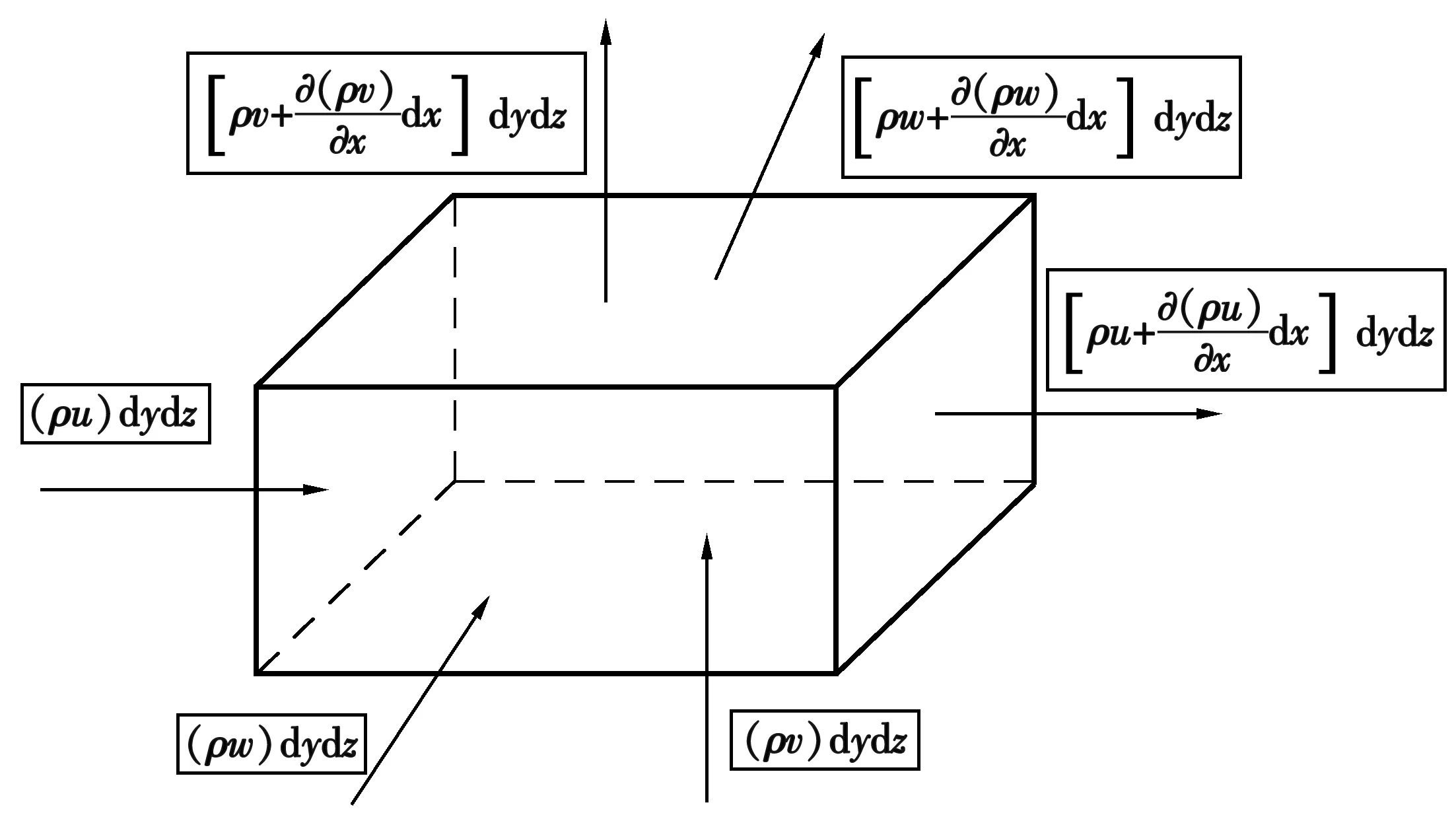
图1 连续性方程微团示意Fig.1 Micelle diagram of continuity equation
采用空间位置固定的无穷小微团模型。如图1以坐标正方向为正,X方向上净流出的流量为

同理Y方向上净流出的流量为

Z方向上净流出的流量为
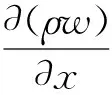
式中:ρu、ρv、ρw分别为质量速度在X、Y、Z方向上的分量。
由上述3式可知,微团控制体净流出量为
(1)
又考虑微团体的体积很小,因此其总质量为ρndxdydz,n为孔隙率,微团控制体内质量随时间变化率为
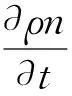
(2)

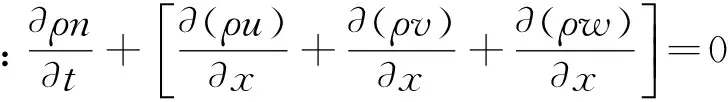
(3)
2.2 运动方程[11]
设渗流时符合Darcy线性渗流定律:
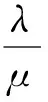
(4)

上述3式即为其运动方程。
式中:λ为渗透系数;μ为黏滞系数。
砂性土的渗透率可表示为[12]:
式中:e为孔隙比;n为孔隙率;D10为10%有效粒径;C2为由实验确定常数;Cn不均匀系数。
黏性土的渗透率可表示为[12]
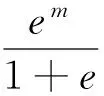
式中:e为孔隙比;n为孔隙率;C3、m均为为由实验确定常数。
2.3 状态方程[13]

(5)
式(5)即是微团体变化的状态方程,方程前两项分别是由骨架颗粒和孔隙压缩变形引起,后一项是由孔隙内水体压缩变形引起。三者的压缩变形引起的微团体孔隙变化从而导致孔隙内水体质量随时间产生变化。
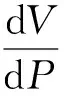
dV=KVdP
(6)
式(5)右边第2项表示空隙自身压缩变形,即:
d(1-n)V=0
(7)
微分后可得:

(8)
对式(8)分离变量并积分:
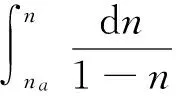

即: 1-n=-(1-na)eK(P-Pa)
所以:n=1+(1-na)eK(P-Pa)
将eK(P-Pa)展开并略去二次以上高阶项知:
eK(P-Pa)=1+K(P-Pa)
即:n=1+(1-na)[1+K(P-Pa)]
(9)
式中:na、n为压缩前后的孔隙率;K为骨架颗粒的压缩性。
式(5)中右边第3项表示微元体内孔隙水的压缩变形。水的压缩性:
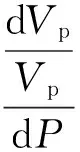
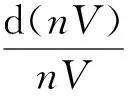
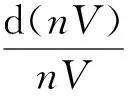
故可知:dρ=ρβdP
(10)
对上式分离变量并积分可得:

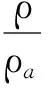
故:ρ=ρaeβ(P-Pa)
将eβ(P-Pa)展开并略去二次以上高阶项知:
eβ(P-Pa)=1+β(P-Pa)
即:ρ=ρa[1+β(P-Pa)]
(11)
式中:ρ为压缩后孔隙水密度;ρa为压缩前孔隙水密度;β为孔隙水的压缩系数;Pa、P为压缩前后压强。
2.4 骨架、孔隙水可压缩土石坝基本微分方程
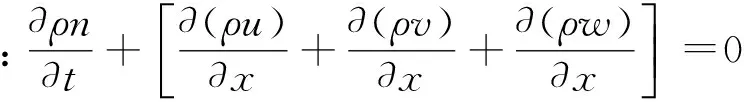
运动方程:

状态方程:ρ=ρa[1+β(P-Pa)]
联立求解:
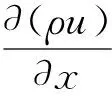

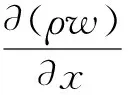
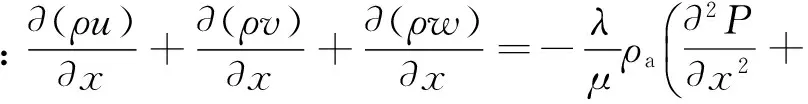
(12)
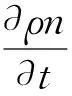
其中:
{ρa[1+β(P-Pa)]}{1+(1-na)[1+K(P-Pa)]}=[ρa+ρaβ(P-Pa)][1+(1-na)+(1-na)K(P-Pa)]=(2-na)ρa+ρa(1-na)K(P-Pa)+(2-na)ρaβ(P-Pa)+(1-na)ρaβK(P-Pa)2
由于骨架颗粒压缩性K及水的压缩性β均很小,故二者的乘积可忽略不计,即上式可近似:
(2-na)ρa+ρa(1-na)K(P-Pa)+(2-na)ρaβ(P-Pa)=ρa(P-Pa)(K+2β)-ρana(β+K)(P-Pa)=ρa(K+2β)P-ρa(K+2β)Pa-ρana(β+K)P+ρana(β+K)Pa
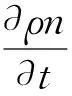

(13)
所以联立式(12)、式(13)可得:

(14)
式(14)即为骨架颗粒及孔隙水可压缩的土石坝渗流场与应力场的耦合方程。
考虑边界条件后的耦合数学模型:
(x、y、z∈Ω)
(15)
H(x、y、z)=H1(x、y、z)(x、y、z∈Γ1)
(16)
(17)
(18)
式中:Ω为渗流区域;H(x、y、z)为渗流区水头分布函数;Γ1为第1类边界条件;H1(x、y、z)为其上的水头;Γ2为第2类边界条件;n2为Γ2的法线方向;q(x、y、z)为Γ2上的流量分布;Γ3为渗流自由面边界;n3为Γ3的法线方向。
3 模型验证
笔者在模型验证中取文献[14]中花凉亭水库土坝渗流观测资料,最高上游水位与最低上游水位来进行计算,相应最高上游水位时的资料:上游水位为54.61 m,下游水位为14.98 m,坝体材料渗透系数见表1[14]:

表1 坝体材料渗透系数
通过对水库土坝进行分点观测、采用不计压缩耦合方程计算值、计入压缩耦合方程计算值进行计算,其计算结果见表2。
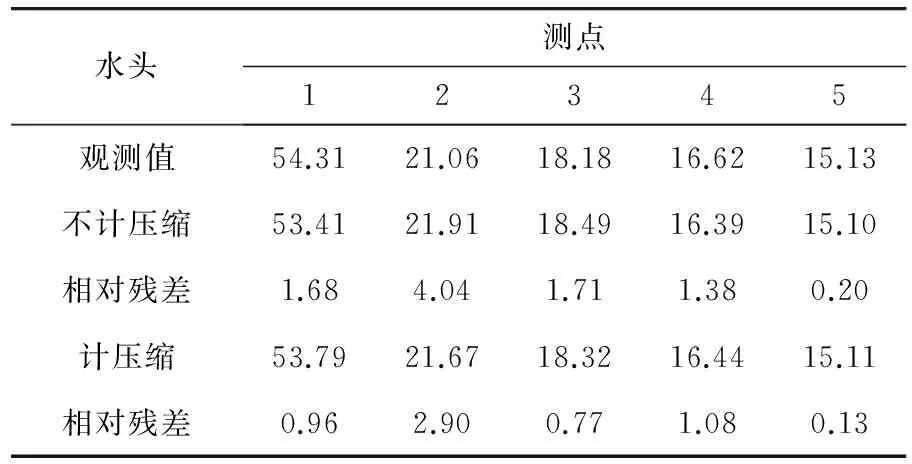
表2 观测值及计算值
将不计压缩和计入压缩耦合方程计算值与现场实验的观测值进行数值拟合,其拟合度见图2。
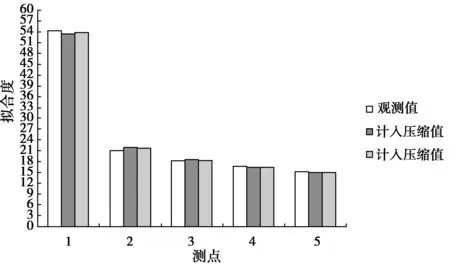
图2 各测点拟合度Fig. 2 Fitting of each measuring point
由表2分析可知,计入骨架颗粒及孔隙水可压缩的土石坝渗流场与应力场的耦合方程的水头计算值各点的平均残差为4.7%,优于未计入骨架颗粒及孔隙水可压缩的平均残差7.2%,因此其更接近于实际值。由图2可以看出,计入骨架颗粒及孔隙水可压缩的土石坝渗流场与应力场的耦合方程的各点水头计算值与观测值的拟合度更好。
相对残差较之于未计入骨架颗粒及孔隙水可压缩的虽然减少了2.5%,但仍然存在,其原因主要产生于以下两方面:一是在所建立的模型时并未实际考虑渗流过程中温度变化的影响;二是将土石坝坝体材料视为了完全饱和的各向同性体线弹性体,而实际中其并不是完全各项同性的,并且也不是完全饱和的弹性体,因此以上两方面引起了误差。
4 结 论
1)通过流体力学的连续性方程、运动方程及介质三相体受压缩的状态方程建立起渗流场与应力场的耦合模型,并给出了数学表达式。
2)由于现行的渗流场求解过程一般不考虑骨架颗粒的可压缩性,故考虑渗流场与应力场耦合后的方程更具有工程实际应用意义。
3)所建物理模型中未考虑渗流过程中为温度产生变化,实际应用过程中温度会是一个变化的影响因素。
4)物理模型中为简化期间将土石混合体视为完全饱和各向同性体线弹性体,实际应用中应根据复合土石坝土体的情况单独考虑。
5)土石坝坝体材料特殊,其内部渗流场及应力场既不同于纯岩体材料也不同于纯土体材料,更不是简单的将二者折中叠加,其内部存在自身独特的耦合规律,因此将土石坝坝体材料骨架的压缩性计入并将渗流场与应力场进行耦合分析,对于土石坝渗流场与应力场的研究更具实际意义。
[1] 张乾飞.复杂渗流场演变规律及转异特征研究[D].南京:河海大学,2002:46-50. ZHANG Qianfei.SeepageofEvolutionandTransferCharacteristics[D].Nanjing:Hohai University,2002: 46-50.
[2] 李欣. 渗流场反演计算及在水库渗漏控制中的应用研究[D]. 长春:吉林大学, 2004. LI Xin.SeepageFieldInversionCalculationandApplicationoftheSeepageControl[D]. Changchun: Jilin University, 2004.
[3] PARKER S P.DictionaryofGeologyandMineralogy[M].New York: McGraw-Hill, 2003: 199-204.
[4] 梁越,陈建生,陈亮.孔隙流动数值模拟建模方法及孔隙流速分布规律[J].岩土工程学报,2011,33(7):1104-1109. LIANG Yue, CHEN Jiansheng, CHEN Liang. Pore flow numerical simulation modeling and pore velocity distribution[J].GeotechnicalEngineeringEducation, 2011, 33(7):1104-1109.
[5] 满红飞.土石坝渗流安全性态分析研究及工程应用[D].南京:南京水利科学研究院,2009:33-39. MAN Hongfei.SeepageEmbankmentDamSafetyBehaviorAnalysisandEngineeringApplications[D].Nanjing:Hydraulic Research Institute, 2009: 33-39.
[6] 栾艳.土石坝渗透规律与渗漏机理研究[D].重庆:重庆交通大学,2009:46-49. LUAN Yan.EmbankmentDamInfiltrationLawandLeakageMechanism[D].Chongqing: Chongqing Jiaotong University, 2009: 46-49.
[7] 田强.土石坝动力参数的反演算法研究[D].大连:大连理工大学,2012:51-57. TIAN Qiang.InversionStudyonDynamicParametersofEmbankmentDams[D].Dalian:Dalian University of Technology, 2012: 51-57.
[8] 耿计计.基于渗流场与应力场祸合分析的土石坝绕坝渗流问题研究[D].西安:西安理工大学,2010:63-69. GENG Jiji.ResearchAroundtheDamEmbankmentDamSeepageProblemBasedonSeepageFieldandStressFieldCouplingAnalysis[D].Xi’an:Xi’an University of Technology, 2010: 63-69.
[9] 周红星.双层堤基渗透破坏机理和数值模拟研究[D].长沙:华南理工大学,2011:66-70. ZHOU Hongxing.DoublePenetrationFailureMechanismEmbankmentFoundationandNumericalSimulation[D].Changsha:South China University of Technology, 2011: 66-70.
[10] 王俊杰,陈亮,梁越.地下水渗流力学[M]. 北京:中国水利水电出版社,2013:64-71. WANG Junjie, CHEN Liang, LIANG Yue.GroundwaterSeepageStylistics[M].Beijing:China Water Power Press, 2013: 64-71.
[11] 张伟,陈文义.流体力学[M].2版.天津:天津大学出版社, 2009. ZHANG Wei, CHEN Wenyi.Hydromechanics[M].2nded.Tianjin:Tianjin University Press, 2009.
[12] 柴军瑞,徐维生. 大坝工程渗流非线性问题[M]. 北京:中国水利水电出版社, 2010. CHAI Junrui, XU Weisheng.DamNonlinearProblemofSeepageinDamEngineering[M].Beijing: China Water Power Press, 2010.
[13] 陈洪凯.高等土力学[M].北京:中国科学文化出版社,2000:47-64. CHEN Hongkai.AdvancedSoilMechanics[M].Beijing: China Science and Culture Publishing House, 2000: 47-64.
[14] 张媛媛.ANSYS在土坝渗流场和应力场及其耦合分析中的应用研究[D].南京:河海大学,2006:63-69. ZHANG Yuanyuan.TheApplicationandStudyofANSYSonSeepageField,StressFieldandCouplingAnalysisforEarthDam[D].Nanjing:Hohai University, 2006: 63-69.
(责任编辑:朱汉容)
CouplingAnalysisofSeepageFieldandStressFieldofCompressibleSkeletonEarth-RockDams
WANG Risheng1, 2, ZHAO Mingjie1
(1. School of River & Ocean Engineering, Chongqing Jiaotong University, Chongqing 400074, P.R.China;2. School of Traffic and Civil Engineering, Shandong Jiaotong University, Jinan 250347, Shandong, P.R.China)
In the process of seepage flow of earth-rock dams, the liquid in the pore of soil-stone composite medium would produce pressure change, which acted on the solid skeleton particles of soil-stone composite medium and resulted in a series of changes, such as porosity and deformation of skeleton particle. The porosity and skeleton particle after changes worked on the liquid in the pores in turn and caused the redistribution of its stress field. Hence, the flow regularity of the liquid in the pores and its influence on porosity stress and the coupling effect of stress field and seepage filed must be taken into account in the research of permeability rule for the liquid in soil-stone composite medium. The coupling model of compressible skeleton earth-rock dam was deduced on the basis of related theories. The accuracy and rationality of the proposed model are verified through comparing specific examples, and the verification shows that the relative residuals of coupling results are smaller and closer to actual observation results when the compression of skeleton is taken into account.
geotechnical engineering; earth-rock dam; seepage field; stress field; coupling
TV314
:A
:1674- 0696(2017)09- 061- 05
10.3969/j.issn.1674-0696.2017.09.12
2015-12-28;
:2016-01-20
国家自然科学基金资助项目(51279219)
王日升(1979—),男,山东招远人,博士,主要从事土石坝渗漏检测研究。E-mail:42149817@qq.com。

