基于孔隙演化的砂土冲击绝热关系研究
高 飞, 邱艳宇, 王明洋, 张先锋, 程怡豪
(1. 南京理工大学 智能弹药国防重点学科实验室, 南京 210094; 2. 解放军理工大学 爆炸冲击防灾减灾国家重点实验室, 南京 210007)
基于孔隙演化的砂土冲击绝热关系研究
高 飞1,2, 邱艳宇1,2, 王明洋1,2, 张先锋1, 程怡豪2
(1. 南京理工大学 智能弹药国防重点学科实验室, 南京 210094; 2. 解放军理工大学 爆炸冲击防灾减灾国家重点实验室, 南京 210007)
基于砂土多孔、含水的特性,对动载荷作用下孔隙演化对砂土冲击绝热关系的影响进行了研究。基于砂土基体的不可压缩假设,采用单个球形气孔等效模型和广义Mises屈服准则推导了砂土考虑孔隙压实的演化方程;根据冲击Hugoniot突跃条件和Grüneisen型方程,获得了砂土考虑孔隙演化的状态方程;根据混合物冲击波关系和孔隙演化状态方程,获得了砂土基体材料冲击绝热关系、干砂土和湿砂土冲击绝热关系,并与已有实验结果进行了对比。结果表明:计算得到的绝热线与实验数据吻合较好,该孔隙演化状态方程能够较为准确的反映动载作用下砂土的动态响应过程。
砂土; 孔隙演化; Grüneisen型状态方程; 冲击绝热关系
砂土是自然界普遍存在的地质材料,是由砂土颗粒、水和空气构成的多组分、多相、非均匀混合物。砂土及其它多孔颗粒介质动态力学行为的研究对许多工程应用,如地震工程、侵彻研究、陶瓷装甲性能研究等都有重要的参考价值[1]。目前,国内对于砂土的研究主要集中在强度理论、剪胀理论及本构模型方面[2-6],其动态力学行为的研究较少涉及。砂土动态响应过程很大程度上受颗粒尺寸、孔隙率及含水量的影响,尤其是含水量及孔隙率的不同,对砂土中冲击波的传播规律有着显著的影响。
研究表明[7],含水量(湿度为3%~20%)对砂土的动态应力应变关系影响很大,湿砂比干砂具有更好的可压缩性,且湿度为7%的湿砂表现的最软(可压缩性最好),并不是含水量越高的湿砂可压缩性越好。Proud等[8]研究在不同应变率范围内含水量对砂力学响应的影响规律,结果表明含水量在不同应变率区间的作用机理十分复杂,在低应变率时水起到润滑作用,而在高应变率时水的介入可能会出现砂越来越难压的现象。Brown等[1]通过飞片冲击实验,得到了砂的Hugoniot关系,修正了经典P-α模型。Borg等[9]研究冲击压缩条件下压实模型对于描述不同初始孔隙率砂的动力学响应时,发现P-α型压实模型与Grüneisen型状态方程的组合所得到的压力时程曲线能够更好地再现实验结果。
本文将微观不均匀多孔介质等效为均匀介质处理,将砂土内部分散的孔隙等效为仅包含单个气孔的球形颗粒介质,基于广义Mises准则推导了另一种形式的孔隙压实P-α方程,建立了考虑孔隙压实效应的多孔材料状态方程,计算了砂土基体材料和多孔材料的冲击绝热关系,与已有的Hugoniot实验数据对比,证明了孔隙演化方程和状态方程的合理性。该简化模型与研究思路对深入研究砂土及其它多孔介质动态力学行为具有参考意义。
1 基本模型与孔隙演化方程
1.1基本假设与等效模型
对砂土这种非均匀多孔介质,把它看作是水和石英组成的双组分混合物,基体是水和石英,夹杂物是气孔。孔隙率变化对砂土力学性能的影响不容忽视,为此有必要建立考虑孔隙动态演化的方程。在推导这个方程时建立了如下模型,认为含大量初始孔隙的砂土与内部仅包含单个气孔的球形颗粒的表现是相似的[10],如图1所示,气孔周围是砂土基体材料,模型内、外半径分别为a,b,相应内、外半径初始值分别为a0、b0,且孔隙体积、基体体积均与原物质相同,这就保证了初始孔隙率的不变。距离平面中心b处作用有径向压力pm。在推导孔隙动态演化方程过程中假设如下:
(1) 基体材料是均匀和各向同性的、不可压且满足广义Mises屈服准则;
(2) 基体中气孔的分布在各向均匀;
(3) 忽略气孔的表面能和气孔中气体的压力,假定基体材料与多孔材料的内能是恒等的(亦即多孔材料的内能是由基体的应变决定的);
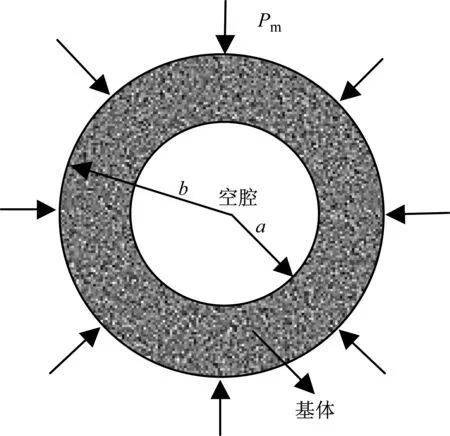
图1 砂土的孔隙演化等效模型
(4) 在分析气孔周围材料处于塑性状态时,忽略了气孔的弹性阶段微小压缩量。
1.2孔隙演化动力学方程
对多孔材料用参数α表示其密实程度:
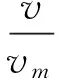
(1)
式中:v为多孔介质的总体积;vm为基体的体积;ρ为多孔介质的密度;ρm为基体的密度;当α=1时材料达到完全密实状态。
如果忽略气孔的表面能和气孔中气体的压力,则多孔材料的状态方程与基体材料具有相同的形式,而多孔材料中的压力P与基体材料中的压力Pm有如下关系式[11]:
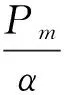
(2)
引入中心在平面上的球坐标系(r,θ,φ),其即时半径用a表示。设距离平面中心b处作用有应力:
σr=-Pm=-αP
(3)
式中:
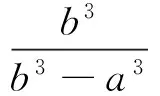
(4)
假定基体材料是不可压缩的,则球形坐标下的控制方程组可表示为
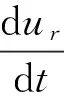
(5)
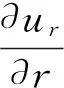
(6)
σr-σθ=Y0+kPm=Y0-k(σr+2σθ)/3
(7)
式中,ur为径向速度;σr、σθ分别为径向应力和环向应力;Y0、k分别为黏结力和摩擦因数。
含气孔的球形颗粒内外边界的边界条件是:
σr(b,t)=-αP,σr(a,t)=0
(8)
对式(6)积分,可得:
(9)
式中:
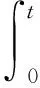
(10)
利用边界点(a,a0)、(b,b0),可得:
(11)
由式(4),可知:
(12)
即可确定函数:
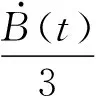
(13)
并得到加速度:
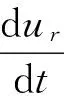
(14)
这样,考虑到式(7),方程(5)可表示为
(15)
求解该方程,可得解:
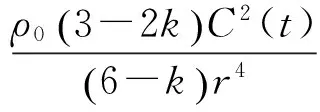
(16)
分别利用式(8)的两个边界条件并考虑到下式:
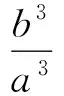
(17)
最终可得:
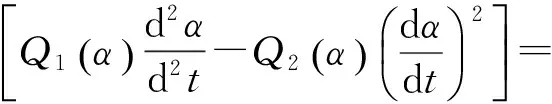
(18)
式中:
(19a)
(19b)
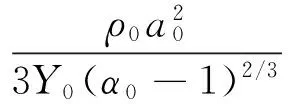
(19c)
式(18)在下列条件时(气孔周围材料已进入塑性状态,此时孔隙的变化可观察到)可用于确定α:
(20)
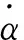
(21)
图2是根据方程式(21)得到的压力-孔隙率变化时砂土的加载-卸载曲线图,是另一种形式的P-α模型。在1-2初始加载阶段,砂土压缩时孔隙率α0没有变化,因为气孔收缩的弹性和弹塑性分量很小,忽略不计。当压力按照方程式(21)的变化规律继续增大时(2-3段),砂土颗粒材料产生了不可逆地压实 (α逐渐减小逼近1)。卸载阶段,材料在孔隙率恒定的条件下,由点3卸载至点4 (P=0)。
对于孔隙介质冲击压缩曲线,也可以用Herrmann[12]提出的P-α模型描述压力与孔隙率的关系,分弹性和塑性阶段,如图3所示。当压力小于弹性极限压力Pe时,材料处于弹性阶段,且孔隙率的变化是可逆的,压力与孔隙率有如下关系[13]:
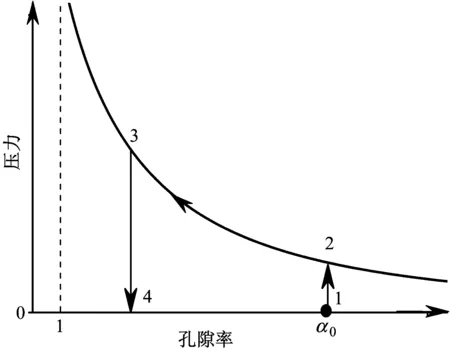
图2 砂土压力与孔隙率的加卸载演化曲线
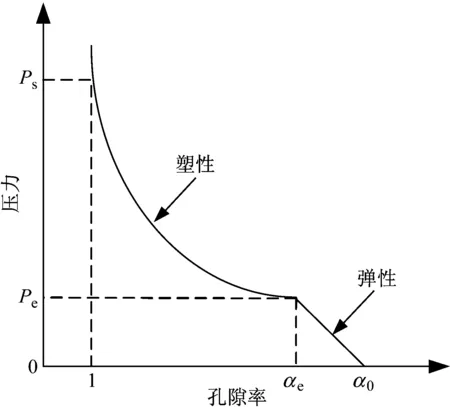
图3 典型的孔隙介质压力与孔隙率变化曲线[12]
(22a)
(22b)
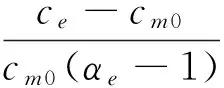
(22c)
αe=α(P=Pe)
(22d)
利用式(22)可以计算由初始孔隙率α0到弹性极限孔隙率αe的微小变化,由于孔隙率变化很小,一般假设在弹性阶段满足:dα/dP=0,即认为ce=cm0。
在P>Pe的塑性阶段,通常用多项式的形式表示压力与孔隙率的关系[14]:
(23)
式中:Pe和Ps均为材料常数,分别表示砂土刚进入塑性阶段和压密时对应的压力值。
在忽略弹性阶段孔隙率的微小变化后,式(21)表示的P-α关系曲线与Herrmann提出的经典P-α模型在砂土变形的塑性阶段相似,仅仅是函数形式和模型参数不同。
2 砂土的状态方程与冲击绝热关系
本节首先建立孔隙演化砂土Grüneisen型状态方程;然后利用混合物冲击波关系,求砂土基体的冲击Hugoniot线;最后根据砂土状态方程求干砂和湿砂的冲击Hugoniot线,并与实验数据对比。
2.1基于孔隙演化的砂土状态方程
因为砂土中夹杂空气的质量与砂土颗粒相比小几个数量级,故气孔内空气的影响可以忽略不计,因此干砂就可以看作以石英为基体的多孔材料,夹杂物是气孔;湿砂则看作以石英和水为基体的简单二组分混合物,夹杂物是气孔。利用基体的Hugoniot参数和Grüneisen型状态方程,便可得到砂土的状态方程。若利用基体材料冲击波速Dm与质点速度Um的简单线性关系:
Dm=cm0+qm0Um
(24)
根据冲击波波阵面的突跃条件和Grüneisen型方程,基体材料的状态方程可表示为
Pm=PH+γmρm(Em-EH)
(25)
(26)
式中:PH为冲击绝热线上的压力;γm为与ρm对应的Grüneisen系数;ρm0为基体初始密度;EH为冲击波波阵面上基体的比内能;Em为与ρm、PH对应的基体比内能。
根据冲击波波阵面上的守恒条件:
(27)
对砂土而言,假设条件与2.1节相同,忽略气孔的表面能和气孔中气体的压力,假定基体材料与多孔材料的内能相等(即Em=E(ρ,P),E为砂土的比内能),将式(27)、式(26)、式(1)、式(2)代入式(25),并利用Grüneisen假定关系:γmρm=γm0ρm0,则压缩时砂土多孔材料的状态方程为
(28)
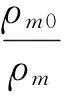
(29)
2.2砂土基体材料冲击绝热关系
根据混合物冲击波关系式:
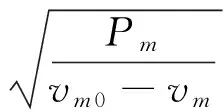
(30)
将式(30)代入式(24),可得:
(31)
对于砂土混合物的基体(即暂不考虑孔隙)而言,以(νm,Pm)为变量的冲击绝热关系可表示为
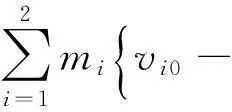
(32)
式中:m1=ω0/(1+ω0),m2=1/(1+ω0)分别为砂土中水和石英的质量分数(m1+m2= 1),ω0为砂土的质量湿度;νi0、ρi0(i=1, 2)分别为水、石英的初始比容和密度。计算用到的水、石英及其混合物线性关系Hugoniot参数见表1。

表1 水、石英和两者混合物的线性关系Hugoniot参数[17]
图4是以(νm,Pm)和(Um,Dm)为变量的砂土基体材料冲击绝热曲线,水的绝热曲线是1,石英的绝热曲线是2,密度ρ0=1.8 g/cm3,湿度为28%砂土基体混合物(水和石英)的绝热曲线是3。由图4 (a)的结果得出,在100 GPa压力范围内以混合物冲击波关系和线性关系表示的Pm-νm线,水由初始比容1 cm3/g压缩到了0.45 cm3/g,压缩量为55%;石英由初始比容0.376 cm3/g压缩到了0.25 cm3/g,压缩量为33.5%;水和石英的基体混合物由初始比容0.513 cm3/g压缩到了0.3 cm3/g,压缩量为41.5%。基体混合物的Hugoniot线界于水和石英的之间,这也是符合混合物理论基本规律的。
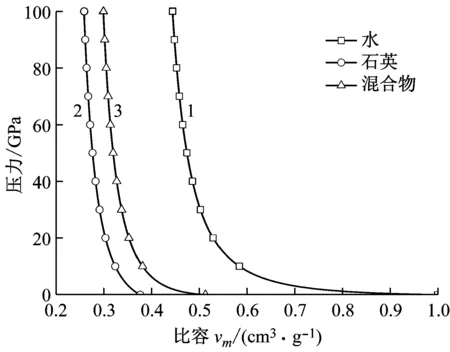
(a) 比容与压力的关系
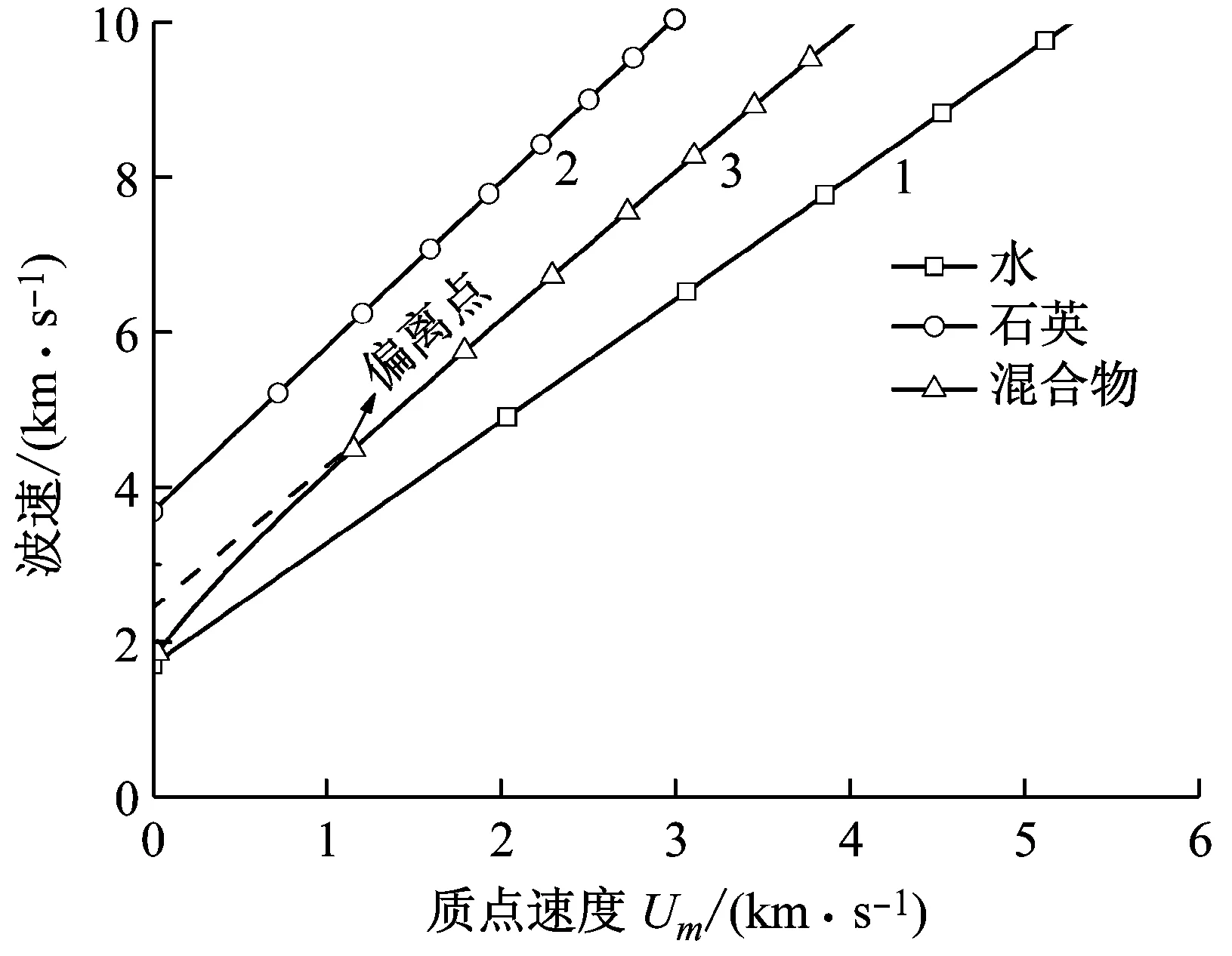
(b) 质点速度与波速的关系
由图4 (b)可以看出,由式(30)表示基体冲击波速度与质点速度关系时,就某单个组分而言,水或石英的Dm-Um线的线性关系十分好,且在质点速度为0 km/s时对应的冲击波速度(即体积声速c0)也与表1的值吻合很好。水和石英混合物的Dm-Um线可以分为两段:在低压段(当物体具有弹性力学行为时),Dm-Um线在Um=1.15 km/s 时向下偏折,主要原因是,在建立固体高压状态方程时一般不计剪切强度的影响,这种假设在高压阶段较为合理,但低压段剪切强度已逐渐恢复,若仍不考虑剪切强度将会低估压力值(或波速)的大小,发生曲线向下偏折的现象,通常理论计算得到的波速-质点速度关系都是如此[15];在高压段(当物体具有流体力学行为时),即Um>1.15 km/s 时,Dm-Um线的线性规律还是比较好的。在不考虑局部线性偏离的情况下,在相当宽广的压力范围内,Dm-Um线基本能够表征砂土基体材料的冲击压缩特性。
目前对于固体在高压作用下的动力性质研究较多,而对于低应力区与高应力区之间的过渡区的研究工作相对较少,这一过渡区的范围对于强度大的物体来讲(金属、岩石及混凝土)大约从数百兆帕到数十吉帕,在这一压力范围内实现了从弹性状态到内摩擦状态,甚至到流体动力学状态的转换,十分复杂[16]。由公式P=ρDmUm,计算得到偏折点处对应的压力值约10 GPa,该点恰好处于这一应力过渡区,这种应力状态的转换也解释了发生偏折现象的物理本质。
为分析初始孔隙率和湿度对砂土Hugoniot线的影响,根据方程(21)和表2参数计算了干砂土(α0=2.062)和湿砂土(α0=1.083,ω0=28%)的P-α曲线,如图5。图5(a)为干砂土的P-α曲线,发现干砂土达到密实态(α=1)所需的压力值为20 GPa;而图5(b)湿砂土达到密实态的压力值为5 GPa,可能是因为水起到了润滑作用,砂粒间摩擦力减小,使原来松散多孔介质更容易向密实态转变。可见,同样是砂土,当初始孔隙率和湿度不同时,材料冲击压缩响应会有较大差异,进一步明晰了孔隙率和湿度在研究砂土类多孔介质时的重要性。
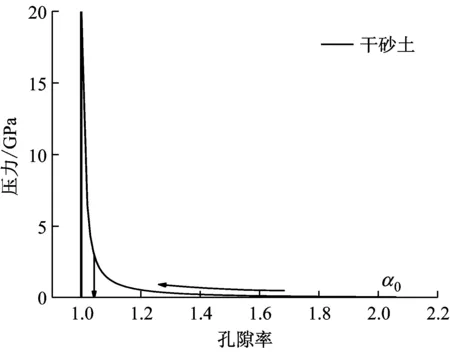
(a) 干砂土孔隙演化曲线
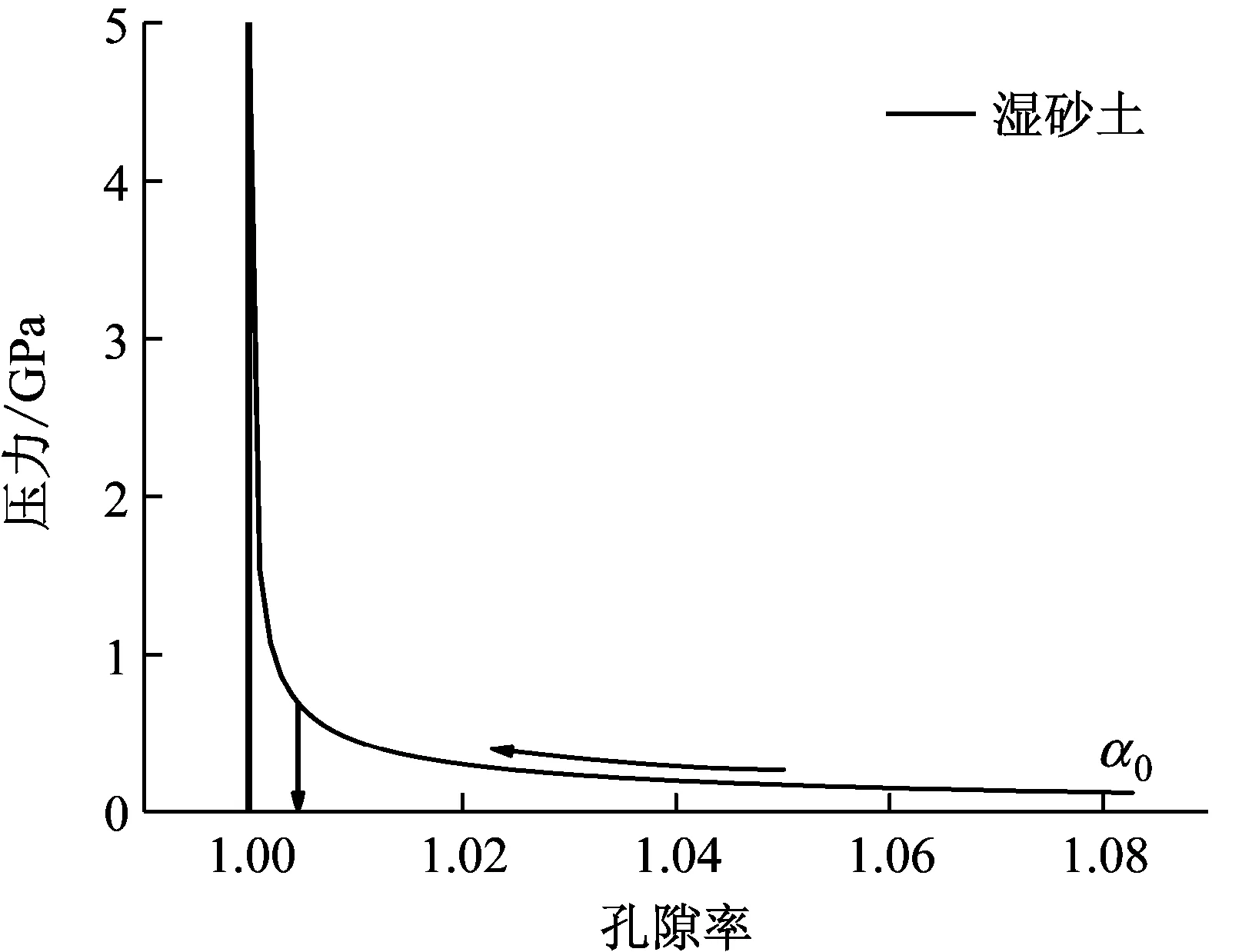
(b) 湿砂土孔隙演化曲线

材料ρ0/(g·cm-3)ω0/%ν空气/%ρm0/(g·cm-3)cm0/(m·s-1)qm0γm0Y0/GPak干砂土1.29051.52.6636802.121.00.10.75湿砂土1.80287.751.9524501.861.280.0250.5
2.3砂土材料冲击绝热关系
根据2.1节的砂土多孔材料状态方程和表2参数计算了以(ν,P)和(U,D)为变量的干砂土和湿砂土的Hugoniot线,如图6所示,实线和虚线代表计算值,实心黑点和空心圆圈代表实验值[17]。
图6 (a)给出了12 GPa压力范围内计算得到的干砂土和湿砂土P-νHugoniot线,与实验结果吻合较好,在高压段的计算值与实验值的偏差比低压段稍大。干砂土由初始比容0.775 cm3/g压缩到了0.334 cm3/g,压缩量为57%;湿砂土由初始比容0.555 cm3/g压缩到了0.382 cm3/g,压缩量为31.2%。值得注意的是,干砂土和湿砂土的P-ν线在ν=0.5 cm3/g时交叉,在ν=0.5-0.775 cm3/g 时干砂土的P-νHugoniot线几乎为水平线,主要是因为干砂土的初始孔隙率(α0=2.062)大,而压缩气孔所需的压力值很小,故此阶段压力变化不明显,当ν=0.5 cm3/g (对应α=1.33)时,气孔几乎完全崩塌而逐渐开始压缩固体颗粒,故压力值陡增;对于湿度为28%的湿砂土,由于水的存在填充了大部分孔隙,使得材料在初始阶段(α0=1.083)就已经接近密实态,故在一开始比容的微弱变化就使压力明显增大。对比图6 (a)干砂土和湿砂土P-νHugoniot线上联结终态点与初态点的弦线(即Rayleigh线)斜率,发现湿砂Rayleigh线的斜率绝对值明显大于干砂Rayleigh线的斜率绝对值,表明相同冲击条件下湿砂中冲击波物质波速大于干砂中冲击波物质波速,主要原因是在干砂土中,存在相当数量的气孔,气孔的存在使得冲击波的能量很大程度上耗散在气孔变形与压溃,进而影响了冲击波的传播。而水的介入,一方面增加了湿度,另一方面也减小了孔隙率,起到填充孔隙均衡材料的作用,使得冲击波速度有着显著的提高。
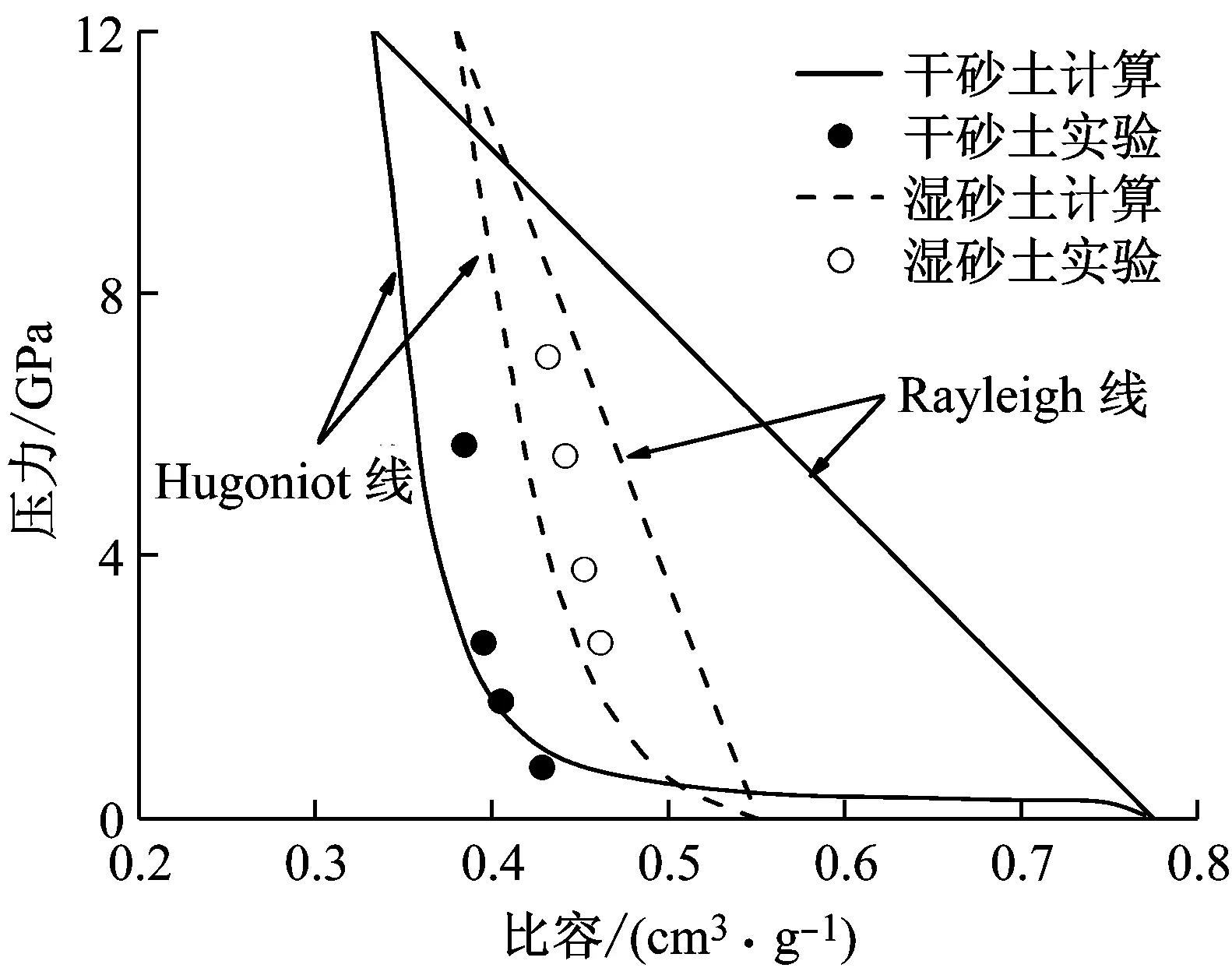
(a) 比容与压力曲线
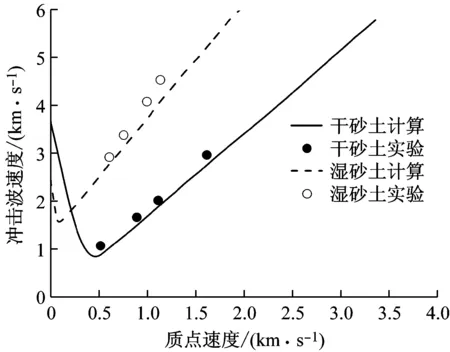
(b) 质点速度与波速曲线
Fig.6 Comparison of computation and experiment (adapted from Belov et al.[17]) shock adiabatic curves for dry sand and moist sand
图6 (b)给出了计算得到的干砂土和湿砂土的D-U线,计算值与实验结果吻合较好,需要注意的是,在低压区干砂土和湿砂土的D-U线发生了向上偏折的现象,但整体而言还是符合基本规律的。Herrmann[12]和Белов[18]在利用Grüneisen型状态方程计算多孔金属铁及Al2O3多孔陶瓷的D-U线时,低压段都发生了向上偏折的现象,但均未给出合理的解释。状态方程式(28)在描述物质热力学特性时准确性是有限的,这主要受限于参数γ取常数,实际上Grüneisen系数取决于密度和温度。此外,这个状态方程可以成功的描述在高密度和高温度下物质的热力属性,不能很好的描述密度很低时的压力特性,这也是低压区发生偏折的原因。总体而言,本文基于孔隙演化推导的砂土状态方程在描述其冲击Hugoniot线时是可行的,无论是P-ν线还是D-U线,计算值与实验值吻合都较好。
3 结 论
基于单个球形气孔颗粒模型和广义Mises屈服准则,推导了孔隙压缩演化方程,建立了砂土考虑孔隙演化的状态方程,计算了砂土基体、干砂土、湿砂土的Hugoniot关系,与实验结果吻合较好。主要结论如下:
(1) 基于相关假设推导的孔隙演化动力学方程在忽略气孔弹性阶段的微小变化后,与经典P-α模型在变形的塑性阶段相似,仅仅是函数形式和模型参数不同。
(2) 由孔隙演化动力学方程的计算结果可知,干砂土和湿砂土达到密实态所需的压力值差别很大,在研究砂土类多孔介质冲击压缩特性时要重点关注孔隙率和湿度这两个特征量。
(3) 根据孔隙演化状态方程计算的干砂土和湿砂土Hugoniot线与实验结果吻合较好,证明了简化模型与假设的合理性,表明状态方程可用于砂土的冲击压缩计算;由于数据的不足,该模型是否适用于其他多孔介质的计算还需要进一步实验验证。
(4) 建立的状态方程在计算D-U线时,在低压过渡段发生了向上偏折现象,并给出了初步的解释;低应力区与高应力区之间的过渡区的研究工作相对较少,有必要在未来的研究中加以重视。
[1] BROWN J L, VOGLER T J, GRADY D E, et al. Dynamic compaction of sand[C]// American Institute of Physics Conference Proceedings. American Institute of Physics, 2007, 1363-1366.
[2] 周健, 池永. 砂土力学性质的细观模拟[J]. 岩土力学, 2003, 24(6): 901-906.
ZHOU Jian, CHI Yong. Mesomechanical simulation of sand mechanical properties[J]. Rock and Soil Mechanics, 2003, 24(6): 901-906.
[3] 蔡正银, 李相菘. 砂土的剪胀理论及其本构模型的发展[J]. 岩土工程学报, 2007, 29(8): 1122-1128.
CAI Zhengyin, LI Xiangsong. Development of dilatancy theory and constitutive model of sand[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(8): 1122-1128.
[4] 常在, 杨军, 程晓辉. 砂土强度和剪胀性的颗粒力学分析[J]. 工程力学, 2010, 27(4): 95-104.
CHANG Zai, YANG Jun, CHENG Xiaohui. Granular mechanical analysis of the strength and dilatancy of sands[J]. Engineering Mechanics, 2010, 27(4): 95-104.
[5] 李学丰, 黄茂松, 钱建固. 宏细观结合的砂土各向异性破坏准则[J]. 岩石力学与工程学报, 2010, 29(9): 1885-1892.
LI Xuefeng, HUANG Maosong, QIAN Jiangu. Failure criterion of anisotropic sand with method of macro-meso incorporation[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(9): 1885-1892.
[6] 张建民. 砂土动力学若干基本理论探究[J]. 岩土工程学报, 2012, 34(1): 1-50.
ZHANG Jianmin. New advances in basic theories of sand dynamics[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(1): 1-50.
[7] MARTIN B E, CHEN Weinong, SONG Bo, et al. Moisture effects on the high strain-rate behavior of sand[J]. Mechanics of Materials, 2009, 41: 786-798.
[8] PROUD W G, CHAPMAN D J, WILLIAMSON D M, et al. The dynamic compaction of sand and related porous systems[C]// American Institute of Physics Conference Proceedings. American Institute of Physics, 2007, 1403-1408.
[9] BORG J P, COGAR J R, LLOYD A, et al. Computational simulations of the dynamic compaction of porous media[J]. International Journal of Impact Engineering, 2006, 33: 109-118.
[10] CARROLL M M, HOLT A C. Static and dynamic porecollapse relations for ductile porous materials[J]. Journal of Applied Physics, 1972, 43(4): 1626-1636.
[11] CARROLL M M, HOLT A C. Suggested modification of the Pα model for porous materials[J]. Journal of Applied Physics, 1972, 43(2): 759-761.
[12] HERRMANN W. Constitutive equation for the dynamic compaction of ductile porous materials[J]. Journal of Applied Physics, 1969, 40(6): 2490-2499.
[13] JUTZI M, BENZ W, MICHEL P. Numerical simulations of impacts involving porous bodies: I. Implementing sub-resolution porosity in a 3D SPH Hydrocode[J]. ICARUS, 2008, 198: 242-255.
[14] BORG J P, MORRISSEY M P, PERICH C A, et al. In situ velocity and stress characterization of a projectile penetrating a sand target: experimental measurements and continuum simulations[J]. International Journal of Impact Engineering, 2013, 51: 23-35.
[15] 经福谦. 实验物态方程导引[M]. 北京: 科学出版社, 1986.
[16] 戚承志, 钱七虎. 岩体动力变形与破坏的基本问题[M]. 北京: 科学出版社, 2009.
[17] BELOV N N, KOPANITSA D G, KUMPYAK O G, et al. Calculation of reinforced-concrete structures for explosive and impact loads[M]. (in Russian), STT, Northampton, Tomsk, 2004.
[18] БЕЛОВ Н Н, ЮГОВ Н Т, АФАНАСЬЕВА С А, et al. Исследование процессов деформирования и разрушения хрупких материалов[J]. Механика Композиционных Материалов и Конструкций, 2001, 7(2): 131-142.
Shock-hugoniotrelationshipsofsandconsideringporosityevolution
GAO Fei1, 2, QIU Yanyu1, 2, WANG Mingyang1, 2, ZHANG Xianfeng1, CHENG Yihao2
(1. Ministerial Key Laboratory of ZNDY,Nanjing University of Science and Technology, Nanjing 210094, China;2. State Key Lab for Disaster Prevention & Mitigation of Explosion & Impact, PLA University of Science and Technology, Nanjing 210007, China)
Effects of porosity evolution on sand shock-hugoniot relationships under dynamic loading were investigated based on porous and hydrous characteristics of sand. Based on the incompressible hypothesis of sand matrix, using a single spherical pore equivalent model and the generalized Mises strength criterion, the porosity evolution equation of sand was derived. According to Hugoniot jump condition and Grüneisen-type state equation, the state equation of sand considering porosity dynamic compaction was deduced. The shock-hugonoit curves for sand matrix, dry sand and moist sand were gained by using the mixture-shock wave relationship and porosity evolution state equation. Results showed that the calculated shock-hugonoit curves for sand agree well with the available test data in literature; the porosity evolution state equation can more correctly reflect the dynamic response process of sand under dynamic loading.
sand; porosity evolution; Grüneisen-type equation of state; shock-hugoniot relationships
国家自然科学基金面上项目(51478466);国家自然科学基金青年项目(51508568);爆炸科学与技术国家重点实验室开放基金项目(KFJJ15-07M)
2016-01-26 修改稿收到日期:2016-07-28
高飞 男,博士生,1990年生
王明洋 男,教授,博士生导师,1966年生
E-mail:wmyrf@163.com
O383
: A
10.13465/j.cnki.jvs.2017.17.021

