黄土与地铁车站动力相互作用模型的水平位移及沉降分析
权登州, 王毅红, 叶 丹, 井彦林, 陈 苏
(1. 长安大学 建筑工程学院, 西安 710061; 2. 中国地震局地球物理研究所, 北京 100081)
黄土与地铁车站动力相互作用模型的水平位移及沉降分析
权登州1, 王毅红1, 叶 丹1, 井彦林1, 陈 苏2
(1. 长安大学 建筑工程学院, 西安 710061; 2. 中国地震局地球物理研究所, 北京 100081)
在黄土场地条件下进行土与地铁地下结构动力相互作用振动台试验。基于实测数据对黄土与地铁车站接触动土压力、模型地基竖向沉降及水平位移进行分析,对试验中模型地基地震破坏特点进行描述。结果表明:结构侧面顶部动土压力大于中部和下部,随输入峰值加速度的增大结构侧面土压力均增大;地震动较大时,地基层间剪切位移呈现顶部最大,底部次之,中部最小;地表沉降随输入峰值加速度的增加而增大,西安人工波作用下地表沉降大于松潘波和Taft波作用下沉降;结构上方地表沉降始终小于周围土层,表明结构发生相对上升运动;分析发现,结构顶、底动土压力差提供结构上升运动的内在动力。回归分析表明,地基水平相对位移与土层深度可用三次多项式拟合,两者之间具有较好的相关性。
黄土地区; 地铁车站; 振动台试验; 动土压力; 水平位移; 沉降分析
随着我国西部黄土地区地铁工程逐渐增多,黄土地区地铁地下结构的抗震性能及安全性评价日益受到密切关注[1]。由于黄土具有柱状节理、大孔隙、弱胶结的特殊结构性及对水的特殊敏感性[2],使得黄土地区震害相对其它土类要严重的多。动力、静力及浸水作用分别引起黄土震陷、压密及湿陷变形,黄土震陷变形大小与动力荷载相对于静力荷载及浸水作用的先后有密切关系。因此,黄土场地对地震作用十分敏感,开展黄土场地条件下地铁地下结构地震模拟振动台试验研究具有重要意义。
近年,国内外学者对地下结构地震反应特性开展了广泛深入的研究[3-6],Jafarzadeh等[7]进行了系列振动台试验,研究了埋地管线在均质和非均质场地中的地震反应,Amorosi等[8]对圆形隧道的地震响应进行了数值分析,Azadi等[9]基于FLAC 3D软件研究了可液化地基隧道的地震反应,Chian[10]研究了振动台试验中不同边界条件对模型结构上浮特性的影响,杨林德等[11]进行了软土地层中地铁车站及地铁车站与区间隧道接头结构的振动台模型试验;陈国兴等[12-13]在软弱场地、可液化土层等不同地质条件下进行了土-地铁地下结构动力相互作用大型振动台试验和数值模拟研究;刘晶波等[14]对砂土地基中地下结构进行了离心机振动台试验研究;刘妮娜等[15]对黄土自由场地及地裂缝场地中地铁隧道的地震反应进行了研究;秦立科等[16]通过三轴试验对非饱和黄土的动力本构模型进行了研究;赵占厂等[17]基于公路隧道衬砌现场测试,对黄土隧道受力性能进行了研究;张柯等[18]对地铁行车荷载作用下黄土地层震动响应和减震进行了研究,并对城市轨道交通隔振减震机理和措施进行了研究;刘建军等[19]对西安地区长周期地脉动进行了观测,分析了西安地区地下构造固有频率特性,推断了观测区地下软土层分布。除此之外,其他一些学者也对地铁地下车站、区间隧道等地下结构抗震进行了大量有益的探索。然而,基于土-结相互作用大型地震模拟振动台试验研究黄土场地及地铁车站地震反应还较少。
西安地铁是我国首次在黄土地区修建地铁工程。本文以西安地铁工程为背景,进行了黄土与地铁地下车站动力相互作用地震模拟振动台试验。基于实测数据对黄土与地铁车站接触动土压力、模型地基竖向沉降及水平位移进行了深入分析,对试验中模型地基地震破坏特点进行描述。研究结论可为黄土地区地铁车站、区间隧道及地下商业街等地下结构的抗震设计及相关理论研究提供可靠资料。
1 试验简介
1.1模型设计与制作
以西安地铁飞天路车站为原型结构制作模型,该地铁车站位于黄土台塬区,上覆土层厚3 m,为典型的两层双跨矩形断面结构,车站宽19.2 m,高14.01 m,左右跨对称布置;上、下层侧墙厚度均为0.7 m;上、下层净高分别为5.65 m和6.16 m;顶板、中板及底板厚度分别为0.8 m、0.4 m及1.0 m;板构件与墙、柱连接处做了加腋处理。根据Bockingham π定理,选取长度、弹性模量及加速度为基本物理量,并充分考虑试验系统的台面尺寸、动力性能、承载吨位及其它配套设备性能等制约,确定模型体系的相似关系见表1。
根据相似设计确定模型结构尺寸;采用微粒混凝土及镀锌钢丝分别模拟原型结构混凝土及钢筋,微粒混凝土弹性模量为6 602 MPa;按照原型与模型构件弯矩、剪力等效及施工可操作性原则,确定模型结构中钢筋布置。同时,在模型结构中黏贴铅块以实现附加人工质量。
振动台试验使用的叠层剪切模型土箱净尺寸为3.5 m×2.0 m×1.7 m,采用15层叠层方钢管框架并辅之以双侧面钢板约束的方案,在水平振动方向形成可自由滑动的边界,该叠层剪切模型土箱能较好地消除边界上地震波反射或散射效应[20]。试验中黄土取自飞天路车站施工基坑,制备模型地基时,将黄土分层装入模型土箱,按原型场地土天然含水量和密度控制模型地基含水量及密度,黄土样的基本物理指标见表2。

表1 模型相似常数

表2 黄土材性参数
1.2传感器布置与加载方案
基于ABAQUS大型非线性有限元分析平台,采用有限元-无限元耦合的建模方法,对黄土场地中地铁车站的地震响应进行了数值模拟[21]。根据数值模拟结果、模型尺寸及试验条件,确定振动台试验中位移和动土压力传感器布置方案如图1所示。图中L1~L5为位移传感器;G1与G2为激光位移计;P1~P7为土压力传感器。本试验采用的激振系统为美国MTS公司生产的水平单向高性能地震模拟振动台,台面尺寸为3.36 m×4.86 m,最大载重量25 t,最大加速度±1.0 g。为了研究地震动特性对黄土场地地铁车站模型体系地震反应的影响,分别选择Taft波、松潘波和西安人工波作为输入地震动,其加速度时程及傅里叶谱如图2所示,加载工况见表3。
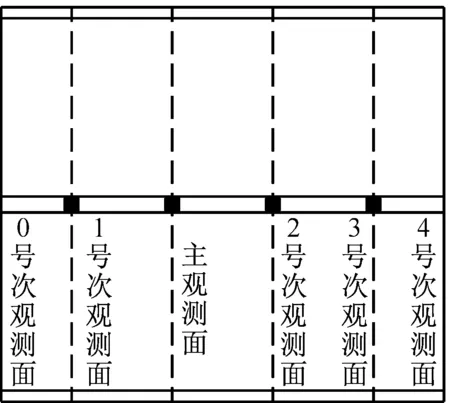
(a) 模型结构观测断面位置

(b) 主观测面位移传感器布置 (mm)
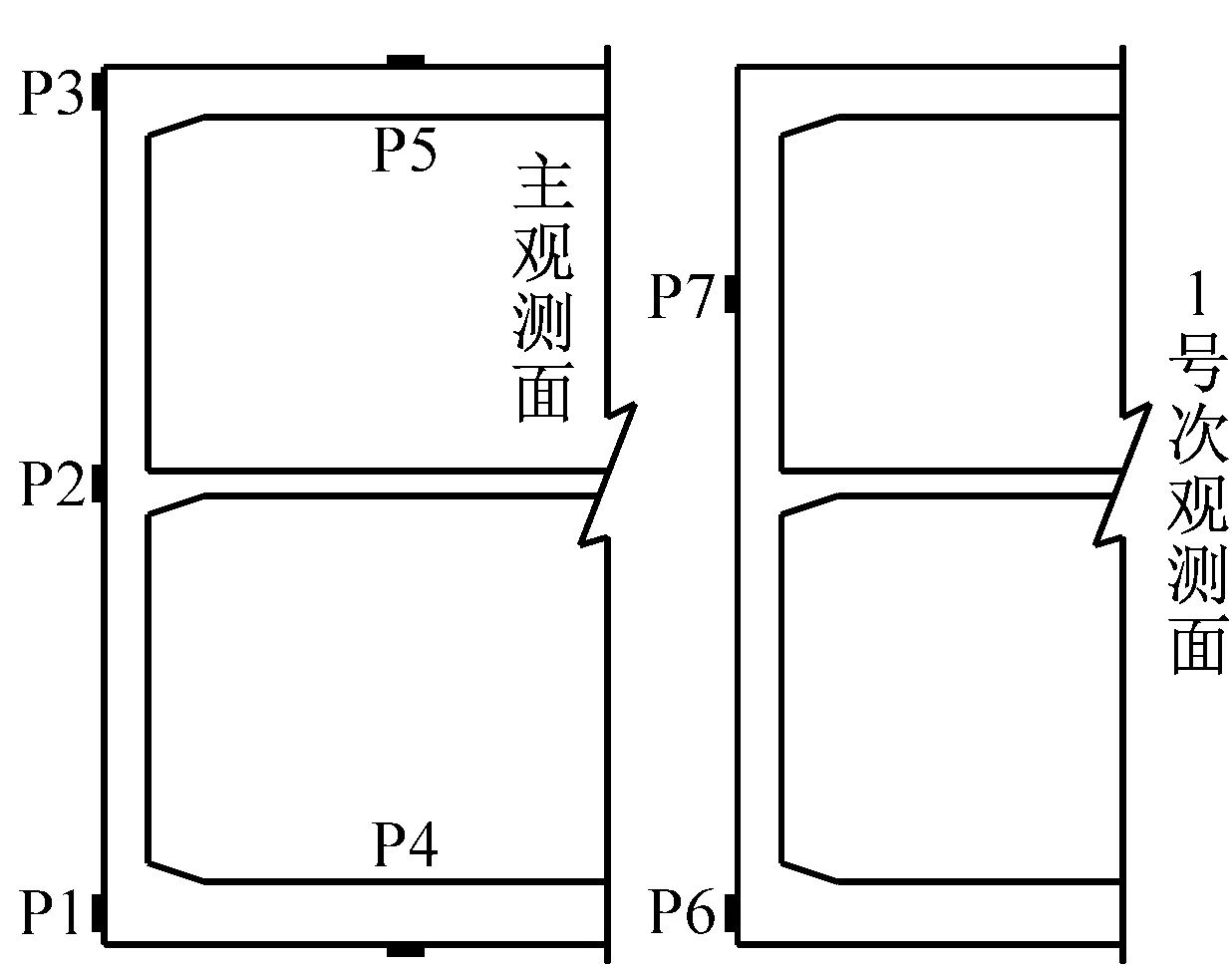
(c) 动土压力传感器布置

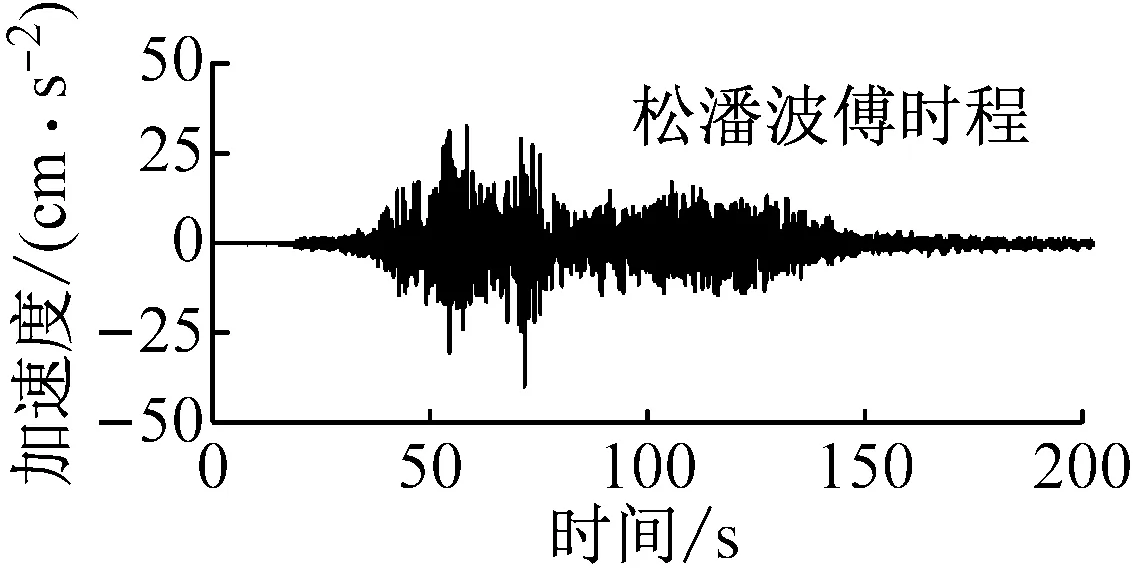
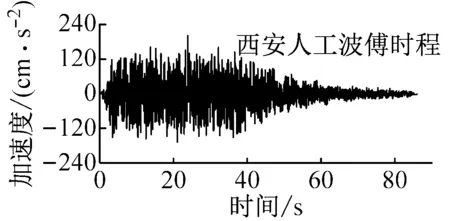

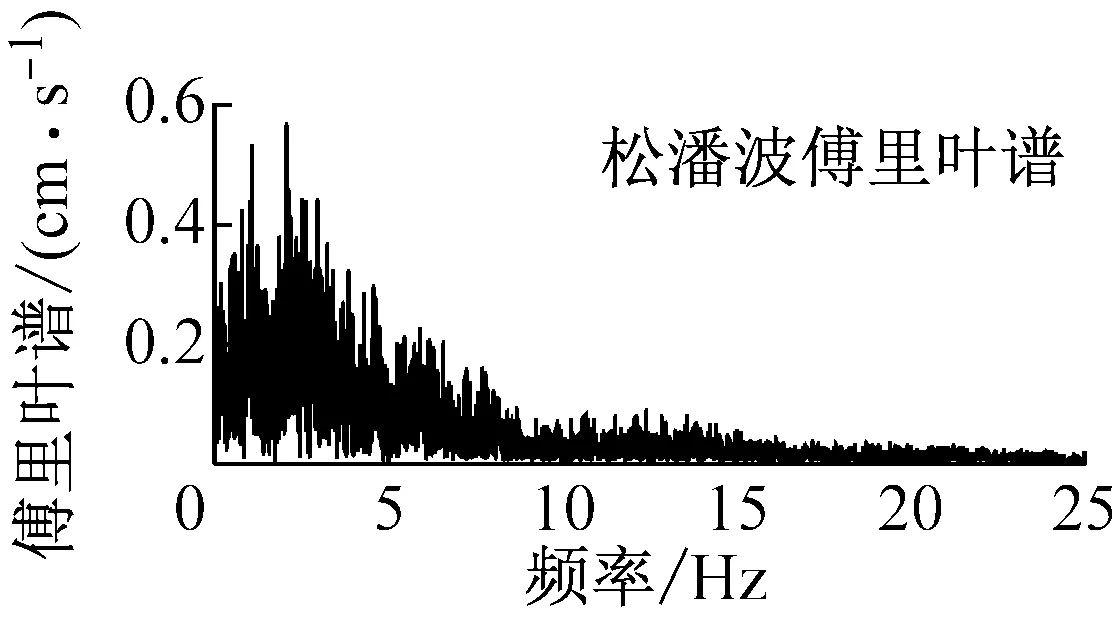
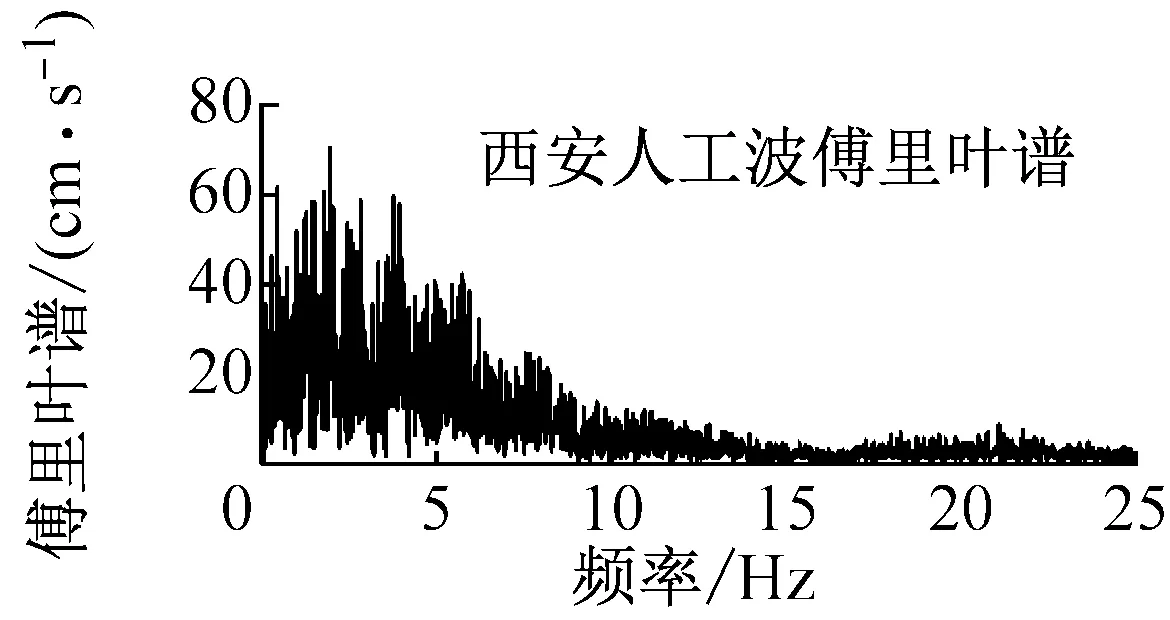
图2 输入地震动的加速度时程及傅里叶谱
2 试验结果分析
2.1黄土与地铁车站接触动土压力
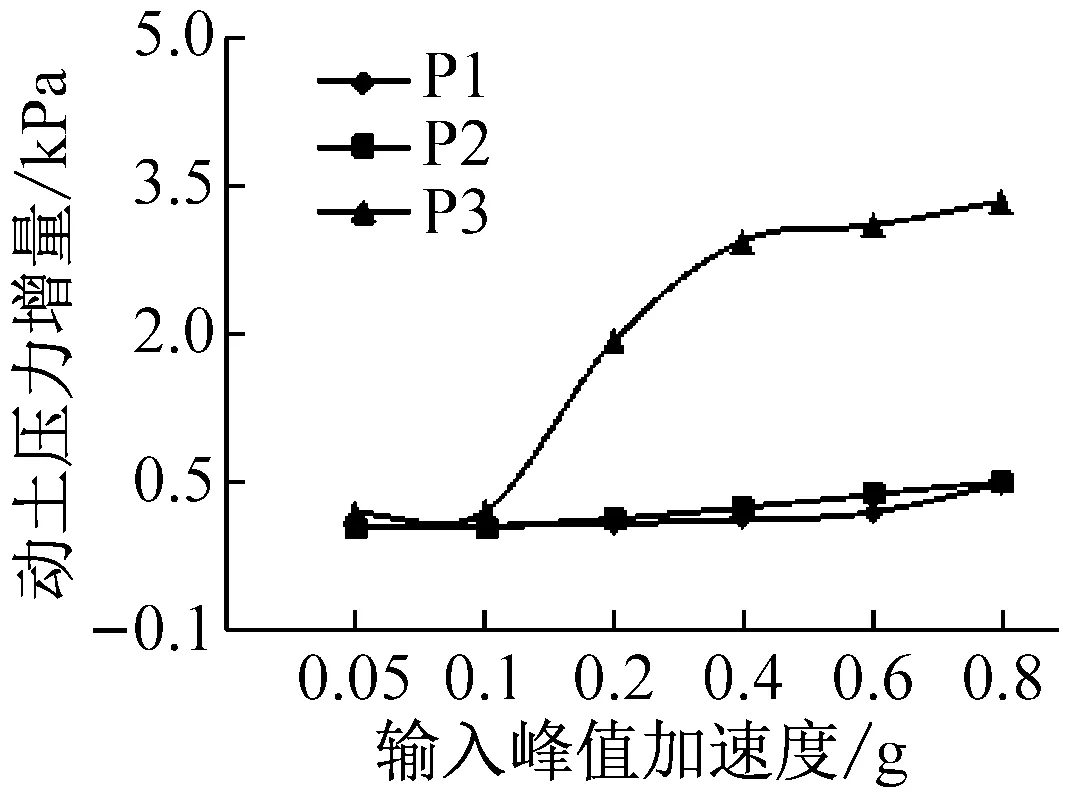
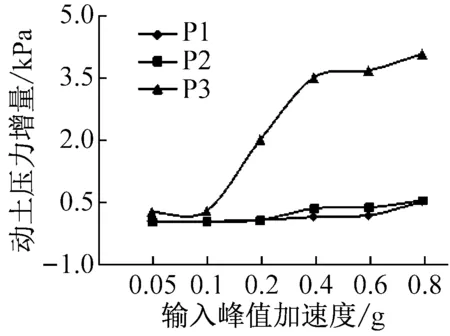
地铁车站主观测断面内侧墙不同高度处动土压力增量如图3所示(图中字母和数字组合代表工况或测点,下同)。由图3(a)可知,输入相同峰值加速度时,地铁车站侧墙动土压力增量均随测点高度增加而增大;侧墙顶部动土压力增量随输入峰值加速度增加显著增大。这是由于随着测点高度增加,周围土体地震动力反应增强,土层剪切变形增大,土结动力相互作用下更剧烈,从而动土压力增量较大。由图3(b)~(c)可知,随着输入峰值加速度增加,地震动所蕴含的能量越多,土-结动力相互作用逐渐增强,从而地铁车站侧面各测点的动土压力增量均增大。同时发现,地铁车站侧墙底部和中部测点P1和P2动土压力增量较小且较接近,其随输入峰值加速度增加而增长较缓慢;结构侧墙顶部测点P3动土压力增量相对较大,且随输入峰值加速度增加呈现出缓增-急增-缓增的变化规律:当输入峰值加速度不大于0.1 g时,动土压力增量增长较缓慢,当输入峰值加速度大于0.1 g且小于0.4 g时,动土压力增量急剧增长,当输入峰值加速度大于0.4 g时,动土压力增量又缓慢增长。上述分析表明,地铁车站侧墙顶部动土压力增量显著大于中部和底部,且随输入峰值加速度增大,侧墙顶部动土压力增量有明显增大。
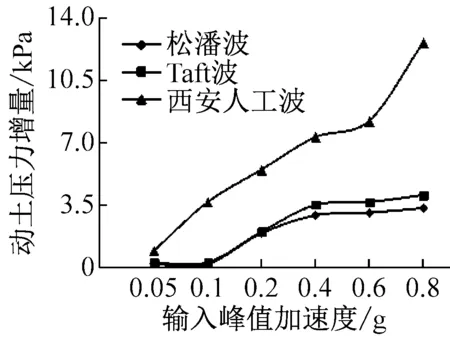
由图3(d)~(f)可知,输入峰值加速度较小时,不同频谱特性地震动作用下地铁车站侧墙底部和中部测点P1和P2动土压力增量较接近且规律性不明显;输入0.8 g峰值加速度时,不同频谱特性地震动作用下P1和P2动土压力增量呈现出相同规律,即动土压力增量在西安人工波作用下较大,Taft波作用下居中,松潘波作用下较小。在较小地震动作用下,由于侧墙底部和中部测点P1和P2动土压力增量较小,受土压力盒测量精度影响,不同频谱特性地震动作用下动土压力增量规律性不明显;在强震中P1和P2动土压力增量有所增大,不同频谱特性地震动作用下其动土压力增量呈现出明显规律性,由于西安人工波低频成分较松潘波和Taft波发育,而地铁车站周围土体对输入地震动低频成分较敏感,在西安人工波作用下结构周围土体地震动力反应较强,土-结动力相互作用较剧烈,因此,动土压力增量呈现出西安人工波作用下较大,松潘波和Taft波作用下相对较小。地铁车站侧墙顶部测点P3动土压力增量相对较大,不同频谱特性地震动作用下其动土压力增量始终表现为西安人工波作用下较大,松潘波和Taft波作用下相对较小;此外,随输入峰值加速度增加,不同频谱特性地震动作用下P3动土压力增量的差异更加显著。综上所述,不同频谱特性地震动作用下结构侧面动土压力增量呈现出西安人工波作用下较大,松潘波和Taft波作用下相对较小;且随输入峰值加速度增加及测点高度增加,结构侧面动土压力增量均对输入地震动频谱组成特性更加敏感。
(a) 西安人工波下动土压力
(b) 松潘波下动土压力
(c) Taft波下动土压力

(d) P1 动土压力

(e) P2动土压力
(f) P3动土压力
振动台试验中,在主观测断面地铁车站底板下表面及顶板上表面分别布置土压力盒P4和P5,1号次观测断面下层侧墙底部及上层侧墙中部分别布置土压力盒P6和P7,不同观测断面内结构动土压力增量见表4。由表可知,底板下表面测点P4动土压力增量显著大于顶板上表面测点P5。由于结构底板以下土体同时承受结构自重及上覆土层重,在地震动力作用下土与结构相互作用力较大,从而底板下表面测点P4动土压力增量较大。同时发现,当输入地震动小于0.4 g时,随输入峰值加速度增加P4动土压力增量逐渐增大,当输入峰值加速度大于0.4 g时,P4动土压力增量有所减小;不同频谱特性地震动作用下,P4动土压力增量呈现出西安人工波作用下较大,松潘波和Taft波作用下相对较小。由于地铁车站埋深较浅,上覆土层较薄,结构顶板上表面测点P5动土压力增量相对较小;除个别工况外,随输入峰值加速度增加P5动土压力增量逐渐增大;不同频谱特性地震动作用下P5动土压力增量无明显规律。
对比表4中1号次观测断面内P6及P7动土压力增量可知,输入峰值加速度小于0.4 g时,上层侧墙中部P7动土压力增量小于下层侧墙底部P6;输入峰值加速度大于0.4 g时,P7动土压力增量则大于P6。在较小地震动作用下,土-结动力相互作用较弱,1号次观测断面内各测点动土压力增量较小,由于P6测点与结构底板同高度,P7测点位于上层侧墙中部,因此P7测点处水平刚度较小,在土-结动力相互作用过程中会产生相对较大水平位移,从而使P7动土压力增量较小;在较大地震动作用下,土-结动力相互作用较强,1号次观测断面内各测点动土压力增量相对较大,而上层侧墙中部P7测点水平位移有限,此时由于P7测点高度较大,周围土体地震反应较强,土层剪切变形较大,土-结动力相互作用更剧烈,从而动土压力增量增大。
对比表4中不同观测断面内下层侧墙底部测点动土压力增量,发现1号次观测断面内P6动土压力增量始终大于主观测断面内P1动土压力增量。这主要受两方面因素影响:其一,由于地铁车站纵向端部土-结动力相互作用较强,1号次观测断面距结构端部较近,受结构端部影响其内P6测点的动土压力增量较大;其二,由于在施工及安装传感器过程中,模型地基不可避免的产生一定程度密度不均匀性,不同观测断面处土-结动力相互作用强度存在一定差异,从而使1号次观测断面内P6动土压力增量较大。
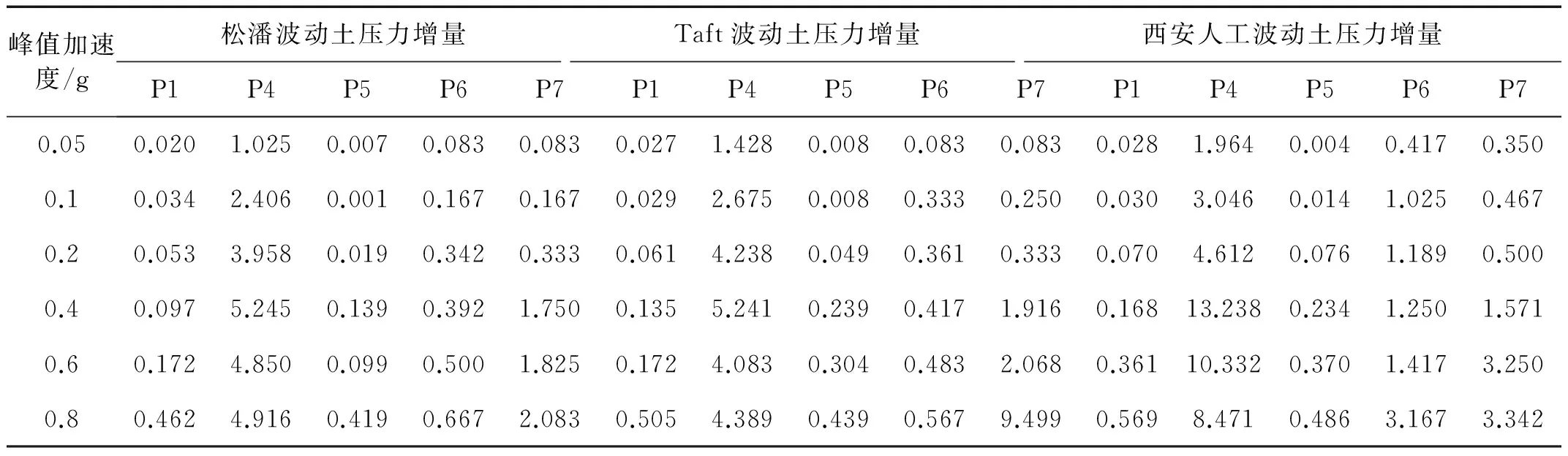
表4 不同观测断面的土压力增量
2.2模型地基竖向沉降
布置于模型地表的激光位移计G1和G2测得了模型体系不同位置处的竖向沉降。输入不同峰值加速度时,松潘波、Taft波和西安人工波作用下,模型地基表面竖向沉降见表5。由表可知,除个别工况外,地基表面各测点的竖向沉降随输入地震动峰值加速度的增大而增大;输入相同峰值加速度时,在不同频谱组成地震动作用下地基表面各测点竖向沉降基本呈现出西安人工波作用下较大,松潘波和Taft波作用下较小。
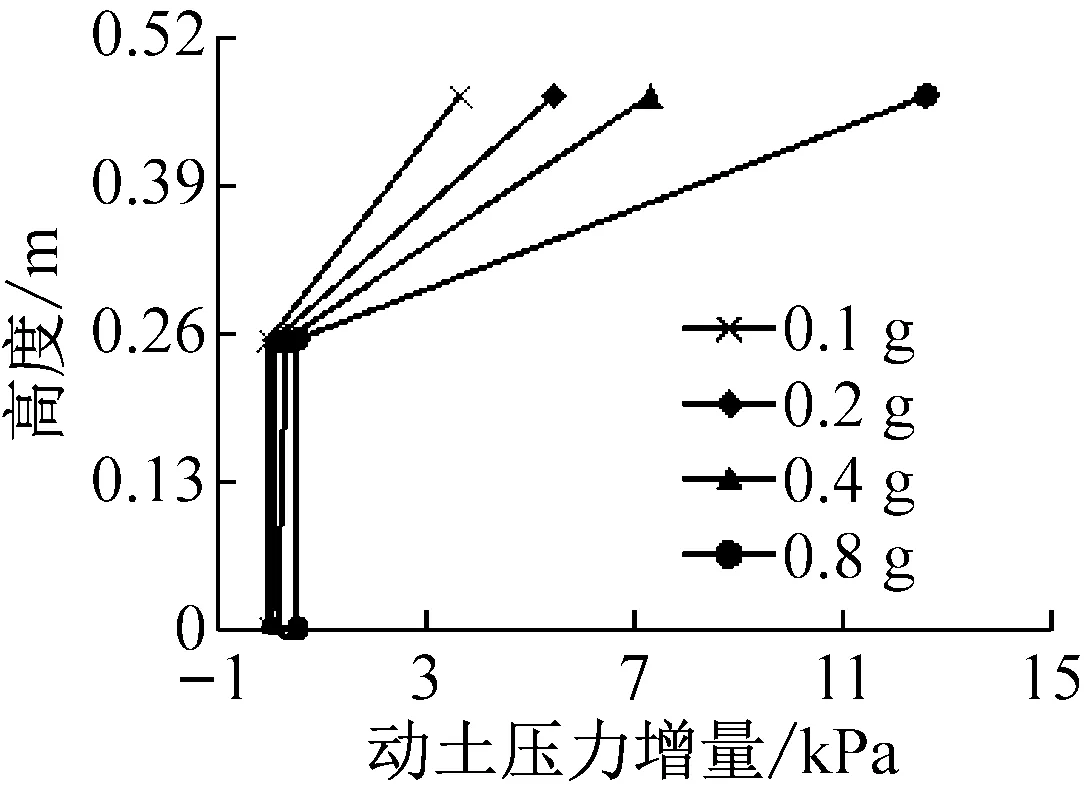
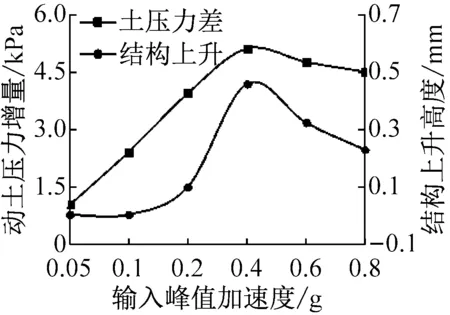
实测沉降数据表明,地铁车站结构上方地基表面测点G2的竖向沉降始终小于远离结构处地基表面测点G1的竖向沉降,这是由于地铁车站结构与周围土体竖向运动不一致引起的沉降反应差异。在地震动作用下,由于G2测点竖向沉降小于G1测点,因此地铁车站结构相对周围土体产生了上升运动,上升幅度可用G1与G2侧点竖向沉降差表示,不同峰值加速度的各类地震动作用下,结构上升高度见表5。由表可知,地铁车站结构上升高度均具有如下规律:在较小地震动时,随着输入峰值加速度增大,结构上升高度逐渐增大;当输入峰值加速度为0.4 g时,结构上升高度最大;在较大地震动时,随着输入峰值加速度增大,结构上升高度有所减小。为研究地铁车站结构上升运动机理,将表3中结构顶底部动土压力增量与表4中结构上升高度进行对比分析发现,结构底板下表面测点P4的动土压力增量显著大于顶板上表面测点P5,且P4与P5测点的动土压力增量差与结构上升高度均具有相似的变化规律:在较小地震动时,P4与P5测点的动土压力增量差随着输入峰值加速度增大而逐渐增大;当输入峰值加速度为0.4 g时,P4与P5测点的动土压力增量差达到最大值;在较大地震动时,P4与P5测点的动土压力增量差随着输入峰值加速度增大则有所减小,如图4所示。因此,可以推断结构底部与顶部动土压力增量差是地铁车站结构竖向运动的内在动力。
2.3模型地基水平位移
为得到模型地基水平位移反应,在叠层剪切模型土箱侧边布置5个位移测点。不同工况下,模型地基表面测点L5水平位移时程如图5所示。由图可知,松潘波和西安人工波作用下,地表水平位移时程较饱满,曲线与坐标横轴交点较密集,Taft波作用下,地表水平位移时程较松散,曲线与坐标横轴交点较稀疏。不同特性地震动作用下,模型地基中各测点在正负两个方向水平位移幅值如图6所示。西安人工波作用下,随土层深度减小,地基中正负两个方向水平位移幅值均增大;随输入峰值加速度增大,其正负两个方向上水平位移幅值亦增大,且随埋深减小其增加速度越快;同时发现,地基中正负两个方向水平位移幅值分布并不对称,随输入峰值加速度增大,地表负向水平位移幅值增加的幅度逐渐大于正向,这是由于地震动加速度时程正负两个方向幅值不对称,具有一定的方向性。松潘波作用下,随输入峰值加速度增大,地基中正负两个方向上水平位移幅值均增大;在较小地震动作用下,地基中正负两个方向水平位移幅值随土层深度减小变化较小,在较大地震动作用下,地基中正负两个方向水平位移幅值随土层深度减小出现微幅增加。Taft波作用下,随输入峰值加速度增大,地基中正负两个方向上水平位移幅值均增大;随土层深度减小,其正负两个方向水平位移幅值变化较小。松潘波和Taft波作用下,地基中正负两个方向上水平位移幅值差异较小,未表现出明显的方向性。
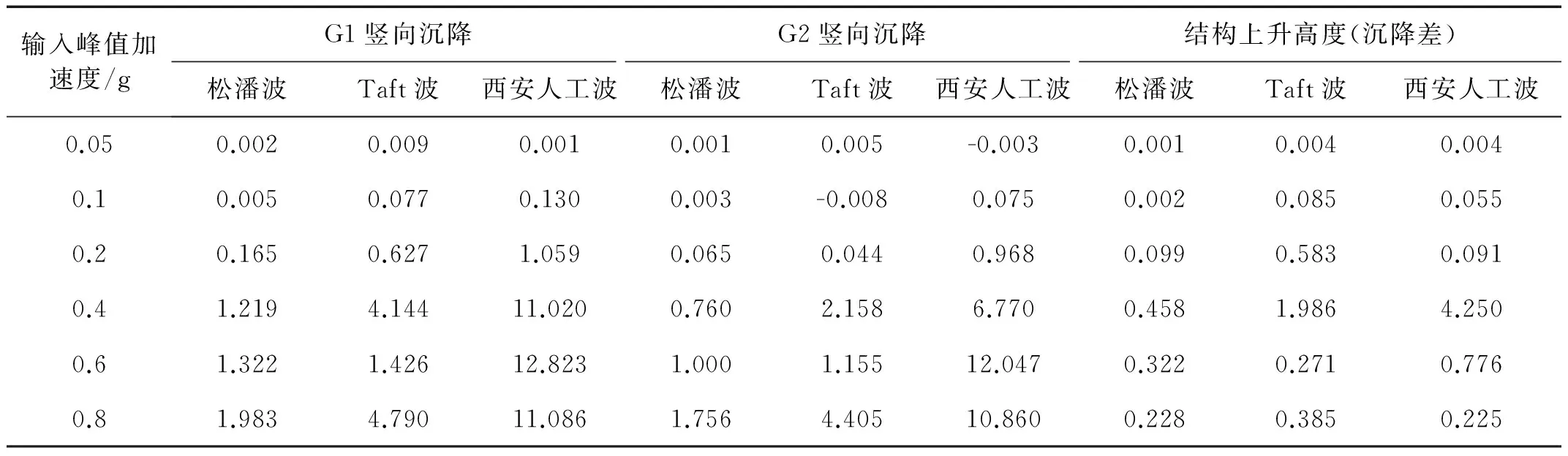
表5 不同工况下模型体系的竖向沉降
(a) 松潘波

(b) Taft波

(c) 西安人工波
模型地基表面与底面发生最大剪切变形时刻,地基内各测点相对于底部的水平相对位移如图7所示。由图可知,在较小地震动作用下,随土层深度减小,地基内水平相对位移基本呈现出先增大后减小再增大的波浪式变化,且不同频谱特性地震动作用下水平相对位移相差不大,沿深度分布在较窄的带状区域内。在较大地震动作用下,随土层深度减小,地基内水平相对位移逐渐增大,且其曲线均出现明显反弯点,曲线斜率呈现出顶部最小,底部次之,中部最大的形态特征,因此,模型地基层间剪切位移具有顶部最大,底部次之,中部最小的反应规律。此外,输入较大峰值加速度时,不同频谱特性地震动作用下地基内相同深度处水平相对位移显著不同,均呈现出西安人工波作用下较大,松潘波和Taft波作用下较小。这是由于西安人工波低频成分较松潘波和Taft波发育,土体基频较低,对低频成分较敏感,从而表现为西安人工波作用下水平相对位移反应较大。

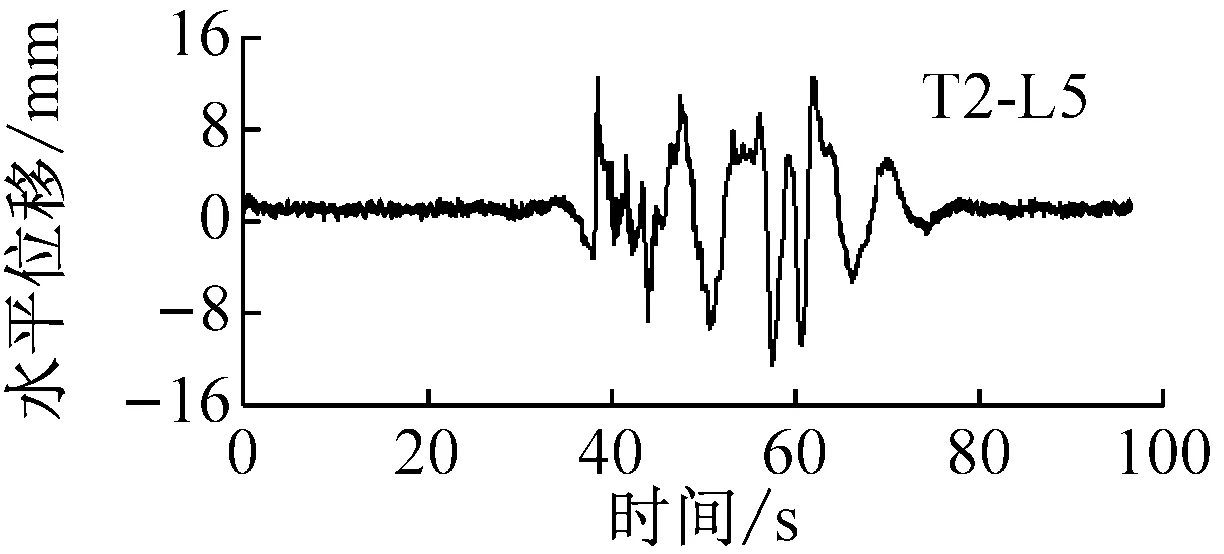
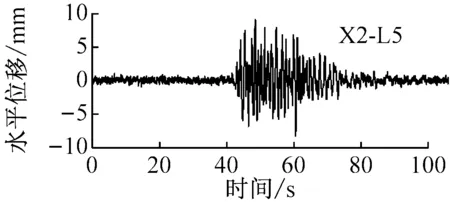

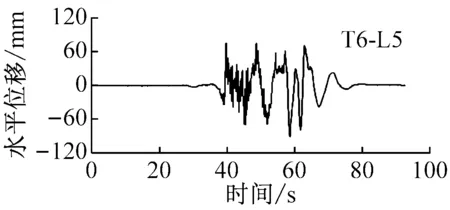
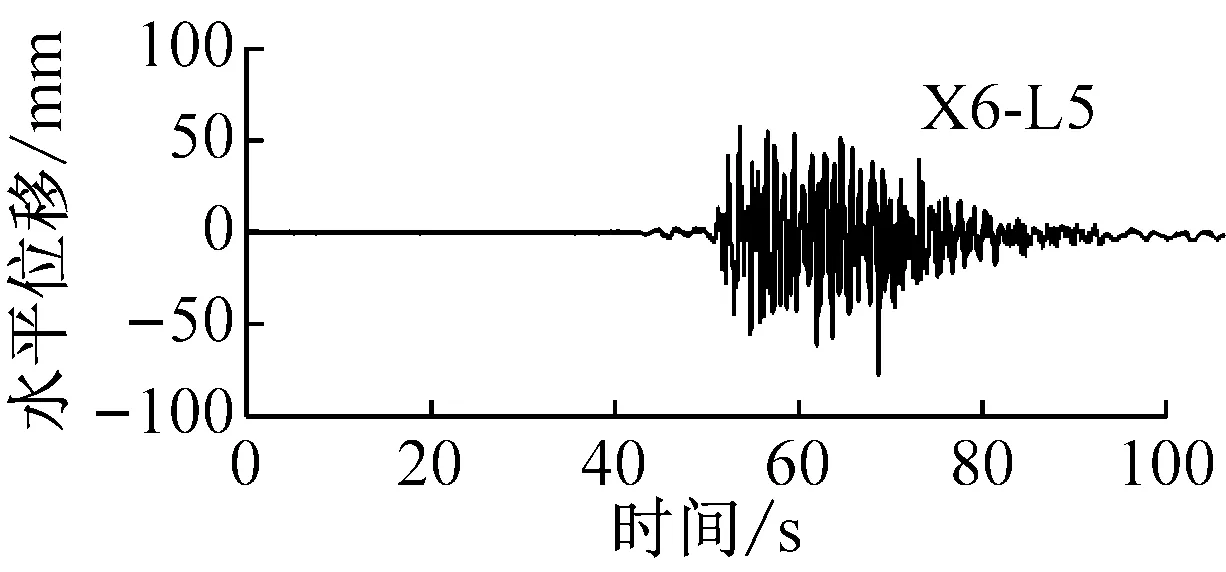
图5 模型地基水平位移反应时程曲线

(a) 松潘波

(b) Taft波

(c) 西安人工波
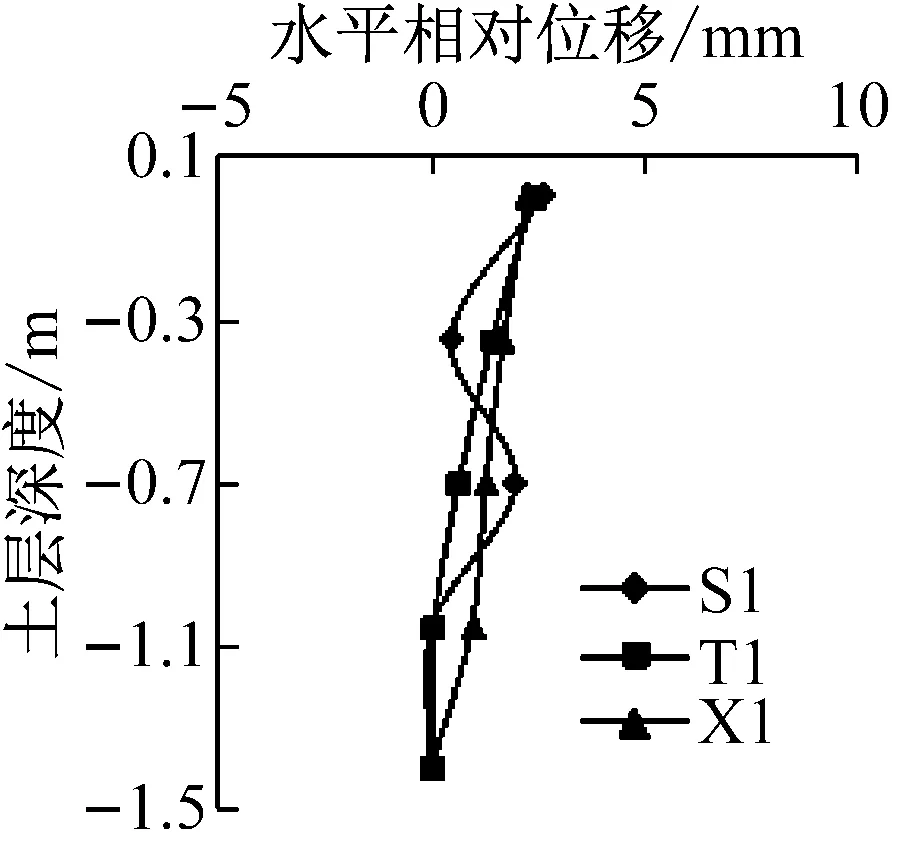

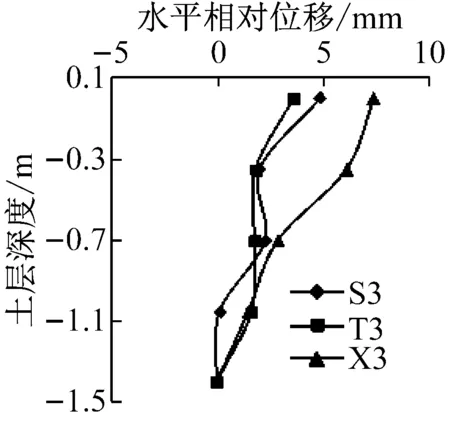
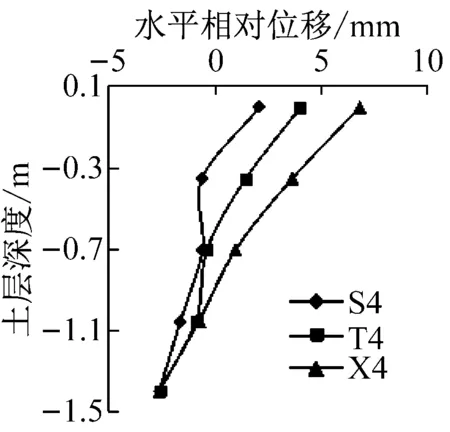
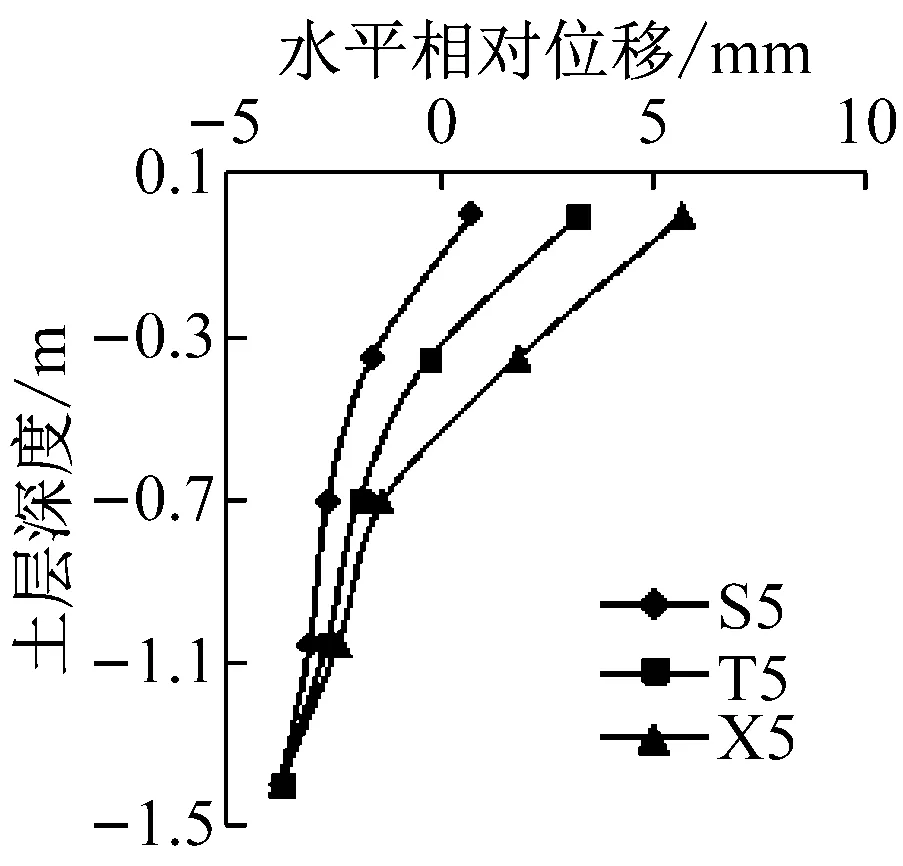
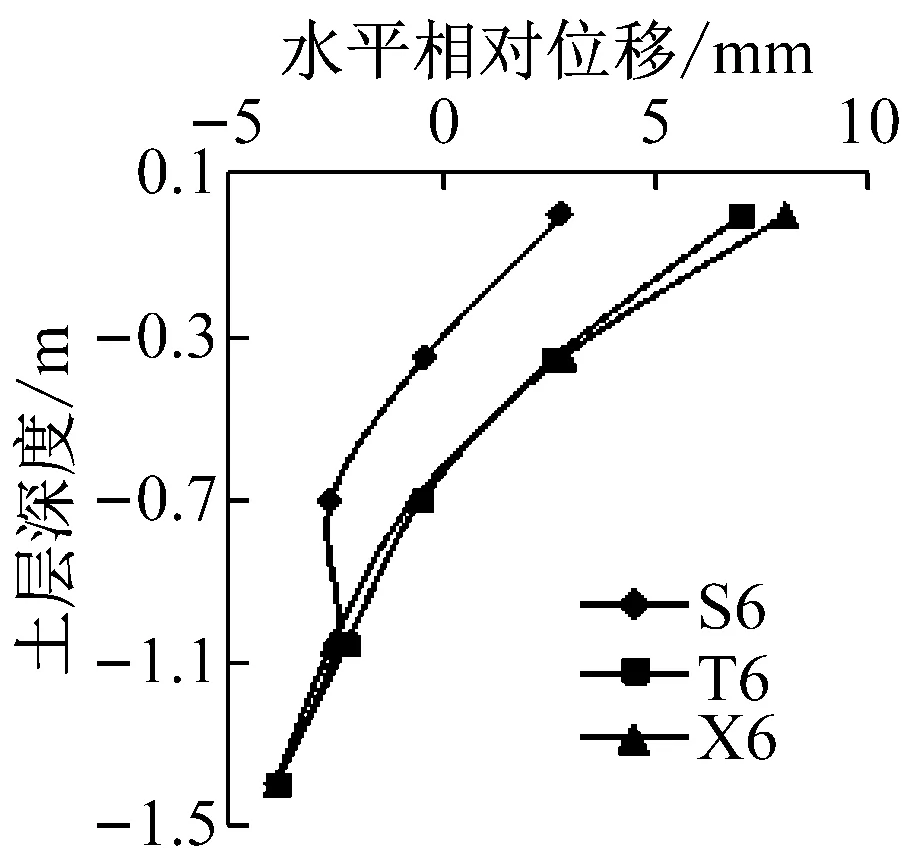
图7 模型地基水平相对位移分布
输入较大峰值加速度时,模型地基表面与底面发生最大剪切变形时刻,不同频谱特性地震动作用下模型地基内水平相对位移沿深度的分布较相似。为了研究地基水平相对位移与土层深度之间关系,将输入相同峰值加速度时,不同特性地震动作用下地基内水平相对位移取平均值,并采用非线性回归分析对水平相对位移平均值与土层深度进行拟合。输入不同峰值加速度时,水平相对位移与土层深度非线性拟合曲线如图8所示。由图可知,模型地基水平相对位移与土层深度之间有较好的相关性,可采用形如式(1)的三次多项式表示。输入不同峰值加速度时,水平相对位移与土层深度之间拟合参数及相关系数见表6。
δ=Ah3+Bh2+Ch+D
(1)
式中:δ为模型体系表面与底面发生最大剪切变形时刻的水平相对位移,单位为mm;h为土层深度,单位为m;
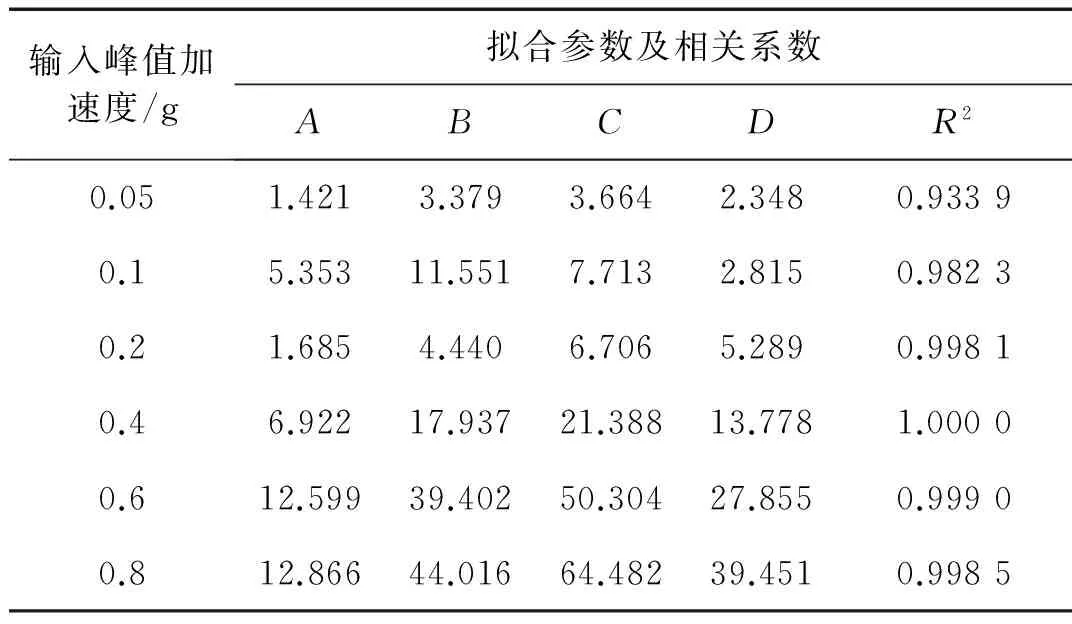
表6 水平相对位移拟合曲线参数
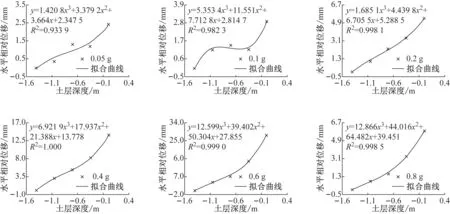
图8 模型地基水平相对位移拟合曲线
A,B,C与D为拟合参数。
3 模型地基震害
振动台试验中,在各工况加载结束后,对模型地表裂缝发育进行观察。X4工况完成时,地表位于模型结构侧墙位置开始出现沿垂直于振动方向延伸的纵向裂缝。X5工况结束时,地表位于模型结构端头位置开始出现沿振动方向延伸的横向裂缝,同时,纵向裂缝发育更为明显。X6工况结束时,地表沿模型结构四周的纵、横向裂缝快速发展,并相互贯通形成闭合的主裂缝,且以主裂缝为源头出现数条枝裂缝向远离结构方向蔓延。X7工况过程中,地表闭合主裂缝外部模型地基产生了较大竖向沉降,模型结构所在位置发生了明显的相对上升运动,如图9(a);同时,主裂缝周边的枝裂缝发育较快,枝裂缝数量增多,裂缝宽度更大,并延伸的更远,如图9(b)所示。试验结束后,地表裂缝最宽处达1.5 cm,竖向沉降差最大3.2 cm,如图9(c)所示。

(a) 地表宏观震害

(b) 主裂缝与支裂缝

(b) 地表竖向沉降
4 结 论
本文开展了黄土与地铁车站动力相互作用大型地震模拟振动台试验,基于实测数据对黄土与地铁车站接触动土压力、模型地基竖向沉降及水平位移进行分析,研究结论可为黄土地区地铁地下结构抗震设计及相关理论研究提供重要参考,主要结论如下:
(1) 地铁车站侧墙顶部动土压力增量大于中部和底部;随输入峰值加速度增大,结构侧墙动土压力增量均增大;不同频谱特性地震动作用下结构侧墙动土压力增量呈现出西安人工波作用下较大,松潘波和Taft波作用下相对较小,且随输入峰值加速度增加及测点高度增加结构侧墙动土压力增量均对输入地震动频谱组成更加敏感。
(2) 除个别工况外,地表测点竖向沉降随输入峰值加速度增加而增大;不同频谱特性地震动作用下,地表测点竖向沉降基本呈现出西安人工波作用下较大,松潘波和Taft波作用下较小。
(3) 分析发现,结构底部P4及顶部P5动土压力增量的差值与结构上升高度具有相同的变化规律:当地震动较小时,其值随输入峰值加速度增加而增大;在0.4 g地震动作用下其值最大;当地震动较大时,其值有所减小。因此,可以推断结构底部与顶部动土压力增量差是地铁车站竖向上升运动的内在动力。
(4) 随输入峰值加速度增大,模型地基内水平位移反应幅值均增大;在较大地震动作用下,地基水平相对位移随土层深度变化曲线呈现出明显的反弯点,曲线斜率呈现出顶部最小,底部次之,中部最大的形态特征,因此,模型地基层间剪切位移具有顶部最大,底部次之,中部最小的反应规律。
(5) 非线性回归分析表明,模型地基水平相对位移与土层深度之间具有较好的相关性,均可采用三次多项式拟合。因此,在黄土地区地铁地下结构抗震设计中,采用反应位移法计算地震作用时可考虑使用多项式表述自由场地水平相对位移沿土层深度的分布规律,其具体应用还需进一步研究验证。
[1] 权登州, 王毅红, 井彦林,等.黄土地区地铁车站数值模型及测试位置研究[J]. 震灾防御技术, 2015, 10(1): 108-115.
QUAN Dengzhou, WANG Yihong, JING Yanlin, et al. Numerical model and measuring position for subway stations in loess area[J]. Technology for Earthquake Disaster Prevention, 2015, 10(1): 108-115.
[2] 王志杰, 骆亚生, 杨永俊. 不同地区非饱和黄土动力结构性研究[J]. 岩土力学, 2010, 31(8): 2459-2464.
WANG Zhijie,LUO Yasheng,YANG Yongjun. Study of dynamic structural characteristics of unsaturated loesses in different regions[J]. Rock and Soil Mechanics, 2010, 31(8): 2459-2464.
[3] VARGHESE R M, LATHA G M. Shaking table tests to investigate the influence of various factors on the liquefaction resistance of sands[J]. Nat Hazards, 2014, 73:1337-1351.
[4] LANZANO G, BILOTTA E, RUSSO G, et al. Centrifuge modeling of seismic loading on tunnels in sand[J]. Geotechnical Testing Journal, 2012,35:1-16.
[5] CHEN Guoxing, WANG Zhihua, ZUO Xi, et al. Shaking table test on the seismic failure characteristics of a subway station structure on liquefiable ground[J]. Earthquake Engineering & Structural Dynamics, 2013, 42:1489-1507.
[6] CHEN Guoxing, CHEN Su, ZUO Xi, et al. Shaking-table tests and numerical simulations on a subway structure in soft soil[J]. Soil Dynamic and Earthquake Engineering, 2015, 76:13-28.
[7] JAFARZADEH F, FARAHI JAHROMI H, et al. Investigating dynamic response of a buried pipeline in sandy soil layer by 1G shaking table test[J]. International Journal of Civil Engineering, 2010,8(2): 107-124.
[8] AMOROSI A, BOLDINI D. Numerical modelling of the transverse dynamic behavior of circular tunnels in clayey soils[J]. Soil Dynamics and Earthquake Engineering, 2009, 29(6):1059-1072.
[9] AZADI M, MIR MOHAMMAD HOSSEINI S M. Analyses of the effect of seismic behavior of shallow tunnels in liquefiable grounds[J]. Tunnelling and Underground Space Technology, 2010,25(5): 543-552.
[10] CHIAN S C. Effect of buried depth and diameter on uplift of underground structures in liquefied soils[J]. Soil Dynamics and Earthquake Engineering, 2012(41):181-190.
[11] 杨林德, 季倩倩, 郑永来, 等. 软土地铁车站结构的振动台试验[J]. 现代隧道技术, 2003, 40(1): 7-11.
YANG Linde, JI Qianqian, ZHENG Yonglai, et al. Shaking table test on metro station structures in soft soil[J]. Modern Tunnelling Technolog, 2003, 40(1): 7-11.
[12] 陈国兴, 左熹, 王志华, 等. 近远场地震作用下液化地基上地铁车站结构动力损伤特性的振动台试验[J].土木工程学报,2010,43(12):120-126.
CHEN Guoxing, ZUO Xi, WANG Zhihua, et al. Large scale shaking table test study of the dynamic damage behavior of subway station structures in liquefiable foundation under near-fault and far-field ground motions[J]. China Civil Engineering Journal, 2010,43(12):120-126.
[13] CHEN Guoxing, CHEN Su, ZUO Xi, et al. Shaking-table tests and numerical simulations on a subway structure in soft soil[J]. Soil Dynamic and Earthquake Engineering, 2015, 76: 13-28.
[14] 刘晶波,刘祥庆,王宗纲,等土-结构动力相互作用系统离心机振动台模型试验[J]. 土木工程学报, 2010,43(11): 114-121.
LIU Jingbo, LIU Xiangqing, WANG Zonggang, et al. Dynamic centrifuge model test of a soil-structure interaction system[J]. China Civil Engineering Journal, 2010,43(11): 114-121.
[15] 刘妮娜. 地裂缝环境下的地铁隧道-地层地震动力相互作用研究[D]. 西安:长安大学,2010: 4-9.
[16] 秦立科. 非饱和黄土动力本构模型及其在地铁车站地震反应分析中的应用[D]. 西安: 长安大学, 2010: 1-16.
[17] 赵占厂, 谢永利, 杨晓华,等. 黄土公路隧道衬砌受力特性测试研究[J]. 中国公路学报, 2004, 17(1): 160-165.
ZHAO Zhanchang, XIE Yongli, YANG Xiaohua, et al. Observation research on the mechanical characteristic of highway tunnel lining in loess[J]. China Journal of Highway and Transport, 2004, 17(1): 160-165.
[18] 张柯, 吴敏哲. 地铁行车荷载作用下黄土地层的震动响应和沉降[D]. 西安: 西安建筑科技大学, 2011: 1-15.
[19] 刘建军, 李跃明, 车爱兰. 长周期地脉动观测在西安地区地下构造调查中的应用[J]. 西北地震学报, 2011, 33(增刊1): 403-412.
LIU Jianjun, LI Yueming, CHE Ailan. Application of long period microtremor observation on underground structure investigation in Xi’an area[J]. Northwestern Seismological Journal, 2011, 33(Sup1): 403-412.
[20] 陈国兴,王志华,左熹,等. 振动台试验叠层剪切型土箱的研制[J]. 岩土工程学报,2010,32(1): 89-97.
CHEN Guoxing, WANG Zhihua, ZUO Xi, et al. Development of laminar shear soil container for shaking table tests[J]. Chinese Journal of Geotechnical Engineering, 2010,32(1): 89-97.
[21] 权登州, 王毅红, 井彦林,等.黄土地区地铁车站数值模型及测试位置研究[J]. 震灾防御技术, 2015, 10(1): 108-115.
QUAN Dengzhou, WANG Yihong, JING Yanlin, et al. Numerical model and measuring position for subway stations in loess area[J]. Technology for Earthquake Disaster Prevention, 2015, 10(1): 108-115.
Horizontaldisplacementandsettlementanalysisforloess-subwaystationdynamicinteractionmodel
QUAN Dengzhou1, WANG Yihong1, YE Dan1, JING Yanlin1, CHEN Su2
(1. School of Civil Engineering, Chang’an University, Xi’an 710061, China;2. Institute of Geophysics, China Seismological Bureau, Beijing 100081, China)
A series of shaking table tests were performed for a loess-subway station dynamic interaction model. The dynamic soil pressure between loess and subway station, the horizontal displacement and vertical settlement of the model foundation were analysed, the seismic damage features of the model foundation were described after the tests. The results showed that the dynamic soil pressure of the structure’s side face increases with increase in input PGA, it is higher at the side top than that at the side middle and bottom; under higher PGA foundation motion, the shear displacement between soil layers is larger at the foundation top than that at the bottom, while the shear displacement at the foundation middle is smallest; the settlement of the ground surface increases with increase in input PGA, and the peak value of settlement is larger under Xi’an artificial wave than that under Songpan wave and Taft one; the settlement above the subway station is always smaller than that surrounding soils, the subway station uplifts relatively; the difference between dynamic soil pressures at the top and bottom of the subway station provides an uplifting force; meanwhile, after using the nonlinear regression analysis method, the relationship between the relative horizontal displacement of the ground and soil depth can be well fitted with a cubic polynomial.
loess area; subway station; shaking table test; dynamic soil pressure; horizontal displacement; settlement analysis
国家自然科学基金(41472267);中央高校基本科研业务费专项(310828171010);西安市地下铁道有限责任公司科研基金(D4-YJ-042014048)
2015-10-30 修改稿收到日期:2016-02-23
权登州 男,博士,讲师,1983年8月生
王毅红 女,博士,教授,博士生导师,1955年1月生
E-mail:wangyh@chd.edu.cn
P315.97
: A
10.13465/j.cnki.jvs.2017.17.018

