基于FAHP的电子对抗系统可靠性分配

张云鹏,陈立明

(电子工程学院,安徽 合肥 230037)

基于FAHP的电子对抗系统可靠性分配

张云鹏,陈立明

(电子工程学院,安徽 合肥 230037)

可靠性分配是系统设计的一个重要环节，电子对抗系统技术体制新、结构复杂，对大量分系统和组件单元实施可靠性分配的难度较大。通过构建电子对抗系统的可靠性模型，将可靠性分配问题转化为权重分配问题，并结合模糊层次分析法(FAHP)的流程和特点，提出了基于模糊层析分析法的系统可靠性分配方案。给出了实例运算和结果分析，验证了方法的可行性。

电子对抗系统;可靠性分配;模糊层析分析法;故障率

0 引 言

电子对抗装备在现代信息化战争中发挥着重要作用。在复杂的战场电磁环境中，电子对抗装备的可靠性决定其作战效能的发挥。因此，可靠性设计就是电子对抗系统的生命。可靠性分配是可靠性设计中的重要环节，它是将预计的可靠性指标值自上而下、由整体到局部地分配至各分系统、组件乃至元器件，以明确装备各系统和单元的可靠性设计要求。传统的可靠性分配方法包括等分配法、比例分配法和按重要度分配法等，这些方法一般适用于简单系统。电子对抗系统结构组成复杂，信号接收处理、系统管理和功率放大等多个模块对可靠度的需求差别较大，因此需要一种更精准、更科学的可靠性分配方法。

本文首先依据电子对抗系统的功能结构关系构建系统的可靠性模型，明确了系统各部分的层级关系和串联属性，将可靠性分配问题转化为权重分配问题。并结合模糊层次分析法的流程和优点，提出基于模糊层次分析法(FAHP)的可靠性分配方案。FAHP将模糊理论与层次分析法相结合，克服了层次分析法中判断一致性与人类思维一致性存在的显著差异，并且无需进行一致性检验，降低了权重分析的难度。最后通过实例运算，验证方案的可行性。

1 电子对抗系统的可靠性模型

可靠性分配是对可靠性指标进行由整体到局部的分解过程，对电子对抗系统进行可靠性分配，首先要明确系统各组成部分的结构关系和故障逻辑关系，构建系统可靠性模型，再依据可靠性模型对系统进行可靠性分配。

电子对抗系统结构相对复杂，要根据系统的功能要求及相互关系将系统的结构层次化。从功能来说，一般的电子对抗系统具有侦察、分析、干扰和通讯等功能[1-2]，结合某型装备可得电子对抗系统的典型构成如图1所示。

根据电子对抗系统的功能结构关系，可将所有组成单元实际划分为4个分系统：侦察分系统、干扰分系统、系统管理分系统和通信设备。同时将系统结构分为3层，最顶层M为电子对抗系统，中间层F为分系统成，最底层P即为分系统的组成单元。各单元之间信息交互频繁，相互依赖性较强，某一单元故障都将导致系统失常。对于最顶层电子对抗系统M，F1、F2、F3和F4任一分系统故障，系统均不能正常工作；对于侦察分系统F1，P1、P2和P3任一组件单元故障，F1均不能正常工作，故将P1、P2和P3故障作为F1故障的下层隶属关系。F2、F3和F4同理，可得系统的故障逻辑关系如图2所示。

依据对系统故障逻辑的分析，并假设该系统P及以上层级无其它冗余性设计，则可以构建电子对抗系统的串联型可靠性模型。该模型中各组成部分的层级关系同图2，且同层级各部分均满足串联属性。

电子系统在工作中的故障是随机的，其可靠度一般服从指数分布[3]，结合电子对抗系统的串联型可靠性模型，可得系统可靠度满足：

(1)

式中：Rs为系统的可靠度；λi、ti分别为第i个单元的故障率与工作时间。

假设各单元工作时间基本相同，则系统的可靠度表达式为：

Rs(t)=e-λsτ

(2)

(3)

系统可靠度仍服从指数分布，λs为系统的故障率。由式(3)可得系统各单元所分配到的故障率λi在系统总故障率λs中分别占有一定比重。当某单元相对于另一单元更为重要，替换和修复难度更大时，其分配的故障率应该更小；当某单元复杂程度高、工作环境更恶劣时，其分配的故障率应该更高。因而需要根据可靠性原则对系统各单元进行权重排序，获得各单元的权重值ωi。由于权重值与各单元分配的故障率成反比，单元i所分配的故障率为：

(4)

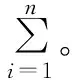
通过对电子对抗系统可靠性模型的分析，将可靠性分配问题转化为求解系统单元的权重排序问题，因此可以利用模糊层次分析法的思想对系统各单元权重进行定量分析，较为科学地获得权重向量W，实现各单元之间的量化比较和排序。

2 模糊层次分析法(FAHP)在可靠性分配中的应用

为了改进传统层次分析法中判断一致性与矩阵一致性相异、一致性检验困难与缺乏科学性等问题，一些学者提出了基于模糊一致矩阵[5]的模糊层次分析法。模糊层次分析法采用0.1～0.9标度[5-6]，一般流程包含构建优先关系矩阵、转化为模糊一致矩阵与获取权重向量。

结合模糊层次分析法的一般流程[6]对电子对抗系统各分单元进行权重排序，步骤如下：

(1) 首先通过系统中同一层级各单元的相互比较，利用数理统计或者经验数据构建优先关系矩阵A=(aij)n×n。其中，aij即为分单元i相对于分单元j的比较值。构建矩阵时采用0.1～0.9标度，其中0.5代表2个单元赋予的权重相同，0.5～0.9表示前者相对于后者权重依次增加，0.1～0.5则为反比较。

(2) FAHP的关键在于由优先关系矩阵A建立模糊一致矩阵R=(rij)n×n，模糊一致性矩阵满足一致性条件，无需再进行一致性检验[6-7]。

rij=(ri-rj)/2n+0.5

(5)

(6)

(3) 文献[7]～[8]中涉及到行和归一法、方根法和排序法[8]3种方法用来求解初权重向量，依次为：

(7)

(8)

(9)

(4) 为解决解的精度及收敛速度问题，文献[9]引用幂法来计算精度较高的且与实际情况较为吻合的排序向量。先将模糊一致矩阵R=(rij)n×n转化为互反判断矩阵E=(eij)n×n，其中，eij=rij/rji。将初权重向量W0作为初始向量，根据Wk+1=EYk，Yk=Wk/‖Wk‖max，k=1,2,…进行迭代，‖·‖max为向量中各元素模值的最大值。给定误差限度ε，当‖Wk+1‖max-‖Wk‖max<ε，即可结束迭代，并取最终的权重向量为:

(10)

再将最终求得的权重值代入式(4)求解各单元分配到的故障率。模糊层次分析法能有效处理多层级的权重分析问题，克服了层次分析法中判断一致性与人类思维一致性存在的显著差异，并且这里引用了幂法解决精度与收敛问题，利用迭代求得精度更高的权重向量。FAHP适用于结构复杂、技术较新的电子对抗系统，在实施中科学准确、可行性强。

3 实例运算

假定某电子对抗系统的预计可靠性指标为tMTBF=200 h，即总故障率为λs=1/tMTBF=5×10-3/h。通过第1节中对电子对抗系统可靠性模型的分析可知，系统按结构关系可分为O层、F层和P层3层，且F层中各分系统与P层中各组件单元均视为串联型结构，即上层与下层的故障率关系满足式(3)。先构建各分系统(F1～F4)的模糊一致矩阵，求解权重向量，将总故障率分配至各分系统。再以分系统所分配的故障率为基础，对各分系统下属的组件单元进行二次分配。因此共需要构建4个模糊一致矩阵：O～(F1,F2,F3,F4)、F1～(P1,P2,P3)、F2～(P4,P5,P6,P7)、F3～(P8,P9)。

3.1 构建模糊一致矩阵

如在构建图2的各分系统(F1～F4)的优先关系矩阵时，αij即为分系统Fi相对于分系统Fj的比较值，根据0.1～0.9标度进行赋值。当然，在任意两者进行比较时需要根据可靠性原则进行权衡，可靠性原则包括工作时间长短、复杂程度、重要程度、环境适应力、替换修复难度等。当前者比后者工作时间更长、复杂程度更高、环境适应力更差时，其分配故障率相对较高，赋值应小于0.5；当前者比后者技术更成熟、重要度更高、复杂程度低时，其故障率应相对较低，赋值应高于0.5。

根据优先关系矩阵和公式(5)、(6)计算模糊一致矩阵依次为：

3.2 解算权重向量与可靠性分配

此处采用行和归一法求解出各模糊一致矩阵相对应的初权重向量。将每个初权重向量作为初始向量，利用幂法进行多次迭代，以获得精度更高的排序向量。此处设置误差限度ε=0.000 1，当‖Wk+1‖max-‖Wk‖max时，迭代停止，依次得到最终的权重向量：

WR=(0.293 2,0.227 7,0.293 2,0.185 8)T

WR1=(0.415 7,0.306 9,0.277 4)T

WR2=(0.443 8,0.205 8,0.211 1,0.258 4)T

WR3=(0.55,0.45)T

WR为各分系统(F1～F4)相对于系统整体的权重向量，WR1、WR2和WR3分别为各组件单元P相对于各分系统(F1～F3)的权重向量。根据权重向量完成可靠性指标的分配，结果如表1、表2所示。各组件单元分配的平均故障间隔时间(MTBF)如图3所示。

表2 组件单元可靠性指标分配表

4 结束语

模糊层次分析法可充分适应系统的层次结构模型，实现对系统各要素、各层次之间关系的定量比较分析，通过与实际经验比较，其可靠性分配结果较好。针对复杂的电子对抗系统，FAHP有效地避开一致性检验，完成了对系统可靠性指标的分配，可实施性较强。在应用中应注意：

(1) 在具体实施中，还可在系统各层之间增添准则层，包括技术水平、复杂程度、重要程度、替换修复难度等判断要素，同样以FAHP构建一致矩阵解算，以更准确地完成同一层各单元间的相互比较。

(2) 虽然无需进行一致性检验，但不代表优先关系矩阵就可以随意给出，应当充分结合经验及相关专业知识。且电子对抗技术处在快速发展中，系统设计需要进行多次可靠性分配，才能保证分配结果科学有效。

[1] 宋宝贵,沈如松.武器系统工程[M].北京：国防工业出版社,2009.

[2] 唐永年.雷达对抗工程[M].北京：北京航空航天大学出版社,2012.

[3] 陈锋.某雷达系统可靠性设计方案[D].南京：南京理工大学,2013.

[4] 林敬茂,江思定.层次分析法在产品系统可靠性分析中的应用[J].浙江科技学院学报,2006,18(4):291-294.

[5] 姚敏,张森.模糊一致矩阵极其在决策分析中的应用[J].系统工程理论与实践,1998(5):78-81.

[6] 张吉军.模糊层次分析法(FAHP)[J].模糊系统与数学,2000,14(2):80-88.

[7] 姚敏,张森.模糊一致矩阵及其在软科学中的应用[J].系统工程,1997,15(2):54-57.

[8] 张吉军.模糊一致判断矩阵3种排序方法的比较研究[J].系统工程与电子技术,2003,25(11):1370-1372.

[9] 李永,胡向红,乔箭.改进的模糊层次分析法[J].西北大学学报(自然科学版),2005,35(1):11-12.

[10] 周曼,沈涛,周荣坤.模糊层次分析法在综合电子信息系统标准适用性分析中的应用[J].电子学报,2010,38(3):654-657.

ReliabilityAllocationofElectronicCountermeasuresSystemBasedonFAHP

ZHANG Yun-peng,CHEN Li-ming

(Electronic Engineering Institute,Hefei 230037,China)

Reliability allocation is an important link in system design.For the electronic countermeasure system,the technology system is new and the structure is complicated,so the reliability allocation to a great deal of sub-systems and component units is difficult.Through constructing the reliability model of electronic countermeasure system,the reliability allocation problem is translated into weight allocation problem.Combining with the flow and characteristics of fuzzy analytical hierarchy process(FAHP),this paper proposes a project of system reliability allocation based on FAHP,gives an example calculation and result analysis,and validates the feasibility of the proposed method.

electronic countermeasure system;reliability allocation;fuzzy analytical hierarchy process;failure rate

TN97

：A

：CN32-1413(2017)04-0032-05

10.16426/j.cnki.jcdzdk.2017.04.009

2016-11-18