Floyd算法在最优路径中应用

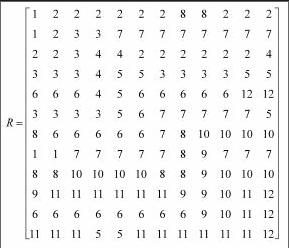
摘 要:采用Floyd算法作为求解该问题的核心算法,对时间邻接矩阵进行智能搜索,寻找到时间最少和路径最短的最优路径.及时确定最佳路线,以提高在实际问题应用效率.
YUAN Wei-Wei
(College of science, Heihe college, Heihe 164300, HeiLongJiang China)
Abstract To study the path of fire engines, to determine the best route to improve the fire speed, shorten the time the fire engine arrived at the fire. Use Floyd algorithm as the core algorithm to solve the problem of time adjacency matrix intelligent search, to find the shortest path and minimum time optimal path.
Key words: Floyd algorithm; Path optimization; Directed graph
求解最佳路径的过程即寻找最短时间和最短路径,我们将路径抽象为有向图,利用有向图的邻接矩阵。使用Floyd算法对时间邻接矩阵进行智能搜索,寻找到时间最少和路径最短的最优路径。
1 Floyd算法核心思想
Floyd算法又称为插点法,是一种用于寻找给定的加权图中顶点间最短路径的算法。通过一个图的权值矩阵求出任意两点间的最短路径矩阵。从图的带权邻接矩阵A=[aij]n×n 开始,递归地进行n次更新:由矩阵D=[0]=A ,按公式,构造出矩阵D=[1] ;又用同样地公式由D=[1] 构造出D=[2] ;……;最后又用同样的公式由D=[n-1] 构造出矩阵D=[n] 。矩阵D=[n] 的i行j列元素便是i号顶点到j号顶点的最短路径长度,称D=[n] 为图的距离矩阵。
图的邻接矩阵存储结构形式说明:
#define MaxVertexNum 50 //最大顶点数
typedef char VertexType; //顶点类型
typedef int EdgeType; //边上的权值类型
typedef struct{
VextexType vexs[MaxVertexNum] //顶点表
EdeType edges[MaxVertexNum][MaxVertexNum];//邻接矩阵,可看作边表
int n,e; //图中当前的顶点数和边数
}MGragh;
建立无向网络的算法
void CreateMGraph(MGraph *G)
{//建立无向网的邻接矩阵表示
int i,j,k,w;
scanf("%d%d",&G->n,&G->e); //输入顶点数和边数
for(i=0;i
G->vexs[i]=getchar();
for(i=0;i
for(j=0;j
G->edges[i][j]=0; //邻接矩阵初始化
for(k=0;k
scanf("%d%d%d",&i,&j,&w);//输入边(v i ,v j )上的权w
G->edges[i][j]=w;
G->edges[j][i]=w;
}
}//CreateMGraph
2 应用举例
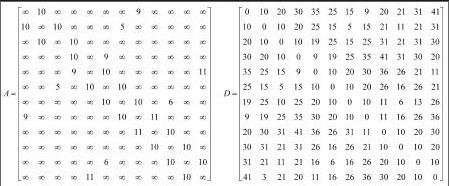
求解图一的最优路径,我们可以得到邻接矩阵A,通过matlab 软件程序,借助Floyd 算法可以轻松求出距离矩阵D
我们能够求出路径
3.结论
采用floy算法能够及时准确地获取动态的耗时特征,对时间邻接矩阵进行智能搜索,寻找到时间最少和路径最短的最优路徑做出准确合理的应急决策。适合复杂和多点图,可以通过程序重复使用,只需输入相应的仞始数据即可,极大的提高在实际问题应用效率.
参考文献:
[1] 李蔚萱.图论[M].长沙:湖南科学技术出版社,1980.91-11.5
[2] 李刚.离散数学[M].上海,复旦大学出版社,2006:225-230. [3] 耿素云,屈婉玲.离散数学[M].北京:北京大学出版社,2002.
作者简介:袁威威,( 1982—),女,黑龙江黑河市人,黑河学院理学院数学系讲师,从事数学与应用数学
基金项目:黑河学院科学技术研究项目《基于黑河中俄自由贸易园区背景下消防布控最优化问题的研究》,项目编号:KJQ201601

