基于方向梯度的WSN三维覆盖策略

王丹丹 徐汀荣

(苏州大学计算机科学与技术学院 江苏 苏州 215006)

基于方向梯度的WSN三维覆盖策略

王丹丹 徐汀荣

(苏州大学计算机科学与技术学院 江苏 苏州 215006)

针对无线传感器网络中的三维表面覆盖问题，提出一种基于方向梯度的覆盖算法。首先将三维表面垂直投影到二维平面上，然后采用区域离散化的思想，将二维平面离散成若干个网格点，再根据方向梯度概率感知模型，确定每个点覆盖的范围，最后通过贪婪算法找出满足覆盖率的最小覆盖集。该方法采用的方向梯度概率感知模型，充分考虑了三维表面地形的影响以及实际应用中的感知范围衰减因素。通过大量仿真实验表明，该方法能有效覆盖三维区域。

无线传感器网络 三维表面覆盖 方向梯度

0 引 言

近年来，无线传感器网络WSN在军事、工农业控制、城市管理、抢险救灾等各个领域得到了广泛应用。无线传感器网络通过部署在监测区域中的传感器节点进行数据收集，然后把数据发送给汇聚节点，汇聚节点再通过互联网或卫星传输给任务管理节点。在无线传感器网络中，节点的部署是基本且重要的问题。

最早对无线传感器网络覆盖问题的研究主要集中在二维理想平面，节点采用传统的圆盘模型对目标监测区域进行覆盖。随着对无线传感器网络技术研究的不断深入，二维平面模型越来越不适用于现实世界中的复杂应用场景，基于空间的三维无线传感器网络成为无线传感器网络研究中的热门领域，与二维平面中节点的圆盘感知模型不同，三维空间中的节点模型为球体感知模型。三维表面覆盖是三维无线传感器网络中的一种特殊情形，对应于现实世界中的山体，是在实际应用场景中衍生出来的一种新的网络模型。文献[1]针对三维表面覆盖问题，先把目标区域分成N个子区域，再利用多目标覆盖的遗传算法在各个子区域中进行选择、交叉、变异操作，来保证网络的覆盖和连通。该方法基于圆盘感知模型，没有考虑地形对其感知范围的影响。文献[ 2 ]选用马鞍形曲面进行研究，节点的感知模型选用符合三维曲面固有特性的概率感知模型。先随机部署传感器节点，再利用差分进化算法进行优化，实现对目标区域中节点部署问题的研究。该方法是在规则三维表面进行的节点部署，不能满足实际应用需求。文献[ 3 ]提出了一种把降维和遗传算法相结合来解决三维覆盖问题的策略。针对无线传感器网络中的确定性覆盖问题,首先把三维曲面进行降维,然后采用改进的遗传算法通过不断迭代来搜索全局最优覆盖解。文献[ 4 ]把三维表面覆盖问题分为规则地形覆盖和不规则地形覆盖两类。规则地形提出圆锥模型和余弦模型来刻画，从而得出期望覆盖率。针对不规则地形，采用基于数字高程模型中的规则三角网解决方案，来估算网络的期望覆盖率。文献[ 5 ]中使用基于方向梯度的感知模型对已经部署好节点的三维表面进行陷阱空洞的检测。使用该模型与之前的圆盘模型相比，原有陷阱空洞的直径增加，并且能发现新的陷阱空洞，该模型更能反映起伏地形的特征。

本文基于方向梯度感知模型提出了一种对传感器节点进行确定性部署的方法。充分考虑三维表面地形对节点感知范围的影响，根据节点在各个方向上的方向梯度大小，确定每个点的实际覆盖范围。由于方向梯度的感知模型是非线性模型，求解感知范围比较困难，因此通过区域离散化的方法，把求解覆盖范围转化为求解覆盖点。考虑到信号衰减等因素的影响，利用概率感知模型，确定节点对每个点的感知概率，再利用贪婪算法找出满足目标覆盖率的最小覆盖集。

1 覆盖策略描述

1.1 网络模型

本文在三维区域中根据提出的算法确定性部署若干个节点，采用如下假设：

a) 传感器节点沿各个方向的理想探测半径为r。

b) 不考虑三维表面凹凸点对感知结果的影响。

1.2 基于方向梯度的覆盖算法

考虑三维表面的影响，采用基于方向梯度的感知模型对目标区域进行覆盖。

1.2.1 三维转化成二维

由于节点的感知模型是球体，而三维表面是不规则的，无法确定节点在三维上的感知区域，从而在三维表面直接确定节点的覆盖集是比较困难的，所以本文采用投影的方式，把三维表面垂直投影到二维上，在二维上进行覆盖集的选取。

1.2.2 基于方向梯度的概率感知模型

把三维问题转化为二维问题后，若直接采用二维上的圆盘感知模型会造成如图1所示的问题[6]。在二维平面上可以完全覆盖，在三维上却会出现覆盖漏洞。所以本文把基于方向梯度的感知模型[5]和指数衰减概率模型[7]相结合得到了基于方向梯度的概率感知模型。

图1 三维感知漏洞问题

用坡度表示地形陡缓程度，如图2所示，把坡面的垂直高度h和水平距离l的比叫作坡度，用字母i表示。坡向是斜坡面对的方向，即高度下降最快的方向。

(1)

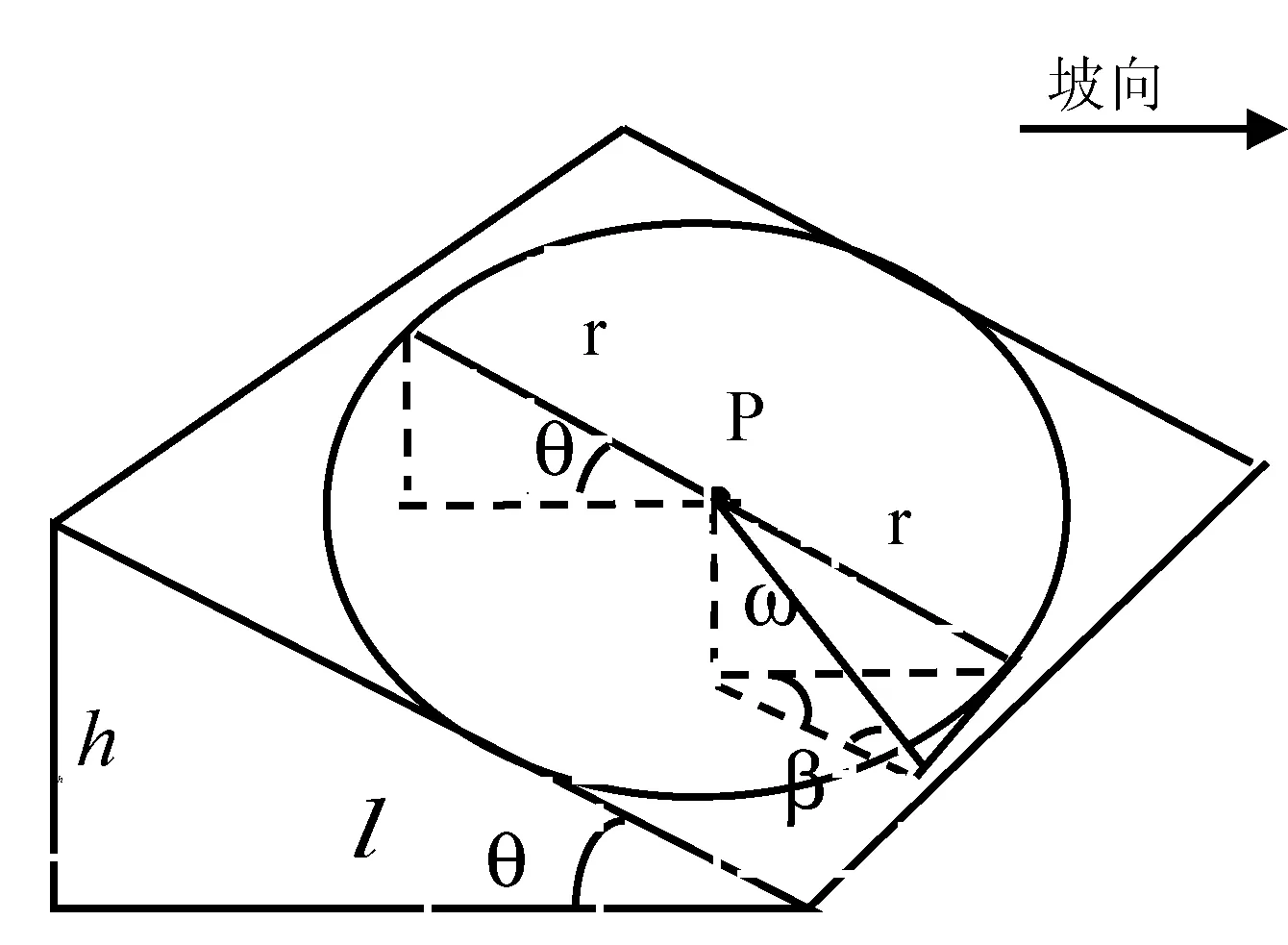
图2 坡度和方向梯度概念

为了表示坡面上的点沿任一方向高程值的变化，引出了方向梯度的概念，用g表示。

(2)

其中，ω表示方向角，即与坡向的夹角。当ω为0时，即方向与坡向一致，此时方向梯度等于坡度。

由式(1)、式(2)两个公式可以推出该点沿ω方向的实际感知半径，用sr表示。

sr=rcos[arctan(icosω)]

(3)

由此可得出坡面上任意一个点的覆盖区域。

因为在实际三维应用场景中，监测结果受到噪声干扰，信号衰减等因素的影响，所以需要采用如下所示的概率感知模型来反应节点的实际监测能力，P(s,t)表示节点s监测到目标点t的概率。

(4)

其中，d=d(s,t)-(sr-ur)，d(s,t)表示节点和目标点的距离，α和β是衰减因子。sr是利用方向梯度感知模型预先计算好的节点感知半径，ur是一个不确定的感知范围，当目标点t在sr-ur范围内的时候，能百分百被覆盖，当目标点在sr+ur范围外的时候，不能被覆盖，当目标点介于两者之间时，感知概率满足式(4)中的指数函数。

1.2.3 区域离散化

由于方向梯度感知模型得到的覆盖半径是可变的，求解相应面积时比较复杂，所以本文采用区域离散化的方法，把平面区域上的覆盖转化成点的覆盖问题。如图3所示，椭圆所在区域是点的覆盖区域，把其中包含的完整网格离散化形成图4所示区域中的点，根据文献[ 8 ]中的引理，该方法能保证所求离散问题的可行解也是对原来对应连续问题的可行解。

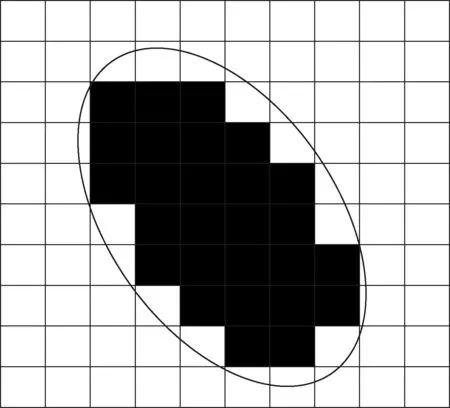
图3 节点覆盖区域

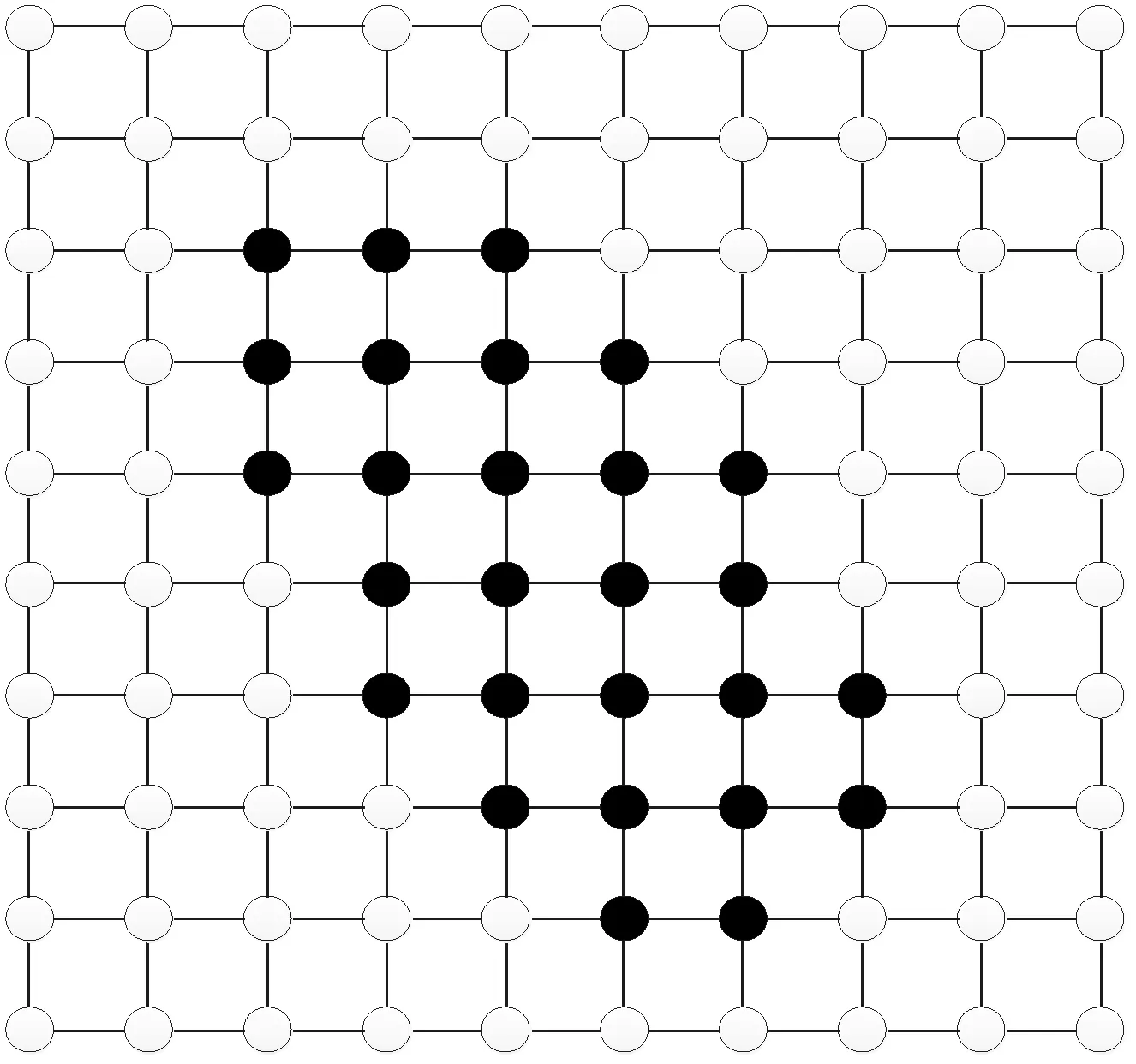
图4 离散化后需要覆盖的点集

1.2.4 贪婪算法

把离散化后形成的网格点的位置作为覆盖集节点的候选位置。节点覆盖的最终目标是覆盖网格点的概率尽可能大。经过区域离散化后可以确定每个节点覆盖的网格点的概率，依次遍历每个节点，从中选取使得现有覆盖概率提升最大的点加入覆盖集，每次选取完之后，加入覆盖集的节点不参加下一轮的选举，在剩下的点中选取覆盖概率提升最大的点加入。重复进行上述步骤直到区域中每个网格点被覆盖的概率达到95%以上，由此确定覆盖集。完整的覆盖集生成算法如下：

算法1基于方向梯度概率模型的贪婪算法

输入：划分网格大小rows×cols，三维表面网格顶点坐标w(x,y,z)，感知半径sr，不确定感知范围ur。

输出：覆盖集C，每个点的平均覆盖概率P。

标记：currP:记录每个点当前覆盖概率的数组G:网格点集

第1步C=∅

第2步

1) 划分网格，记录每个网格中心点的位置坐标，把该网格点g加入G

从表2中的数据可看出，用GM(1，1)模型得到的预测值并不是很理想，其平均相对误差为0.038 2%。利用GM(1，1)预测模型来预测第8次沉降值，得到的预测沉降值为20.76，相对误差为0.055%，后验差比值C为0.065。

2) 根据每个网格点的高度信息，得出每个点的坡度，坡向，存储到坡度矩阵SlopeMatrix，坡向矩阵AspectMatrix中

第3步 根据上述坡度坡向信息，结合概率感知模型，确定每个点对其他点的感知概率

第4步 While(P<0.95)

a) 对每个点g∈G,计算点g加入C后，currP提高的概率

b) 找出能使currP提升最高的点v，C=C∪{v}

c) 更新currP中目前对每个点的覆盖概率

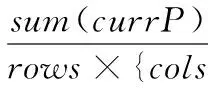
第5步 ReturnC,P

2 算法分析

在第二阶段根据坡度矩阵和坡向矩阵信息，确定每个点对其他点的覆盖概率，需要使用两重循环遍历查找所有点，对应的时间复杂度为O(n2)，把找出来的结果存储到一个矩阵中，第i行存储编号为i的点对其他点的覆盖概率。

在第三阶段，循环选取网格点加入覆盖集，直到覆盖概率达到目标覆盖阈值。每次循环需要遍历所有未加入覆盖集的网格点，找出使覆盖概率提高最多的点加入覆盖集，之后更新当前所有点的覆盖概率，该过程的时间复杂度为O(n2)。循环的执行次数要根据实际选取的节点感知半径还有网格大小决定，最坏情况总的时间复杂度为O(n3)。

3 实验仿真与结果分析

实验采用MATLAB进行仿真，在如图5所示的三维表面进行节点的部署。

图5 三维表面

3.1 实验仿真参数设置

实验过程中的参数值设置如表1所示。二维平面大小指图5所示的三维表面垂直投影到平面上形成的区域大小。

3.2 仿真结果及分析

图6是把二维平面划分成50×50个网格，利用本文提出的覆盖策略进行实验得出的节点部署位置。该图是节点投影到二维平面上形成的图，图中节点分布比较密集的部分是山体区域，该区域坡度比较大，映射到平面后，相应的覆盖半径比较小，因而部署密集。而在平原地区，节点的部署比较稀疏。

图6 覆盖集节点分布图

下面考虑网格划分大小对覆盖集大小的影响，如图7所示。

图7 覆盖集和网格点关系图

图7中横坐标表示划分成的网格的粒度，例如，50表示划分成50×50个网格，纵坐标表示覆盖集的大小。随着网格数的增加，覆盖集的大小基本在97个左右波动。网格划分得越细越能表现三维的地形特征，从而得出的覆盖集更具有实际意义。

4 结 语

为了解决三维表面上的确定性部署问题，本文提出基于方向梯度的覆盖算法进行求解。目前，关于二维平面和三维空间上的覆盖问题的研究很多，但是基于三维表面的研究很少。本文提出的基于方向梯度的覆盖算法为该类问题提供了一种可行性方案，利用区域离散化方法近似表示目标区域，再用贪婪算法求出了三维表面的覆盖集，并通过仿真实验验证了该方法在三维表面环境中是正确并且可靠的。

[1] Unaldi N,Temel S.Wireless Sensor Deployment Method on 3D Environments to Maximize Quality of Coverage and Quality of Network Connectivity[C]//World Congress on Engineering and Computer Science,2014.

[2] 陈树,季忠军.复杂三维曲面覆盖算法研究[J].计算机工程与应用,2016,52(20):127-131.

[3] Feng L,Sun Z,Qiu T.Genetic Algorithm-Based 3D Coverage Research in Wireless Sensor Networks[C]//Seventh International Conference on Complex,Intelligent,and Software Intensive Systems.IEEE,2013:623-628.

[4] Liu L,Ma H.On Coverage of Wireless Sensor Networks for Rolling Terrains[J].IEEE Transactions on Parallel & Distributed Systems,2012,23(1):118-125.

[5] 刘晔,傅忠谦.基于地形修正的无线传感器网络陷阱空洞检测[J].传感技术学报,2014(6):785-790.

[6] Zhao M C,Lei J,Wu M Y,et al.Surface coverage in wireless sensor networks[J].Proceedings-IEEE INFOCOM,2009,39(3):109-117.

[7] Zou Y,Chakrabarty K.Sensor deployment and target localization based on virtual forces[C]//Joint Conference of the IEEE Computer and Communications.IEEE Societies.IEEE,2003,2:1293-1303.

[8] 赵铭辰.无线传感器网络表面覆盖问题的研究[D].上海交通大学,2010.

AMETHODOFCOVERAGEINTHREE-DIMENSIONALWSNBASEDONDIRECTIONALGRADIENT

Wang Dandan Xu Tingrong

(SchoolofComputerScienceandTechnology,SoochowUniversity,Suzhou215006,Jiangsu,China)

Aiming at the problem of 3D surface coverage in wireless sensor networks, a coverage algorithm based on directional gradient is proposed. First, the 3D surface was projected onto the 2D plane directly by the projection method. Then, the 2D plane was divided into a number of grids and each grid was considered as a grid point by the way of zone discretization. Next the actual sensing radius of each direction was decided by the directional gradient probability sensing model. Finally, we found the minimal cover set satisfying the coverage rate using the greedy algorithm. In this method, the directional gradient probability sensing model was adopted, which fully considered the influence of the 3D surface topography and the attenuation factor of the sensing range in the practical application. A large number of simulation experiments show that the proposed algorithm can effectively cover the 3D terrains.

WSN 3D Coverage Directional gradient

TP393

A

10.3969/j.issn.1000-386x.2017.09.028

2016-11-06。国家自然科学基金项目(61472469)。王丹丹，硕士生，主研领域：无线传感器网络。徐汀荣，教授。