基于改进坡度的自适应数学形态学点云滤波

陈斐然，李 浩，李语旻，陈仁喜

（1.河海大学 地球科学与工程学院，江苏 南京 210098）

基于改进坡度的自适应数学形态学点云滤波

陈斐然1，李 浩1，李语旻1，陈仁喜1

（1.河海大学 地球科学与工程学院，江苏 南京 210098）

首先介绍了传统形态学算法，并分析了其应用方面的不足；然后提出了一种基于改进坡度参数的自适应形态学滤波方法；最后利用实际点云数据进行了实验。该方法通过划分格网自动计算当前区域坡度的平均值，从而得到适当的坡度参数用于后续高度阈值的计算。实验结果表明，该方法能更有效地识别地面点和地物点，对被建筑物包围的植被点滤除效果明显。

LiDAR点云；数学形态学；滤波；分类

LiDAR不仅能快速获取大面积点云数据，而且能从中得到高精确DEM，因此受到各测绘行业的高度重视。点云滤波是LiDAR数据处理的重要内容之一，也是最先需要解决的问题。滤波分类精度的高低直接影响点云数据的使用质量。点云滤波即对在地形表面随机分布的离散点进行识别与处理，区分落在地面上的点（地面点）和落在地面物体上的点（植被﹑建筑物﹑车辆等地物点），分别形成地面点与地物点数据集合。

目前国内外已有许多专家学者对点云滤波方法进行了详细研究[1-2]。张子林[3]等使用基于TIN的滤波算法对高程突变地物进行了滤波，但对低矮的地面物体进行滤波时，误差会显著增大。参考文献[4]～[6]提出一种基于坡度变化的滤波算法，但该算法需提前知道地形坡度值，并确定窗口大小，区域内每个点都需进行坡度计算，并同其他点进行比较，以确定该点是否为地面点。同时，如果仅根据坡度设置统一的阈值，则会滤除掉一些真实的地形细节特征，造成分类误差，所以必须根据作业区域的实际地形状况设置不同的过滤参数值。另外一种常用的滤波算法是基于数学形态学原理的滤波算法[7-11]。数学形态学算法不仅可用于点云数据滤波，也可用于建筑物或道路点云数据的提取。然而现有的基于经典数学形态学算法的LiDAR点云滤波方法存在以下不足：①无法根据地形特点动态调整窗口。利用一个固定窗口大小的结构元素很难过滤各种尺寸的地物点，若窗口过小则只有较小的地物点被去除，如汽车或植被，但此时窗口无法完全包住大型建筑物，使得大型建筑物不能被有效滤除；而较大的滤波窗口对于含有山坡和低矮山包的地区而言，很容易将山包和山坡当成非地面点而错误滤除。②无法顾及窗口内地形的细节特征。使用一个固定的“高度阈值”作为判断是否为地面点的唯一标准显然是不合理的。③坡度参数没有考虑实际地形情况。坡度参数的取值由用户自己输入，并没有真正考虑地形起伏的实际情况，对后期滤波的准确程度产生影响。

本文对传统数学形态学滤波算法进行了改进，提出了一种基于改进坡度参数的自适应数学形态学滤波算法，不仅能自动调整窗口大小，而且可以通过划分格网来自动计算当前区域坡度的平均值，得到适当的坡度参数用于后续高度阈值的计算，使得对LiDAR点云的识别更加准确。

1 数学形态学滤波方法

1.1 经典数学形态学滤波

数学形态学是基于集合运算原理进行特征提取的，其中集合表示图像中不同的对象。腐蚀与膨胀分别用于减少或增大图像中特征形状的尺寸。腐蚀运算即以窗口内高程的最小值代替窗口中心的高程值，而膨胀运算即以窗口内高程的最大值代替窗口中心的高程值。

在采用数学形态学方法对LiDAR点云进行滤波时，一般使用这两个基础算子的组合，主要是开运算和闭运算，其表达式为：

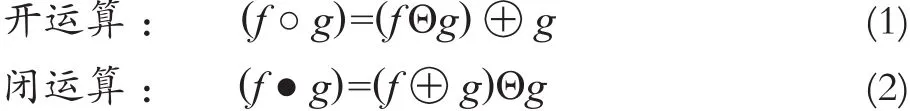
式中，Θ为腐蚀运算符号；⊕为膨胀运算符号；○为开运算符号；●为闭运算符号。

开运算是先腐蚀后膨胀的运算过程，可先将比结构尺寸小的地物点去除，再膨胀恢复被腐蚀的建筑物边缘形状。这种去除比结构元素窗口尺寸小的物体同时保留比结构元素窗口大的物体特性，常被用于提取LiDAR点云数据的地面点，因此在LiDAR点云滤波中得到广泛应用。

1.2 渐进式数学形态学滤波

针对单一窗口和单一阈值数学形态学滤波方法存在的问题，ZHANG K[7]等提出的渐进式数学形态学滤波方法可从LiDAR点云中滤除大部分的地物点（见图1）。

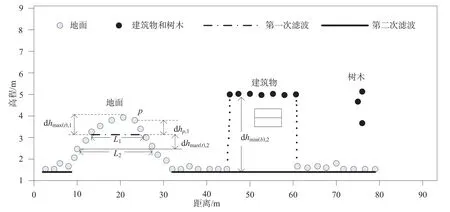
图1 渐进式数学形态学滤波方法

由图1可知，在第一次滤波处理后，比窗口尺寸L1小的树木点会被滤除，而大型建筑物则被保留；同样尺寸小于L1的地面特征被削平，山坡最高点的高程与第一次滤波后的高程差值为dhmax(t),1，而山坡上随机点P的高程与第一滤波后的高程差值为dhp,1。在随后的迭代过程中，窗口大小增加到L2，此时大型建筑物尺寸小于当前窗口尺寸，大型建筑物点被滤除，而地形特征点前后两次滤波的高程差值为dhmax(t),2。

引入坡度参数和高度阈值可避免滤波后起伏地形的高点被滤除，但无法保留地形的细节特征，将地形坡度参数s和每次迭代高程差阈值dhT,k分别定义为：

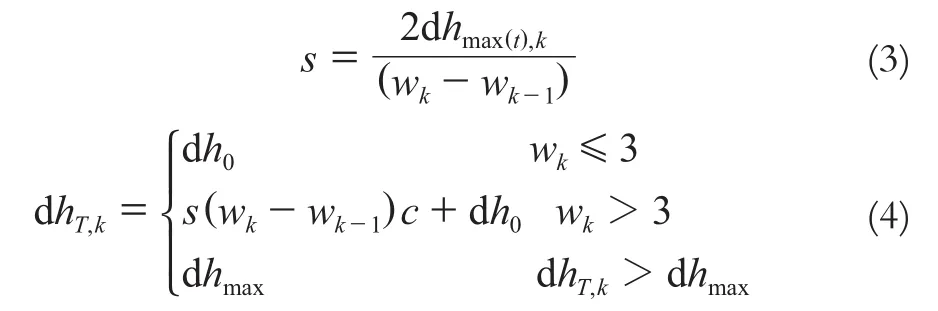
式中，dhmax(t),k为第k次滤波后与前一次滤波的最大高程差；wk为第k次滤波的窗口大小；c为格网间距；dh0为初始高差阈值；dhmax为最大高差阈值。如果某个点前后两次滤波的高程差值小于阈值，则分类成地面点，否则为地物点。

对于城市区域的LiDAR数据而言，若dhT,k取值适当，则可确保比s小的地形特征表面被保留下来。城市中主要的非地面点对象为建筑物﹑汽车﹑植被等，通过逐渐增大的滤波窗口重复使用开运算，汽车与植被点在首次运算时就会被滤除，而高大的房屋会在最后几次运算中被过滤掉。一般情况下，将最低房屋的高度设为最大高差阈值dhmax，以保证复杂建筑物被完全识别滤除。

2 自适应数学形态学滤波方法

[7]中，s的取值是由用户根据地形实际情况自己输入的，城市与山区地形的s取值有较大差别，且城市内部中的s也是不同的。本文采用首先规则划分格网并进行高程赋值，然后利用坡度公式求解当前区域各格网的坡度值，最终取其平均值作为区域近似坡度值的改进坡度参数形态学滤波方法，以提高算法在不同地形环境下的自适应能力和完善性。改进算法流程如图2所示。

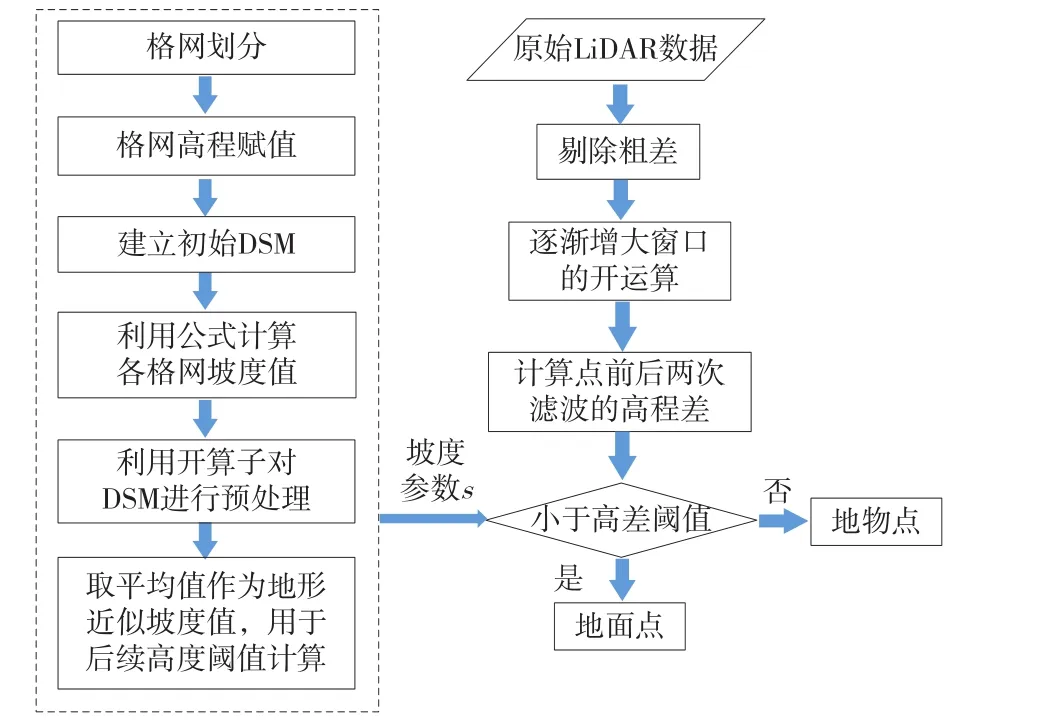
图2 改进算法流程图

格网尺寸过大会降低LiDAR点云高程的精度，而网格尺寸过小则会造成数据计算量过大﹑运行缓慢。将区域总面积除以区域内点云总数得到的平均点间距作为规则化点云格网的大小c，这样做的目的是使得大部分格网中只包含1个LiDAR点，满足一个激光点对应一个格网的要求。在此基础上，由已知区域内最大和最小的x﹑y值与某一个格网中激光点坐标计算得到该格网的行列号，并依次遍历全部点云数据。

格网规则划分完成后，则需对每个格网进行高程赋值。这里分为两种情况，一种是当有多个点落在同一个格网中时，则取其中最低点的高程作为该格网的高程；另一种是当格网中没有任何激光点时，则将最邻近点的高程值赋给该格网。所有格网赋值完成后，再利用新生成的规则格网高程数据建立初始LiDAR点云的数字表面模型（DSM）用于下一步坡度计算。

对于初始DSM，为了自动计算地表面的坡度值，本文使用二阶坡度计算公式来计算每个格网所对应的坡度值：

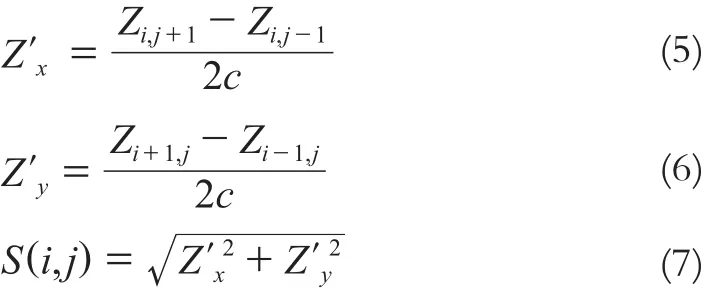
式中，Zi,j+1﹑Zi,j-1﹑Zi+1,j﹑Zi-1,j分别对应相应格网行列号的格网高程值；c为格网大小。

将式（5）﹑（6）代入式（7）中就可计算得到各格网的坡度S(i, j)，但该坡度并不是所需要的实际地形坡度，而是地表坡度。在得到的地表坡度中，除了一小部分地面坡度外，其余绝大多数是植被﹑建筑物等地物点产生的坡度。为了能获得实际地形的近似坡度值，必须进行预处理。本文首先利用合适窗口大小的开算子遍历全部地表坡度值，以剔除建筑物和部分植被对坡度的影响。由于坡度平均值代表区域内地形的普遍情形，为了进一步消除建筑物周围植被对坡度的干扰，再对当前区域的全部格网坡度值进行相应运算，取其平均值作为该区域的近似坡度，并用于后续高度阈值的计算，最大限度地保留实验区域的地形细节特征。

3 实验结果与分析

3.1 实验数据与结果

实验数据采用ISPRS网站提供的城市点云数据，主要是由大小不一的建筑物及不同高度的植被所组成。实验区域大小为1 450 m×505 m，点云高差为50 m，点云间距为1.5 m。原始点云如图3所示，可以看出实验区分布着大﹑中﹑小不规则形状的建筑物，同时有道路﹑汽车﹑树木等地物。图4为采用基于改进坡度参数的自适应数字形态学滤波方法滤波后的结果。

在原始点云中选取一处复杂城市环境作为样本，共有26 984个离散激光点，图5b为采用渐进式数学形态学滤波算法的结果，图5c为采用本文算法的结果。

图3 原始数据

图4 改进算法滤波结果

图5 复杂区域滤波结果

3.2 实验结果分析

实验结果表明，基于改进坡度参数的数学形态学滤波方法能更有效地区分地面点与地物点。在图4中，绝大多数植被与建筑物都被滤除掉，同时大部分地面细节特征得以保留下来。从图5b可以看出，渐进式数学形态学滤波对被建筑物包围的植被点滤除效果不佳，而本文提出的改进算法能有效去除建筑物周围的植被点，保留地面真实信息。

为了能更好地定量分析实验结果，将样本区域的人工判读分类结果作为准确分类结果（地面点14 023 个，非地面点12 961个），统计参考文献[7]的算法和本文提出的改进算法的误差。第Ⅰ类误差﹑第Ⅱ类误差和总误差的定义如表1所示。表2为在样本区域滤波结果中两种算法的误差对比。

表1 滤波误差的定义

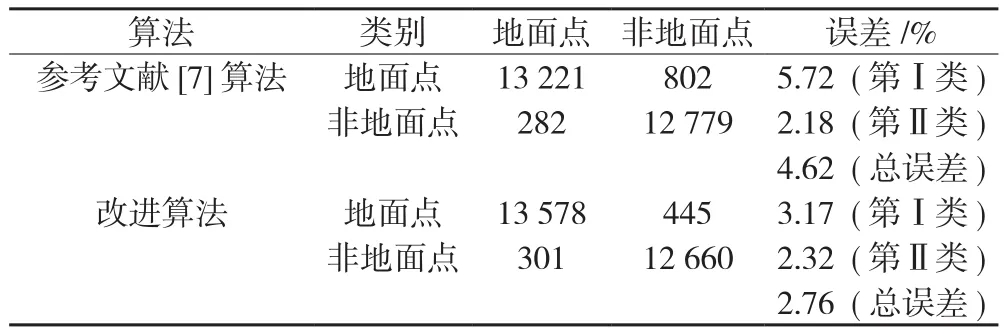
表2 滤波结果定量分析

从表2可以看出，改进算法的第Ⅰ类误差较参考文献[7]算法有明显降低，说明地面点识别分类更加精确；而第Ⅱ类误差没有太大的变化，总误差则明显低于参考文献[7]算法。

4 结 语

本文所提出的基于改进坡度参数的自适应数学形态学滤波方法对现有的数学形态学滤波算法进行了改进，采用了自动划分格网求解坡度平均值作为坡度参数，并用于后续高度阈值计算的方法，有效解决了被建筑物包围的植被点滤除问题。实验结果显示，该方法能有效区分地面点与非地面点，并进一步保留了地形的细节特征，降低了滤波误差。

参考文献

[1] 王金亮,陈联君.激光雷达点云数据的滤波算法述评[J].遥感技术与应用,2010,25(5):632-638

[2] ZHANG K, Whitman D. Comparison of Three Algorithms for Filtering Airbone LiDAR Data[J].Photogrammetric Engineering & Remote Sensing,2005,71(3):313-324

[3] 张子林,门林杰.基于TIN改进的LiDAR滤波算法 [J].工程地球物理学报,2012,9(3):362-364

[4] 许可,王运巧,胡少兴.基于坡度与迭代运算的LiDAR点云数据滤波[J].机械工程与自动化,2016(2):71-73

[5] 张宁宁,杨英宝,于双.基于坡度和区域生长的城市LiDAR点云滤波方法[J].地理空间信息,2016,14(3):30-32

[6] Sithole G. Filtering of Laser Altimetry Data Using a Slope Adaptive Filter[J]. International Archives of Photogrammetry and Remote Sensing,2001,34(3/W4):22-24

[7] ZHANG K,CHEN S C, Whitman D, et al. A Progressive Morphological Filter for Removing Nonground Measurement from LiDAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing,2003,41(4):872-882

[8] 隋立春,张熠斌,柳艳,等.基于改进的数学形态学算法的LiDAR点云数据滤波[J].测绘学报,2010,39(4):390-396

[9] CHEN Q, GONG P , Baldocchi D ,et al. Filtering Airborne Laser Scanning Data with Morphological Methods[J].Photogrammetry Engineering and Remote Sensing,2007,73(2):175-185

[10] 罗伊萍,姜挺,龚志辉,等.基于自适应和多尺度数学形态学的点云数据滤波方法[J].测绘科学技术学报,2009,26(6):426-429

[11] 李峰,崔希民,袁德宝,等.改进坡度的LiDAR点云形态学滤波算法[J].大地测量与地球动力学,2012,32(5):128-132

P228

B

1672-4623（2017）09-0028-04

10.3969/j.issn.1672-4623.2017.09.010

2016-09-18。

项目来源：国家自然科学基金资助项目（41471276）。

陈斐然，硕士研究生，研究方向为LiDAR数据处理与地图制图。