基于集中质量法的水下拖曳缆索动力响应分析
刘 铭,李家旺,朱克强
(宁波大学 海运学院,宁波 315211)
基于集中质量法的水下拖曳缆索动力响应分析
刘 铭,李家旺,朱克强
(宁波大学 海运学院,宁波 315211)
以水下拖曳缆索系统为研究对象,建立拖曳缆索的集中质量模型,推导了水下拖曳缆索的动力学方程。采用四阶Runge-Kutta数值积分算法,对水下缆索进行非线性动力响应分析。编制了相应的计算机程序,模拟拖曳缆索系统在匀速直航、横向运动、升沉运动、回转运动条件下,缆索的运动姿态及受力情况。数值分析结果与实验对比表明,集中质量模型对缆索在各种边界条件下的运动激励均有较好的适应性。相比基于有限差分法的数值结果,集中质量模型与实验结果吻合更好。
集中质量法;水下拖曳缆索;动力响应
在水下探测、无人深潜器、锚链悬挂等工程领域中,拖曳缆索具有较大的研究价值。1973年 Choo和Casarella对缆索系统运动分析方法进行了探讨,并描述了缆索系统运动仿真的多种模拟方法[1],1977年Russell[2]对拖点圆周运动的三维模型进行模拟[2],但无法模拟其他的运动形式。1980年Rispin[3]对拖曳缆索直航和圆周运动做了一系列的海上实验。1983年Ablow[3]对Rispin的实验模型中直航和圆周运动的缆索进行了基于有限差分法的数值模拟,研究了拖船作任意运动时水下拖曳缆索的位型,但是由于差分格式的选取原因,某些运动形式下数值解与实验结果相差较大。1986年Kennedy[4]对拖曳缆索在水平正弦运动下的运动响应进行了数值模拟和海上实验。1989年李立波[5]对拖曳阵系统进行了有限差分法的数值模拟,在Ablow基础上对差分格式进行了优化。2002~2014年朱克强等[6-7]先后模拟了多种缆体系统,以及采用凝集质量法对海洋缆索的回转运动进行了数值分析,并推导了一种凝集参数法表达式,但是并没有考虑缆索弯曲刚度的影响。2015年王志博等[8]基于有限单元法对拖曳系统的扰动特性进行研究,计算了二段式拖曳方式对扰动的传递特性。
为更全面地考虑水下缆索的受力,以及尽可能提高对多段式缆索的适应性,本文的研究计及缆索的弯曲刚度,并以某三段式拖曳缆索作为验算模型进行缆索动力分析。基于集中质量法,列出了缆索系统的动力学方程。集中质量法的优点在于算法简便、对边界条件的适应能力强。本文验算了拖船在多种运动状态(匀速直航、横向正弦运动、升沉运动、回转运动)下,三段式拖曳缆索系统的动力响应。通过多方面的计算以及与实验的比较,证明了本文的数值计算是比较有效的,不仅计算精度较高,且对拖曳环境下各种复杂运动具有较高的适用性。
1 缆索单元的动力学微分方程
拖船锚链、拖曳声纳、悬挂的海洋立管均可视为海洋缆索系统,海洋缆索主要受到水流阻力和拖船运动载荷的影响,在缆索的动力响应过程中,其惯性力、水流阻力、轴向张力以及弯矩随时间变化而变化,因此缆索动力学问题是典型的非线性问题。由于缆索动力学问题很难得到解析解,采用数值模拟是目前理论界与工程界的主流做法。
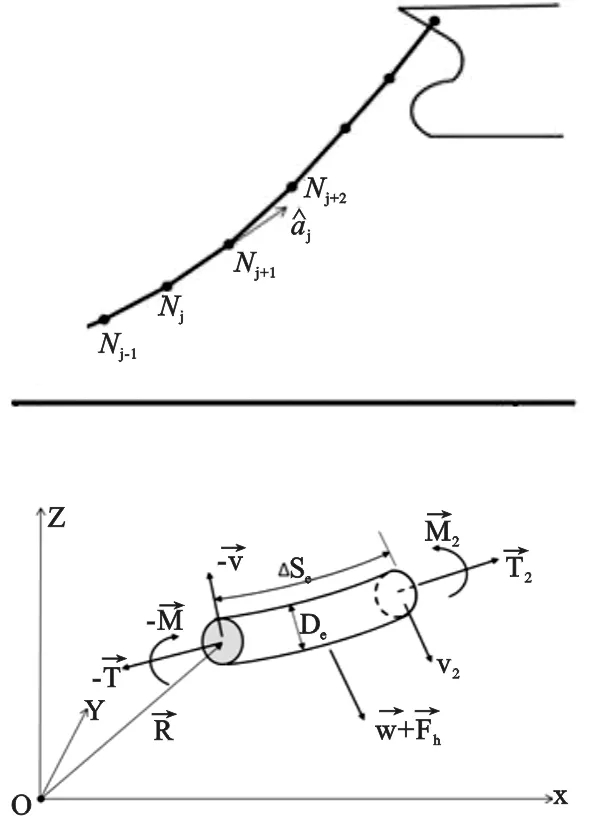
图1 缆索单元与受力Fig.1 Cable element and force
将缆索沿着长度方向划分为多个单元,如图1所示。选取一个缆索单元作为研究对象,则缆索单元的运动方程为
(1)
(2)

缆索的弯矩和张力分别与其弯曲刚度EI和拉伸刚度EA有关,用公式可表示为
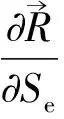
(3)
T=EAε
(4)
式中:ε为轴向应变。
为了确定式(1)和式(2)的唯一解,需建立缆索顶部与末端的边界条件方程
(5)
(6)
M(0)=M(L)=0
(7)

对于考虑弯曲的缆索,需要建立离散的集中质量模型,如图1所示。缆索被划分为若干个单元,每个单元的质量分配到单元两端的节点上。
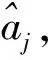
(8)
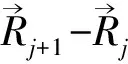
节点j处的曲率矢量可通过相邻缆索单元之间斜率变化率来表示
(9)
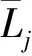
假设两个相邻单元之间的抗弯刚度EI恒定,那么式(3)又可表示为
(10)
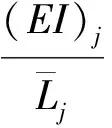
缆索单元的轴向和法向张量,分别为
(11)
(12)
如果分布弯矩为0,那么通过式(1)、(2)以及式(11)、(12)推导出单元j剪力的矩阵形式为
(13)
那么单元j两端节点的运动方程可表示为矩阵形式
(14)
式中:[Vj]=[V(j-1)]-[V(j)]为节点j处的剪力,由两个相邻的单元计算得来。[Vj]和[V(j)]分布为节点j和单元j的剪力。
如果同一段缆索均质且截面积不变,那么
(15)
式中:g为重力加速度,假设缆索单元的重量均分给两端的节点。
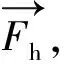
2 缆索单元的外载荷
缆索单元主要承受浮力、水流阻力、与附加质量相关的辐射力,于是缆索单元的外载荷可表示为
(16)

缆索单元的浮力矩阵可表示为
(17)
式中:ρw为水的密度;Acj为缆索的等效截面积;Lj为缆索单元的长度。
缆索受到的水流阻力是随着缆索位型改变而变化的,因此水流阻力是与时间相关的矩阵,可表示为
(18)
(19)
(20)
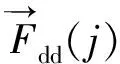
3 缆索的刚度矩阵与动力学方程
弯曲刚度矩阵可由剪力求导直接得到
[dV(j)]=[T]T[u]=-[Kb][u]
(21)
将式(13)带入式(21),于是有
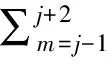
(22)
(23)
(24)
单元j的轴向弹性力可由两个节点的位移来确定,即
(25)
式中:[Ka]为缆索轴向刚度矩阵,为6*6的矩阵。
(26)
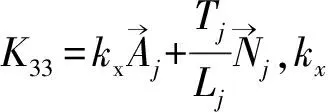
最后,联立式(14)、式(16)、式(22)和式(25),可以将方程演变为时域分析缆索动力学方程的通用形式

(27)
式中:[M]为总的质量矩阵(包括结构质量和附加质量);[C]为线性阻尼矩阵;[Ftotal]为缆索受到的合力矩阵。于是根据式(27)可解得缆索的空间位型结果,再将缆索空间位型带入式(1)和(2)可以得到张力、剪力和弯矩等结果。
4 算例分析
4.1直航运动
采用Rispin拖曳系统的实验模型[3]作为算例。该拖曳缆索由6段组成,各段缆索的参数见表1,实验缆索模型如图2所示。直航实验中拖船保持匀速,航速分别为5.14 ms和9.52 ms,计算缆索稳定后拖点倾角和拖缆阵列A点处的水深,数值结果与实验结果对比见表2。
从表2的结果可以看出,匀速直航状态下拖曳缆索的数值结果与Rispin实验结果[3]匹配较好。
图2 实验缆索模型Fig.2 Cable model of test
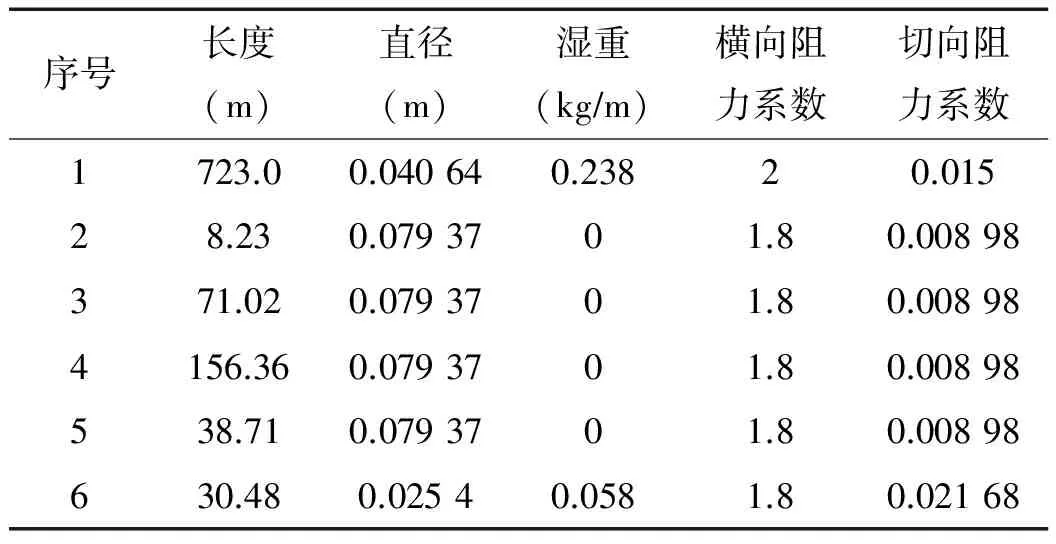
序号长度(m)直径(m)湿重(kg∕m)横向阻力系数切向阻力系数1723.00.040640.23820.01528.230.0793701.80.00898371.020.0793701.80.008984156.360.0793701.80.00898538.710.0793701.80.00898630.480.02540.0581.80.02168
4.2水平正弦运动
为了验证拖船横向运动时缆索动力响应的准确性,采用Kennedy的实验模型[4]作为算例。该实验中拖船保持横向正弦运动,船尾悬挂直径为16 mm的钢质缆索,缆索的参数见表3。在船底和缆索末端装有水听器,用来测量缆索末端的响应幅值。

表2 直航算例缆索数值结果与实验结果[3]对比Tab.2 Result of simulation and experiment at stand-on vessel

表3 横向正弦运动算例缆索参数[4]Tab.3 Cable parameter at transverse sinusoidal moving vessel
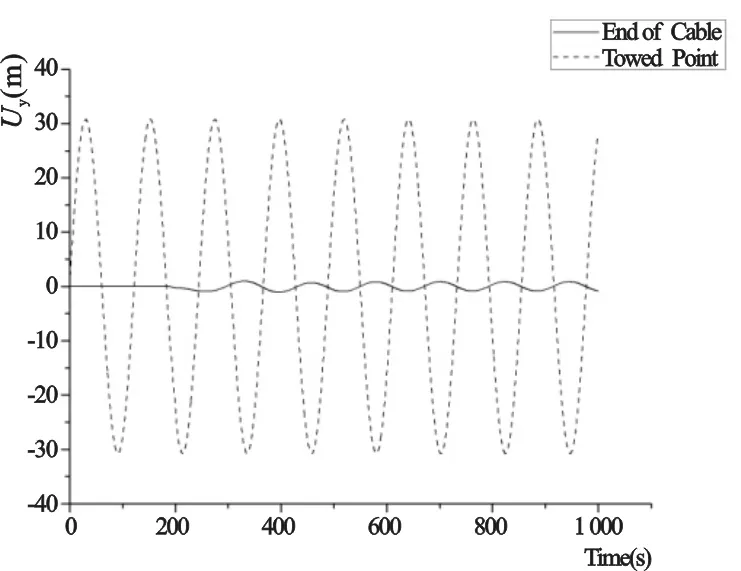
图3 算例5 (高频激励) 缆索Uy时间历程曲线Fig.3 Time history curve of cable Uy in case 5

图4 算例10 (低频激励) 缆索Uy时间历程曲线Fig.4 Time history curve of cable Uy in case 10
从表4的数值结果与实验结果对比可知,两者吻合较好。图3和图4分别是算例5和10的缆索拖点与末端横向位移的时间历程曲线。缆索末端随着拖船的横向正弦运动,也发生横向运动。缆索末端横向运动充分发展后,基本呈正弦运动规律。
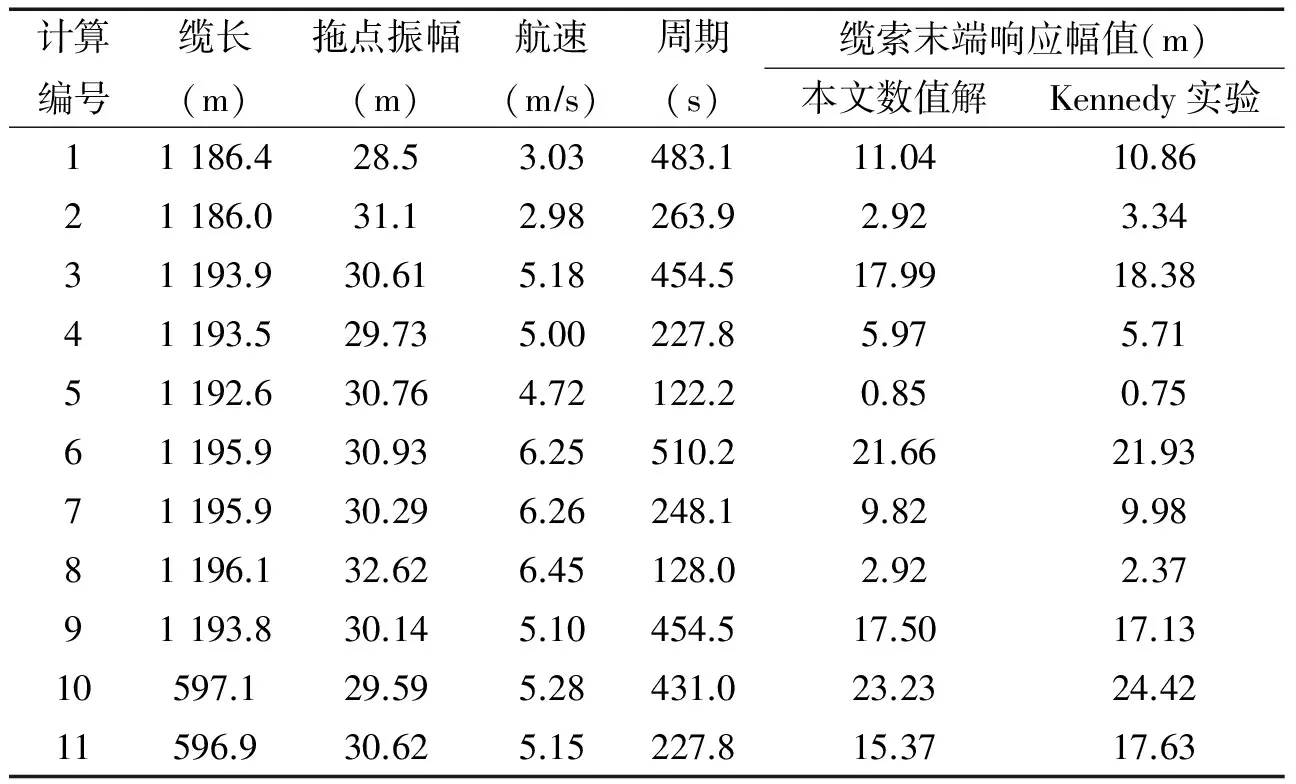
表4 横向正弦运动算例缆索数值结果与实验结果[4]对比Tab.4 Result of numerical simulation and experiment at transverse sinusoidal moving vessel
从表4中看出,本文数值结果与Kennedy实验结果[4]匹配较好。
对比图3和图4的结果,在振幅相当条件下,拖点激励频率越高,则缆索末端的响应幅值越小;缆索越长,其末端响应相比激励的滞后时间越长。
4.3升沉正弦运动
采用Rispin实验模型作为计算对象,假设母船只发生升沉正弦运动。定义动载荷系数为拖点最大张力除以稳态张力。模拟不同振幅和不同周期的母船位移激励下, 计算动载荷系数以及拖缆A点的升沉运动幅值的响应。
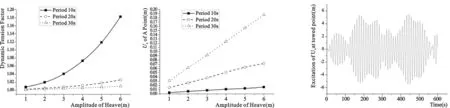
图5 动载荷系数响应 图6 拖缆A点的升沉运动幅值响应图 7 拖点激励的升沉运动时间历程曲线 Fig.5 Dynamic load factor Fig.6 Uz amplitude of towed cable A point Fig.7 Time history curve of UZ at towed point
从图5和图6的结果可知,母船升沉运动周期越大,缆索的位移扰动更易传播,但是动载荷系数随着运动周期的增大而减小,显然高频激励更易使缆索的动态张力增大。母船升沉运动振幅越大,缆索的位移扰动和动载荷系数均明显增加。
4.4升沉不规则运动
采用Rispin实验模型作为计算对象,给定一段不规则的持续600 s的母船拖点升沉运动载荷信号,升沉运动的最大幅值接近6 m,如图7所示。
计算结果与升沉规则运动的最大幅值也为6 m的情况进行比较可知,母船拖点的不规则运动使缆索的张力峰值显著增加,如表5所示。因此在评估拖曳系统的缆索张力问题时,母船的不规则运动的影响不可忽略。
表5各摇动状态下缆索拖点处张力的幅值
Tab.5 Towed maximum tension at regular and irregular moving ship kN

船舶规则升沉运动幅值6m周期10s周期20s周期30s船舶不规则运动最大幅值6m36.131.230.747.3
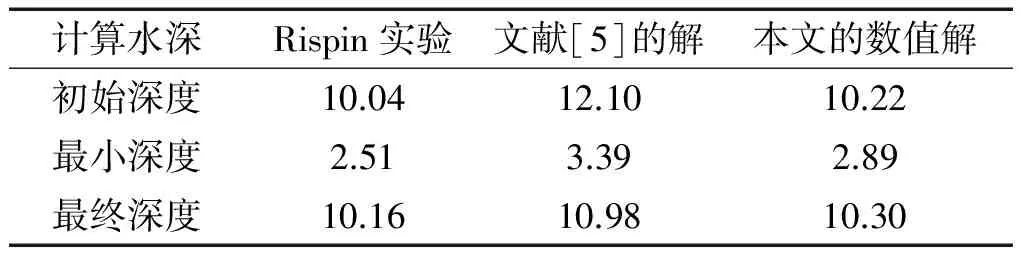
表6回转运动算例缆索数值结果与实验结果[3]对比
Tab.6 Result of numerical simulation and experiment at revolving moving vessel m
计算水深Rispin实验文献[5]的解本文的数值解初始深度10.0412.1010.22最小深度2.513.392.89最终深度10.1610.9810.30
4.5圆周回转运动
在Rispin的拖曳回转运动实验中,拖船先以18.5 kn的航速直航,然后进入回转半径为640 m的回转中,回转角度375°(440 s),回转结束后沿圆周切向作稳定直航(300 s),整个过程耗时12 min20 s。本文的数值解与Rispin实验结果比较见表6。
从表6的结果可以看出,回转运动下缆索深度的数值结果与Rispin实验结果[3]匹配情况,相比文献[5]的结果更好。
5 结论
基于集中质量法,推导了拖曳缆索动力学方程,全面地考虑了缆索的外载荷,包括重力、浮力、横向与切向水流力以及辐射力,同时考虑了缆索的拉伸和弯曲刚度。编制了相关计算程序,模拟了拖船匀速直航、横向正弦运动、升沉运动、回转运动下缆索系统的动力响应。得到如下结论:
(1)从匀速直航运动和水平正弦运动的算例可以看出,本文的模拟结果与实验结果吻合较好,说明本文给出的计算方法能较为准确地预报缆索的受力与运动姿态;
(2)水平正弦运动中,在振幅相当条件下,拖点激励频率越高,则缆索末端的响应幅值越小;缆索越长,其末端响应相比激励的滞后时间越长;
(3)升沉正弦运动中,缆索拖点张力和缆索振幅均随着母船运动幅值增大而增大,母船升沉运动周期增大时,缆索的位移扰动更易传播;
(4)相比规则运动。母船的不规则运动使拖曳缆索的张力峰值明显增加,实际缆索的张力与强度计算时,需要考虑母船不规则运动的影响;
(5)回转运动下,相比采用有限差分法的文献[5]结果,本文的数值结果与实验结果匹配更好。
[1]Choo Y, Casarella M J. A Survey of Analytical Methods for Dynamic Simulation of Cable-Body Systems[J]. Journal of Hydronautics, 2012, 7(4):137-144.
[2]Russell J J, Anderson W J. Equilibrium and Stability of a Circularly Towed Cable Subject to Aerodynamic Drag[J]. Journal of Aircraft, 1976, 14(7):680-686.
[3]Ablow C M, Schechter S. Numerical simulation of undersea cable dynamics[J]. Ocean Engineering, 1983, 10(6):443-457.
[4]Kennedy R M, Strahan E S.A linear theory of transverse cable dynamics at low frequencies[R].NUSC Tech. Rep. 6463, Naval Underwater Systems Center, Newport, Rhode Island New London, Connecticut,1981.
[5]李力波. 海下缆索系统运动的动力学模拟[J]. 中国造船, 1989(4): 33-44. LI L B. Dynamic simulation of underwater cable system motion[J]. Shipbuilding of China,1989(4):33-44.
[6]朱克强, 李道根. 海洋缆体系统的统一凝集参数时域分析法[J]. 海洋工程, 2002, 20(2): 100-104. ZHU K Q, LI D G. Lumped parameter analysis method for time-domain of ocean cable-body systems[J]. The Ocean Engineering, 2002, 20(2): 100-104.
[7]朱艳杰, 朱克强, 杨冰卡,等. 基于凝集质量法的海洋缆索动力学建模与数值技术[J]. 海洋工程, 2014, 32(1):112-116. ZHU Y J, ZHU K Q, YANG B K, et al. Dynamics modeling and emulation technique of the marine cable considering tension and compression bending torsion deformation[J]. The Ocean Engineering, 2014, 32(1): 112-116.
[8]王志博, 侯德永. 拖曳系统运动传递计算[J]. 船舶力学, 2015, 19(4): 389-396. WANG Z B, HOU D Y. Towed system motion transfer calculation[J]. Journal of Ship Mechanics, 2015, 19(4): 389-396.
Dynamic response analysis of the undersea towed cable based on lump-mass method
LIUMing,LIJia-wang,ZHUKe-qiang
(FacultyofMaritimeandTransportation,NingboUniversity,Ningbo315211,China)
To study the undersea towed cable system, equation of dynamic cable was deduced based on lump-mass model. Nonlinear dynamic response analysis of towed cable was carried out based on 4th order Runge-Kutta integration algorithm. The motion and force of towed cable were simulated by a computer program under the condition of ship moving forward with constant speed, transverse sinusoidal motion, heave and revolving moving. From comparison of numerical analysis and experiment, it indicates that lump-mass model is applicable under cable motion excitation of various boundary conditions. Simulation results of lump-mass model compare better with the test than the results of finite difference method.
lump-mass method; undersea towed cable; dynamic response
TV 139.2;O 242.1
:A
:1005-8443(2017)04-0405-07
2016-11-07;
:2017-01-06
国家自然科学基金 (11272160);国家自然科学基金青年项目(51309133)
刘铭(1989-),男,辽宁省锦州人,助理研究员,主要从事船舶与海洋结构物动态响应的研究。
Biography:LIU Ming(1989-),male, assistant professor.

