基于支持向量机的连续超声图像集分割算法

刘 俊，李鹏飞

(武汉科技大学 计算机科学与技术学院，武汉 430081) (*通信作者电子邮箱807657578@qq.com)

基于支持向量机的连续超声图像集分割算法

刘 俊，李鹏飞*

(武汉科技大学 计算机科学与技术学院，武汉 430081) (*通信作者电子邮箱807657578@qq.com)

针对传统的支持向量机(SVM)模型对连续超声图像集进行分割时需要为图像集中每张图片提取样本点来建立分割模型的问题，提出了一个对整个连续超声图像集的统一的SVM分割模型。首先，从图像的灰度直方图中提取灰度特征作为表征图像集中图像连续性的特征；其次，从图像集中选取部分图像作为样本，并从中提取像素点的灰度特征；最后，将各像素点的灰度特征与各像素点所在图像中表征图像集连续性的特征相结合，用SVM的方法训练出分割模型对整个图像集进行分割。实验结果表明，与传统SVM分割方法相比，新模型在面对大量的有连续变化的图像集的分割问题上，大幅地减少了人工选取样本点的工作量，并且在分割的准确率上也有保证。

支持向量机；图像分割；图像集分割；机器学习；特征提取

0 引言

图像分割是图像分析和处理中重要的一步。而图像分割的过程，其实也是图像中像素点聚类的过程。而随着对图像分割准确率要求的提高，传统的阈值分割、边缘分割以及水平集分割算法的分割能力就显得力不从心，因此为了得到更好的聚类结果，机器学习中的一些聚类理论就应用在了图像分割中。例如，模糊C均值聚类、马尔可夫随机场以及支持向量机(Support Vector Machine, SVM)。

SVM作为一种有监督的机器学习方法，是Vapnik在1995年为了检测入侵数据提出的一种方法。该方法通过核函数将低维线性不可分的数据映射到高维空间，使得在高维空间找到能将数据分割的超平面，而此超平面就是对其他数据进行分类的分类器。而支持向量机在基于统计学理论的基础上又与松弛变量技术相结合，使得其在误差处理方面表现良好，因此越来越多的学者发现SVM在图像分割上的优势，并展开了深入的研究。如：文献[1]将像素点及其周围邻域像素点的灰度值排列成特征向量进行训练，该方法将图像最基本的像素值作为特征，特征提取简单，对像素对比度高的图像有很好的效果，但不适用于边缘对比度低的超声图像；文献[2]则提取图像的纹理和色彩作为训练的特征向量，对具有规则纹理的彩色图像具有良好的分割效果，但同样不适用于变化不规则的灰度图像；文献[3]通过提取图像中一种改进的超矩形进行训练得到SVM模型，该方法通过提取形状特征来处理一些不需要精确分割的实时问题；文献[4]通过提取子块的灰度均值和灰度标准差作为特征，该方法提取子块的灰度统计特征，能在一定程度上反映图像的灰度变化，但子块的大小选取对图像的分割结果有较大的影响；文献[5]将图像的相位一致性与灰度特征结合起来训练图像，相位一致性能较好地反映图像像素的频率特征，但特征提取较为复杂；文献[6]则提出了一种区域增长和SVM相结合的分割方法，该方法将区域增长和SVM的优点相结合，在联通区域良好分类的情况下，保证了较好的边缘信息，但是依然存在区域生长中效率低下的问题。以上学者通过提取图像中不同的特征，训练出不同的SVM图像分割模型，而这些模型的训练样本都是从单张图片中提取的，得到的模型只能对相应图片进行分割。对于大量的连续的图片，使用上述模型分割时，就需要对每张图片进行人工的样本提取，为每张图片训练出单独的分割模型。这种行为不仅耗费人力，而且由于需要人为地对训练样本进行分类，过于依靠人为经验，增大了分割的风险和误差。

针对医学处理中大量的连续的超声图像集，本文结合图像的整体灰度特征与图片中像素的灰度特征，只对大量连续图片中的部分图片提取样本，训练出了一个可以对整个图像集进行分割的SVM模型。而对于超声图像边缘对比度低、噪声干扰大的特点[7]，本文首先要对图像进行预处理，提取囊括主要目标区域的图像块。然后从图像块的灰度直方图中提取灰度特征，作为图像的整体灰度特征。本文再根据连续图像灰度特征的变化规律，将整个图像集按其连续性排列成一个由多幅图像组成的大图像，而对一个图像提取样本点，就相当于在整个图像集中选取部分图像。然后，再从选出的图像中提取样本点，将样本点的特征与对应图像的整体特征相结合，就得到了整个图像集的统一分割模型的训练样本。由于图像的整体灰度特征可以由计算机运算得到，而图像中样本点则需要依靠人为经验进行选取和分类。这样就增加了计算机所需完成的工作而减少了选取样本点所需要的人为工作量。最后，将得到的模型对图像集中所有图片进行分割，就得到了最终的结果。

1 传统的SVM分割模型

SVM是一种通过最小化经验风险和置信范围来优化分类器分类能力的机器学习方法，因其对小规模样本也能获得良好的统计规律，在20世纪90年代中期开始兴起，现在广泛应用于分类和回归问题，而图像分割的问题也是一种将图像中的像素点进行分类的问题。对于一张图像I，设I(m,n)为图像中第m行n列的像素点，x(m,n)为I(m,n)像素点的某种特征向量。传统的SVM分割算法通过从已分类的训练样本集Itrain中提取对应的特征集合X，然后通过寻求最大几何间隔γ来确定分类器函数中的参数w和b，最大几何间隔γ求法如下[8]：

maxγ=max (1/‖w‖)

s.t.yi(wTxi+b)≥1;i=1,2,…,s

(1)

其中yi为Itrain中像素点的分类标签，s为训练样本的个数，并假设：

(2)

因此，yi(wTxi+b)≥1(i=1,2,…,s)就表示Itrain所有点分类正确且其到分类超平面的几何间隔都不小于最大几何间隔γ[9]。最后用训练得到的分类器f(x)对整张图片I的所有像素进行分类，便得到了本文的分割结果。

从上文中可以看出：由于传统的SVM分割算法只提取图片中像素点的特征，因此训练出来的分割模型只能对提取训练样本的图片进行分割；面对连续变化的图像集，传统的SVM分割算法只能为图像集的每张图片训练一一对应的模型进行分割，也就意味着需要对每张图片进行样本提取，耗费大量人力。

2 一种基于连续图像集的SVM分割模型

本文充分利用此类图像集连续性变化的特点，提出了一个对整个图像集的统一分割模型。其实传统的SVM分割模型也是利用了像素点的特征变化存在连续性的特点，比如像素点的灰度特征：由于图片中相同区域的像素点的灰度值的变化是一个连续的、渐变的过程，因此把像素点的灰度值作为特征向量进行训练。而对于一个连续的图像集，可以将每张图像当作一个块，把某些能表示图像集连续性的特征提取出来。然后依据这些特征，将这些作为块的图像排列起来，也即是将一整个图像集中所有图片按某种规则排列，组成一个更大的图像。然后从这个组合图像中提取像素点作为样本，将像素点的特征与像素点所在图像块的特征相结合，组成一个新的样本特征进行训练，于是就得到了一个可以对整个图像集中所有图片进行分割的模型。

在对单张图像通过提取单个像素点的灰度值作为训练样本时，并不需要将一幅图像所有不同灰度值的像素点都提取出来作训练，这是因为其灰度变化存在连续性。于是对于这个由连续图像块组成的代表整个图像集的大图像，也不需要对每个图像块都进行样本的提取，于是便减少了人工提取样本点的工作量。图1分别是传统的SVM分割模型和本文提出的对于图像集的SVM分割模型的流程。

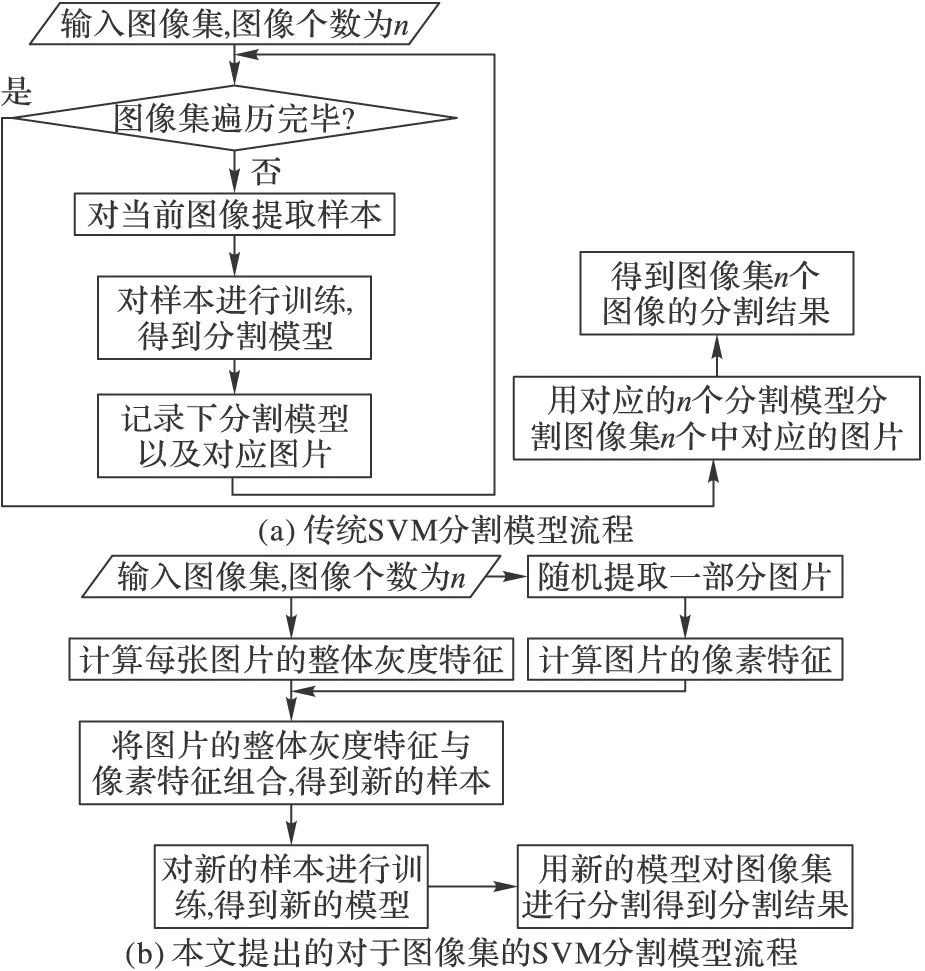
图1 两种不同分割模型的流程

从图1可以看出，不论是传统SVM分割模型还是本文提出的模型都需要从样本图像中提取特征，因此图像的特征提取是SVM分割模型中重要的一步。图像的特征多种多样，既有图像整体特征，也有图像的局部特征，各种特征都有其适用范围和优缺点，因此针对不同的图像，要根据其特点选择合适的特征进行提取。下一章将探讨针对本文所研究的超声图像的特征提取问题[10]。

3 特征提取

3.1 图像的整体灰度特征

为了表示本文研究的超声图像集的连续性，本文将图像整体的灰度特征提取出来代表图像集中每幅图像的特征，图像整体的灰度特征反映了整幅图像中各灰度级的分布以及均匀程度。本文通过提取图像的灰度直方图来表示图像各灰度级的统计特性，再从灰度直方图中计算出均值、方差、偏度和峰度来表征各灰度级的分布特性[11]。

假设现有一幅灰度图像I，该图像有L个灰度级，ni表示图像中第i个灰度级像素点的个数，则图像的灰度直方图用下面的式子定义：

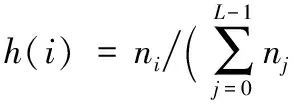
(3)

由式(3)可知，灰度直方图就是一个离散函数，反映了各灰度级在图像中出现的频率。为了更好地表示灰度直方图中的信息，使得提取的灰度特征得到更好的表征，本文要利用到数学工具中的高阶矩[12]。

在统计学中各阶矩都有其对应的意义，一阶矩表示均值，反映图像的平均灰度值，如式(4)：

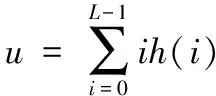
(4)

二阶矩表示方差，反映图像上各灰度级之间的离散情况，如式(5)：

(5)

三阶矩表示偏度，反映图像灰度级的不对称程度，偏度值越大，灰度直方图的中间灰度值的左右两边越不对称，反之偏度值小，则越对称，其公式表示如式(6)：

(6)

四阶矩表示峰度，反映了图像在均值灰度处的分布情况。峰度越大，在均值灰度处的像素分布数量越多，峰度越小，则像素分布数量越少，如式(7)：

(7)

由于本文研究的超声图像集存在的噪声干扰大、边缘灰度对比度低的问题，直接从图像中提取特征不能很好地表征图像的信息[13]，因此本文在进行图像整体灰度特征提取之前，需要对图像进行预处理。

首先通过双峰法在图像的灰度直方图中寻找一个合适的阈值来对图像进行初步的分割。但是由于超声图像灰度对比度低、灰度一致性较差，其灰度直方图随机波动较大，难以计算其波峰所在灰度级，所以要对初始的灰度直方图进行平滑处理[14-15]。假设原始的灰度直方图为式(3)中所定义的h(i)，平滑的规格系数为ε,那么平滑处理后的灰度直方图h2表示如式(8)：

(8)

平滑处理过后的灰度直方图虽然消除了一部分的随机波动，但还是会出现多波谷的问题，因此要利用多个位于波谷位置的灰度级来计算出一个合适的灰度级作为阈值，从而对图像进行初始分割。

假设在两个波峰之间找到了ξ个波谷，设其所在灰度级为tr(p)(p=1,2,…,ξ)，则其灰度级所对应像素点出现的概率为h2(tr(p))(p=1,2,…,ξ)。利用加权平均的方法，像素点出现概率越小的灰度级权值越大，来计算出作为阈值的灰度级。设每一个位于波谷灰度级的权值为θp，则有：

(9)

则作为阈值的灰度值th的计算公式如式(10)：

(10)

在对初始分割后的图像进行形态学上的膨胀处理，膨胀系数视图像边缘对比度的模糊程度来定，边缘模糊程度大、对比度低，则膨胀系数大；反之，则膨胀系数小。膨胀处理的目的是为了使处理过后的图像块能够将整个目标区域及一定程度上的背景区域囊括起来，这样有两个好处：

1)不会因为初始分割的阈值计算误差损失目标区域的灰度信息，处理后的图像块更能代表该图像。图2为本文所使用的卵泡超声图像集中某图片所对应的h2,h3的函数图像，可见h3与h2相比，去掉了大部分背景部分的灰度信息，不仅减少了超声图像中大量的噪声干扰，也使目标区域的灰度信息更为明显。而对于本文以及大部分的图像集来说，图像集变化的连续性是由目标区域变化的连续性来体现的，因此，本文将膨胀处理过后的图像块的灰度直方图h3作为提取整个图像灰度特征的灰度直方图。

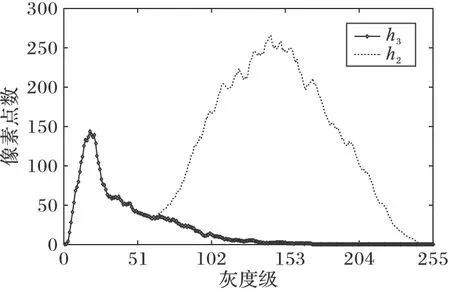
图2 某卵泡超声图片两种不同的函数

2)从图像块中提取的样本集拥有更小的最大几何间隔γ。上文提到SVM模型通过求训练样本的最大几何间隔，使得分类器具有最大确信度。而本文将在预处理之后得到的图像块上提取训练样本，使得背景区域的样本点更逼近边缘部分，即支持向量更接近分类超平面，缩小了训练样本的最大几何间隔，一定程度上增强了分类器对模糊边缘的分割能力[16]。

3.2 图像像素的灰度特征

图像像素的灰度特征就是图像中各像素点灰度值的大小，也有学者将像素点周围邻域的像素点灰度值一起作为该像素点的灰度特征。图像的灰度特征反映了图像的亮度变化，本文中按照下述方法提取图像像素的灰度特征。

假设gray(x)表示像素点x的灰度值。以该点为中心点取一个k×k的矩形区域，其中k为奇数，因此可以得到包括中心点在内k2个像素值，将这k2个像素值按顺序排列，记作Gk(x)，作为该像素点的灰度特征。而当m=1时的图像像素的灰度特征就是单个像素的灰度值gray(x)，这是一种特殊情况。

3.3 特征组合

在3.1节和3.2节中提取了图像的整体灰度特征和图像像素的灰度特征，现在需要将两种特征进行组合以方便后续工作中处理。

假设现在要对一组有α张图像的图像集进行样本提取。先把每张图片按3.1节的方法预处理，然后提取该图像的均值u、方差σ、偏度u3和峰度u4。然后从该图片中提取像素点，并记录其像素特征G。设图像的整体灰度特征为T，那么T=(u,σ,u3,u4)，即图像的均值、方差、偏度和峰度的线性组合。再将图像像素的灰度特征G与其对应图像的整体灰度特征T进行线性组合，得到本文中所需要的训练特征，设为R,那么R=(G,T)。这样就把两种特征组合起来了。

而此时已经将本文所需要的特征提取出来了，并进行了组合。下一步便是SVM的关键所在，通过核函数将线性不可分的特征向量从低维空间映射到高维空间，使其在高维空间中能找到一个超平面将提取的特征向量分离开来。而在将特征向量映射之前，还需要将特征向量进行归一化，以便于计算机对数据的处理。接下来着重探讨了核函数以及归一化的问题。

4 核函数与归一化

4.1 核函数

通过对图像进行特征提取，就得到了该图像的特征向量，即式(1)中的x。但是式(1)中的求解方法是在样本的特征数据线性可分的情况下，面对线性不可分的数据，就需要引入核函数将问题推广到高维，然后在高维空间中寻找线性可分的超平面。SVM中常用的核函数有线性核函数、多项式核函数和高斯核函数。其中高斯核函数适应性好，对没有先验知识的数据可以得到较为平滑的估计[17]，所以本文选择高斯核函数，其具体公式：

(11)

而高斯核函数性能的好坏，很大程度上取决于尺度参数σ的大小[18-19]，因此为了选择合适的尺度参数σ，需要用本文的训练样本来测试分割模型的准确率，即进行交叉验证[20-21]。在不停地迭代中，不断优化参数。

4.2 归一化

由于提取的特征向量x中各列特征的数值范围不同，为了保证在上文提到的参数寻优中，收敛更快、数据处理更方便，需要对特征向量进行归一化，将特征向量各元素控制在一定的范围内[22]。归一化公式如下：

(12)

5 实验结果与分析

5.1 仿真环境

实验基于的硬件环境为Intel Core i5- 6300HQ CPU 2.30 GHz,RAM 8 GB的个人笔记本电脑。本文所采用的分割算法以及对比实验均是在Matlab R2015a软件上模拟运行的。

5.2 两种模型对图像集的分割结果

本文的实验样本是100张150×200分辨率的黄牛卵泡超声图像集。先计算出100张图像的整体灰度特征，将其归一化，再把归一化后的特征记为T。再从图像集的每张图像中选取10个目标区域点和10个背景区域点，记录下k=1，3，5时的邻域点的灰度值作为图像像素点的灰度特征，归一化后分别记为G1，G3，G5。再将各像素点的灰度特征G与其对应图像的整体灰度特征T组合起来，记作R1=(T,G1)，R3=(T,G3)，R5=(T,G5)。

从图像集中随机抽取20张图像，分别用其特征R1，R3，R5作为训练样本。先对3个训练样本进行参数寻优，得到其最优的惩罚因子c和参数g，表1为其各特征对应的最优参数。

表1 各特征对应的最优参数

然后将各训练样本用对应的核函数进行训练，得到3个不同的训练模型。然后对图像集中所有图片用3种模型分别进行分割，得到3种不同的分割结果。然后再用传统的分割方法，将G1、G3、G5作为训练样本为每一张图像训练出单独的模型,这样又得到了另外3种模型。图3为图像集中某张图片被各种不同模型分割的结果。

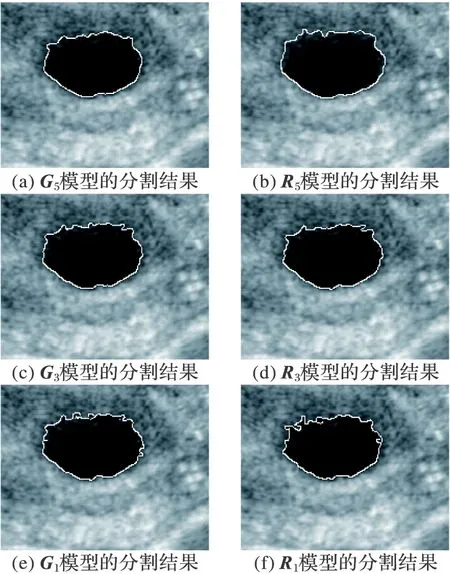
图3 各模型对卵泡图像的分割结果

为了得到客观的评价标准，本文引入Dice相似系数[23]，如式(13)所示：

(13)

并且为了描述训练出来的分割模型对整个图像集的分割准确率，本文引入了平均分割准确率。假设一个图像集中含有α张图像，DSCi为第i张图片的Dice相似系数，则平均分割准确率的公式为：

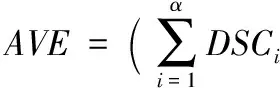
(14)

其中：R表示实验得到的分割区域的集合，S表示医生手动框选的目标区域的集合。将各模型对图像分割的结果与医生手动框选的卵泡区域进行比较，表2为各模型对整个图像集中所有共100张图片的分割平均准确率。

表2 各模型对图像集的平均分割准确率 %

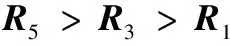
本文提取图像的整体灰度特征只是为了表示图像集中图像的连续性。不同种类的图像集，表示图像连续性的特征不同。而对同一种类的图像集，也可以用不同的特征表示其图像的连续性。比如本文除了可以用图像的整体灰度特征来表示图像的连续性，也可以用上文中预处理之后图像块的面积大小表示，将面积大小特征记为S。再将特征S与特征G组合起来，记作D1=(S,G1)，D3=(S,G3)，D5=(S,G5)。

与上文一样，随机抽取20张图像作为训练样本。提取图像中各模型所对应的特征向量，并为其参数进行寻优，将参数代入核函数中对训练样本进行训练，得到分割模型。使用不同的分割模型得到不同的分割结果，计算其平均准确率。如表3所示。

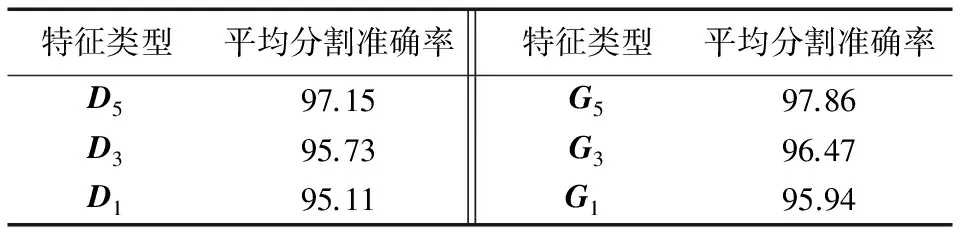
表3 第二次实验中各模型对图像集分割的平均准确率 %

从表3数据中可以得到与上文相同的结论。而将上面两个实验联系起来，发现不论用何种特征，只要此特征的变化能体现图像集中图像连续性的变化，那么就可以用到本文的模型中，因此对于不同种类的图像集，要针对此图像集的特点提取合适的特征来表征图像集的连续性。

5.3 训练样本占图像集比例与平均分割准确率的关系

上文的实验中在为本文所提出的模型选取样本时，都是从100张的图像集中随机抽取20张图像作为训练样本，即训练样本的数量占图像集的20%。当改变本文的训练样本所占图像集的比例时，训练出来的模型对图像集的分割准确率也会有所改变。按理论来说，当增大训练样本占图像集的比例时，训练出来的分割模型的分割准确率会增加；反之，当降低训练样本占图像集的比例时，分割的准确率也会相应减少，因此为了探究训练样本所占图像集比例与对应训练出来的分割模型对图像集分割准确率之间的关系，找到对于本文所用图像集来说较为合适的比例，为以后使用不同的图像集时提供一个参考。

改变训练样本所占比例，从图像集中随机抽取占图像集比例为10%、15%、20%、25%、…、55%、60%的图像作为不同的样本集，并且从样本集中提取D5，D3，D1作为训练特征进行训练。图4为用不同特征训练分割模型时样本比例与模型对图像集的平均分割准确率之间的关系。

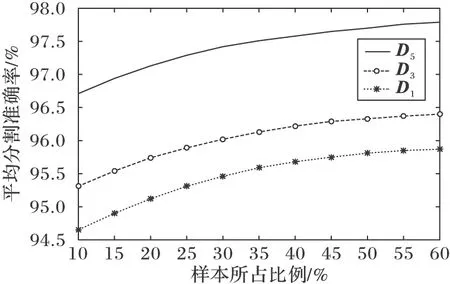
图4 各分割模型的样本比例与平均分割准确率之间的关系

从图4中可以看出，随着训练样本占图像集比例的增加，训练出来的模型对图像集的平均分割准确率也随之上升，但是增长速度逐渐变缓，因此在保证一定的分割准确率的前提下，使用本文提出的分割模型对图像集进行分割时，建议在抽取作为训练样本的图像时，其比例应占图像集的20%到35%为佳。

图5中为使用D5作为特征，在样本图像占图像集比例分别为10%、20%、30%、40%、50%和60%时所训练出来的分割模型对图像集中另一张卵泡图片的分割结果。

其对应的不同样本比例的模型对该图片的分割准确率分别为96.69%、97.07%、97.41%、97.58%、97.66%、97.71%。该结果所拟合的曲线与图4中D5曲线的变化趋势大致相符，说明了增加训练样本占图像集的比例，有助于提高训练出来的模型对图像的分割准确率，但是准确率的提高速度会逐渐变缓，因此在保证精度的前提下，选择合适的样本比例有助于减少提取样本的工作量。

为了验证该方法在其他图像集是否也能保证较高的平均分割准确率，本文再次使用D5作为特征，对另一图像集进行分割，并计算其在样本比例为10%、25%、40%、60%的平均分割准确率，其结果为96.38%、97.02%、97.23%，97.44%。图6为另一图像集中的一张图片的分割结果。

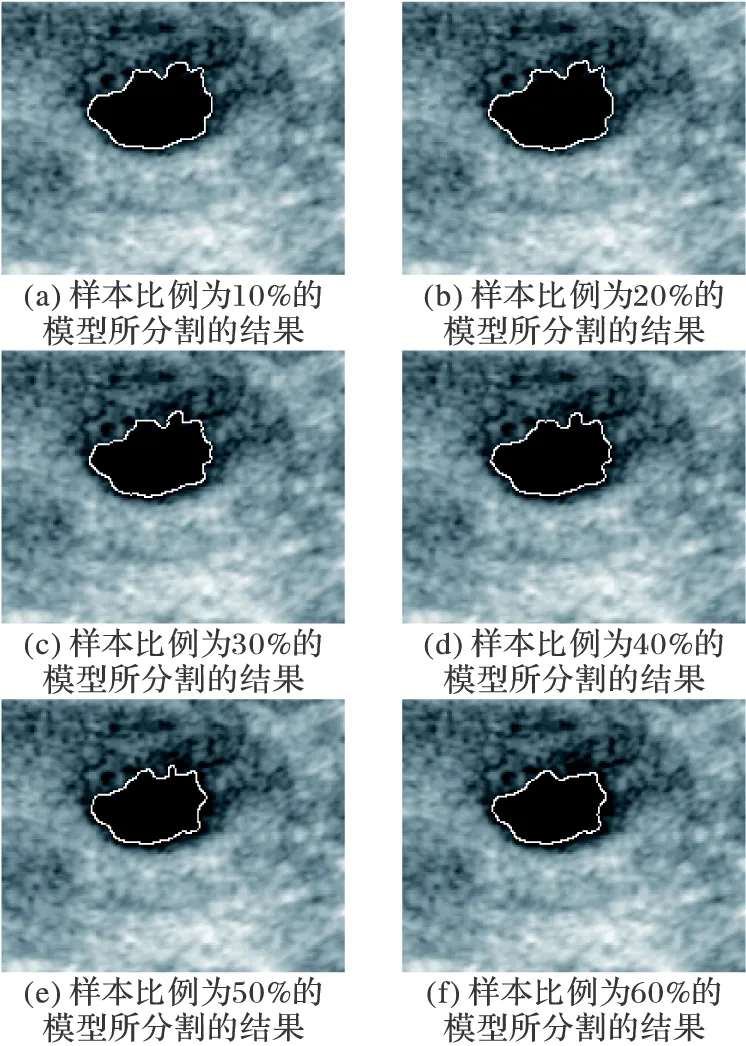
图5 不同样本比例的模型对卵泡图片的分割结果

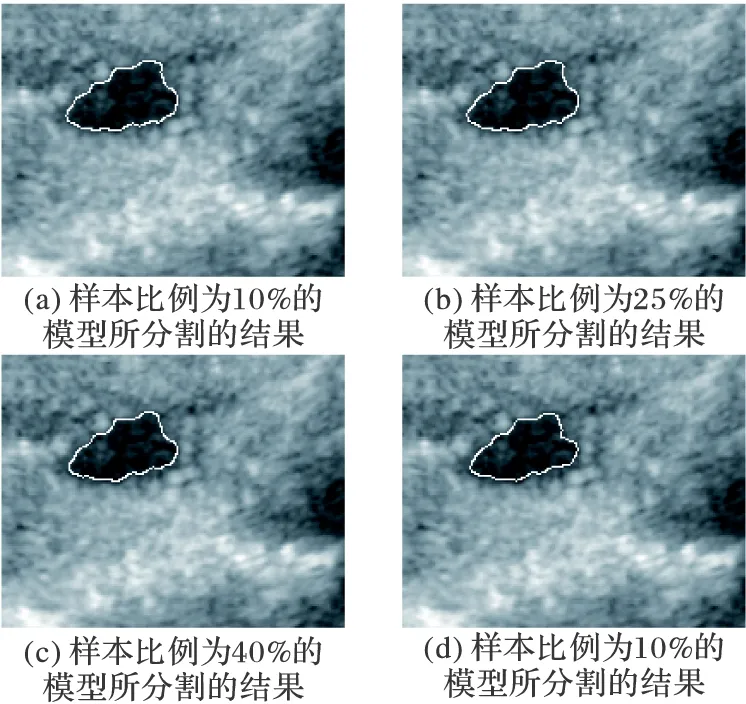
图6 不同样本比例的模型对另一图像集中图像的分割结果

与图4中的D5曲线以及图5中的图像的分割结果相比较发现，其分割准确率的数值都在96%到98%之间，因此本文方法对不同的图像集也有一定的适应性，并能保证较高的平均分割准确率。

6 结语

本文提出的一个对连续图像集的整体SVM分割模型与传统的SVM分割模型相比，通过将能表征图像集中图像之间连续性的特征提取出来，与表示图像中像素点的特征相结合，组成一个新的特征。而在使用新的特征提取样本时，就不需要对图像集中所有图像进行样本点的提取，减少了人工选取样本点的工作量。然而对于不同的图像集，表征图像集中图像连续性的特征可能不同，表征图像中像素点的特征也可能不同，因此并不能找到一个特定的特征来对所有图像集进行处理，于是在处理不同的图像集时，也应遵循该图像集的特点寻找合适的特征。

本文的不足之处在于，在图像集中随机抽取样本时候，在比例一定的情况下，每次抽取的样本却不一样。例如上面两个实验中同样是用D5、D3、D1作为特征进行提取，在同为20%的样本比例下，得到的平均分割准确率却不一样。虽然两次结果相差无几，但也证明了样本的选择对分割的准确率存在一定的影响，因此在确定了样本所占图像集比例的情况下，以何种方法选择样本，如何选择样本能使平均分割准确率提高，便是接下来要研究的问题。

References)

[1] REYNA R A, HERNANDEZ N, ESTEVE D, et al. Segmenting images with support vector machines [C]// Proceedings of the 2000 International Conference on Image Processing. Piscataway, NJ: IEEE, 2000, 1: 820-823.

[2] YANG H Y, WANG X Y, WANG Q Y, et al. LS-SVM based image segmentation using color and texture information [J]. Journal of Visual Communication & Image Representation, 2012, 23(7): 1095-1112.

[3] MITERAN J, BOUILLANT S, BOURENNANE E. SVM approximation for real-time image segmentation by using an improved hyperrectangles-based method [J]. Real-Time Imaging, 2003, 9(3): 179-188.

[4] CHEN X, TIAN J. Segmentation of fingerprint images using linear classifier [J]. EURASIP Journal on Advances in Signal Processing, 2004, 2004(4): 1-15.

[5] 邓晓飞,徐蔚鸿.一种结合多特征的SVM图像分割方法[J].计算机工程与科学,2013,35(2):154-158.(DENG X F,XU W H.An SVM image segmentation method using multi-features [J]. Computer Engineering & Science, 2013, 35(2): 154-158.)

[6] 薛志东，隋卫平，李利军.一种SVM与区域增长相结合的图像分割方法[J].计算机应用,2007,27(2):463-465.(XUE Z D, SUI W P, LI L J. Interactive segmentation method with SVM and region growing [J]. Journal of Computer Applications, 2007, 27(2): 463-465.)

[7] MICHAILOVICH O V, TANNENBAUM A. Despeckling of medical ultrasound images [J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control, 2006, 53(1): 64-78.

[8] 薛志东,王燕,李利军.SVM图像分割方法的研究[J].微计算机信息,2007,23(24):306-308.(XUE Z D, WANG Y, LI L J. The research on SVM segmentation method [J]. Microcomputer Information, 2007, 23(24): 306-308.)

[9] MITRA P, SHANKAR B U, PAL S K. Segmentation of multispectral remote sensing images using active support vector machines [J]. Pattern Recognition Letters, 2004, 25(9): 1067-1074.

[10] 曹健,李海生,蔡强,等.图像目标的特征提取技术研究[J].计算机仿真,2013,30(1):409-414.(CAO J, LI H S, CAI Q, et al. Research on feature extraction of image target [J]. Computer Simulation, 2013, 30(1): 409-414.)

[11] 郝衍,朱信忠,赵建民,等.基于图像颜色直方图及纹理特征提取的兴趣点凸包检索方法[J].微型电脑应用,2011,27(6):42-45.(HAO Y, ZHU X Z, ZHAO J M, et al. Home point retrieval method based on color histogram and texture feature extraction [J].Microcomputer Applications, 2011, 27 (6): 42-45.)[12] PATRICIO M A, MARAVALL D. Segmentation of text and graphics/images using the gray-level histogram Fourier transform [C]// Proceedings of the 2000 Joint IAPR International Workshops on Statistical Techniques in Pattern Recognition (SPR) and Structural and Syntactic Pattern Recognition (SSPR). Berlin: Springer, 2000: 757-766.

[13] BAI X, WANG W. Saliency-SVM: an automatic approach for image segmentation [J]. Neurocomputing, 2014, 136(8): 243-255.

[14] HUTCHINSON M F, HOOG F R D. Smoothing noisy data with spline functions [J]. Numerische Mathematik, 1985, 47(1): 99-106.

[15] 芮杰,吴冰,秦志远,等.一种稳健的自适应图像平滑算法[J].中国图象图形学报,2005,10(1):54-58.(RUI J, WU B, QIN Z Y, et al. A robust adaptive image smoothing algorithm [J]. Journal of Image and Graphics, 2005, 10(1): 54-58.)

[16] 彭新俊,王翼飞.间隔v-支持向量机及其几何问题[J].模式识别与人工智能,2009,22(1)：8-16.(PENG X J, WANG Y F. Total marginv-support vector machine and its geometric problem [J]. Pattern Recognition & Artificial Intelligence, 2009, 22(1): 8-16.)

[17] 奉国和.SVM分类核函数及参数选择比较[J].计算机工程与应用,2011,47(3):123-124.(FENG G H. Parameter optimizing for support vector machines classification [J]. Computer Engineering and Applications, 2011, 47(3): 123-124.)

[18] 卢照敢,许春梅,孙楠,等.采用改进高斯核的MLS-SVM人脸表情识别算法[J].计算机科学,2014,41(s1):132-134.(LU Z G, XU C M, SUN N, et al. Improved face emotion identification algorithm by MLS-SVM with modified Gauss kernel function [J]. Computer Science, 2014, 41(s1): 132-134.)

[19] MCFEETERS S K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features [J]. International Journal of Remote Sensing, 1996, 17(7): 1425-1432.

[20] LI J, WANG H, LI S. Microscopic image segmentation method based on SVM [J]. International Journal of Signal Processing, Image Processing and Pattern Recognition, 2016, 9(2): 179-188.

[21] TIAN X, HU T. A method of debris image segmentation based on SVM [C]// IMSCCS’06: Proceedings of the First International Multi-Symposiums on Computer and Computational Sciences. Piscataway, NJ: IEEE, 2006: 307-311.

[22] 王行甫,陈家伟.基于高斯核的SVM的参数选择[J].计算机系统应用,2014,23(7):242-245.(WANG X F, CHEN J W. Parameter selection of SVM with Gaussian kernel [J]. Computer Systems & Applications, 2014, 23(7): 242-245.)

[23] MIZUSHIMA A, LU R. An image segmentation method for apple sorting and grading using support vector machine and Otsu’s method [J]. Computers & Electronics in Agriculture, 2013, 94: 29-37.

This work is partially supported by the National Natural Science Foundation of China (31201121), Innovation Fund of Wuhan University of Science and Technology (14ZRA082).

LIUJun, born in 1977, Ph. D., associate professor. His research interests include image processing, image segmentation, image detection, image denoising, machine learning.

LIPengfei, born in 1993, M. S. candidate. His research interests include image processing, image segmentation, machine learning.

Continuousultrasoundimagesetsegmentationmethodbasedonsupportvectormachine

LIU Jun, LI Pengfei*

(CollegeofComputerScienceandTechnology,WuhanUniversityofScience&Technology,WuhanHubei430081,China)

A novel Support Vector Machine (SVM)-based unified segmentation model was proposed for segmenting a continuous ultrasound image set, because the traditional SVM-based segmenting method needed to extract sample points for each image to create a segmentation model. Firstly, the gray feature was extracted from the gray histogram of the image as the characteristic representing the continuity of the image in the image set. Secondly, part images were selected as the samples and the gray feature of each pixel was extracted. Finally, the gray feature of the pixel was combined with the feature of image sequence continuity in the image where each pixel was located. The SVM was used to train the segmentation model to segment the whole image set. The experimental results show that compared with the traditional SVM-based segmentation method, the new model can greatly reduce the workload of manually selecting the sample points when segmenting the image set with large quantity and continuous variation and guarantees the segmentation accuracy simultaneously.

Support Vector Machine (SVM); image segmentation; image set segmentation; machine learning; feature extraction

TP751; TP391.413

:A

2017- 01- 05;

:2017- 02- 25。

国家自然科学基金资助项目(31201121)；武汉科技大学创新基金资助项目(14ZRA082)。

刘俊(1977—)，男，湖北武汉人，副教授，博士，主要研究方向：图像处理、图像分割、图像检测、图像去噪、机器学习； 李鹏飞(1993—)，男，湖北安陆人，硕士研究生，主要研究方向：图像处理、图像分割、机器学习。

1001- 9081(2017)07- 2089- 06

10.11772/j.issn.1001- 9081.2017.07.2089