三维扫描测头精确跟踪的摄影测量方法

刘 虹，王文祥，李维诗

(合肥工业大学 仪器科学与光电工程学院，合肥 230009) (*通信作者电子邮箱liuhong93@126.com)

三维扫描测头精确跟踪的摄影测量方法

刘 虹*，王文祥，李维诗

(合肥工业大学 仪器科学与光电工程学院，合肥 230009) (*通信作者电子邮箱liuhong93@126.com)

针对传统三维扫描测量机器人依赖于机器人的定位精度从而难以实现高精度测量的问题，提出了一种三维扫描测头精确跟踪定位的摄影测量方法。首先，搭建由多个工业摄像机构成的测头跟踪系统，并在机器人的扫描测头上粘贴编码标志点；然后，对摄像机进行高精度标定，求解出摄像机内外参数；其次，多摄像机同步采样，对图像中的标志点依据编码原理进行匹配，并求出投影矩阵；最终，求解出编码标志点在空间中的三维坐标，实现三维扫描测头的跟踪定位。实验结果表明，标志点定位在距离上的平均误差为0.293 mm，在角度上的平均误差为0.136°，算法精度在合理范围之内。采用该摄影测量方法可以提高扫描测头的定位精度，从而实现高精度测量。

工业机器人；三维扫描测头；编码标志点；摄影测量；跟踪

0 引言

制造业的生产方式正发生着深刻变革，为了降低生产成本、提高生产效率，特别是提高产品质量，工业机器人在工业现场的大规模使用已成为大势所趋。将三维扫描测头安装于工业机器人的手部，二者集成为一种自动化检测系统，本文将之称为三维扫描测量机器人，这类系统在汽车、航空、航天制造等领域中复杂曲面类零件以及产品的在线检测中已有应用。

传统的三维扫描测量机器人主要由三维扫描测头工业机器人构成，在测量过程中扫描测头的位置和姿态由机器人确定，因此测量精度依赖于机器人的定位精度。工业机器人本身一般采用串联开链式关节构型，其定位精度往往受到各种不确定因素的影响，比如机器人本身的惯性滞后、温度变形和各零部件之间的挤压变形等，这些因素导致的机器人定位误差累加起来就会限制其在高精度领域上的应用，特别是在检测领域的应用。研究表明，通过改善上述影响因素的方法来提高精度，作用十分有限[1]。

为了提高测量精度，目前三维扫描测量机器人一般采用测头跟踪系统。在测量过程中，机器人在程序的控制下带动扫描测头，根据规划出的测量路径在空间中运动，对被测工件进行扫描，测头跟踪系统同步测量扫描测头的位置和姿态，从而消除机器人对测量精度的影响。目前已有的激光跟踪仪跟踪系统[2]价格较高，而且容易出现遮挡，在测量复杂外形零件时一般需要多次转站，不适合用于复杂曲面类零件的在线测量。本文研究一种基于摄影测量原理的测头跟踪系统，在消除机器人对系统测量精度影响的同时，大幅提高测量范围并降低遮挡现象出现的几率。上述“遮挡”是指在测量过程中，跟踪系统与扫描测头之间出现遮挡物(包括操作人员)，跟踪系统无法“看见”扫描测头，因而无法跟踪扫描测头的位姿。

数字工业摄影测量技术作为工业测量技术的重要组成部分，在大尺寸、高精度、现场环境越来越复杂的工业现场发挥越来越重要的作用。从20世纪60年代开始便有学者对近景摄影测量的相关理论、算法及硬件进行研究，并逐步将其应用到工业测量领域。到90年代，随着计算机技术的快速发展和日益普及，工业摄影测量技术也有了长足的发展，并发展出摄像测量技术，用于动态测量。Hartley等[3]和Faugras[4]首先系统提出了基于多视图像的三维重建方法，建立了统一的立体视觉理论。基于这种理论，双目或者三目立体视觉可以看成摄影测量的一种特例。

本文基于多视图像的三维重建方法，将摄影测量技术应用于扫描测头的同步跟踪：首先提出了一种适用于扫描测头的点分布型编码标志点方案，在此基础上实现编码标志点的中心定位和匹配；然后基于摄像机的内外参数求出投影矩阵，进而计算出匹配点的空间三维坐标。利用匹配点的空间三维坐标可以确定测头的位置和姿态，从而确定测头在不同位姿采集的数据之间相对变换关系。

1 摄影测量跟踪系统简介

本文研究的三维扫描测量机器人整体结构示意图如图1所示，机器人本身有6个自由度，扫描测头安装在工业机器人手部，跟踪系统由两个及两个以上高速工业摄像机构成。在扫描测头的4个侧面粘贴有编码标志点，作为摄像机拍摄跟踪测头位姿的显著标志。跟踪系统的每个摄像机可以根据需要安装在合适的位置，保证在测量过程中扫描测头上至少一组编码标志点都可以被至少两个摄像机拍摄到。

在测量过程中，扫描测头由其带动在空间内作旋转和平移运动，扫描测头发出扇形激光束扫描复杂曲面类零部件。任意两个摄像机同步拍摄的图像经由三维重建算法处理，计算出扫描测头在空间中的位置和姿态。采用多相机跟踪系统一方面可以大幅提高测量范围，另一方面也可以降低遮挡问题出现的几率。理论上只要采用足够多的摄像机并且安装位置合理，测量范围可以任意大而且没有遮挡。

图1 整体结构示意图

2 编码标志点设计及其匹配

为了能在图像中提取出足够的、准确的特征点，摄影测量通常要求被测物体表面具有丰富、明显的纹理信息。但是，制造业中的零部件表面通常不满足该条件，而且测量精度要求较高，利用表面纹理提取的特征点无法满足精度要求。这种情况下，只能人为地在被测物体表面粘贴一些标志点，通过快速准确地识别这些标志点，达到获取被测物体表面信息的目的。利用编码标志点可以有效提高识别、匹配速率，便于自动检测[5]。

2.1 编码标志点设计

人工编码标志点的种类很多，一般是根据被测物体的表面情况来选择，而且随着表面的尺寸和复杂度的增加，对编码标志点的数量需求也越大。一般而言，编码标志点有以下几点设计原则：

1)有足够的编码容量。编码容量是指一套编码标志能够包含的唯一编码的个数。

2)唯一性。设计的编码标志点所包含的信息必须具有唯一性。

3)射影变换不变性。拍摄是一个射影变换的过程，经过射影变化后必须仍然具备特定的编码信息。

4)尺寸合适。标志点尺寸如果过大，不仅在布设时容易产生变形，而且会因为成像太大降低识别速率；尺寸过小，成像面积小，编码信息难以识别，而且影响最终的测量精度。

5)易于从背景中分离。图像处理的整个对象包括被测物体、编码标志点和背景。在识别编码标志点时首先要将图像的背景滤除掉，所以标志点要与背景有较大的差别和对比度。

6)编码标志点的设计应尽量简单，以降低处理时间。

在扫描测量机器人应用中，扫描测头跟踪系统必须与扫头同步采样，并且在采样间隔内完成三维重建，对编码标志点识别速度和图像分析处理时间都有非常高的要求，因此应遵循越简单越好的原则。针对这种情况和编码标志点设计的一般原则，本文设计了一种实用的点分布型编码标志点，如图2所示。

图2 编码标志点设计

该编码标志点背景采用黑色，编码标志由最多7个大小相同的高反光圆形标志点组成。编码原理如图2(a)所示，O、C、E、A、B为模板点，定义编码标志的坐标系；M1和M2作为编码点，分别位于直线OCE的两侧，其编码容量为4，满足扫描测头四个侧面的识别定位需要。采用这种方法，可以得到4个编码图案：1)没有编码点M1、M2，定义为图案1，如图2(b)所示；2)只有编码点M1，定义为图案2，如图2(c)所示；3)只有编码点M2，定义为图案3，如图2(d)所示；4)有编码点M1、M2，定义为图案4，如图2(e)所示。

2.2 标志点特征匹配

图像匹配是指将两幅或多幅图像中的同一像素点匹配起来，按照匹配原理可分为基于灰度值的匹配方法和基于特征的匹配方法[6]，本文采用的是基于特征的编码匹配算法。先将图像的背景过滤,利用形态学的腐蚀和膨胀等对图像预处理[7]，使标志点从背景中提取出来并进行中心定位，再利用交比不变性将多幅图像中的编码特征匹配起来。

交比是射影几何学中基本的射影不变量之一。A′、B′、C′、D′为一条直线上的任意四点，A、B、C、D为射影变换后对应的四点，交比不变性如图3所示。

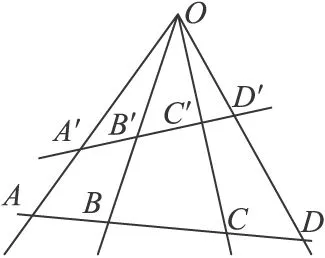
图3 交比不变性

一维交比根据同一直线的四个点的距离来定义，A′、B′、C′、D′的交比为：

(1)

同理A、B、C、D的交比为：

(2)

在射影变换中点列的交比保持不变，即：

R(A′,B′,C′,D′)=R(A,B,C,D)

(3)

对于图2所示编码标志点中的模板点，A、B所在直线与O、C、E所在直线相交得到一个点。根据前述射影几何学原理，该点与O、C、E的交比在不同图像中不变。

利用该性质，提出如下匹配算法。

输入：带有编码标志点图案的图像。

输出：匹配好的同名点。

步骤1 确定初始点集合。给定一个距离因子k，对所有标志点(设其半径为r)逐一搜索其周围k*r内的所有标志点，若找到5个或5个以上标志点，则该标志点连同找到的标志点记为集合G，并继续步骤2；否则继续下一标志点。

步骤2 寻找点O、C、E，在标志点集合G中，搜索共线的三个点，若找到，则位于中间的点确定为点C，否则返回步骤1。由于O、C、E三点排列的方向性，点O和点E存在两种可能性。

步骤3 寻找点A、B，并确定点O和点E。从G中剩余的点中，依据射影变换中交比不变性寻找点A、点B，并根据交比确定点O、点E。位于直线OCE左侧的确定为点A，位于右侧的确定为点B。

步骤4 寻找M1、M2点，并确定编码图案类型。在G中剩余的点中继续搜索，若没有其他的点，则记集合G为图案1。若在直线OCE左侧有一个点，则该点确定为M1，并记为图案2。若在直线OCE右侧有一个点，则该点确定为M2，并记为图案3。若在直线OCE左右两侧分别有一个点，则左侧的点确定为M1，右侧的点确定为M2，并记为图案4。

步骤5 同名点匹配。在多幅图像中重复步骤1～4，并按照编码图案类型和各个标志点编号将同名点匹配起来。

3 关键算法实现

利用图像中的二维信息恢复其在世界坐标系下三维信息的过程称为三维重建。在扫描测头位姿跟踪系统中，经由摄像机同步拍摄的多个图像序列传输到计算机中进行相应的处理：首先，依据编码方法匹配图像中的标志点；然后，利用摄像机的内外参数求出投影矩阵；最终实现标志点的三维定位，得到扫描测头在三维空间中的位置和姿态，达到跟踪定位的目的。

3.1 摄像机模型

数字摄影测量跟踪系统采用摄像机采集图像，其几何基础是针孔成像模型，该模型的特点是来自场景的光线均通过一个投影中心(光心)。如图4所示，主要由光心Oc、光轴和成像平面组成，空间中一点(xm,ym,zm)成像于(u,v)点。

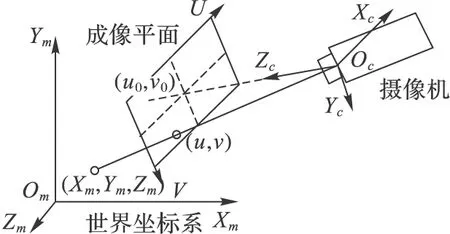
图4 摄像机针孔成像模型

依据摄像机成像原理可以得到从世界坐标系到图像像素坐标系的关系[8]：

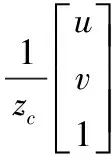
(4)

其中：(u0,v0)为摄像机成像平面中心点的坐标，fu=f/dx，fv=f/dy，f是摄像机的焦距，dx和dy是每个像素在x和y方向的物理尺寸，K为摄像机内参数矩阵，旋转矩阵R和平移矩阵T为摄像机外参数,P为投影矩阵。

3.2 与Kalman预测相结合的CAMShift目标跟踪

CAMShift(Continuously Adaptive Mean-Shift)算法[9]即连续自适应均值漂移(MeanShift)算法，是以MeanShift算法为核心，实现图像任一时刻的MeanShift迭代计算，再以此刻得到的目标窗口为下一时刻MeanShift算法搜索窗口初始值。它相比MeanShift算法的优点是可以自适应跟踪目标远近大小的变化，自动调整搜索框的大小。

为提高目标跟踪速度和降低在复杂环境下追踪伪目标的概率，在CAMShift算法的基础上加入对目标的轨迹预测，就显得很有实际意义和应用价值。

卡尔曼(Kalman)滤波[10]是一种常用的递归滤波器，它能从一组有限的，包含高斯噪声的，对物体位置的记录序列中，预测出物体的位置坐标和速度。它的高效率体现在无需存储大量的历史数据，也可以最大化地利用当前的数据，即通过重复更新系统状态模型，且只为下次更新保存模型。

Kalman预测器状态方程为：

Xk=Ak,k-1Xk-1+Wk-1

(5)

观测方程为：

Zk=HkXk+Vk

(6)

其中：Xk是系统状态向量，Ak,k-1是状态转移矩阵，Wk-1是系统状态的随机干扰向量，Zk是观测系统状态向量，Hk是观测矩阵，Vk是观测噪声向量。

本文基于OpenCV(Open Source Computer Vision)函数库，采用Kalman滤波和CAMShift跟踪相结合的方法，对工业机器人带动扫描测头扫描车门的视频序列进行分析处理，计算出每一帧图像中扫描测头的位置并用白色方框框出，如图5所示，该环节在图像序列中标识出测头完整的运动过程，便于进行后续提取其特征和三维定位等工作。

图5 扫描测头跟踪

3.3 摄像机标定

在进行摄像机定标时，本文采用Zhang[11]提出的平面标定法，该方法对定标板在不同方向多次(三次以上)完整拍照，直接获得相机的内参、畸变系数和外参。该标定方法简单高效，而且克服了传统定标法对设备要求高、操作繁琐等缺点。本文摄像机内参数矩阵采用的是四参数模型：

(7)

3.4 投影矩阵及三维坐标求解

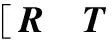
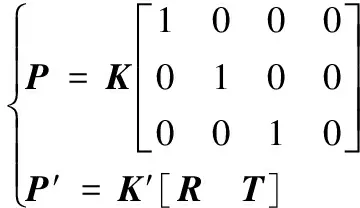
(8)

其中P、P′和K、K′分别为两个摄像机的投影矩阵和内参数矩阵。

令M=(X,Y,Z,1)T是在世界坐标系上的任意一点，M点在两幅图像的成像点分别记为m=(x,y,1)T和m′=(x′,y′,1)T，则在每幅图像中有m=PM，m′=P′M′成立，图像点和三维空间点的投影关系[4]可以表示为：

(9)

其中：piT是矩阵P的i行，X为待求值三维空间坐标。

4 实验及结果分析

为了验证本文的算法，构建了实验系统。在工业机器人手部安装了一个粘贴有四组编码标志点图案的长方体，模拟扫描测头，由机器人带动连续运动。

实验中的摄像机分别在不同的方位采集图像。在一次采样中，第1个相机采集模拟扫描测头图像如图6(a)，由图2可知，原图像中包含图案3和图案4编码标志点。经由背景滤除等图像预处理和标志点中心定位得到处理后的图像，局部放大如图6(b)所示，在高反光标志点的中心标注出了黑色十字。对第2个相机采集的图像进行相同处理，如图7所示。然后通过编码原理将两幅图像中的同名标志点匹配，最终重建出的标志点三维坐标如表1所示，其中O1、C1、E1、A1、B1、M1对应图2(d)的编码图案3所示的标志点，O2、C2、E2、A2、B2，M1′和M2′对应图2(e)的编码图案4所示的标志点。为了更好的可视化效果，基于OpenGL(Open Graphics Library)对重建的标志点进行三维空间显示，渲染效果如图8(a)所示，进一步采用最小二乘法拟合出相应的平面，并依据实物的先验知识重构出模拟扫描测头，如图8(b)所示。

图6 第1幅图像

图7 第2幅图像

表1 编码标志点三维坐标

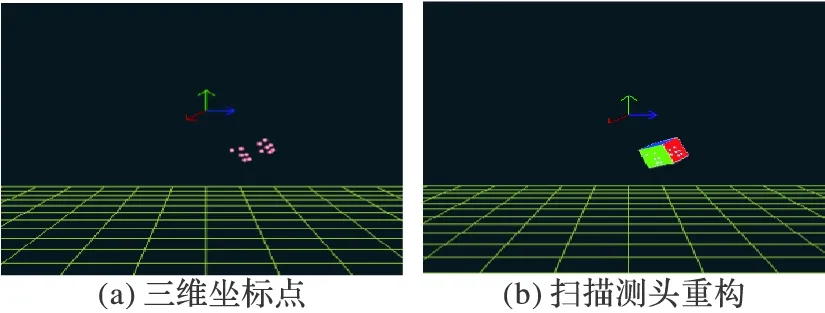
图8 三维重建结果

图9给出了工业机器人带动扫描测头运动过程中9次采样的重建结果，图9(a)为第一次采样的重建结果，图9(b)为9次采样的重建结果，在此基础上得到机器人带动扫描测头的运动路径。通过重建扫描测头在三维空间中的位置和姿态，可以确定测头在不同位姿采集的数据之间相对变换关系。

为了验证三维重建结果的精度，与图10所示的采用德国ACION公司的DPA数字摄影三维测量系统重建的结果进行了分析比较。如表2所示，其中OE1、OE2分别表示编码图案3和图案4中标志点O与标志点E之间的距离，O1O2表示图案3与图案4标志点O之间的距离，d1表示图案3各标志点拟合后平面的平面度误差，d2表示图案4各标志点拟合后平面的平面度误差，angle_12表示图案3和图案4两拟合平面之间的夹角。表2为上述9次采样重建结果和DPA三维测量系统重建结果相关参数的比较。实验结果表明，标志点定位在距离上的平均误差为0.293 mm，在角度上的平均误差为0.136°，算法精度在合理范围之内,验证了摄影测量跟踪系统在三维扫描测量机器人测头定位中应用的可行性。

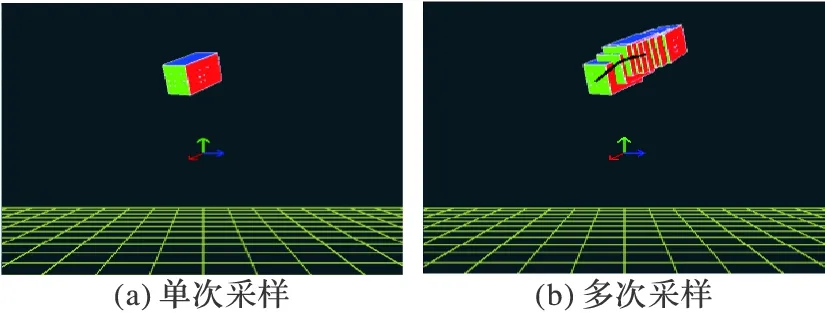
图9 采样重建结果

图10 DPA系统重建结果

表2 三维重建结果误差分析

5 结语

本文提出了一种三维扫描测头精确跟踪定位的摄影测量方法,使得测量精度与工业机器人定位精度无关,可以提高扫描测头的定位精度，从而实现高精度测量。在扫描测量机器人应用中,测头跟踪系统必须与扫描测头同步采样,并且在采样间隔内完成标志点精确识别和三维定位,对编码标志点识别速度和图像分析处理时间都有非常高的要求，针对这种情况和编码标志点设计的一般原则,本文设计了一种实用的点分布型编码标志点,并基于交比不变性提出了相应的编码标志点识别方法。然后利用事先高精度标定过的摄像机的内外参数求出投影矩阵，最终实现标志点三维定位。实验结果表明：多次同步采样重建出的编码标志点三维定位结果误差较小，算法精度满足应用需要。

References)

[1] 王田苗,陶永.我国工业机器人技术现状与产业化发展战略[J].机械工程学报,2014,50(9):1-13.(WANG T M, TAO Y. Research status and industrialization development strategy of Chinese industrial robot [J]. Journal of Mechanical Engineering, 2014, 50(9): 1-13.)

[2] ACERO R, BRAU A, SANTOLARIA J, et al. Verification of an articulated arm coordinate measuring machine using a laser tracker as reference equipment and an indexed metrology platform [J]. Measurement, 2015, 69(1): 52-63.

[3] HARTLEY R, ZISSERMAN A. Multiple View Geometry In Com-puter Vision [M]. 2nd ed. Cambridge: Cambridge University Press, 2003: 239-323.

[4] FAUGERAS O. Three Dimensional Computer Vision [M]. Massachusetts: MIT Press, 1993: 187-205.

[5] 范生宏.工业数字摄影测量中人工标志的研究与应用[D].郑州:信息工程大学,2006:47-52.(FAN S H. Study and application of artificial markers in industrial digital photogrammetry [D]. Zhengzhou: Information Engineering University, 2006: 47-52.)

[6] 贾棋,高新凯,罗钟铉,等.基于几何关系约束的特征点匹配算法[J].计算机辅助设计与图形学学报,2015,27(8):1388-1397.(JIA Q, GAO X K, LUO Z X, et al. Feature points matching based on geometric constraints [J]. Journal of Computer-Aided Design & Computer Graphics, 2015, 27(8): 1388-1397.)

[7] 徐志平,钟亦平,张世永.基于交叉视觉皮质模型二值图像形态学算法[J].计算机辅助设计与图形学学报,2007,19(8):991-994.(XU Z P, ZHONG Y P, ZHANG S Y. A binary image morphological processing algorithm based on intersecting cortical model [J]. Journal of Computer-Aided Design & Computer Graphics, 2007, 19(8): 991-994.)

[8] 佘彦杰.基于多幅图像序列的三维重建[D].长春:吉林大学,2006:15-18.(SHE Y J. 3D reconstruction based on image sequences [D]. Changchun: Jilin University, 2006: 15-18.)

[9] 王晋疆,刘阳,吴明云.基于快速鲁棒特征的CAMShift跟踪算法[J].计算机应用,2013,33(2):499-502.(WANG J J, LIU Y, WU M Y. CAMShift tracking algorithm based on speed-up robust features [J]. Journal of Computer Applications, 2013, 33(2): 499-502.)

[10] 权义萍,金鑫,张蕾,等.基于Mean-Shift的卡尔曼粒子滤波车辆跟踪算法研究[J].计算机应用与软件,2014(9):236-239.(QUAN Y P, JIN X, ZHANG L, et al. On vehicle tracking algorithm using Mean-Shift-based Kalman particle filter [J]. Computer Applications and Software, 2014(9): 236-239.)

[11] ZHANG Z. A flexible new technique for camera calibration [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334.

[12] PAZOS S, HURTADO M, MURAVCHIK C H, et al. Projection matrix optimization for sparse signals in structured noise [J]. IEEE Transactions on Signal Processing, 2015, 63(15): 3902-3913.

This work is partially supported by the Independent Innovation Fund Project of Anhui Province (JZ2015QSJH0244), the Foshan Science and Technology Innovation Special Fund Project (2014IT100115).

LIUHong, born in 1993, M. S. candidate. Her research interests include machine vision, photogrammetry, image processing.

WANGWenxiang, born in 1993, M. S. candidate. His research interests include machine vision, photogrammetry.

LIWeishi, born in 1970, Ph. D., professor. His research interests include reverse engineering of complex shape detection, computer aided geometric design.

Photogrammetricmethodforaccuratetrackingof3Dscanningprobe

LIU Hong*, WANG Wenxiang, LI Weishi

(SchoolofInstrumentScienceandOpto-ElectronicsEngineering,HefeiUniversityofTechnology,HefeiAnhui230009,China)

For the traditional 3D robot scanners, the measuring precision is dependent on the positioning precision of the robot, and it is difficult to achieve high measuring precision. A photogrammetric method was proposed to track and position the 3D scanning probe accurately. First, a probe tracking system consisting of multiple industrial cameras was set up, and coded markers were pasted on the probe. Then, the camera was calibrated with high precision and interior and exterior parameters of the camera were obtained. Second, all cameras were synchronized, the markers in the image were matched according to the coding principle, and the projection matrix was obtained. Finally, the 3D coordinates of the markers in space were computed to track and position the probe. The experimental results show that the mean error of the marker position is 0.293 mm, the average angle error is 0.136°, and the accuracy of the algorithm is within reasonable range. The photogrammetric method can improve the positioning precision of the probe, so as to achieve high precision measurement.

industrial robot; 3D scanning probe; coded marker; photogrammetry; tracking

TP242.6; TP391.413

:A

2017- 01- 05;

:2015- 02- 24。

安徽省自主创新资金资助项目(JZ2015QSJH0244)；佛山市科技创新专项资金资助项目(2014IT100115)。

刘虹(1993—)，女，安徽淮北人，硕士研究生，主要研究方向：机器视觉、摄影测量、图像处理； 王文祥(1993—)，男，江苏泗洪人，硕士研究生，主要研究方向：机器视觉、摄影测量； 李维诗(1970—)，男，山东蓬莱人，教授，博士，主要研究方向：复杂外形检测反求工程、计算机辅助几何设计。

1001- 9081(2017)07- 2057- 05

10.11772/j.issn.1001- 9081.2017.07.2057