基于深度学习的航空器异常飞行状态识别

吴 奇 储银雪 /

(上海交通大学，上海 200240)

基于深度学习的航空器异常飞行状态识别

吴 奇 储银雪 /

(上海交通大学，上海 200240)

飞行设备快速存取记录仪(Quick Access Recorder, 以下简称QAR)保留了原始航班各类重要飞行参数在内的航行信息，使研究分析航空器实时状况和保障飞行质量成为可能。针对QAR数据高维大样本的特点，在如今大数据背景下，除了传统机理建模分析航空器飞行状态外，采用深度学习的方式建立基于数据驱动的航空器飞行状态识别模型，理论与实用意义兼具。通过对真实QAR飞行数据的研究，开发了基于深度稀疏受限玻尔兹曼机的异常飞行状态识别程序。首先利用小波降噪技术对原始飞行数据进行预处理清洗，在一系列典型飞行参数上提取经典时域特征以及小波奇异熵等信息熵特征构成特征集。在此基础上，分别利用经典的线性主元分析技术和深度稀疏玻尔兹曼机对特征集进行有效降维，最后采用四折交叉验证方式，通过高斯过程分类器实现对飞行状态的辨识。实验结果显示，基于深度受限玻尔兹曼机-高斯过程分类的飞行状态识别具有较高分类准确性。

飞行状态识别；深度学习；高斯过程

0 引言

1903年，飞机的问世，为人类开辟了陆地、海洋之外的新边疆。由此衍生出来的各类航空器除了作为交通工具极大便利了人们的出行外，还发挥了军用、民用、商用等诸多用途。航空器大规模宽领域的普及应用，随之而来的最重要问题便是安全，其中最关键的考量当属如何确保航空器飞行状态安全可控(新近事故如2014年3月马航MH370客机失联，至今仍是未解之谜)。为此，分析和研究航空器飞行状况的辨认意义重大：不仅是航空器飞行状态分析的必要基础，更能为繁忙空域多机(群)任务调度与目标规划、智能故障诊断和维修维护等安全监控，以及航空器设计优化与成本控制等方面提供重要有效的参考信息。

可行性上，航空器飞行状态的识别目前大体有三种路径：基于分解重构的机理建模，其辨识效果与模型准确性严格正相关；基于知识经验库的专家系统，即便综合主客观分析，其不足在于领域专业性与人为主观判定的局限性；本课题采用第三种路径，即基于数据驱动的信号处理方法，运用真实飞行数据进行机器自学习，进而捕捉挖掘样本数据内在特征与飞行状态之间的关联，兼具理论与实用意义。

首先在理论研究价值上，研究大数据云计算背景下基于数据挖掘驱动的航空器飞行状态识别，将打破传统机理建模和经验知识结合主观判定分析飞行事件的套路，有助于建立并完善着眼全流程各环节的飞行数据分析与结果导向型飞行安全控制融合的研究体系。另一方面，也将助推理论研究从事后故障诊断研究向超前预防型预警风控研究发展，从而更有效确保航空器飞行状态的安全可控。

其次在应用层面，通过深挖捕捉海量飞行数据样本潜在的特征因子，进而用于识别飞行过程的异常状态，预防或减少环境因子或人为因子导致的不安全隐患，等效达到了安全保障层前置和有效风险防范的目标；进一步，基于真实飞行数据在线分析平台的状况评估体系，呈现了航空器包括气候状况、飞行姿态等多维度全方位的情形再现，进一步可用于地面实时快速掌握航空器飞行状态，并在必要时为空中机组提供有力支援，从而最大限度地减少可能发生的损失。

1 国内外研究现状

国内外关于航空器飞行状态的研究，大体可划分为两大经典模式：一是借由滤波分析模型递推计算出航空器运动学方程；二是示教训练方式，经由对历史航班相关特征参数信息的训练学习，形成空管领域的专家经验[1]。

1.1 国外飞行状态识别研究现状

国外的研究在滤波模型和机器学习两方面均有涉足。Inseok Hwang等人基于滤波模型设计混合模型预测航空器飞行状态，采用卡尔曼滤波减小了因错误预测引入的误差，进而更有效地捕捉了短时飞行特征[2]。Neogi等人使用隐马尔科夫模型研究航空器飞行状态的变化，结合随机混合系统探测飞行状态的变化，考虑 了随机扰动的影响[3-4]。还有学者采用Swarm模型，引入人工智能模拟类似动物的群体效应，用以形成冲突解脱方案[5-6]。2012年，WANG Qing等人基于QAR(Quick Accesses Recorder)数据，提出了EKF-MBF(the Extended Kalman Filterassociated with Modified Bryson-Fraziersmoother)混合算法，改善了相关估计指标精度[7]。C. EdwardLana等人则采用QAR数据分析了高纬度机场降落时的飞行特征，为潜在安全问题提供分析帮助[8]。B.Jia等人引入BF-PSO(Bacterial Foraging-Particle Swarm Optimization)算法来优化KFCM的参数已达到辨识动态与静态模式下的飞行状态[9]。

1.2 国内飞行状态识别研究现状

国内学者则主要在滤波分析模型聚焦较多且通常结合了空管的专家经验[10]。张友民等学者为估计高维航空器姿态，采取了非线性滤波模型[11]。耿建中等为确保准确可靠辨识航空器状况的同时降低运行成本，引入了无迹卡尔曼滤波(Unscented Kalman Filterm)的滤波方法。高原等专门针对飞行状况规则辨认与提取的课题，以典型参数为研究对象，提出新型量子遗传算法以期组合寻优，归纳了飞行状况识别的所谓产生式法则[12]。2013年，王洁宁等将终端区数据一致化，并利用历史航行信息特征训练隐马尔科夫模型，搭建了时序辨认模型[13]。2015年，李军亮等人预先将对待识别的飞行状态经由Elman网络预先分类，在某款直升机的辨识应用中取得成功[14]。2016年，熊邦书等人提出基于支持向量机(Support Vector Machine,SVM)的直升机飞行状态辨认方法，在数据集较少情况下明显提升了分类正确率[15]。赵元棣、孙禾为准确高效预测航空器飞行状态，提出了HMM-BP混合模型，通过HMM模型对航空器进行时序建模，再利用BP神经网络对航空器飞行状态进行推理预测，计算快效率高[16]。谷润平等选用新型数据融合算法和扩展卡尔曼滤波算法分析飞行参数，提高了判别预测的准确度[17]。

2 特征提取技术

航空器飞行状态的识别，是一类典型的模式识别问题，核心在于透过元始一般性的数据信号，发掘其内在独特的关联，从而将一般的飞行信号转化为可识别的有特征信号。在完成前述对一手数据降噪处理后，紧接着的难题便是对特征的表示与提取，试图将原先隶属于相异类别的典型参数进行提取后转化为或有物理解释意义或有识别意义的数据，更好地强化表征航空器所处的状况。特征工程的方式层出不穷，经典手段诸如均值、方差和均方根，在展示信号(也适用时间序列)的幅值特征及不同类别参数的差异性，已由早期统计学应用推广到各类数据分析领域。然而，仅仅使用传统时域的特征分析技术已无法为高维度强耦合的繁杂飞行数据分析提供强有力支撑，难以准确应对非线性或非平稳的信号特征。为满足人们对更高识别准确率的迫切现实需求，发展运用新的特征提取技术是一大广阔的舞台。本节除简介经典时域内特征提取技术外，还将熵量特征融合信号变换技术创新特征工程，引入自回归滑动平均系数熵(ARMAE)及小波奇异熵(WSE)，以构建更精确反映原始数据潜在关联的特征集。

2.1 时域特征提取技术

特征是任何学习型算法的原材料。本小节引入三个常用的时域的统计特征量：均值(mean)、方差(variance/deviation)、均方根值(RMS, root means quare)。

对于时间序列进行一维数据分析时，均值是最常用以描述飞行数据的特征量。这里均值不是几何平均值，指的是算数平均值，计算方法见式(1)(xi为样本内数据值，Pxi为xi出现的几率),常用以表征原始波形的幅值特征。若将原始信号视作不同频率信号之叠加，此时，均值的物理意义表现为信号中直流分量的大小。

进一步，为了反映原始全体单个样本与均值的关系(离散程度)，引入方差(用variance或deviation表示)，计算方法见式(2)(其中，xi为样本内数据值，Pxi为xi出现的几率)。由公式易知，方差是一个离差量，描述的是时间序列的波动范围，而且是基于均值的分散特征：计算时扣除了均值这一表征直流分量的参考基准，故方差大小又表征了信号交流分量的强弱，也即交流信号的平均功率。

融合考虑交直流分量的功率，我们还可以引进均方根值，用RMS(Root Mean Square)表示，计算公式见(3)，也称有效值。均方根的平方即均方值，物理意义为信号的平均功率，这里的平均功率即信号的直流分量功率与交流分量功率之和。

2.2 自回归滑动平均熵

本小节从时域内的自回归滑动平均模型出发，引入熵概念，定义自回归滑动平均熵，用以衡量反映飞行数据的信息量及体现原始信号在时间维度上的随机不确定性。

从理论视角来看，自回归滑动平均模型(Auto-Regressiveand Moving Average Model, 简称ARMA)集自回归模型(AR)和滑动平均模型(MA)之大成，是以待定系数标准模型应对随机过程的经典手段：将输入信号视为随机变量，从而，信号在时间维度上的延展反映为随机变量所具有的依存关系。该模型是差分多项式混合模型，综合考虑受因素演化的联动影响效应和自身变动规律的影响效应，可用于消除序列的线性依赖从而去除序列的自相关性；同时也是长期追踪历史资料并加以回归预测的利器，如可用于国家或省级内城乡居民的收入差距预测的研究、用于市场规模及销量预测的零售消费业研究，等等。

我们在自动控制原理里学习过，一个零均值的平稳序列，其在外界激励下的响应(在t时刻记为Xt)不仅与当前和过往的响应值相关，还与激励前外在的扰动值密切联系，满足这样规律的可称之为自回归移动平均系统。在数学意义上建模即称样本集在时间维度上服从(p,q)阶自回归滑动平均混合模型，记为ARMA(p,q)：

其中，{at}为白噪声序列。特别地，p=0时模型退化为MA(q)；q=0时模型即为AR(p)。

由上述公式易知：定阶，即确定上述p,q值，是搭建自回归滑动平均模型成功与否的关键。基本思想容易理解，通过逐步增加p,q值直到阶数增加而残差平方和无法明显下降为止。本文采用先预估(p,q)范围，而后通过模型拟合度量AIC极小准则来定阶。AIC[18]计算公式如(5)所示，V为模型残差方差，N为序列的长度。

经由上述步骤，ARMA模型参数业已确定，容易发现，应用于高维的飞行参数数据集时，各参数在时间维度上适用的ARMA模型系数的长度不同，不便于后续特征处理；同时，仪表盘参数在时间维度上呈现出的复杂性某种意义上可用随机程度加以描述，因为序列增长随之衍生出新序列，这种模式的演化正是系统复杂性的反映。能否考虑变化混乱度的因素呢？很幸运，可以用德国热力学家R.Clausius提出的熵(Entropy)评价。回溯科学发展史，熵概念的问世，不仅标志着衡量系统复杂度的全新思路诞生，更是有广阔里程碑意义的：早已延拓至热力学外的信息学、数理应用和生命科学等领域。譬如，1948年Shannon第一次给出信息模型的信息熵，定量地解读了信息这个抽象的观点。本文使用的自回归滑动平均熵(Auto Regressive Moving Average Entropy, ARMAE)源自于自回归滑动平均模型[19]，计算方式如下：

如此一来，借由通信原理的信息熵的思路：信息量大小反映于基本信息符号重复出现频次的概率，结合消除序列自相关性的自回归滑动平均模型，定义的体现飞行参数随机不确定性的复合熵量ARMAE，将为后续的飞行状态识别提供更坚实可靠的保障。

2.3 小波奇异熵

前述的特征提取着眼于人们日常习惯的时域，然而，频域分析是上世纪以来信号分析更为主流的分析方法，如傅里叶变换。不过，该方法也几乎全然摒弃了时域的信息。于是，由傅里叶分析衍生进化出的小波分析，成为了具备优良时频局部化性能的时-频分析新方法。本小节将描述序列混乱度的奇异熵集成小波分析思想，引入小波奇异熵(Wavelet Singular Entropy, 简称WSE)刻画非线性强噪声奇异能量分散的统计特征，以综合更多动态特征提高对噪声的免疫力及状态识别的准确率。

小波变换的原理方法已在2.1节提及，此处不做赘述。降噪飞行数据经小波变换后再经由内积公式即可得到小波系数阵A，从而在多频率多尺度下分解原始信息为主要逼近分量和细节微调分量，等效于反复组合运用高低通滤波器，兼备了单一时域或频域分析法的优势。

数学的美在于简洁，时频的直观分布还不够，大数据量属性是准确进行模式识别的掣肘。线性代数中的奇异值分解理论，能将秩为k的任何阶次的矩阵A按奇异值分解为k个单秩子阵的加总(详见公式(8))，达到特征值对角化呈现之效用，这样一来，奇异对角阵实质上表征了待分解阵A的最小模态特征。

其中，U、VT均为正交矩阵，Λ上对角元素λi(i=1,2,…,r)即为A阵的奇异特征值。

小波系数阵A通过SVD[24]分解后所得的对角阵，简洁地刻画了飞行数据的时频分布特性。为进一步度量分布的混乱程度，结合2.2节的介绍，将奇异特征值用熵进行表示。奇异熵事实上是一种信息熵。我们知道，香农信息熵理论奠定了通信原理的基石。通俗地借由生物学概念不难理解，在基本信息要素构成的生态系统中，基本信息越多越难以加以定性，因为其出现的频次不会完全一致，即出现了混乱随机性；由此出发，以概率视角刻画这种随机不确定性便十分自然了：考虑小波变换后系数阵A的奇异值，依信息熵原理计量得小波奇异熵如下，参数k表示非零特征值的数目。

综上，小波奇异熵的计算过程如图1所示。

3 深度稀疏受限玻尔兹曼机网络

3.1 深度置信网络

与传统(以主元分析为经典)样本数据特征分析程式相比，深度置信网络是个概率发生器，不具备一般人工特征提取时不可避免的主观不确定性，降低了对专家系统或称经验知识的密切依赖从而具备自动提取信号特征的自适应性；此外，该模型非常适合非线性非低维的飞行数据处理，这在后续的实验验证中可以得到完美体现。DBN模型由单层反向传播网络(BP，Back-propagation)和几层限制玻尔兹曼机(RBM)构成[25]，结构如图2所示。

深度置信网络的模型搭建过程主要分为两大块：其一是训练若干层的RBM，采用无监督的方式，从而保证特征向量向其他空间投射时仍能保留尽可能多的能量[25]；其二就是有监督地借由顶层的反向传播网络训练优化网络全局，从而微调网络模型以获取深度置信网络的最优参数。

由上面的介绍，不难获知：受限玻尔兹曼机(RBM)是DBN中的关键基本环节。作为玻尔兹曼机的一种特殊形式[26]，受限玻尔兹曼机由可视层和隐含层构成，底层靠n个可视节点排列而成，顶层由m个不可见节点堆成故称为隐含层并用以提取特征。受限玻尔兹曼机的网络结构可用图3展示。

定义受限玻尔兹曼机的网络能量可用下式：

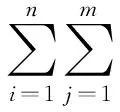
其中，b=(b1,b2,…,bn)表征的是底层可视节点的转移量，c=(c1,c2,…,cm)表示隐含层的隐藏节点偏移量，wn×m则是沟通隐含节点与可视节点的权重矩阵。

采用概率发生的方式有效防止了人为主观臆断。受限玻尔兹曼机网络实质上是几率模型：对于输入数据v=(v1,v2,…,vn)，RBM网络充当了中继处理再生器，输出对应的隐含特征向量h=(h1,h2,…,hm)，从而使得联合概率p(v,h)极大化。其中，p(v,h)满足式(13)。

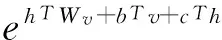
进一步详解：可视意即一个观察入口，从已知的底层可视节点获取隐含层的节点值，有公式(14)作为桥梁；为达到不断优化不断微调，没有反馈不行，即上述的逆向操作也需要可行：由已知的顶层节点亦可获取底层可视节点的值，公式见(15)。

如前所述，深度置信网络是将若干层受限玻尔兹曼机预训练的模型结合反向传播网络监督下进行微调的网络模型，从而提高全模型的计算性能。以下将整套模型的实施步骤分为预训练环节和微调环节叙述。

首先，预训练环节指的是无监督式地自下而上的采用若干层RBM自训练方法获取稳定的网络结构。这一模型参数的获取可借由极大化RBM网络训练集的对数似然函数获取，见式(16)。

对训练样本运用Gibbs采样，可有下面的对数似然的梯度近似表达式。

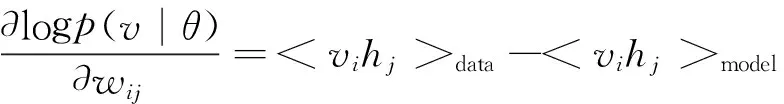
不过针对飞行数据这样的高维数据时，Gibbs采样次数过多使得整个训练过程效率难以接受，需要保证计算精度的情况下提高计算速度。Hinton于2002年创立的对比散度(Contrastive Divergence, CD)是一种快速学习方法：通过CD法仅需k步(通常情况下仅需一步)，下面展示了其参数的更新公式。

其中，ε是学习速率，<>recon为样本分布的期望。

现在介绍微调阶段。作为一个有监督的分类器，反向传播网络(BP)在整套深度置信网络中起着微调全体结构从而达到全局最优的作用。这一细调过程依靠的是误差信号的逆传播以调整若干层前馈环节。训练数据逐层传播到顶层获取输出过程中，每个神经元均有一个激活函数，通常为非线性的sigmoid函数：

其中，xi称为神经元i的激活值，yi即为输出。

将网络输出值与标准值作差即得误差信号，再将这一反馈信号从输出层向输入层逐层传播以对网络参数寻优即可。

3.2 稀疏受限玻尔兹曼机

生物医学的临床研究成果启发我们：人脑处置信息的过程并不是满仓全负荷行为，通常仅少数的神经元被激发。这一规律被称为稀疏编码的算法用以模拟大脑编码历程[27]。那么，仍然从概率视角，限制整套网络的激活概率能否提高网络对噪声干扰的鲁棒性呢？经过稀疏受限玻尔兹曼机(SRBM)即可。

需要首先说明的是，由于本文实验测试采用的是真实飞行数据，可视层输入必须是真实数据不是布尔型二值数据，故应建立高斯受限玻尔兹曼机模型[28]，此时确定状态下RBM网络的能量定义为：

上式中的参量与前面RBM能量式的定义相同，σ在实际应用中设定为1较常见[28]。以此类推，我们仍然可以搭建可见层节点与隐含层节点的桥梁：

此时，数值上，隐含节点表现为稀疏性，故而还得在目标函数上叠加一个正则化项以确保隐含节点数值维持低激活率。具体说来，对于拥有m个样本的数组{v(1),…,v(m)}，优化目标见式子(27)。

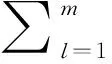
其中，λ表示正则化常数，隐含节点的稀疏性由稀疏常数p把关控制。

这样一来，经过预训练过程后，得到的便是SRBM参数的值，再通过类似标准深度置信网络模型的微调技术手段，便可有效获取SRBM模型的最优参数，从而学习到不同类别的特征差异。下一部分，将结合实际应用展示SRBM的强大功能。

4 基于高斯过程的飞行状态识别

定义一个二分类问题，首先训练集{(xi,yi)|i=1,…,m}，xi为输入向量，X=[x1,…,xm]T，yi∈{-1,+1}，yi表示两种输出标签的类别。已知训练集，则测试集x*属于+1类的概率可表示为：

其中σ(z)=1/(1+e^(-z))，易知此函数范围为(0,1)；一般当π(x)>0.5，可认为测试样本x*属于+1类，否则应划分至另一类。当测试样本x*为待预测样本时，预测一般分两步：计算f(x*)的分布及其概率预测值：

以上两式计算前提在于似然函数是高斯函数，也就要求在回归情况下方可行。当分类问题中，似然函数并非高斯函数，上述两式不能精确计算，只能近似这两个积分，这时我们可用高斯分布近似f*的后验分布：

上式的均值、方差如下(式中，k*=[k(x*,x*),…,k(xm,x*)T为测试集的数据与训练集的数据的协方差)

这样一来，便可用近似解分析非高斯分布以最佳近似高斯分布，即对于测试集而言，其高斯预测概率值的解可表示为：

至此我们基本阐释了高斯过程分类的基本原理，下一小节希望将其应用到前述降维后的典型飞行参数的特征集中，以完成航空器飞行状态模型的建立与测试。

5 实验

5.1 实验数据

自1997年起，中国民航总局(CAAC)依据中国民航适航指令要求所有国内运输类飞机强制安装飞行设备记录仪器(Quick Access Recorder,简称QAR)。也正是因为QAR记录着航班包括飞行位置、操作控制等诸多性能方面的信息，分析研究QAR数据将有助于提高飞行安全和监测飞行品质。然而对于各大航空运输公司而言，QAR飞行数据属于核心商业机密，故无论国内还是国外，基于QAR飞行数据的研究相对较少。本论文实验数据源于国家级基金项目，实验数据为真实飞行数据，是同一家航空公司同一机型(波音747)的同一航线(浦东-白云)的两次不同天气状况(能见度差异较大)的QAR飞行数据。选取的飞行任务为飞行中最危险也即事故发生率最高的进近着陆阶段[20]，每组数据共3 000个样本点。验证平台选取64位Windows10操作系统，并利用编程软件MatlabR2014a搭建实验环境，如图4所示。

考虑到最终搭建的飞行状态识别不仅限于分析还要能进一步用于实时恶劣状态预警，因此模型判断时间应尽可能缩短，故本文选取最能反映航空器飞行姿态的典型飞行参数[21]进行特征提取并建模，初始的典型飞参集列表详见表1。接下来，本文将运用数据挖掘即机器学习的手段通过QAR数据搭建航空器飞行状态的识别流程。

5.2 典型飞参特征集的降维

5.2.1主元分析线性降维

在5.1节我们完成了面向典型飞参的特征集构建，本小节中我们利用本文前述的理论知识，将主元分析法应用于典型飞参特征集的降维。如前所述，PCA主要流程为将中心化后的样本求取其协方差，获得降维矩阵后映射即得降维数据。这里，我们为了直观展示降维后效果，利用主元分析将5.1节中得到的包含时域、ARMAE、WSE特征在内的120×72维典型飞参特征集(两种天气状态下共计120组，每组72维特征)，降维到3维空间使其可视化。

表1 建模所选取的典型飞行参数集

由图5可见，对于典型飞行参数特征集通过PCA降至3维后，其特征点散落在三维空间各处；两种相异天气状态类别的特征点互相交织，很多无法划分。由于PCA是线性降维算法，虽对于原始信号一定程度上保留了更多能量却无法提取非线性的重要特征。为此，我们接下来看看非线性数据降维算法SRBM处理的效果。

5.2.2稀疏受限玻尔兹曼机降维

如前所述，QAR数据属于各大航空公司的商业数据，由于数据来源的限制，无法获取非常多的样本训练模型，因此除了需要尽量减小噪声对模型的干扰影响，还需要防止模型学习中容易发生的过拟合情况。本文前面几节专门叙述了SRBM在这方面的强大优势：透过限制玻尔兹曼机(RBM)模型正则化隐含层里的隐藏点，便可有效对隐藏点概率加以限制从而达到稀疏的目的。下面将运用SRBM算法对5.1节得到的典型飞参特征集作降维。由于QAR记录的参数是真实的航行状态，故不必对真实数据作二值化的脱敏处理，但要在降维前对典型飞参特征集的样本作规范化处理。

所谓归一化，即将待处理数据限制在拟定的范围内，比如将样本特征归一化到[0,1]间，表征其在统计意义上的概率分布。这样做的好处在于，一方面便于后续数据处理使本不具备可比性的数据具备相对可比性，同时由于是等比例缩放，也保留了原数据间相对大小关系；另一方面当然也提升算法收敛速度以更好满足实时要求，因为这样处理避免了数值计算中的复杂度。本节采用的归一化包含样本中心化和去量纲处理两步(需要说明的是，Matlab中仅使用自带normalize函数即可完成归一化操作)。

首先是数值中心化，即使数据集的均值归零以便于后续降维算法处理：

第二步便是去量纲，即将数据的方差切换为1，公式如下：

与PCA降维输入的样本数据相同，我们已提取时域、ARMAE、WSE等特征在内的典型飞参特征集，共计正常天气状态60×72维特征集数据、异常天气状态60×72维特征集数据。完成前述归一化操作后，第二步就是设定SRBM的参数，此处初始化SRBM网络选择以正态随机分布，阈值初始化为0；最大迭代次数设定为100；sparsity Variance设定为0.1；稀疏度sparsity Target设定为0.02；稀疏代价sparsity Cost设定为3；参数表现模式选择为“reconstruction”。最后，整套网络通过将SRBM结构与反向传播网络BP相结合从而达成有监督降维，提高了网络的全局性能。这是由于SRBM网络学到的为一般化普适的概念化特征，仅能保障各层内特征映射局部最优却不能整体最优，因此在顶层引入BP有监督训练整个网络，可将误差信息反馈给SRBM层从而细调整个网络的模型参数以达成不同类别天气状态的特征数据降维的差异化。使用BP网络在matlab中只需要调用自带的backpropagation函数即可。

考虑到输入特征的维数，本文SRBM选择3层较为适宜，即从72维先降维到30维，再降维到3维即可可视化通过SRBM降至3维的典型飞行参数特征集，如图6所示。

由图6可见，总体而言，SRBM降维得到的不同类别的典型飞参3维特征可较有效地达成一定程度的聚合，尽管仍有少量不同类别的特征点出现了重合，但相比线性PCA降维而言，降维效果获得了较大的提升。下一节将进一步通过机器学习分类器的方法展示该降维提取特征对于飞行状态识别的有效性。

5.3 基于DSRBM-GP的航空器飞行状态识别

本研究的目标是利用机器学习的方式建立航空器的飞行状况辨认识别模型，是一类典型的模式识别问题，涵盖原始预处理的数据清洗、特征提取的特征工程、特征降维和建立分类器一系列流程。依据前述的高斯分类器原理，可以建立如下的基于高斯过程分类的飞行状态识别模型。

第一步，分别从经过PCA和SRBM降维后的特征集中选择适量的样本(训练集大小后文交叉验证时说明)作为高斯分类器的训练输入。依据本文前述理论，将标记为正常天气状态(y=+1)的特征集作为一类，标记为异常天气状态(y=-1)的特征集作为另一类，初始化协方差矩阵，利用拉普拉斯近似法获取协方差函数的最后超参数hyp1；

第二步，将待预测判定的样本数据输入对应于hyp1的高斯过程分类器，并依据式(29)获取预测样本数据划分为+1类的预测概率。此时，若预测概率值大于0.5,则认定该样本所属的飞行天气状态为正常；否则，认定所处的天气状态为糟糕。

为了验证所建立的飞行状态识别模型，需要将上述预测判定的类别与实际标签比对从而确定模型的识别准确率。本研究的问题是二分类问题，容易定义识别准确率公式如下：

为对比经PCA降维和SRBM降维后分类的效果，本文采用4折交叉验证，即将经特征降维后的全体特征集样本数据随机等分成4组，其中3组作为模型的训练集训练基于高斯过程的状态识别模型以确定高斯核参数，剩下1组作为测试集检验识别模型准确率；最后对4次交叉验证的准确率取平均值，更能代表该模型的准确性。图7展示了两种降维算法在高斯过程分类下的四折交叉验证结果，其中SRBM-GP分类准确率高达83.33%，而PCA-GP分类准确率仅为62.5%，容易得知经过SRBM降维提取的三维特征拥有较高的分类正确率。

进一步，为了更直观展示经过两种降维算法降维后在高斯过程分类器下的分类结果，借助两种降维模型提取有效两维特征输入高斯过程分类器，可在二维等高斯概率线上展现各个测试点的分类结果。如图8～9所示，容易更直观地比对出：SRBM-GP算法的分类效果是远高于PCA-GP算法的，与上面的交叉验证结果相符，验证了本文提出算法的有效性。

6 结论

本文围绕航空器飞行状态识别的目标建立了基于高斯过程分类器的识别算法。为验证模型有效性，本文考虑到样本数量，采用了四折交叉验证取平均值作为模型分类正确性的标准，并将分类结果进一步作了二维可视化呈现，比对了经过主元分析和稀疏受限玻尔兹曼机降维后的特征，从而验证了本文提出的基于深度稀疏玻尔兹曼机降维算法在高斯过程分类器下的分类正确性。

[1] 孙禾.航空器飞行状态预测方法研究[D].天津：中国民航大学,2014.

[2] Inseok Hwang, Jesse Hwang, Claire Tomlin. Flight-Mode-Based Aircraft Conflict Detection using a Residual-Mean Interacting Multiple Model Algorithm[C]// AIAA Guidance, Navigation and Control Conference and Exhibit, August 11-14, 2003.

[3] Natasha A. Neogi, Asal Naseri. Using hidden markov models to detect mode changes in aircraft flight data for conflict resolution[C]// IEEE International Conference on Systems, Man, and Cybernetics, Taipei, Taiwan, October 8-11, 2006.

[4] Asal Naseri, Natasha A. Neogi. Stochastic hybrid models with applications to air traffic management[C]// AIAA Guidance, Navigation and Control Conference and Exhibit, August 20-23, 2007.

[5] E.Ronchieri,L.Pollini,M. Innocenti. Decentralized Control of a Swarm of Unmanned Aerial Vehicles[C]// AIAA Guidance, Navigation, and Control Conference and Exhibit, South Carolina, August 20-23, 2007.

[6] Erik de Vries, Kamesh Subbarao. Cooperative Control of Swarms of Unmanned Aerial Vehicles[C]// 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Florida, January 4-7, 2011.

[7] Qing WANG, Kaiyuan WU, Tianjiao ZHANG, Yi’nan KONG, Weiqi QIAN. Aerodynamic Modeling and Parameter Estimation from QAR Data of an Airplane Approaching a High-altitude Airport[J].Chinese Journal of Aeronautics. 2012, 25(3): 361-371.

[8] C. Edward LAN, Kaiyuan WU, Jiang YU. Flight Characteristics Analysis Based on QAR Data of a Jet Transport During Landing at a High-altitude Airport[J]. Chinese Journal of Aeronautics. 2012, 25(1): 13-24.

[9] B. Jia, C.F. Wei, J.F. Mao, R. Law, S. Fu, Q. Wu. Identification of flight state under different simulator modes using improved diffusion maps[J]. Optik—International Journal for Light and Electron Optics. 2016, 127(9): 3905-3911.

[10] 耿建中,姚海林.基于UKF的飞机飞行状态估计[J]. 系统仿真技术及其应用, 2008, 10: 56-59.

[11] 张友民,张洪才,戴冠中等.非线性滤波方法及其在飞行状态及参数估计中的应用[J]. 航空学报. 1994, 15(05): 620-626.

[12] 高原,倪世宏,王彦鸿等.一种基于改进量子遗传算法的飞行状态规则提取方法[J]. 电光与控制, 2011, 18(1): 28-31.

[13] 王洁宁,孙禾,赵元棣. 面向终端区航空器飞行状态识别的HMM方法[J]. 航空计算技术,2013,02:1-5.

[14] 李军亮,胡国才,韩维,柳文林.基于Elman网络的某型直升机飞行状态识别[J]. 火力与指挥控制,2015,12:57-60.

[15] 刘雨. 基于SVM的直升机飞行状态识别方法及其应用研究[D].南昌：南昌航空大学,2016.

[16] 赵元棣,孙禾. 航空器飞行状态预测的混合模型研究[J].飞行力学,2016,04:81-85+89.

[17] 谷润平,黄磊,赵向领. QAR数据的数据融合算法[J]. 计算机系统应用,2016,01:136-140.

[18] H Bozdogan. Model selection and Akaike’s information criterion (AIC): The general theory and its analytical extensions[J]. Psychometrika.1987, 52(3), 345-370.

[19] Box,G.E., Jenkins,G.M., Reinsel,G.C. Time series analysis: forecasting and control[M]. John Wiley & Sons, 2011.

[20] Verwey W B, Veltman H A, Detecting short periods of elevated workload: A comparison of nine workload assessment techniques[J]. Journal of experiment psychology, 1996, 2(3), pp 270-285.

[21] B. Jia, C.F. Wei, J.F. Mao, R. Law, S. Fu, Q. Wu. Identification of flight state under different simulator modes using improved diffusion maps[J]. Optik—International Journal for Light and Electron Optics. 2016, 127(9): 3905-3911.

[22] Hawkins, F.H., Human Factors in Flight[M]. 2nd edn. Ashgate. Brookfield, VT ,1993.

[23] Globerson A, Chechik G, Pereira F, et al. Euclidean embedding of co-occurrence data[J]. Journal of Machine Learning Research, 2007, 8(10): 2265-2295.

[24] 吴春国,梁艳春,孙延凤等.关于SVD与PCA等价性的研究[J].计算机学报，004,27(2):286-288.

[25] Salakhutdinov R, Murray I, On the Quantitative Analysis of Deep Belief Networks[C]// Proc of International Conference on Machine Learning, 2008, 872-879.

[26] Ackley D H, Hinton G E, Sejnowski T J. A Learning Algorithm for Boltzmann Machines[J]. Cognitive Science, 1985, 9(1): 147-169.

[27] ManceraL, Portilla J.L0-norm-based sparse representation through alternateprojection[C]// 2006: 2089-2092．

[28] Lee H, Ekanadham C, Ng A Y.Sparse deep belief net model for visual area V2[C]. 2007: 873-880．

Abnormal Flight States of Aircraft Identification Based on Deep Learning Method

WU Qi CHU Yinxue

(Shanghai JiaoTong University, Shanghai 200240, China)

The quick access recorder(QAR) retains the navigational information of all important flight parameters of the original flight, making it possible to analyze aircraft real-time conditions and ensure flight quality. According to the characteristics of high-dimensional large-scale QAR data, under the background of Big Data, different from the traditional mechanism modeling and analysis of aircraft flight state, the paper uses deep learning to establish a data-driven aircraft flight state recognition model. Based on the study of real QAR flight data, an abnormal flight state recognition program based on the Sparse Restricted Boltzmann Machine is developed. First of all, we use the wavelet de-noising translation method to pre-process the original flight data. And then, we select a series of typical flight parameters, extract the classical time-domain features of these parameters and the mixed entropy feature like Wavelet Singular Entropy to form the feature set. Then we use the Principal Component Analysis technique and the Sparse Restricted Boltzmann Machine to effectively reduce the feature set. Finally, we use four-fold cross validation method. We put the training set into the Gaussian process classifier as a last step. The experimental results show that the flight state recognition based on the Sparse Restricted Boltzmann Machine-Gaussian process classification has high classification accuracy.

flight state recognition; deeping learning; gaussian process

10.19416/j.cnki.1674-9804.2017.03.013

吴奇男，博士，副教授。主要研究方向：人机交互，深度学习，大数据分析。Tel: 021-34204492,E-mail: wuqi7812@sjtu.edu.cn

V226

：A

储银雪男，硕士。主要研究方向：深度学习。Tel: 021-34204492,E-mail: chuyinxue@sjtu.edu.cn