基于X-SBFEM的非线性断裂数值模型研究
傅 兴 安, 李 建 波*, 林 皋
( 1.大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024;2.大连理工大学 建设工程学部 工程抗震研究所, 辽宁 大连 116024 )
基于X-SBFEM的非线性断裂数值模型研究
傅 兴 安1,2, 李 建 波*1,2, 林 皋1,2
( 1.大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024;2.大连理工大学 建设工程学部 工程抗震研究所, 辽宁 大连 116024 )
从非线性断裂力学模型的角度,开展准脆性材料(混凝土)裂纹过程区的有效模拟,是当前的研究热点之一.扩展比例边界有限元法(X-SBFEM)兼有扩展有限元法(XFEM)和比例边界有限元法(SBFEM)两种方法的优势,利用SBFEM求解裂尖段应力奇异性问题,利用XFEM模拟非裂尖段位移场不连续.为在X-SBFEM中增加非线性断裂模型,提出采用side-face力的形式,基于黏聚力模型,通过线性叠加迭代法来模拟准脆性材料(混凝土)裂纹过程区.最后,以数值算例——单边缺口的三点弯曲梁和四点剪切梁——模拟裂纹过程区能量耗散影响,验证了所提方法的精度与应用效果.
扩展比例边界有限元法;应力强度因子;黏聚力;side-face力;裂纹过程区
0 引 言
材料的断裂行为以及断裂过程的数值模拟是评估结构承载能力的重要依据.近几年从断裂力学角度提出的扩展比例边界有限元法(X-SBFEM)是在扩展有限元法[1-2](XFEM)和比例边界有限元法[3-4](SBFEM)的基础上发展而来的.X-SBFEM[5-6]兼有两种方法的优势,在裂纹主体段用XFEM模拟,在裂尖段用SBFEM模拟,最终建立裂纹体的总体平衡方程并进行求解.其中,XFEM的虚自由度与SBFEM的全实自由度的衔接是重点环节.X-SBFEM克服了扩展有限元在域内裂纹尖端近场需要增强函数来描述,且某些情况下,该增强函数将是非多项式或不连续的,造成在形成刚度矩阵时需要特殊处理.而进一步考虑模型裂纹过程区(FPZ)的非线性影响,在X-SBFEM的基础上,引入非线性断裂力学,对于推进模型的应用具有重要工程意义.一般的,准脆性材料裂纹的模拟主要有线弹性的方法(LEFM)和非线性的方法(NFM),用LEFM还是NFM取决于FPZ相对于结构的尺寸[7].现在线弹性力学只能应用在大尺度结构上(如混凝土大坝等)的观点已被广泛接受.为得到更高的计算精度,对于正常尺寸的结构(如混凝土梁)应用基于FPZ的非线性断裂力学模型是有必要的[7].
Yang等[8]、Shi等[9]近年采用FEM-SBFEM耦合的方法或P-SBFEM模拟FPZ的非线性行为时,都通过插入黏聚界面单元(CIEs)来进行分析.这种方法在模拟裂纹扩展过程中,新生成裂纹边界变得扭曲复杂,对于复杂结构模型应用起来有一定的难度[7].
本文提出在X-SBFEM基础上采用线性渐进叠加假设的迭代法求解裂纹面黏聚力来考虑裂纹过程区的非线性影响,并通过对裂纹扩展问题采用基于LEFM的最大环向拉应力准则来预测裂纹路径,模拟裂纹尖端FPZ的能量耗散.
1 扩展比例边界有限元法(X-SBFEM)基本理论
X-SBFEM的主要工作是通过建立裂尖超单元利用SBFEM半解析的性质来模拟裂尖近场的非连续行为,而在裂纹非裂尖段则采用XFEM来描述,关键是单元接触界面处的数值处理.图1是模型域内拓扑关系的示意图[6].
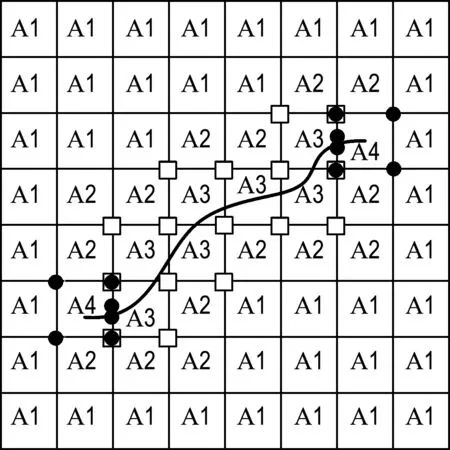
图1 X-SBFEM含裂纹模型域内拓扑关系
1.1 扩展有限元法(XFEM)原理
基于单元分解思想,裂纹的主体段用扩展有限元法进行模拟,其位移场的一般形式为[10]

(1)
式中:Nfem、Nc分别为普通有限元、因被内部裂纹贯穿而增强的节点.N表示形函数.qI为普通自由度,而aJ为与Q所关联的广义自由度(如图1中方形节点所示),Q(x)为Heaviside阶跃函数.扩展有限元平衡方程为
(2)

1.2 比例边界有限元法(SBFEM)原理
如图2所示,考虑裂尖SBFEM超单元内裂纹面有side-face力.首先在不考虑体力的情况下,SBFEM的位移场和应力场为[3]
(3)

(4)
式中:N(η)为边界的形函数,φi和λi分别为特征值及位移模态,ci表示积分常数,D为弹性模量矩阵,L为线性算子矩阵,B1(η)和B2(η)决定于SBFEM超单元的几何特性.根据虚功原理可推得:
(5)

(6)
式中:P为超单元边界等效节点力,Φ为由位移模态为列所组成的矩阵,uh为边界节点位移,E0、E1和E2分别为位移控制方程的系数阵.于是应力强度因子的公式可表达为[6,12]
(7)
式中:KⅠ、KⅡ为两型应力强度因子,L0为裂尖到沿裂纹面延长线与边界相交点的距离.ψyy、ψxy为应力模态.

图2 SBFEM有限域的边界离散及相似坐标变换
Fig.2 Discretization on boundary with element and scaled transformation of coordinates of bounded media of SBFEM
1.3 X-SBFEM耦合模型边界模式
图3描述了一个典型的用XFEM和SBFEM模拟裂纹的方法.SBFEM超单元直接通过单元两条边界来描述裂尖裂纹面,XFEM则由阶跃函数引入附加的自由度来描述裂纹非裂尖段非连续位移场[6].为了保证两种不同单元间的位移连续,则需引入特殊的矩阵T使SBFEM和XFEM衔接节点的位移协调.在把SBFEM得到的未知节点位移(uE、uF、uA和uB)转换成XFEM未知节点位移(q2、q3、a2和a3)的过程中可以根据之前的公式推导出一个转换矩阵,如下式:
(8)
其中I为单位矩阵.为保证位移协调并且把单刚矩阵集入总体刚度阵,需把SBFEM超单元的位移向量和刚度矩阵重新排列,如下式:
(9)
其中usb为SBFEM单元在非共用边界上的节点位移,uxf为XFEM单元在共用边界上的节点位移.转换矩阵T只与SBFEM域和XFEM域共用边界上的裂纹开口处的形函数有关.K表示刚度矩阵,其中下标a表示SBFEM域和XFEM域单元之间共用节点自由度,下标b表示非共用节点自由度.

图3 扩展有限元域与比例边界有限元域的耦合
2 非线性断裂力学模型
2.1 线性渐进叠加假设
Hillerborg等[13]提出的P-a曲线(external load-crack mouth opening displacement curve)是由混凝土结构的裂纹过程区(FPZ)的黏性行为引起的.为简化Xu等[14]求解黏性裂纹扩展的方法,基于线性渐进叠加假设[7],把FPZ当作线弹性裂纹进行求解.
这种线性简化方法中假设塑性变形为0,忽略图4(a)中abp曲线非线弹性部分的影响,即把图4(a)简化成图4(b).由此,图4(b)中B点是线弹性点.这样线弹性断裂力学将可以适用于虚拟的OB段加载的分析.由此,相同材料及几何特性条件下,不同预设裂纹长度的一系列构件将会得到一系列类似的B点.此时,P-a曲线可以当成这一系列B点的包络线.
2.2 开裂准则
混凝土开裂往往呈现复合断裂形态,从数值角度,结构所承受的总荷载如图5(c)所示,除承受外荷载外,在裂纹过程区内,如裂纹面之间相对的位移,包括裂纹面的张裂位移(COD)和滑裂位移(CSD),没有超过图6所示的限值wc和sc时,则还承受虚拟裂纹面内的黏聚力.但裂纹面相对位移超过限值的部分令黏聚力为0.对于有黏聚力的情况,以Ⅰ型应力强度因子为例,应力强度因子由两部分组成[14]:

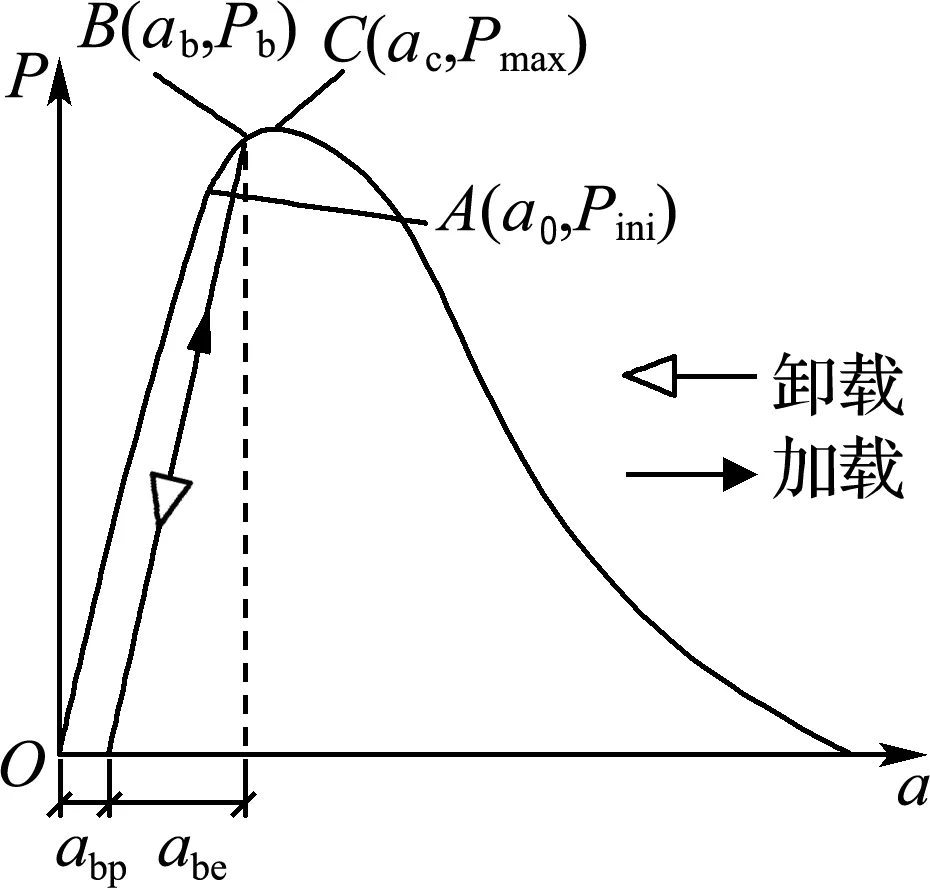
(a) 真实卸载/重加载轨迹

(b) 虚拟卸载/重加载轨迹

图4 线性渐进叠加假设
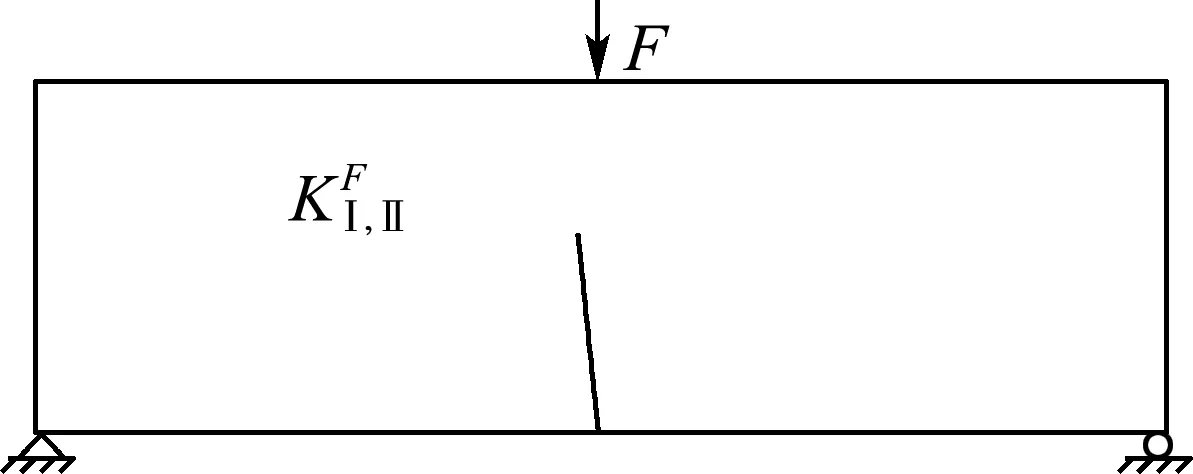
(a) 只有外力作用

(b) 只有黏聚力作用
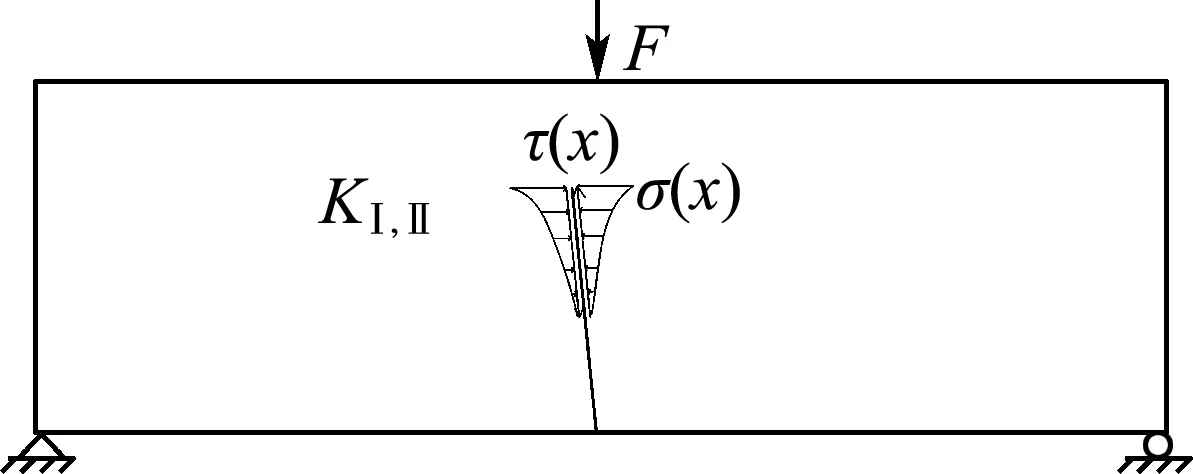
(c) 外力与裂纹面黏聚力叠加作用
图5 叠加法计算应力强度因子KⅠ,Ⅱ
Fig.5 Superposition method for calculating stress intensity factorKⅠ,Ⅱ
(10)

2.3 FPZ软化曲线
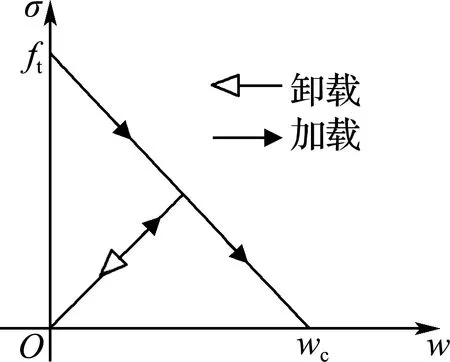
裂纹过程区内的正黏聚力σ(x)决定于图6(a)σ-w双线性的软化曲线或图6(b)σ-w单线性的软化曲线.切分量τ(x)由图6(c)τ-s曲线决定.图6(a)(b)曲线以下的面积为Ⅰ型断裂能GfI.图6(c)曲线间的面积为Ⅱ型断裂能GfⅡ的2倍[8].假设图6中曲线关系都为不可逆的卸载路径,即当裂纹面闭合时,一种弹性的卸载将随着w或s的减小而沿着图中的割线发生.实心箭头表示加载,空心箭头表示卸载.


(a) σ-w双线性关系
(b)σ-w单线性关系

(c)τ-s关系
图6 裂纹相对位移与黏聚力的关系
Fig.6 Relations between relative displacements of crack and cohesive tractions
2.4 以迭代形式模拟黏聚力模型
本文工作的关键是根据裂纹面的相对位移采用线性叠加的迭代法求解裂纹面黏聚力.
步骤1假设结构只受外力F作用,这样可以根据X-SBFEM基于线弹性假定求出超单元裂纹面相对位移Δui,再根据图6即可得出相应黏聚力ti.
步骤2如图5,把外荷载F和步骤1中得到的黏聚力ti一起作用在结构上.其中黏聚力以side-face力形式施加在裂纹面上.
side-face力分布荷载[5]对应的虚功项为

(11)
易得SBFEM非齐次控制方程:

(12)
假定荷载及位移模式能由幂级数表达,即
(13)

(14)
将式(14)代入式(12)和式(13)可得

(15)

(16)
因此,边界节点完整位移和等效节点力分别为

(17)
(18)
其中Φ和Q分别为式(6)解出的位移模态矩阵和力的模态矩阵.综合式(17)和式(18)可得

(19)
故由side-face力形式加载的黏聚力产生的SBFEM等效边界节点力为

(20)

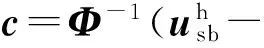
(21)
则可得到SBFEM超单元的位移场为
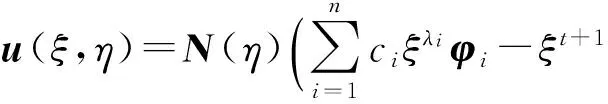
(22)
式中:φt为SBFEM解出的应力模态.由式(22)求解出相对位移Δui+1.
步骤3重复步骤1、2直至ti与Δui+1的关系能很好地符合图6中的关系.
3 算例与分析
3.1 单边缺口三点弯曲梁
Hillerborg等曾通过试验研究单边缺口三点弯曲梁模型[13],梁的材料和几何尺寸数据等如图7所示.抗拉强度ft=3.33 MPa,Ⅰ型断裂能GfⅠ=137 N/m.本算例基于LEFM最大环向拉应力准则来预测裂纹扩展路径.单线性软化曲线(图6(b)) 被用来做分析.由Ⅰ型断裂能GfⅠ所得出的单线性软化曲线限值为wc=0.082 3 mm.计算了在20×200网格密度条件下3种裂纹扩展步长10、20和30 mm的结果,并与基于线弹性方法[6]的结果进行对比.
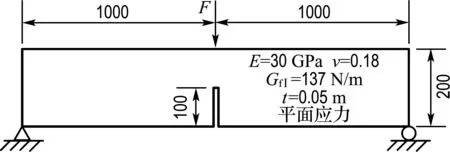
图7 单边缺口三点弯曲梁
图8是考虑FPZ非线性的3种不同裂纹扩展步长时的荷载-加载点位移曲线.由图中可以看出,陈白斌等[6](基于X-SBFEM) 和Yang等[8](基于SBFEM)基于LEFM结果数据与Hillerborg等的试验数据[13]有很大的差别,尤其是他们的荷载峰值都比试验的峰值高出较多.这是因为基于线弹性断裂力学方法无法模拟FPZ的能量耗散.而从图中可以看出本文方法计算得到的结果与试验结果[13]是较为符合的,说明本文中所使用的基于X-SBFEM 通过线性叠加的迭代法求解黏聚力的方法能很好地模拟FPZ的能量耗散.而且从图中可以看出3种裂纹扩展步长的结果都很符合试验曲线,这说明不同裂缝扩展步长对计算结果影响不大.
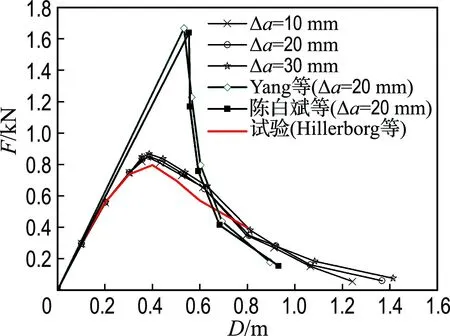
图8 基于非线性断裂力学不同裂纹扩展步长时三点弯曲梁的荷载-加载点位移曲线
Fig.8 NFM-based load-LPD curves for three-point bending beam with different crack increment lengths
3.2 单边缺口四点剪切梁
Arrea和Ingraffea曾试验和分析了单边缺口四点剪切梁模型[15].其几何尺寸及材料参数如图9所示.假设为平面应力状态.抗拉强度ft=3.00 MPa,Ⅰ型断裂能GfⅠ=100 N/m,Ⅱ型断裂能GfⅡ=10 N/m.裂纹路径预测基于LEFM最大环向拉应力准则.单线性的软化曲线(图6(b))和τ-s曲线(图6(c))被用来做分析.由Ⅰ型断裂能GfⅠ=100 N/m计算得到的COD限值wc=0.067 mm,由Ⅱ型断裂能GfⅡ求得的CSD限值sc=0.02 mm.计算了在20×200网格密度条件下3种裂纹扩展步长20、30和40 mm的结果,并与基于线弹性方法[6]的结果进行对比.
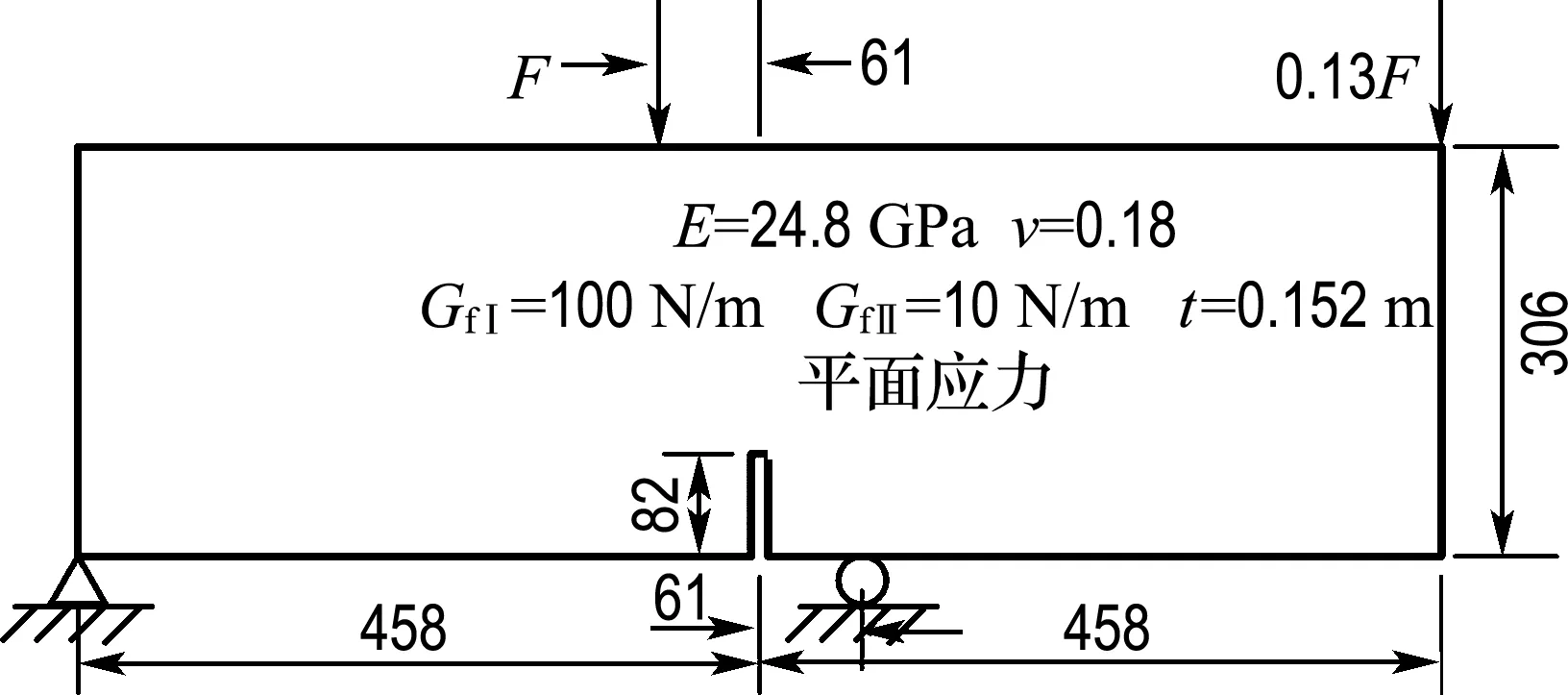
图9 单边缺口四点剪切梁
图10和图11分别展示了基于本文方法计算得到的不同裂纹扩展步长下荷载与裂纹口滑移位移的关系曲线、荷载与其加载点位移关系的曲线.其中,由图10可以看出,本文计算结果与Arrea和Ingraffea试验得到的数据[15]及Yang等[8](基于NFM)的数值解拟合较好;从图11可以看出,本文计算结果与Yang等[8](基于NFM)的数值解较为接近,峰值都明显低于陈白斌等[6](基于X-SBFEM、LEFM)所得的数值解结果,说明本文方法较好地基于X-SBFEM算法模拟了裂纹尖端存在FPZ能量耗散的影响.且由图看出3种裂纹扩展步长的结果接近,即裂纹扩展步长对计算结果的影响不是很大,从而验证了X-SBFEM算法对于复合型裂纹扩展问题的适用性.此外,图11可看成本文方法较好地表现出荷载-加载点位移曲线snap-back的现象.图12所示为当a=20 mm时F=36.7 kN作用下的裂纹轨迹及正黏聚力沿裂纹面分布图.
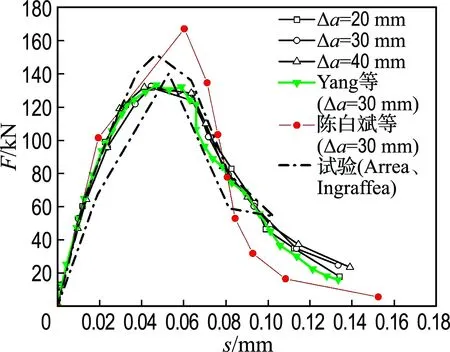
图10 基于非线性断裂力学不同裂纹扩展步长下的荷载-滑移位移曲线
Fig.10 NFM-based load-CMSD curves with the change of crack increment length
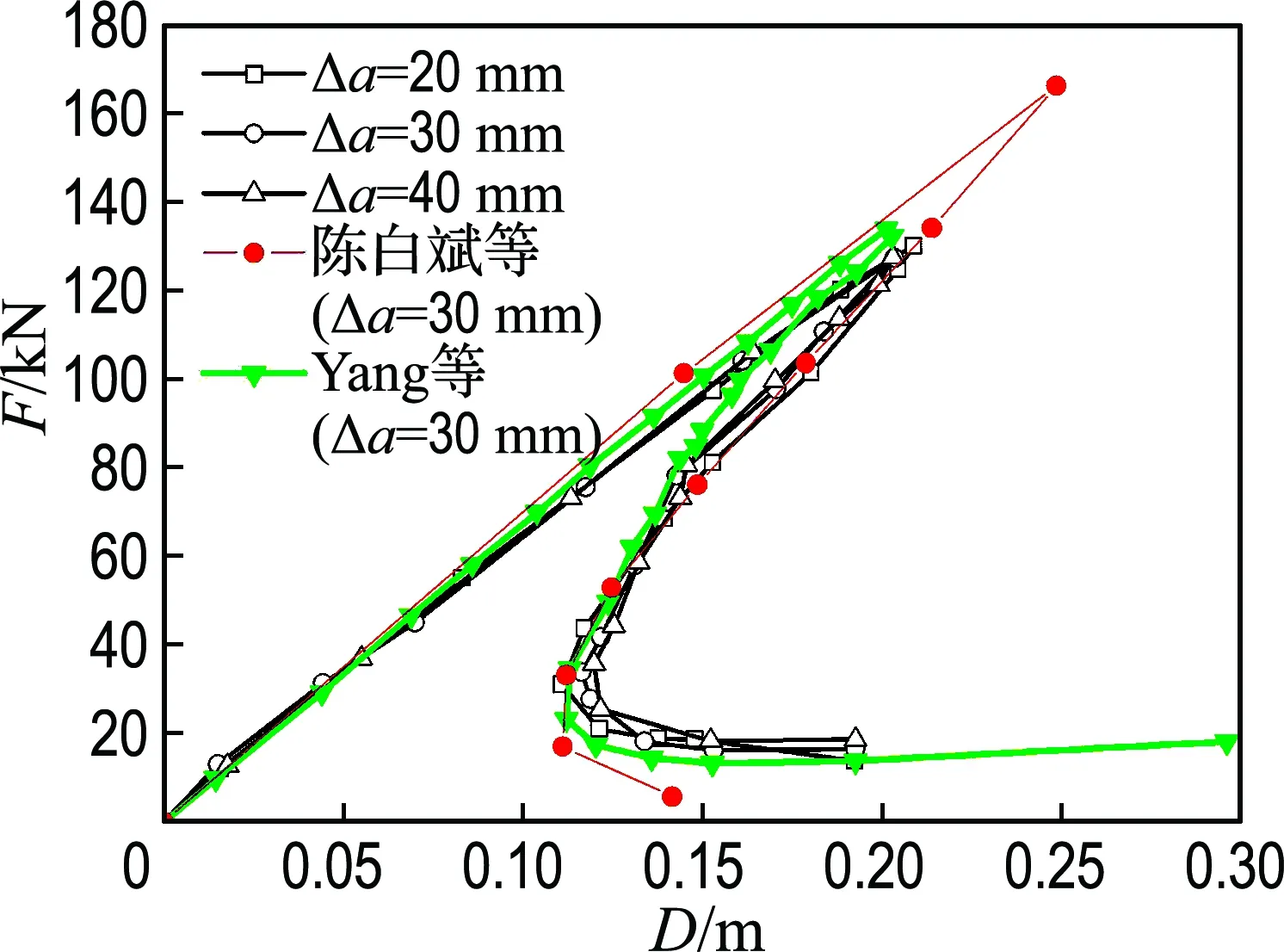
图11 基于非线性断裂力学不同裂纹扩展步长时四点剪切梁的荷载-加载点位移曲线


(a) 变形几何图
4 结 语
本文提出基于扩展比例边界有限元法(X-SBFEM)采用线性叠加迭代法模拟准脆性材料(混凝土)裂纹过程区的非线性行为,并将其结果与基于X-SBFEM采用LEFM方法得到的结果进行对比,可以看出其模拟裂纹尖端FPZ的能量耗散的有效性.本文发展了X-SBFEM在非线性断裂过程模拟中的应用.此外,采用该方法不需要插入CIEs和引入影子域(shadow domain)就可以得到较高精度的结果.
[1] RABCZUK T, BORDAS S, ZI G. On three-dimensional modelling of crack growth using partition of unity methods [J].ComputersandStructures, 2010,88(23/24):1391-1411.
[2] BELYTSCHKO T, GRACIE R, VENTURA G. A review of extended/generalized finite element methods for material modeling [J].ModellingandSimulationinMaterialsScienceandEngineering, 2009,17(4):043001.
[3] SONG Chongmin, WOLF J P. Semi-analytical representation of stress singularities as occurring in cracks in anisotropic multi-materials with the scaled boundary finite element method [J].ComputersandStructures, 2002,80(2):183-197.
[4] SONG Chongmin, TIN-LOI F, GAO Wei. A definition and evaluation procedure of generalized stress intensity factors at cracks and multi-material wedges [J].EngineeringFractureMechanics, 2010,77(12):2316-2336.
[5] 陈白斌,李建波,林 皋. 无需裂尖增强函数的扩展比例边界有限元法[J]. 水利学报, 2015,46(4):489-496, 504.
CHEN Baibin, LI Jianbo, LIN Gao. An extended scaled boundary finite element method without asymptotic enrichment of the crack tip [J].JournalofHydraulicEngineering, 2015,46(4):489-496,504. (in Chinese)
[6] 陈白斌,李建波,林 皋. 基于X-SBFEM的裂纹体非网格重剖分耦合模型研究[J]. 工程力学, 2015,32(3):15-21.
CHEN Baibin, LI Jianbo, LIN Gao. Study on the coupling model of crack without remeshing based on X-SBFEM [J].EngineeringMechanics, 2015,32(3):15-21. (in Chinese)
[7] 朱朝磊. 基于比例边界有限元方法的混凝土结构静动态断裂模拟[D]. 大连:大连理工大学, 2014.
ZHU Chaolei. Static and dynamic fracture simulation of concrete structures based on scaled boundary finite element method [D]. Dalian:Dalian University of Technology, 2014. (in Chinese)
[8] YANG Z J, DEEKS A J. Fully-automatic modelling of cohesive crack growth using a finite element-scaled boundary finite element coupled method [J].EngineeringFractureMechanics, 2007,74(16):2547-2573.
[9] SHI Mingguang, ZHONG Hong, OOI E T,etal. Modelling of crack propagation of gravity dams by scaled boundary polygons and cohesive crack model [J].InternationalJournalofFracture, 2013,183(1):29-48.
[10] 茹忠亮,朱传锐,赵洪波. 裂纹扩展问题的改进XFEM算法[J]. 工程力学, 2012,29(7):12-16.
RU Zhongliang, ZHU Chuanrui, ZHAO Hongbo. An improved algorithm of XFEM for the crack propagation problems [J].EngineeringMechanics, 2012,29(7):12-16. (in Chinese)
[11] 张晓东,丁 勇,任旭春. 混凝土裂纹扩展过程模拟的扩展有限元法研究[J]. 工程力学, 2013,30(7):14-21.
ZHANG Xiaodong, DING Yong, REN Xuchun. Simulation of the concrete crack propagation process with the extended finite element method [J].EngineeringMechanics, 2013,30(7):14-21. (in Chinese)
[12] 刘钧玉,林 皋,胡志强. 裂纹面荷载作用下多裂纹应力强度因子计算[J]. 工程力学, 2011,28(4):7-12.
LIU Junyu, LIN Gao, HU Zhiqiang. The calculation of stress intensity factors of multiple cracks under surface tractions [J].EngineeringMechanics, 2011,28(4):7-12. (in Chinese)
[13] HILLERBORG A, MODEER M, PETERSSON P E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements [J].CementandConcreteResearch, 1967,6(6):773-781.
[14] XU Shilang, REINHARDT H W. Determination of double-Kcriterion for crack propagation in quasi-brittle fracture. Part Ⅱ: Analytical evaluating and practical measuring methods for three-point bending notched beams [J].InternationalJournalofFracture, 1999,98(2):151-177.
[15] ARREA M, INGRAFFEA A. Mixed-mode crack propagation in mortar and concrete: 81-13 [R]. Ithaca: Department of Structural Engineering, Cornell University, 1982.
StudyofnumericalmodelofnonlinearfracturebasedonX-SBFEM
FU Xing′an1,2, LI Jianbo*1,2, LIN Gao1,2
( 1.State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China; 2.Institute of Earthquake Engineering, Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, China )
The effective simulation of the fracture process zone (FPZ) of quasi-brittle material (concrete) by using nonlinear fracture mechanics model is one of the hot spots in the current research. Extended scaled boundary finite element method (X-SBFEM) has advantages of both extended finite element method (XFEM) and scaled boundary finite element method (SBFEM), making full use of XFEM to describe discontinuous displacement field in non-crack-tip area and SBFEM to precisely solve stress singular problems in the crack-tip area. For the application of nonlinear fracture models in X-SBFEM, based on the model of the cohesive traction, the FPZ of the quasi-brittle material (concrete) is simulated using the iterative method of linear superposition by the form of side-face traction. Finally, numerical examples of the three-point single notched bending beam and the four-point single notched shear beam are used to simulate the energy dissipation effect in the FPZ, which verify the accuracy and application effect of the proposed method.
extended scaled boundary finite element method (X-SBFEM); stress intensity factor; cohesive traction; side-face traction; fracture process zone (FPZ)
2016-09-18;
2017-05-26.
国家重点研发计划资助项目(2016YFB0201000);国家自然科学基金资助项目(51779222);国家自然科学基金委创新研究群体项目(51421064);中央高校基本科研业务费专项资金资助项目(DUT17LK16).
傅兴安(1991-),男,硕士生,E-mail:fuxingan@mail.dlut.edu.cn;李建波*(1977-),男,博士,副教授,E-mail:jianboli@dlut.edu.cn;林 皋(1929-),男,教授,中国科学院院士,E-mail:gaolin@dlut.edu.cn.
1000-8608(2017)05-0494-07
TV313
A
10.7511/dllgxb201705009

