纳米级晶粒间小角度晶界应变场的实验研究

董照实

(南京理工大学 材料科学与工程学院，江苏 南京 210094)

晶界是金属及合金中普遍存在的缺陷，材料的宏观强度强烈地依赖于晶界的凝聚力[1-2]。晶粒与晶粒间的晶界以及组成晶界的位错对材料的塑性变形起着很重要的作用。除了力学性能外，晶界对材料的光学、磁学和电学性质影响都很大。对晶界的研究一直是材料科学中的热点方向[3-5]。小角度晶界由分布在两个稍有不同取向的晶体上的离散位错组成。小角度晶界的结构可以用位错模型来解释，即小角度晶界可以看作是由一系列位错所组成。Taylor[6]首次提出了小角度晶界的位错模型，Read和Shockley[7]进一步改进了该模型，将其用于预测位错密度。位错模型是理解小角度晶界的基础，然而实验测量的应变场将有助于了解真实的小角度晶界结构以及它们如何影响材料的性质。

以往在高分辨透射电子显微镜图像上直接测量位移多用极值点定位法[8]，该方法通常需要经过降低噪声、极值点确定、网格计算和应变分析等步骤。其基本思路是当两个二维网格叠加时会形成云纹，第一个网格是由实验得出的电子显微图像，第二个网格是由第一个网格中的未变形区域计算得出。由分析结果云纹图，电子显微图像中相对于计算网格的局域位移可以被测出，进而可以计算应变和应变层的厚度。但该技术的测量精度有限，很难精确测量纳米尺度的应变。随着电子显微分析技术的发展，近些年发展出了几何相位分析技术[9]，其方法是将高分辨图像进行傅立叶变换后选择两个非线性矢量,然后再进行反傅立叶变换,即可得到微观测量尺度上的、高精度的位移场和应变场。该方法已成为纳米尺度形变场分析领域的强有力工具[9]。几何相位分析在各种系统中都具有很好的适用性，如量子点[10]，纳米结构[11]，纳米线[12]，异质结构[13]，纳米团簇[14]和晶体管[15]。该技术的测量精度高达0.003 nm[8]。

在这篇文章中，我们利用高分辨透射电子显微镜和几何相位分析技术分析了小角度晶界结构的变形场。

1 多晶金晶界实验研究

1.1 高分辨透射电子显微镜实验

本研究所使用的样品为多晶金，面心立方结构，泊松比0.44，晶格常数aAu=0.408 nm，晶面间距d100=0.204 nm。首先将测试样品进行机械减薄到50 μm，再用离子磨减薄到一定的厚度，得到大面积的薄区。将试样放在铜支持网上，再将支持网放在透射电子显微镜的双倾台架上，用透射电子显微镜观察晶界结构。拍摄高分辨图像所使用的透射电子显微镜为JEM-2010。工作时的加速电压200 kV，球面像差1 mm，点分辨率0.194 nm。高分辨透射电子显微镜图像通过Gatan 1k×1k慢扫描电荷耦合元件(CCD)摄像机采集得到数字电子显微图像，如图1所示。

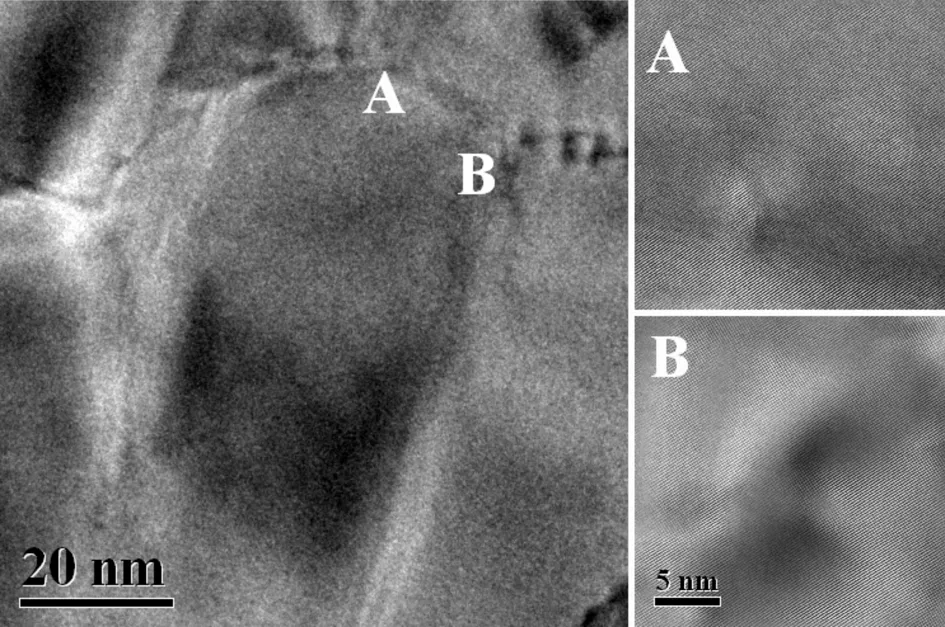
图1 多晶金的高分辨透射电子显微镜图像

1.2 几何相位分析实验

沿着晶带轴拍摄的高分辨图像可以被看做试样原子面对应的干涉条纹。几何相位分析这些干涉条纹并分别提取每个条纹的位移信息。为了更加真实，该技术可以选定某一未受应力影响的区域为基板，假定其为完美的晶格。通过对比基板计算出其它晶格条纹的位移。该方法是基于计算晶格条纹的局部傅里叶分量。局部傅里叶分量的相位或几何相位Pg(r)直接与倒格矢g方向的位移场u(r)相关联。

Pg(r)=-2πg·u(r)

假定实验试样中的位移场沿传播方向是恒定的，如果有小的变化，取他们的平均值。通过测量两相个位图像Pg1(r)和Pg2(r)，就可以确定二维位移场：

在里，a1和a2是真实空间晶格矢量，g1和g2是倒格子空间对应的矢量。上面公式的矩阵形式为：

换算成平面应变可以写为：

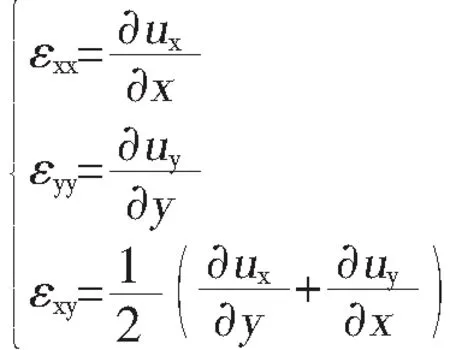
几何相位分析方法的基本步骤为：1)将高分辨电子显微图像做傅立叶变换；2)在傅立叶空间选择两个不代表同一晶面组的强衍射斑做反傅立叶变换，计算出来的傅立叶变换图像是一个复数图像，这个复数图像的相位成分与局域原子面位移有着定量关系；3)通过两晶面组的相位成分计算二维位移场，局域应变张量成分exx，eyy和exy可以由计算位移场的微分得到,同时还能计算刚体旋转wxy。

2 实验结果及讨论

图1显示的是多晶金晶粒的透射电子显微镜图像，晶粒的宽度为30 nm左右，长度为50 nm左右。我们在晶粒上部晶界上A，B两个位置拍摄了放大的晶界图像，如图右侧所示。A部位上下晶粒间的角度差约2(°)。B部位左右晶粒间的角度差约3(°)。A部位的晶界较窄，而B部位的晶界较宽。

图2(a)和2(d)为A，B两个晶界图像经过傅立叶滤波后的图像。

图2 傅立叶滤波后的晶界图像以及晶界的exx和eyy应变

傅立叶滤波可以去掉透射电子显微镜拍摄过程中引入的噪声，提高应变分析图像的清晰度及精确度。对图2(a)和(d)进行几何相位分析后的应变场显示在图2右部。进行几何相位分析时选取的坐标系为平面直角坐标系，横轴为x轴，纵轴为y轴。图2(b)和2(c)分别为图2(a)x和y轴方向的应变。图2(e)和2(f)分别为图2(d)x和y轴方向的应变。应变值的大小用温度色标表示，最大显示应变为+10%，对应于白色；最小显示应变为-10%，对应于黑色。四幅应变图中，在远离位错芯的红绿相间区域应变都接近于零。图2(b)和2(c)的上部的畸变很小，基本没产生位错。而图2(e)和2(f)中晶界两边都有位错分布。应变场显示，位错不规则分布在晶界上，晶界中心线附近位错密度最大。远离晶界中心线时，位错密度会减小。为了对比应变场中的位错，我们选取图2中编号为1～8的8个位错，分别测量了这些位错垂直于伯格斯矢量方向的应变值，结果如图3所示。1～7号位错距离其他位错的距离在1～2 nm之间，8号位错远离其它位错。通过图3可以看出，1～7号位错与8号位错的应变值并没有明显的差距。只有5号位错的应变值略大于8号，因为5号位错距离其它位错的距离最近，受到其它位错的影响最大。而且5号位错位于晶界分界线部位，也会受到产生应变的其它因素的影响，比如两个晶粒间的取向差。尽管如此，5号位错受到的影响也是比较小的，在应变图中位错间距较小的部位，位错的应变场发生了严重的畸变。

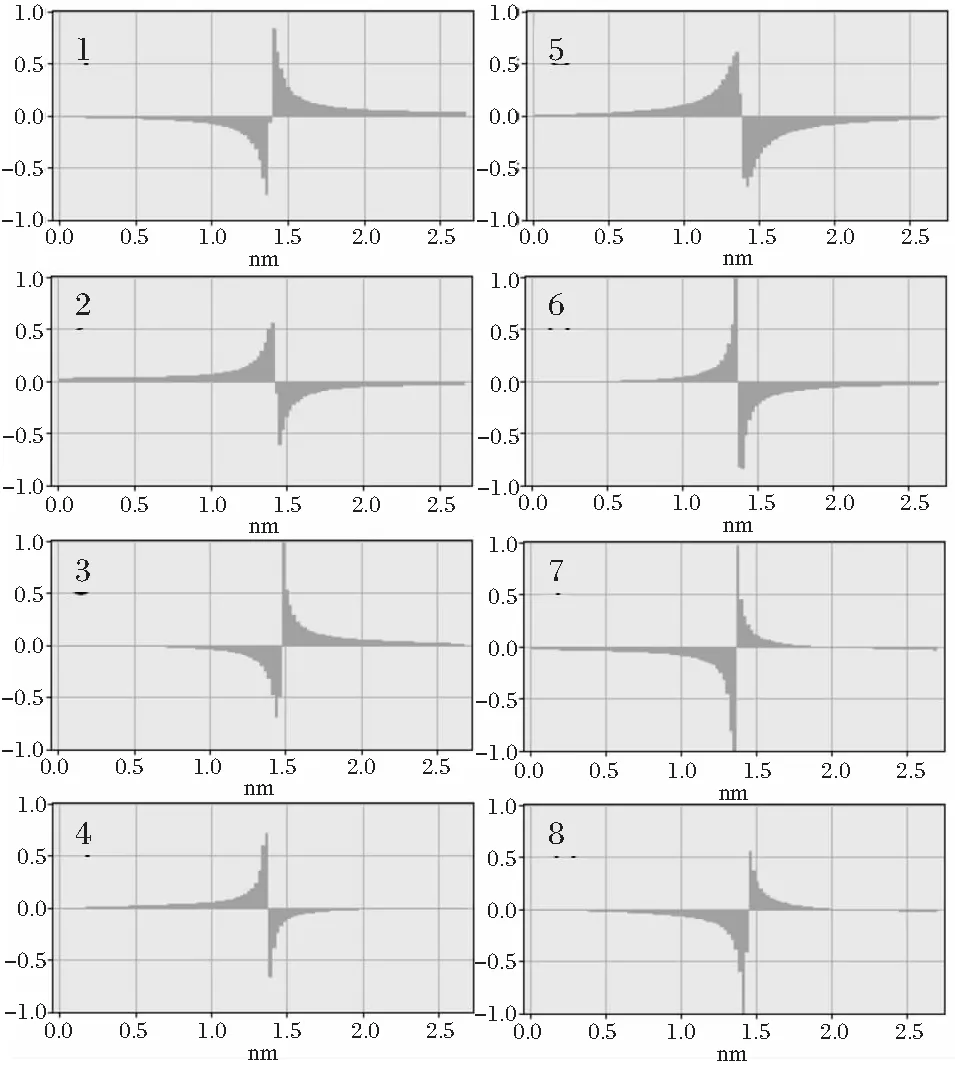
图3 位错芯部位的应变值

3 结 论

在本研究中采用了高分辨透射电子显微镜观察，并使用具有纳米级测量灵敏度和空间分辨率的实验力学测试方法——几何相位技术，作为电子显微镜图像的分析手段，测量了多晶金小角度晶界的应变场。通过对该晶界应变分布图的研究发现，晶界附近的位错排列是非常不规律的。晶界分界线部位的位错密度非常大，远离晶界的部位位错密度较小。通过对比位错间的应变发现，当两个位错间的距离大于1 nm时，其相互影响变小。只有在位错间距非常小时才会发生强烈的相互作用，比如在位错密度非常高的晶界分界线部位，位错应变场严重变形。