基于实时稳态模型的汽轮机冷端系统闭环优化控制

李建平，吕海涛，张建忠，李 华，胡 勇，钟祎勍，王剑钊，王保民

(1. 华能瑞金发电有限责任公司, 江西 瑞金 341108；2.中国华能集团清洁能源技术研究院有限公司, 北京 102209)

基于实时稳态模型的汽轮机冷端系统闭环优化控制

李建平1，吕海涛1，张建忠1，李 华1，胡 勇2*，钟祎勍2，王剑钊2，王保民2

(1. 华能瑞金发电有限责任公司, 江西 瑞金 341108；2.中国华能集团清洁能源技术研究院有限公司, 北京 102209)

汽轮机冷端系统是火电机组的重要辅助系统，其运行状态的好坏直接关系到机组的安全、经济运行。分析汽轮机冷端系统的换热机理，通过对汽轮机末级变工况计算模型、凝汽器换热变工况计算模型以及变频循环水泵变工况特性分析，建立汽轮机冷端系统最佳真空稳态计算模型。分析了机组在不同边界条件下的最佳运行真空，进而利用稳态计算模型构建最佳真空闭环优化实时控制系统，实现对机组循环冷却水流量的连续调节，提高了机组的运行经济性。

冷端系统；最佳真空；循环水泵变频；闭环优化

随着国家对火电机组节能减排要求的不断提高，节能降耗成为火电发电亟待解决的问题，已成为各个发电集团实现可持续发展的方向。其中，提高火电机组的发电效率主要可以采取以下方式：对火电机组的设备进行改造和优化、对机组的运行参数进行优化、对机组的运行方式进行调整和优化，以及对机组关键控制系统进行优化。本文对汽轮机冷端系统的优化主要从运行参数优化以及控制系统优化两个方面着手来提高机组的运行经济性。

汽轮机冷端系统用于维持一定的真空，其对机组运行的安全性和经济性有直接的影响。对于超临界火电机组，每当背压变化1 kPa时，将影响1%～2%汽轮机出力；此外，汽轮机背压通过机组循环水流量来进行调节，循环水泵是电厂的主要耗电设备，在机组厂用电率中占有较大的比重。当冷端系统出现问题时将直接导致凝汽器真空降低，汽轮机的热效率下降，机组供电煤耗上升，将直接危及汽轮机末级的安全运行。

以常规湿冷火电机组为例，其汽轮机冷端系统主要通过循环水泵来调节凝汽器真空，现有机组中循环水泵大部分均采取工频泵或者双速泵两种形式，由于只能通过启停泵方式来改变循环水流量，无法实现循环水流量的连续调节，机组无法达到理论上的最优真空运行状态；其次，由于大功率循环水泵启停需要耗费较长时间，现有的汽轮机冷端优化系统均采取离线计算方式，给出运行优化指导，运行人员仍需对循环水泵启停进行手动干预，且调节缺乏实时性。

但是，随着对大功率循环水泵进行变频改造，从而为汽轮机冷端系统最佳真空实时控制提供了可能。本文通过对冷端系统闭环优化控制的研究，摆脱传统参数定值优化中优化分析结果与实时控制脱节的局限性，将在线实时优化结果传送至机组实时控制系统中，实现对机组真空的连续调节，提高汽轮机的热经济性，对火电机组节能降耗具有重要的意义。

本文将针对常规湿冷机组冷端特性展开研究，通过对冷端系统凝汽器特性、汽轮机末级特性及变频循环水泵特性展开研究，建立其稳态计算模型，进而以稳态计算模型为基础根据不同环境温度和负荷，确定机组的最佳运行真空，并以此作为控制目标，构建汽轮机冷端实时控制系统，通过对循环水流量的连续调节实现对汽轮机冷端系统的闭环优化控制。

1 汽轮机冷端优化原理

当汽轮机首端参数和环境水温保持不变时，随着循环水流量的改变，汽轮机的末级排汽压力将会跟随发生变化，而汽轮机末级压力与机组的级间效率紧密关联，当机组末级压力发生改变时将改变机组的级间效率，蒸汽做功的有效焓降将会变化，从而致使汽轮机出力发生变化。当末级排汽压力下降时，蒸汽在末级中的做功能力将会提升，汽轮机末级蒸汽的焓值下降，蒸汽的效焓降升高，机组出力将会上升；反之亦然。而汽轮机末级排汽压力、排汽焓值等排汽参数由汽轮机冷端系统的工作性能所决定。在相同的蒸汽参数和外界环境温度下，汽轮机冷端系统的冷凝效果取决于凝汽器的换热特性和机组循环水流量，由于凝汽器的换热特性无法进行改变，因此只能通过调节机组循环水流量来改变机组末级的工作状态，对于经过变频改造后的循环水系统，随着变频器频率上升循环水泵转速增加，增大循环水流量将会降低末级排汽压力，汽轮机出力得到提升的同时循环水泵功耗也在增加，只有当汽轮机功率增量大于循环泵耗功增量时，调节才有益于机组的经济运行，这就是汽轮机冷端优化的原理。

2 冷端系统稳态模型

图1为常规湿冷机组冷端系统结构简图。

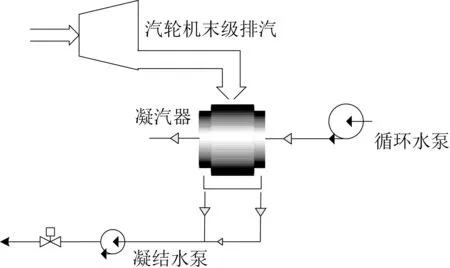
图1 湿冷机组冷端系统结构示意图

汽轮机末级排汽经过联通管道送至凝汽器中，循环冷却水则通过凝汽器中的换热管束对管外排汽进行冷却，低压缸末级乏汽在管束表面则冷凝为饱和水并汇入至凝汽器热井中，因此根据常规湿冷机组凝汽器的换热机理可得：

(1)管外蒸汽冷凝释放的热量

Qa=Dc(hc-cpwtn)

(1)

式中Qa——末级排汽冷凝释放的热量，kJ/s；Dc——末级排汽量，kg/s；hc——末级排汽焓，kJ/kg；tn——凝结水饱和温度，℃；cpw——凝结水比热容，kJ/(kg·℃)。

(2)管内循环冷却水吸收的热量

Qb=Dwccw(ta2-ta1)

(2)

式中Qb——循环冷却水吸收的热量，kJ/s；Dw——机组循环冷却水流量，kg/s；ta1——循环冷却水入口水温，℃；ta2——循环冷却水出口水温，℃；ccw——循环冷却水的比热容，kJ/(kg·℃)。

(3)凝汽器传热速率方程

Q=KFΔtm

(3)

式中K——凝汽器的换热系数；F——凝汽器的换热面积，m2；Δtm——对数平均温差，℃。

在稳态工况下，根据凝汽器的换热机理并结合能量守恒定律，汽轮机低压缸末级排汽冷凝释放的热量应该与管内循环冷却水吸收的热量相等，即：

Qa=Qb=Q

(4)

从式(4)中可以得出，汽轮机末级排汽终参数将由凝汽器特性以及循环水泵的特性共同决定，而他们之间又是相互影响和相互制约，因此将从汽轮机末级、凝汽器及循环水泵3个方面对汽轮机冷端系统稳态计算模型进行研究。

2.1汽轮机末级变工况计算

为了方便计算机组的凝汽器压力，定义凝汽器的换热效率及传热单元数[1-2]，其表示为

(5)

(6)

将式(1)～式(6)联立求解，蒸汽冷凝后的饱和温度可以表示为

(7)

式(7)中，tn为汽轮机乏汽冷凝后的饱和水温度，根据水蒸气和水的热力性质，在饱和状态下压力和温度是一一对应的，因此根据经验公式凝汽器压力可以表示为

(8)

从式(7)、式(8)中可以看出，在凝汽器换热系数、循环冷却水温度及机组末级排汽终参数不变的条件下，凝汽器压力只受循环冷却水流量的影响。而当末级排汽压力发生变化时，冷端系统中的蒸汽末级排汽焓和末级排汽量均会改变，影响蒸汽在汽轮机末级中的做功。

(1) 汽轮机末级压力将会随着机组末级排汽压力的改变而改变，而末级压力的变化将会导致末级的级间效率发生变化，从而导致汽轮机末级排汽焓发生改变。以汽轮机组第(i+1)级为例，其级间效率可以表示为[1-3]

(9)

根据式(9)，汽轮机第(i+1)级抽汽的焓值可以表示为

hi+1=hi-ηi，i+1(hi-hi+1)

(10)

式中ηi，i+1——汽轮机第(i+1)级的级间效率；hi、hi+1——第i、(i+1)级的抽汽焓值，kJ/kg；hi+1——第(i+1)级的理想抽汽焓值(即：等熵焓值)。

在末级排汽焓的计算中，首先需寻找过热蒸汽与湿蒸汽的分界点。分界点之前的各级抽汽，认为级组的压比不变，故其级间效率也不变；而分界点之后的各级蒸汽，认为其做功过程为理想绝热膨胀过程，所以蒸汽第i级抽汽的熵值等于第(i+1)级抽汽的理想熵值，即：si+1=si，结合第(i+1)级抽汽压力pi+1，即可求得第(i+1)级的抽汽理想焓值hi+1，从而根据式(10)得到第(i+1)级的抽汽焓值。

机组的级间效率由级间压比所决定，其可以表示为

ηi，i+1=f(pi+1/pi)

(11)

对于级间效率则可以根据汽轮机热平衡图参数计算其在不同负荷工况下的级间效率和级间压比，进而拟合级间压比和级间效率之间的函数关系式，即可根据级间压力求得汽轮机在不同负荷工况下的级间效率，其关系曲线如图2所示。

(2)从式(7)中可以看出，当凝汽器内循环冷却水流量发生改变时，凝汽器内饱和水温度将会发生变化，当凝结水通过末级低压加热器时，将致使其抽汽流量发生变化，最终导致做功蒸汽量和末级排汽量的变化，而当排汽量发生变化时，凝汽器的热负荷也相应改变并再次影响至凝汽器压力。

当末级排汽压力发生改变时，可采用汽轮机回热系统的热经济性状态方程[4-5]，重新确定汽轮机各级抽汽量及末级排汽量，其可以表示为：

Dc=D0-∑Di-∑Dk

(12)

Di=A-1(D0τ-AkDk-Qrl)

式中Di——各级抽汽量Di组成的列向量；Dk——进出各级加热器的辅助蒸汽或辅助水Dki组成的列向量；D0——主蒸汽流量；Dc——末级排汽量；A、Ak——各级抽汽放热量、给水焓升、疏水放热量组成的系统状态矩阵；τ——各级给水焓升组成的列向量；Qrl——各环节纯热量利用组成的列向量。

当末级排汽量和排汽焓重新确定之后，由式(1)可知，汽轮机末级排汽释放的热量又将发生变化，从而使得公式(4)不再成立，此时则需重新对汽轮机末级排汽压力进行求解，直至计算收敛为止。

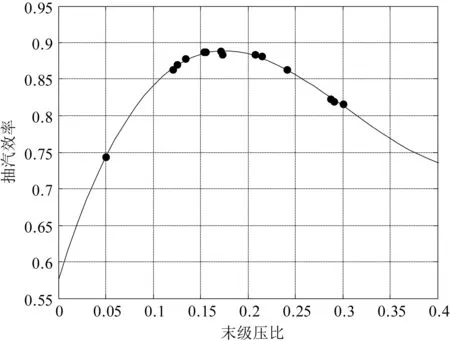
图2 级间效率与压比关系曲线

2.2凝汽器传热系数变工况计算

汽轮机末级排汽与循环冷却水进行热交换时存在3个换热过程，分别为：管道外蒸汽的冷凝换热、凝汽器管壁的热传导以及管内的循环冷却水吸热，则凝汽器的换热系数可以表示为[6-7]

(13)

式中εi，εo——管内、外的污垢热阻；αi为管内换热系数；αo——管外换热系数；λ——管壁的导热系数；Fi，Fo——管内、外的换热面积；Fm——管壁的对数平均面积；δ——管壁厚度。

在某一工况下当凝汽器内表面洁净度保持不变时，凝汽器换热系数只取决于循环冷却水流量和循环冷却水入口温度，因此变工况下凝汽器的换热系数可以表示为[3]

(14)

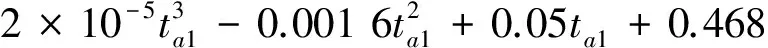
(15)

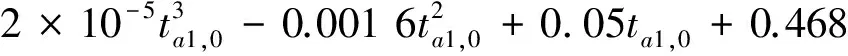
(16)

式中βti，βt0——变工况和参考工况下的循环水入口水温修正系数。

2.3变频循环水泵变工况计算

根据泵与风机特性，机组循环水流量由循环水泵特性和凝汽器管道阻力特性共同决定。根据循环水泵的性能曲线，其流量与扬程间的关系利用多项式进行拟合[8-9]，其可以表示为

(17)

式中 Δp——循环水泵的扬程；Dw——循环水流量；fi——多项式拟合系数。

而凝汽器管道的阻力特性曲线一般为抛物线[8,9]，可以根据典型工况下泵的工作点进行拟合得到，可以表示为

(18)

式中 Δps——循环水经过管道后产生的压降；fns——管道的阻力系数。

当循环水泵转速发生变化时，其泵运行曲线亦发生改变，假设当前循环水泵的转速为n，额定转速为n0，转速比为α=n/n0，根据变频泵的特性，当转速为n时，循环水泵特性曲线[10]可以表示为

(19)

联立公式(18)、式(19)，便可求得转速为n时机组的循环水流量。进而根据相似原理，转速为n1时循环水泵功率可以表示为

(20)

式中 下标1——变工况；下标0——额定工况；Pf——泵功率；ρ——循环水密度，其与循环水温度有关；n表示循环水泵转速。

3 冷端系统实时闭环优化控制

3.1凝汽器最佳真空计算

通过变频电机改变循泵转速来实现对循环水流量的调节，当循环水流量变化时，汽轮机出力和循环水泵耗功同时发生改变，因此在分析凝汽器最佳真空的计算过程中，选取公式(21)作为目标函数，当目标函数取得最大值时，便可得到机组的最佳运行真空和泵的最佳转速。

fitness ΔNnet=ΔPtb-ΔPf

=(Ptb1-Ptb0)-(Pf1-Pf0)

(21)

式中 ΔNnet——机组的净功率增量；ΔPtb——汽轮机功率增量；ΔPf——循环水泵耗功增量；Ptb0——参考工况下机组功率；Ptb1——变工况后机组功率；Pf0——额定工况下循环水泵耗功；Pf1——变工况后循环水泵耗功。

通过前面的分析可知，在计算机组最佳真空的过程中，需同时对汽轮机末级、凝汽器换热以及变频循环水泵进行变工况计算，由于其之间相互影响且相互关系，任何一个系统参数的改变将会导致参数的重新分布，因此在变工况计算过程中，需进行反复迭代计算，直至汽轮机末级排汽量和排汽焓收敛为止，其计算流程如图3所示[11]。

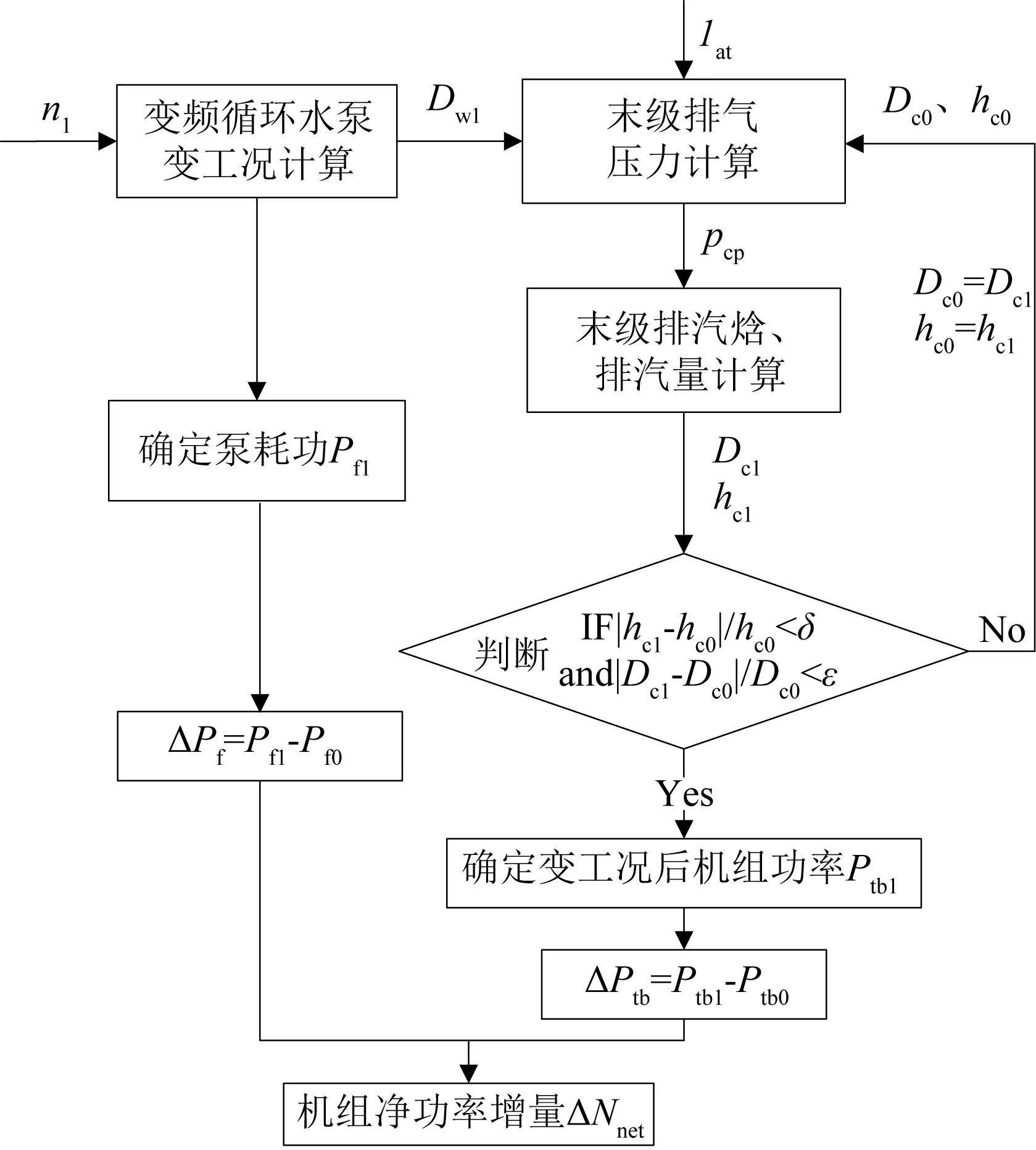
图3 最佳真空寻优计算流程

通过改变变频频率来改变循环水泵转速来寻找机组的最佳真空，在寻优过程中受到变频器有效调节范围和机组真空安全范围的限值。对于本文所研究的机组，其约束条件可以表示为

(1)pc∈[pcmin，pcmax]；(2)n∈[0.8nd，nd]。

其中：pcmin、pcmax分别表示为机组极限背压和最高允许背压，安全运行区间为[3.5 kPa 15 kPa]；nd表示机组循环水泵的额定转速，495 r/min。

3.2仿真验证

本文选取华能瑞金电厂350 MW超超临界机组作为研究对象，机组额定背压为5.7 kPa，极限背压为3.5 kPa，循环水泵额定转速为495 r/min。

参考工况A：机组功率350 MW；背压5.7 kPa；末级排汽量588.44 t/h；排汽焓值2 332.93 kJ/kg；水泵转速495 r/min；环境温度15℃。从关系曲线图4、图5中可以看出，在参考工况A下，循泵保持在额定转速495 r/min下时，机组效率最高。

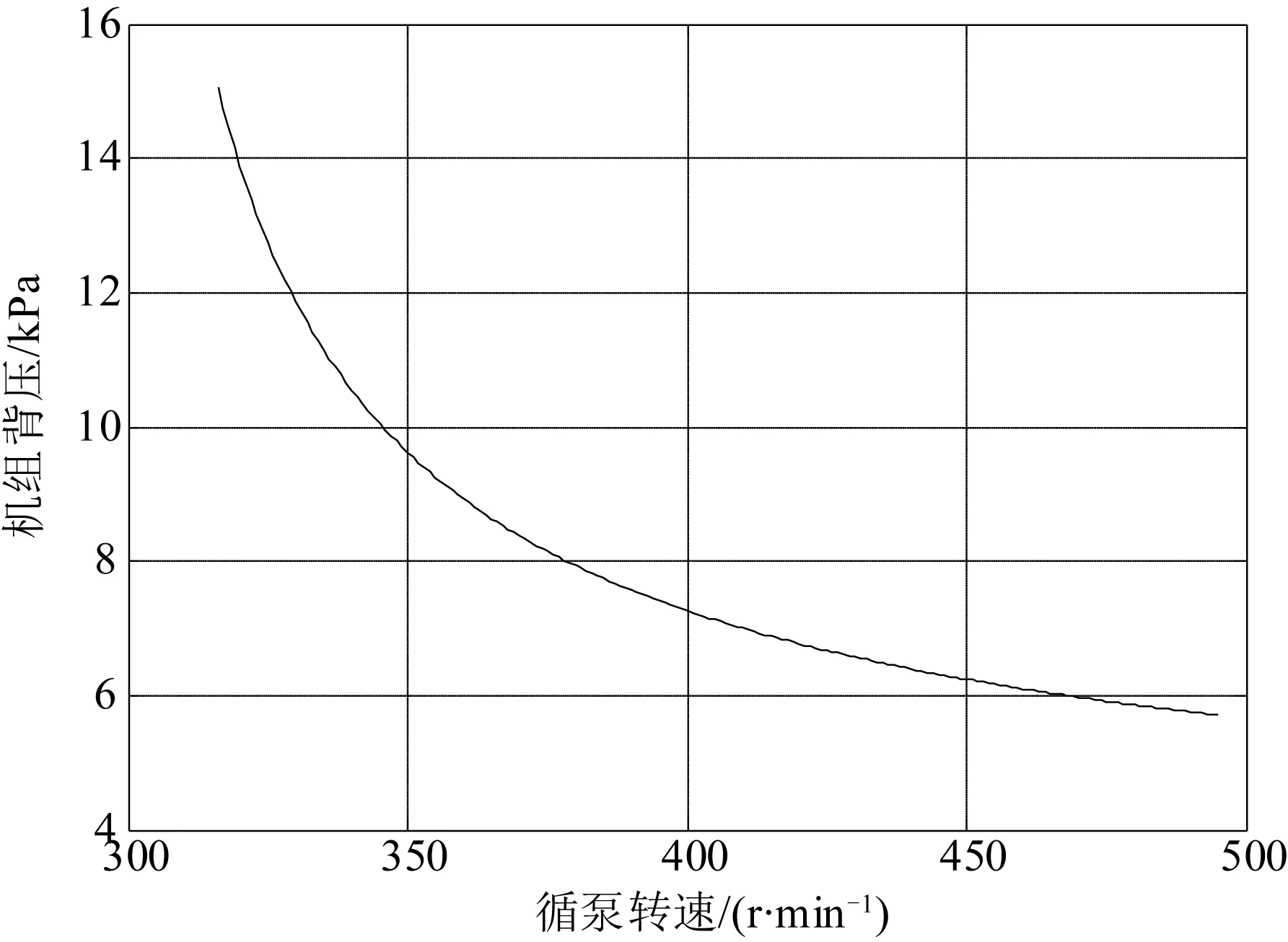
图4 循环水泵转速与凝汽器压力关系曲线

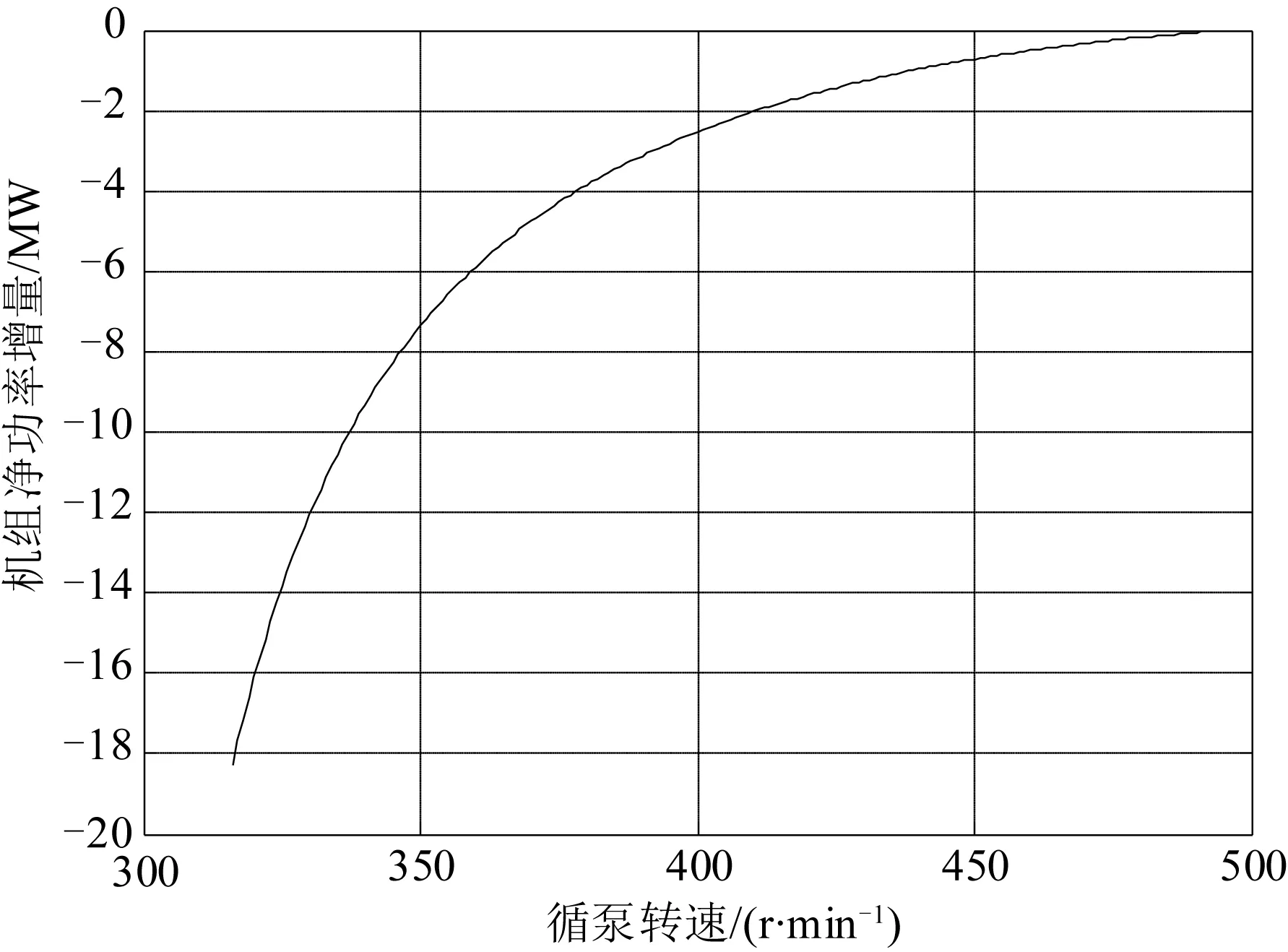
图5 循环水泵转速与净功率增量关系曲线

参考工况B：机组功率262.5 MW；背压5.7 kPa；末级排汽量448.53 t/h；排汽焓值2 365.0 kJ/kg；水泵转速495 r/min；环境温度25℃。表1为75%负荷下不同环境温度下机组最佳背压。

表1 75%负荷下不同环境温度下机组最佳背压

参考工况C：机组功率175 MW；背压5.7 kPa；末级排汽量315.47 t/h；排汽焓值2 419.7 kJ/kg；水泵转速495 r/min。表2为50%负荷下不同环境温度下的机组最佳背压。

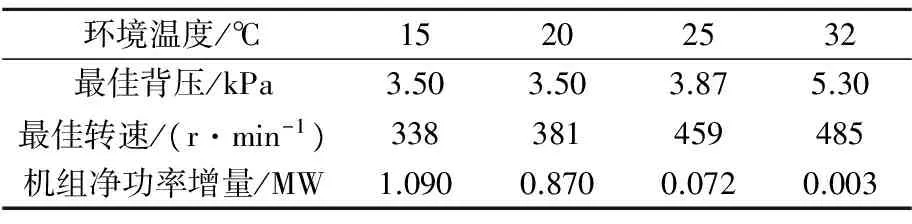
表2 50%负荷下不同环境温度下机组最佳背压

从3个参考工况的分析结果中可以看出，在高负荷工况下为了保持机组较高的真空，循环水泵一般维持在额定转速，而且此时机组的效率也最高；在低负荷工况下，特别在春、秋、冬季时环境温度较低，如果循环水泵仍保持在额定转速下运行，此时机组背压已达到其极限背压，造成资源浪费。此时通过变频循环水泵对机组循环水流量进行调节，可以有效地降低循泵的厂耗电量，提升机组的经济性。

3.3实时闭环优化控制系统

通过汽轮机冷端系统稳态计算模型，利用MODBUS/TCP方式实时获取模型计算中所需的运行数据，通过外接优化控制站对最佳真空进行实时计算，从而以最佳真空作为控制目标，实现对汽轮机冷端系统的实时闭环控制。

最佳真空实时闭环控制系统主要由以下3部分组成：

(1) 最佳真空计算模块。通过MODBUS/TCP的通信模式从机组DCS中获取需要计算的关键参数，通过最佳真空计算模块进行寻优计算，并将最终的变频器控制指令传送至系统DCS中。

(2) 优化定值投入允许逻辑。主要用于判断当前机组是否处于稳定工况，作为判断优化计算结果是否合理的依据，当机组处于变工况过程中利用实时稳态计算模型的计算结果将会偏离，因此只有当机组处于稳定工况时计算结果才合理可信，才可以作为最优设定值进行闭环控制。

(3)系统保护逻辑模块。系统保护逻辑由两部分组成：变频调节手/自动投入模块和逻辑保护解除模块。其中，逻辑保护解除模块主要考虑到系统的运行安全、机组的运行工况以及作为优化计算输入点的品质判断，当凝汽器真空、变频器电流超出限值时，则切除自动运行模式；当关键信号输入点出现坏品质时，则切除自动运行模式；当优化站心跳线信号消失时，则切除自动运行模式。

4 结语

为了提高火电机组的运行经济性，实现对汽轮机冷端系统的实时闭环优化控制，本文在分析汽轮机冷端系统运行机理的基础上，通过对冷端系统稳态计算模型的推导和分析，给出了火电机组冷端系统最佳真空控制运行方案。从优化结果中可以看出，通过汽轮机冷端系统最佳真空的连续调节，可以有效的改善机组的经济效益，提高机组的运行水平。

[1] HE W F, DAIY P, WANG J F, et al. Performance prediction of an air-cooled steam condenser using UDF method[J]. Applied Thermal Engineering, 2013, 50(1): 1339-1350.

[2]ZHAO H, WU H, CAO L. Analysis on the back-pressure optimum operation of the direct air-cooled condenser[C]. Power and Energy Engineering Conference (APPEEC), 2011 Asia-Pacific. IEEE, 2011: 1-4.

[3]王玮, 曾德良, 杨婷婷, 等. 基于凝汽器压力估计算法的循环水泵最优运行[J]. 中国电机工程学报, 2010,30(14): 7-12.

WANG Wei, ZENG Deliang, YANG Tingting, et al. The optimal running of circulating water pumps based on estimated condenser pressure[J]. Proceedings of the CSEE，2010，30(14)：7-12.

[4]闫顺林, 张春发，李永华，等. 火电机组热力系统汽水分布通用矩阵方程[J]. 中国电机工程学报, 2000,20(8):69-73,78.

YAN Shunlin, ZHANG Chunfa, LI Yonghua, et al. The steam-water distribution general matrix equation of thermal system for the coal-fired power unit[J].Proceedings of the CSEE,2000,20(8):69-73,78.

[5]张春发, 张素香, 崔映红, 等. 现行电力系统热经济性状态方程[J]. 工程热物理学报, 2001, 22(6): 665-667.

ZHANG Chunfa, ZHANG Suxiang, CUI Yinghong, et al. Thermo-economy state equation of modern power system[J].Journal of Engineering Thermophysics,2001,22(6):665-667

[6]周兰欣, 杨靖, 杨祥良. 300MW直接空冷机组变工况特性[J]. 中国电机工程学报, 2007, 27(17): 78-82.

ZHOU Lanxin,YANG Jing,YANG Xiangliang. Study on variable condition features for 300mw direct air- cooling unit[J].Proceedings of the CSEE,2007,27(17):78-82.

[7]杜小泽, 杨立军, 金衍胜, 等. 火电站直接空冷凝汽器传热系数实验关联式[J]. 中国电机工程学报, 2008, 28(14): 32-37.

DU Xiaoze, YANG Lijun, JIN Yansheng, et al. Development of experimental correlation for heat transfer coefficient of direct air-cooled condenser in power plant[J]. Proceedings of the CSEE,2008,28(14):32-37.

[8]杨立军, 杜小泽, 杨勇平, 等. 直接空冷系统轴流风机群运行特性分析[J]. 中国电机工程学报, 2009, 29(20): 1-5.

[9]YANG Linjun, DU Xiaoze, YANG Yongping. Wind effect on the thermo-flow performances and its decay characteristics for air-cooled condensers in a power plant[J]. International Journal of Thermal Sciences, 2012, 53: 175-187.

[10]胡勇. 闭式循环水系统的优化调度[D]. 北京: 华北电力大学, 2008.

[11]胡勇. 基于汽轮机蓄能特性的大型火电机组快速变负荷控制研究[D]. 北京: 华北电力大学, 2015.

(本文编辑：严 加)

Closed-Loop Optimization Control of Turbine Cold End System Based on the Real-Time Steady-State Model

LI Jianping1, LV Haitao1, ZHANG Jianzhong1, LI Hua1, HU Yong2, ZHONG Yiqing2, WANG Jianzhao2, WANG Baomin2

(1.Huaneng Ruijin Power Generation Co., Ltd., Ruijin 341108, China; 2. China Huaneng Group Clean Energy Technology Research Institute Co., Ltd., Beijing 102209, China)

The cold end system of the steam turbine is an important auxiliary system for the thermal power unit, and its operation condition is directly related to the safe and economical operation of the unit. This paper analyzes the heat transfer mechanism of steam turbine cold end system, and establishes the optimal vacuum steam steady-state calculation model for turbine cold end system through analyzing the turbine final-phase off-design condition calculation model, condenser heat transfer off-design condition calculation model and variable frequency circulating pump off-design condition features. It also analyzes the optimal vacuum for unit operation under different boundary conditions, then formulates the optimal vacuum closed-loop optimization real-time control system based by using steady-state calculation model, realizing the continuous adjustment of unit circulating cooling water flow rate, and improving the unit operation efficiency.

cold end system; optimum vacuum; circulating pump frequency conversion; closed-loop optimization

10.11973/dlyny201704027

TK26

：A

：2095-1256(2017)04-0472-06

2017-03-23