一种基于抛物线霍夫变换的雷达信号分选方法

曾德国，张 君，郑子扬，陈歆炜，徐富元

(中国航天科工集团8511研究所，江苏 南京 210007)

·技术前沿·

一种基于抛物线霍夫变换的雷达信号分选方法

曾德国，张 君，郑子扬，陈歆炜，徐富元

(中国航天科工集团8511研究所，江苏 南京 210007)

在雷达信号分选时，一般的思路是采用到达时间、脉宽、频率、到达方向等参数对信号进行分选，分选完成后再将同一辐射源的脉冲幅度提取出来，进行雷达扫描特性等分析。对某实际采集数据进行了分析，发现信号的时间、幅度曲线有明显的规律，采用了抛物线霍夫变换提取了全脉冲的幅度特性，并采用时间、幅度联合分析完成了信号的分选。仿真结果表明了该方法的有效性，为雷达信号分选提供了一条新的思路。

雷达；信号分选；抛物线

0 引言

雷达信号分选是电子侦察信号处理的关键技术，其主要功能是从电子侦察接收机形成的交错的脉冲描述字(PDW)流中分离出来自同一辐射源的脉冲信号序列，继而进行辐射源识别。雷达信号分选一般包括预处理及主处理，预处理的主要功能包括删除无用数据、区分已知雷达辐射源数据、利用先验信息检测和识别可能存在的雷达辐射源。主处理的主要目的是从预处理分选后输出的已知和未知辐射源数据中，利用尚未使用的脉冲重复间隔(PRI)及其它参数特征，进一步分选出每一部雷达的PDW序列，进行辐射源检测。预处理一般使用的参数包括来波方向、频率、脉宽、脉内调制特征等参数，一般不包含幅度特征；主处理主要使用的参数是信号到达时间，利用信号到达时间提取PRI以完成分选[1]。常规的信号分选是在提取属于同一部辐射源的雷达信息后，再提取其中的某项参数，完成来波方向及其变化、频率转移特性、脉宽转移特性、天线的扫描周期和扫描方式等物理特性的描述。在实际环境中，这种做法具有一定的通用性，即先根据受环境影响较小或者测量较为可靠的到达角度、频率、脉宽等参数，利用简单算法完成信号的筛选，然后再进一步利用复杂的PRI分析算法完成分选。然而，在某些环境中，电子侦察接收机可能不具备测向能力，且其接收的同一部雷达信号脉宽、频率甚至调制特性在脉冲之间都有可能变化，这将使得传统的预分选失效，增加了主分选处理的压力。

雷达波束扫描特性是电子侦察关心的一个重要特性，扫描一般分为机扫与电扫。对于机扫来说，一般有圆周扫描、扇形扫描和圆锥扫描三种基本类型，电子侦察方收到的雷达扫描波形脉冲间的幅度包络一般可认为是辛克函数[2]。通过对大量实际接收的雷达信号进行分析，发现也可以用抛物线函数近似表示幅度包络。本文在对某实际采集数据分析的基础上，将明显符合抛物线特性的PDW认定为同一部辐射源，完成了只利用雷达信号幅度、时间序列关系的信号分选，实现了在某些环境下预分选、主分选合一的雷达信号分选方法。

1 信号特性分析

某采集设备是单通道设备，没有测向功能，利用其完成了信号的中频采集。采集完成后，利用基于信道化原理的信号检测软件，完成了信号的检测，得到的脉冲幅度如图 1所示。

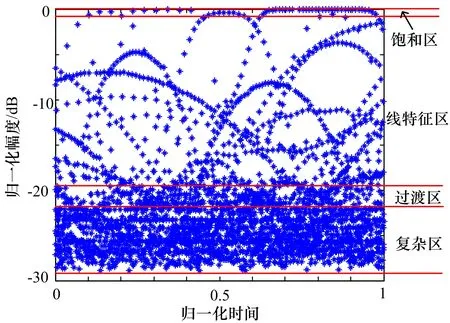
图1 接收机收到的脉冲时间、幅度关系图

从图 1可知，时间、幅度图上呈现了一些特性，可大致分为几个区：1)线特征区：时间、幅度呈现比较明显的抛物线特性，可以认为幅度符合抛物线特性分布的脉冲属于一部雷达；2)复杂区：在该区，信号能量较小，信号分布较为密集，已经不太容易从其中区分出具有明显时间、幅度分布特征的雷达；3)饱和区：线特征区往上，幅度在0dB附近时，信号饱和，抛物线被削顶，呈现出饱和特征；4)过渡区：在线特征区与复杂区之间，有些脉冲能够跟随线特征区的趋势，区分出线特征，剩余脉冲由于没有相关的趋势，不太容易区分线特征。根据不同区脉冲信号的不同特点，对于饱和区和线性特征区的雷达脉冲，可以利用脉冲的时间、幅度特征，实现信号的分离；对于过渡区的脉冲，可按线特征区的结果作为依据，进行部分脉冲的进一步分离；对于复杂区的脉冲，由于特征不太明显，不做区分。对于本次数据的相关特点，以dB为单位，将0～0.1定为饱和区，将-0.1～-18定为线特征区，将-18～-22定为过渡区，-22～-30定为复杂区。该区分只是一个初步区分，主要是为了给每个区有个初步的计算目标，尤其是线特征区、过渡区与复杂区的边界可以较为模糊。

每一个脉冲，可以描述为时间、幅度二维参数构成的全脉冲集合{PDWi}={ti,Ai,i=0,1,…,N-1}，其中，ti是脉冲到达时间，Ai是以dB为单位的脉冲幅度，N是脉冲个数。本文的时间全部按照最大时间进行了归一化，幅度按照最大的幅度也进行了归一化，且以dB为单位进行表示。把未处理的{PDWi}简记为{PDW0}。

1.1抛物线霍夫变换

从图1可知，线特征区有较为明显的抛物线特性。如何对这些抛物线进行检测、识别是首先面临的一个问题。可以采用卡尔曼滤波[3]、最小二乘[4]等方法实现抛物线的检测，但是这些方法存在需要起始航迹、多目标适应等方面的问题，在实际应用中有一定困难。霍夫变换[5]是一种有效的线检测方法，它将原空间全局范围内的有一定参数关系的元素进行聚类，在参数空间完成统计，实现线检测。由于霍夫变换在全局对所有可能的线统计，故在噪声中提取线具有较强的鲁棒性。本文从全局认知的角度，采用霍夫变换对抛物线进行检测。

令t={ti,i=0,1…,N-1}，则抛物线可描述为时间的抛物线函数，通用抛物线表达式可记为at2+bt+c，霍夫变换要完成的时间、幅度二维空间描述向抛物线的三维参数空间Pj1,j2,j3={aj1,bj2,cj3,j1=0,1,…,M1-1,j2=0,1,…,M2-1,j3=0,1,…,M3-1}转换，其中，M1、M2、M3分别为a、b、c的量化维度。由于3点就可以确定一个抛物线，因此，选取3个全脉冲即可得到1组抛物线参数Pj1,j2,j3，具体步骤如下：

步骤1参数初始化

取a、b、c参数空间单元大小分别为Δa、Δb、Δc，对抛物线参数空间进行参数化，得到三维空间参数Pj1,j2,j3，维度为M1×M2×M3，初始化Pj1,j2,j3空间计数三维矩阵Aj1,j2,j3=0,j1=0,1,…,M1-1,j2=0,1,…,M2-1,j3=0,1,…,M3-1。

步骤2 顺序样本组合采样、拟合及计数

按照排列组合取出三个点：从中按照排列组合的方式顺序取出三个脉冲{PDWi1,PDWi2,PDWi3}，其中要求：

(1)

式中，tth与Ath分别表示时间跨越门限及幅度差异门限。tth表示拟合的最长时间，其大小与适应的最大重复周期相关，本文取值0.1；Ath表示用于抛物线拟合的脉冲间的幅度差异极限，本文取5。

Aja,jb,jc=Aja,jb,jc+1

(2)

步骤3 抛物线确认

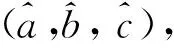
图2 抛物线重构曲线

1.2抛物线脉冲提取

步骤1脉冲粗提取

(3)

根据图2中确认的抛物线得出粗提取全脉冲，如图3所示。{PDW_Line}中包含了需要的、符合条件的大部分脉冲，下一步的目标是：1)将不符合条件的脉冲筛除；2)将符合条件，但不在{PDW_Line}中的全脉冲扩展进去。

步骤2 脉冲筛除

为了将不符合条件的脉冲筛除，首先估计{PDW_Line}的PRI，根据PRI对脉冲进行筛选，删除不符合条件的脉冲。图3中用圈标识的全脉冲即为不符合PRI条件的全脉冲，需要筛除。

图3 根据确认的抛物线粗提取全脉冲

此处采用多级直方图统计方法估计PRI。具体方法为：

(4)

式中，ti,ti-1来自于{PDW_Line}的时间序列，N1、N2、N3分别为直方图的等分数，在此分别取为10、100、1000，hist(·)为直方图统计函数，其输出x1、x2、x3为直方图横坐标及对应的统计样本数。

预设一定的抖动量p，找出符合下式的ti及ti-1，构成集合{PDW1}：

ti-ti-1≥(n-p)PRI

ti-ti-1≤(n+p)PRI

(5)

考虑到该批数据特点，本文取n=0,1,2,3,4,5。如此得出的脉冲可能包含脉冲到达时间比较接近的情况。对{PDW1}进行遍历，删除{PDW1}中到达时间≤pPRI的ti及ti-1，得到{PDW2}。

{PDW2}得到的脉冲描述字没有到达时间接近的情况，但是还是存在一定的概率，使得某些脉冲的幅度值与整个抛物线的趋势不太一致，也需要删除，在此，采用局部拟合的办法，对不符合抛物线规律的脉冲进行删除，具体的表达式为：

(6)

式中，M为邻近的点数，在此取3，polyfit(·)为抛物线拟合函数。

通过上述步骤，得到{PDW3}。

步骤3 脉冲扩展

通过步骤2的时间及幅度关系判断，可以认为剩下的全脉冲具有较为明确的抛物线及时间序列特性，但存在漏选的可能。本步骤是以这些全脉冲为基础，向着附近进行扩展，以期不要漏掉其它的全脉冲。

以{PDW3}的全脉冲为基础，判断{PDW0}内的全脉冲是否具备下式的条件，若具备，则认为属于扩展的对象，与{PDW3}合并，得到{PDW4}。

(7)

式中，ti∈{PDW0}，tq为{PDW3}中与ti时间距离最近的脉冲，tq″～tq″+2M+1∈{PDW3}且tq″～tq″+2M+1是与ti时间距离最近的2M+1个脉冲。得到{PDW4}后，从{PDW0}中剔除{PDW4}，重复1.1的步骤1，直到剩余脉冲小于一定的值，如5个。图4是扩展后得到的曲线。

图4 脉冲扩展后得到的曲线

1.3抛物线二次扩展及合并

步骤1二次扩展

在1.2步骤3中，脉冲扩展得到{PDW4}的是来自于线特征区，还可根据得到的{PDW4}对过渡区及复杂区的脉冲进行分辨，得到更长的脉冲扩展{PDW5}。

步骤2 多抛物线合并

对每次得到的{PDW5}进行合并，合并的准则是PRI一致，此处定义为PRI差别在5%以内，可以将几条抛物线进行合并，描述信号的特性。得到的典型结果如图5～7所示。

图5 跨饱和区与线特征区的抛物线特性全脉冲

图6 线特征区提取出的抛物线特性全脉冲

图7 两抛物线合并结果

图5的全脉冲跨了饱和区与线特征区，通过脉冲扩展，可以得到完整的脉冲。图6是一个正常的线特征区提取出的抛物线特性全脉冲。图7是多抛物线合并的结果，可以明显看出是由两个抛物线全脉冲合并所得。由于篇幅限制，在此未列出所有分选的结果。

2 结束语

本文针对实际采集数据，构造了一种利用抛物线霍夫变换提取全脉冲幅度的规律进行分选的方法，以期在某些复杂电磁环境下实现基于时间幅度的预分选、主分选合一的雷达信号分选方法。该方法通过霍夫变换，实现了全脉冲时间、幅度二维空间向抛物线三维参数空间的转换，实现了辐射源扫描特性的参数化表示，将信号分选问题转化为了参数检测问题。为了有效检测辐射源的抛物线扫描特性，通过粗提取、筛除、扩展三步完成了全脉冲的精细化操作，提高了信号分选的准确性。仿真结果表明了该算法针对该实际采集数据的有效性，与现有的实际分选算法相比，具有稳定性好的优势。

该算法还须进行改进、完善及大量测试，并与现有分选算法进行融合，以提高相关分选效能。而且，相扫雷达与本文研究的机扫雷达的扫描特性不尽一致，能否用抛物线对相扫雷达进行建模还有待进一步研究。最后，霍夫变换计算量较大，主要体现在“顺序样本组合采样、拟合及计数”，可以考虑采用随机霍夫变换等方法，通过减少迭代次数，提升算法的工程实用性。■

[1] 赵国庆. 雷达对抗原理[M]. 2版.西安：西安电子科技大学出版社, 2012: 95-100.

[2] 陈卓，史小伟，甘荣兵，等.一种基于短时间窗幅度变化的雷达扫描方式识别[J]. 电子信息对抗技术,2015,30(1):48-52.

[3] 闫小龙，陈国光，杨东. 抗野值卡尔曼滤波在火箭弹落点估计中的应用[J]. 弹箭与制导学报, 2016,36(3):94-98.

[4] 汤卫红，栾胜利，李良福. 光学图像中的抛物线目标特征检测方法研究[J].应用光学, 2013,34(4):609-613.

[5] Hough PVC. Method and means for recognizing complex patterns: US , 3069654 [P]. 1962-12-18.

A radar signal sorting method using parabola Hough transform

Zeng Deguo, Zhang Jun, Zheng Ziyang, Chen Xinwei, Xu Fuyuan

(No.8511 Research Institute of CASIC, Nanjing 210007, Jiangsu, China)

In radar signal sorting, the general idea is to use the time of arrival, pulse width, frequency, direction of arrival and other parameters of the

signal. After signal sorting, the amplitude of the same emitter is extracted to analyze the characteristics of radar scanning etc. The certain collected actual data is analyzed, and it is found that the time-amplitude curve had obvious regularity. The parabola Hough transform is used to extract the amplitude regularity of the pulse, and the combined analysis of the time and amplitude is adopted to complete signal sorting. Simulation results show the effectiveness of the presented method ,and a new idea for radar signal sorting is provided.

radar; signal sorting; parabola

2017-06-15;2017-07-25修回。

曾德国(1985-)，男，高工，博士，主要研究方向为电子对抗。

TN974

： A