SLSB-forest：高维数据的近似k近邻查询

钱途，钱江波，董一鸿，陈华辉

（宁波大学信息科学与工程学院，浙江 宁波 315211）

SLSB-forest：高维数据的近似k近邻查询

钱途，钱江波，董一鸿，陈华辉

（宁波大学信息科学与工程学院，浙江 宁波 315211）

近似 k近邻查询的研究一直受到广泛关注，局部敏感散列（LSH）是解决此问题的主流方法之一。LSH及目前大部分改进版本都会面临以下问题：数据散列以后在桶里分布不均匀；无法准确计算对应参数 k的查询范围建立索引。基于此，将支持动态数据索引的LSH和B-tree结合，构建新的SLSB-forest索引结构，使散列桶里的数据维持在一个合理的区间。针对SLSB-forest提出了两种查询算法：快速查找和准确率优先查找，并通过理论和实验证明查找过程中查询范围的动态变化。

近似k近邻；局部敏感散列；高维数据

1 引言

最近邻（nearest neighbor）查询问题在模式识别、数据挖掘等领域应用非常广泛，其目标是找出与查询点距离最近的点。高维空间下的最近邻问题一直受到广泛关注，特别是在音频、图像等领域。线性查找是处理近邻查询最直观的方法，但是开销会随着数据集的增大呈线性增长。传统基于空间划分法的树索引结构，如 R-tree[1]、SR-tree[2]、K-D tree[3]，在低维空间下可以高效地返回准确的近邻查找结果，但是这些索引的数据维度一旦超过10，就会产生维度灾难问题，其查询效率甚至不如线性查找[4]。

高维空间下的近邻查询很难提高效率，为此提出了近似近邻查询（c-approximate nearest neighbor search）。近似近邻查询返回的不是精确解，而是允许一定误差范围内的近似解。局部敏感散列（locality sensitive hash，LSH）[5]是目前高维空间下解决近似近邻查询问题最主流的方法。LSH基本思想是通过一系列具有位置敏感性质的散列函数，将高维空间下距离相近的数据点散列到相同的桶中。查询时，LSH将查询点散列到目标桶中，将此桶中的数据作为最终结果的候选集。为了提高查找准确率，通常会构建多个LSH索引，将各个索引的候选集合并，用线性搜索的方法查找候选集找出最近邻。

1998年，Indyk等人[5]第一次提出LSH理论，用以解决海明空间下的近似成员查询，经过近30年的发展，衍生了许多LSH变体。2004年，Datar等人[6]将 LSH扩展到欧氏空间，提出满足p-stable分布的散列函数E2LSH，E2LSH在欧氏空间下具有很好的位置敏感性，可以使空间中两个距离相近的点以较高的概率散列到同一个桶中。E2LSH在实际使用中需要大量的散列表才能达到较高的准确率，因此Lv等人[7]提出multi-probe LSH减小索引数量。multi-probe LSH通过衍生一个探测序列，在查询时不仅查询目标桶，同时也会根据探测序列查询邻近桶。基于熵（entroy-based）的LSH[8]通过基于熵的概念产生一些与查询点满足一定条件的虚拟点，将虚拟点所在桶号的点作为查询结果的候选集。为了减小LSH查询时庞大的I/O开销，SK-LSH[9]定义了一种新的衡量桶之间的距离，使得桶号像自然数一样有序。为了同时保证查询质量和查询效率，LSB-forest[10]将散列后的桶号处理成Z-order编码，对编码构建B-tree索引，LSB-forest查询时会优先寻找具有最长公共前缀长度（LLCP）的桶。MLBF[11]成功地将 LSH[12]和布隆滤波器（Bloom filter）[13]结合，并提出多粒度查询的概念。

将高维数据散列到低维的桶中，即使数据在原始空间均匀分布，数据散列后也会存在分布不均匀的问题，不同桶里的数据相差比例可高达几十倍。图1、图2分别是均匀数据集和真实数据集（ANN_SIFT1M）散列以后在桶里的分布情况。桶里数据分布不均匀会极大影响查询效率，因此胡海苗等人[14]提出了一种可扩展的索引SLSH解决桶里数据分布不均匀问题。SLSH主要针对（r,c）-近邻查询问题，对于近似最近邻问题，若查询近邻个数为k，无法计算出有效的查询范围r。本文将SLSH和B-tree相结合，提出了一种局部有序的SLSB树索引结构，通过建立多棵树构建SLSB森林（SLSB-forest）结构。针对近似最近邻问题给出了两种查询算法：适用于 k较小的快速查询和适用于 k较大的准确率优先查询，并且通过理论和实验证明这两种查询方法都可以动态地扩大查询半径，同时满足效率和准确率需求。

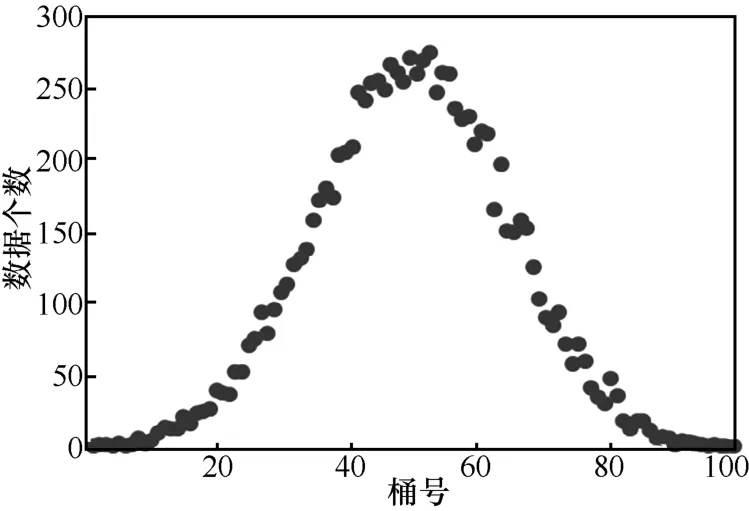
图1 均匀数据集分布情况

图2 ANN_SIFT1M数据集分布情况

2 基础知识

2.1 LSH

严格来说，LSH并不能直接解决近似k近邻查询（c-AkNN）问题。LSH最初设计是为了解决（r,c）-近邻查询问题。

定义1 （（r,c）-近邻查询）D是d维空间下的数据集，B(q,r)是以q为中心、r为半径的超球形范围。（r,c）-近邻查询问题需要返回以下结果。

· 如果超球空间B(q,r)至少包含D中的任意一点，则返回与查询点q距离小于cr的一个点。

· 如果B(q,cr)未覆盖D中的任意一点，则返回空。

定义2 （c-ANN查询与c-AkNN）D是d维空间下的数据集，对于查询点 q， o∗是数据集 D中距离q最近的点。c-ANN查询返回的结果o需要满足，其中c＞ 1。更一般化的 c-AkNN查询，如果需要查询的近似近邻个数k＞1时，近似k近邻的结果集，需要满足是查询点的真实k近邻。

图3是3个不同情况的（r,c）-近邻查询，如果现在需要支持c-AkNN查询，设k=10。可以看出，图3（a）设置的查询半径r刚好可以返回合适数量的查询结果；图3（b）查询范围内的数据只有2个，不能够返回足够数量的结果；图3（c）由于数据分布比较密集，在查询范围内的数据远远大于10，需要消耗更多额外的时间对候选集进行筛选。在实际的 c-AkNN查询时，由于数据分布不均匀且查询近邻 k不断变化，很难找到合适的r值。

定义3 （LSH[5]）给定查询范围r，比例参数 c( c＞0)，概率值p1、p2(p1＞p2)，o、q代表两个数据点，dist(⋅)是欧氏空间的距离度量函数。如果散列函数 h(⋅)能够满足以下条件：

则h(⋅)函数被认为是距离敏感的。本文采用参考文献[11]中适用于欧氏距离的局部敏感散列函数：

其中，a的每一维都是服从标准正态分布的，w是桶的宽度，b是区间(0,w)中的随机数。数据集中的任意两点o、q之间的距离是欧氏距离下的局部敏感散列函数。o、q通过散列以后发生碰撞的概率计算如下：

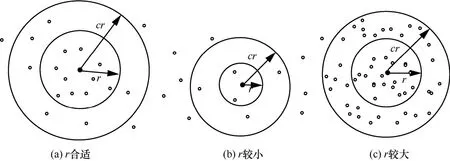
图3 （r,c）-近邻查询

为了更有效地解决欧氏空间下的（r,c）-近邻查询问题，会通过与（AND）和或（OR）操作增强LSH的查询准确率。与操作是随机生成t个LSH函数h1,…,ht，将这t个LSH函数组合构造成一个组合散列函数g(⋅)，对于任意数据o，其散列值为；或操作是通过构建多个索引，查询时分别查找各个索引并对结果进行整合，以提高查询的准确率。

2.2 高维动态数据索引SLSH

SLSH是一种动态可扩展的散列算法，主要针对分布不均匀的数据集设计的散列表结构。单个散列表的散列函数为w是每个 h(⋅)函数对应的桶宽且满足构建散列表的过程中并不是同时计算的，先由对数据第一次散列，如果桶里的数据个数大于给定阈值 N，对桶里的数据用下一个更细区分度的散列函数进行散列，依次类推，直到桶里的数据个数小于 N或者计算到第t个为止。

SLSH是用来解决不均匀数据集上（r,c）-近邻查询问题，对于c-AkNN查询问题，SLSH会遇到和传统LSH相似的问题。如果将查询半径r设置为查询点和最近邻的距离，SLSH的效率会很高，但是找到相应的查询半径十分困难。即使找到对应的r，不同查询任务的r也会发生变化。

3 SLSB-forest

SLSH通过逐层散列的方法对数据集进行散列，数据分布稀疏的区域用较大的桶切分，数据分布密集的区域用更细的桶进行划分。若要使SLSH支持多种近邻查询，必要的方法是对数据进行较细的划分，在查询时如果候选点个数小于k，通过合并相邻桶里的点直到候选点个数大于k。

定义4（桶距度量）桶号由多个散列函数的散列值组合而成，单个散列表的散列函数为查询点q的桶号为，定义桶号之间的距离。本文后半部分还需要比较每一层散列函数的桶距，表示为，第i层的桶距

与q桶号距离小于或等于Δ的桶，满足条件

SLSH无法快速地查找相邻桶，因为其算法未保存空间位置信息。常见的空间索引如R-tree因插入等操作较为繁琐，效率也不高，因此提出了将SLSH和B-tree相结合的索引结构，使索引结构局部有序，在查找时可同时在不同层次的索引检索，可以加速查找相邻桶。

3.1 SLSB-tree构建

SLSB-tree使用欧氏空间下的E2LSH函数，单个散列表的散列函数为，单个散列桶最多存放N个数据。SLSB-tree是逐层构建的，首先将数据集D中的数据通过 h1(⋅)进行第一层散列，散列后的第一层桶号是一维的，可以快速地对第一层桶号构建B-tree索引使桶号按顺序依次排列。在散列过程中，如果某一桶里的数据个数大于阈值 N，将这个桶标记为超桶，并对超桶里的数据用下一级散列函数即 h2(⋅)进行第二次散列。超桶里数据散列以后的桶号需要构建一个新的次级B-tree索引，超桶存放的不再是数据，而是一个新的小型B-tree索引。如果第二层中仍有数据个数大于N的桶，将这个桶标记为超桶并重复上述处理超桶的步骤直到无超桶出现或散列到第t层为止。SLSB-tree构建完成后除第一层的桶号是全局有序外，其他层只在相应的超桶下是有序的，相同层次不同超桶之间不存在顺序关系。SLSB-tree查找查询点对应的目标桶时，先计算第一层散列值，如果对应的第一层桶是超桶，计算下一层散列值并查找超桶下的索引，直到查询到非超桶为止。

算法1 创建SLSB-tree

输入：D (数据集), q (查询点), t (Hash函数个数), N(单个桶最大存储数据个数)

单个SLSB-tree会伴随很高的假阴性，假阴性指相近的数据没有落入同一个桶中，所以通过构造多个SLSB-tree形成SLSB-forest，查询时同时在所有树上进行查询并对候选集合并，可以显著地提高准确率。

SLSB-forest结构如图4所示，tree 1和tree L是两棵已经建好的SLSB-tree，第一层为 h1(⋅)散列后的桶号按顺序相邻。tree 1和tree L中超桶分别是5、9和6、7，用深色桶标记，超桶下对应的是一个新的B-tree索引。以tree 1为例进行查询目标桶{5,7}，在第一层时找到桶{5}时遇到超桶，需要在{5}对应的索引下寻找第二层索引桶{7}。

SLSB-tree的关键是快速寻找相邻桶，如果桶号是一维的，即散列函数，可以由查询点向外侧依次查找相邻桶，但是没有与操作的LSH假阳性会很高。SLSB-tree除第一层之外的其他桶只是局部有序，每次寻找最近桶会在查找过程中消耗一些额外时间，考虑到近似近邻查找只需满足一定的近似比例，所以提出了两种查询方法：快速查找和准确率优先查找。

3.2 快速查找

快速查找的思想是每次向两侧寻找的桶不必是最近桶，只需要桶距小于给定的阈值。SLSB-tree每一层的桶号都是局部有序，即在同一个超桶下的所有桶是顺序排列。快速查找算法如下：查询桶号为，位于第i层索引。查询时如果需要查找邻近桶，只需从q桶号向左右两侧顺序选择距离最近的桶查询，向两侧查找有3个终止条件：①候选点个数大于k；②同一超桶下的桶都已查询；③当前索引中没有满足的桶，Δi是当前索引层允许向两侧寻找的最大距离，每一层对应一个Δi，计算方式在第4节给出。遇到终止条件①，直接跳出查询；遇到终止条件②和③，需要返回第（i-1）层索引，从向外侧查找最近桶。如果在第（i-1）层遇到其他超桶，需要在超桶对应的下一层索引中查找，查找相邻桶的方法和上述一致。

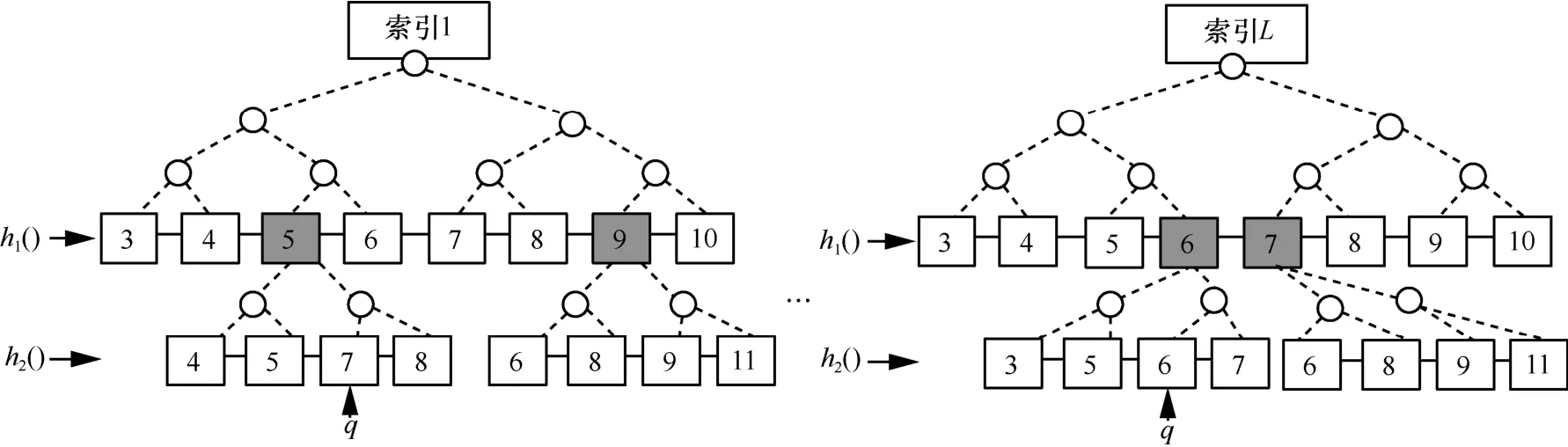
图4 SLSB-forest结构

3.3 准确率优先查找

快速查找是不断地向两侧查找满足一定条件的桶，如果向外查询每次都能查询最近的桶，准确率会更高。准确率优先查找算法如下。

遍历候选桶队列时，按顺序计算候选桶与查询桶的距离是否等于1，若不等于，跳过；若等于，需要分两种情况。如果该桶是非超桶，则加入结果集并在队列中将其删除，并加入未遍历的相邻桶至候选队列中；如果是超桶，超桶对应的索引按照 SLSB-tree查询Δ=0的方法查询，删除此桶并加入未遍历的相邻桶。当候选队列遍历结束，仍需查找更多相邻桶，从头开始再次遍历候选队列查找桶距为Δ+1的桶。

以图4 tree L为例，图5展示了准确率优先查询的过程。查询点q的桶号{6,6}，查询Δ=0时经过桶{6}、{6,6}，将候选桶{5}、{7}和{6,5}、{6, 7}加入候选桶队列中。当需要查找Δ=1的相邻桶时，仅需计算队列中的桶号和查询桶号的距离，满足Δ=1的桶为{5}、{7}、{6,5}、{6, 7}，将其中的非超桶直接加入结果集中，并将它们未查询过的相邻桶{4}、{8 }、{6, 3}加入候选队列。对于超桶{7}，在其对应的索引中查找与查询桶在第二层索引相同的桶号即{7,6}加入结果集，查询路径过程中的邻近且未查询过的桶{7,8 }加入候选队列中。若继续查询Δ=2，队列中只有{4}、{8}两个桶满足，重复Δ=1时的查询操作直到找到足够的近邻。

图5 准确率优先查询的过程

4 理论证明

本节将对SLSB-forest进行理论分析，主要针对以下两个问题：两种查找方法在查询过程中查询范围的变化和快速查找过程中每一层Δi的计算。

本文采用的是欧氏空间下的局部敏感散列，设桶宽为w，查询半径为r，近似比例为c。根据式（1）可以得出碰撞概率的计算式为：

其中，norm()是标准正态分布的累积分布函数，可以分别求出散列函数为，则在单个散列表中距离r的碰撞概率为。

4.1 准确率优先查询范围变化

准确率优先查询的原理是增大桶宽扩大查询范围，在寻找桶距为0、1、2…时，对应的桶宽为w、3w、5w…，若桶距为Δ，对应的散列函数桶宽为（ 2Δ+1)w。此处的桶宽（ 2Δ+1)w和直接设置散列函数的桶宽有明显区别，因为目标桶一直在宽为（ 2Δ+1)w桶的中央，碰撞概率的计算方式会有所改变。其计算方式如下：

查找相邻桶的概率计算如图6所示，通过随机生成距离为[1,180]的点，每一个整数距离生成1 000对数据，设置桶宽w=50，通过实验来模拟解碰撞概率。图6中平滑的曲线表示通过计算式计算的概率，波动的曲线表示实验计算的概率。从图6可以看出，实验计算的不同Δ的碰撞概率和通过公式计算的概率吻合，由此验证了理论推导的正确性。

图6 查找相邻桶的概率计算

准确率优先查询范围变化如图7所示，设近似比例 c=2，根据式（5）计算不同距离r在 Δ= 1、 2、 3时查询范围的变化情况。由于向两侧查找会使距离较近的桶碰撞概率显著升高，但是随着r的增大，范围扩大比例逐渐趋于平缓，并且α= β≈2Δ+ 1。

图7 准确率优先查询范围变化

4.2 快速查询范围变化

快速查询的本质是通过减小g(⋅)中散列函数的个数t达到扩大查询范围的目的。查询桶在第i层查询，若需要返回上一层（i-1）层查询时，在第i层查询的桶可以合并为一个大桶。若g(⋅)散列函数个数由t变为，假设查询范围扩大为α，需满足通过求解方程：

可以求出t发生变化后对应的查询范围。图8是不同距离下快速查询范围的变化情况，原始查询t=6，近似比例c=2，从图8可以看出，α、 β随着查询范围 r的增大在一开始会有一小段下降，随后一直上升，当 t=4时更加明显，且β的上升速度明显要高于α。

图8 快速查询范围变化

4.3 范围变化对效率的影响

查询范围(r, c)的变化会直接影响查询效率。设通过查询相邻桶查询范围扩大为(αr ,βc)，最理想的情况是α= β=1，但是此过程必定会使查询范围变大，所以希望α、 β尽可能小。不考虑r特别小的极端情况，快速查询和准确率优先查询相比，查询同样多的相邻桶，α快速＜α准确，但是，尤其当r较大时，β快速将远远大于α快速。

α较小可以使查询质量更高，但是若β远大于α，会使假阳性增大，所以快速查询在查询近邻个数较少或数据较密集时准确率较高，因为其对应的查询范围 r较小。当数据稀疏或者查询近邻个数较大时，适合使用准确率优先查询，因为当r越大时，α、 β不会随着r发生明显变化。

4.4 快速查找{Δ1,…, Δ2}的计算

设置每一层Δi的意义在于在当前子索引中继续向外侧寻找相邻桶不会使准确率发生明显变化，停止当前索引查找，返回上一层索引查询相邻桶。根据式（4）可以求出查询到第i层索引对应的查询范围(αir ,βic)。在第i层查询桶号满足到查询桶号满足的桶，距离为αir 的点碰撞概率变化为：

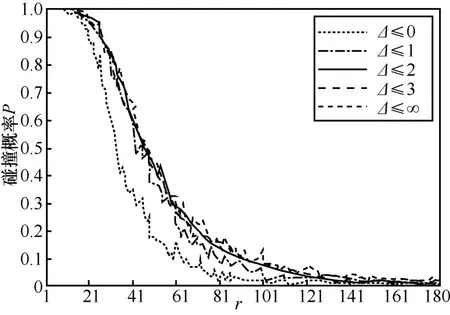
图9 快速查询碰撞概率变化

5 实验分析

本文实验环境的CPU为Intel Core i7-6500U、8 GB DDR3内存，分别在3个真实数据集上进行测试，利用Java实现了SLSB-forest算法，并和传统LSH、LSB-forest、C2LSH进行对比。

5.1 实验数据集

Mnist[10]：包含60 000个手写数字图像的训练集，每一图像由28 dpi×28 dpi个像素点构成，相当于一个784维的高维数据。Mnist还包含一个大小为10 000的测试集，从中抽取1 000个作为查询对象。

Color[10]：包含68 040个32维的数据，其中每一个点都来自 Color数据集中的图片颜色直方图。从数据集中随机抽取1 000个点作为查询集，并从Color中删除，查询集大小为1 000，数据集大小为67 040。

ANN_SIFT1M[12]：包含 100万条 128维的SIFT特征集以及大小为1万条的查询特征集。

5.2 性能评估

通过对比算法的查询结果质量和查询时间开销来评估SLSB-forest的好坏。

准确率（Ratio）：评估近似近邻查询结果的准确性。查询点q的k近邻真实结果为…，近似近邻查询结果为 o1,…,ok。对于任意i∈[1,k]，定义rank- i近似比例为rank-i是衡量第i个查询结果的近似比例，对于整个结果的近似比例计算方式为Ratio=，Ratio越接近1代表查询结果越接近准确结果。

平均查询时间（ART）：查询时间主要分为桶查询和候选集筛选两部分。桶查询包括目标桶查找和相邻桶查找，若查询的近邻数量 k较小，桶查询对平均查询时间的影响较大；若 k较大，候选集筛选占平均查询时间的比重很大。

5.3 实验比较

通过查询近邻个数k的变化来对比5种查询方法的性能。k的增加意味着查询范围需不断扩大，实现传统LSH算法时，通过实验寻找较合适的参数以适应多种k查询。图10和图11分别是Mnist和 Color数据集上的准确率比较，由图 10和图11可以看出，SLSB-forest的准确率相对于其他 3种算法都有很大的提升。Color数据集上，C2LSH在k比较小时准确率较高，接近SLSB快速查询的效率，但是随着k的增大，SLSB的两种查询算法准确率呈下降趋势，C2LSH呈上升趋势且一直高于SLSB算法。快速查找的准确率在k较小时，比准确率优先查找要低。随着k的增大，准确率优先查询的结果相比快速查询更接近真实结果。

图12和图13是查询时间的比较，可以看出4种查询方法中最快的还是直接用LSH。本文实验中使用的 LSH是经过多次调试寻找的较高效的参数，所以查询速度较高。LSB-forest在 Color数据集上的查询速度较快，但是LSB-forest要达到较高的准确率一般需要建立20棵以上的树，所以在相同准确率的前提下SLSB-forest更具有优势。C2LSH在两个数据集上的查询速度均快于SLSB，但是和SLSB的快速查找算法相比优势并不明显。快速查询相比准确率优先查询速度更快，尤其在 Color数据集中。

图10 Mnist数据集上的准确率比较

图11 Color数据集上的准确率比较

图12 Mnist数据集上的查询时间比较

图13 Color数据集上的查询时间比较

快速查询和准确率优先因为其动态扩展查询范围的方式不一样，在合并多个索引时候选集的数量也会有明显区别。图14是未合并前多个索引候选集的数量和，未合并是指没有去除重复的候选集。图15是合并之后的候选集数量，在未合并之前两种查询方法的候选集数量几乎相同，但是合并之后准确率优先的候选集数量有一个明显的下降，并且随着k的增大下降得越明显。其主要原因是快速查询的β会随着k的增大而远远大于α，假阳性明显增高，而准确率优先α =β。如果查询近邻个数较多时，则优先采用准确率优先查找，因为其可以减少筛选候选集所消耗的时间。

图14 未合并前多个索引候选集的数量和

6 结束语

针对LSH桶里数据分布不均匀的问题[15]，提出SLSB-forest算法和两种能够动态扩大查询范围的查询方法：速度优先和准确率优先。速度优先通过减小与操作的散列函数个数动态扩大查询范围，而准确率优先则通过扩大桶宽动态扩大查询范围，理论和实验证明了两种查询方法的范围动态变化，并分析了两种查询方法的利弊。速度优先适合近邻个数 k较小或数据较密集的情况，此时查询范围较小；准确率优选适用于数据稀疏或者k较大的情况，此时查询范围会较大。

图15 合并之后的候选集数量

[1] GUTTMAN A. R-trees: a dynamic index structure for spatial searching[J]. ACM SIGMOD Record, 1984, 14(2): 47-57.

[2] KATAYAMA N, SATOH S. The SR-tree: an index structure for high-dimensional nearest neighbor queries[C]//ACM SIGMOD International Conference on Management of Data, May 11-15, 1997, Tucson, Arizona, USA. New York: ACM Press, 1997: 369-380.

[3] 过洁, 徐晓旸, 潘金贵. 虚拟场景的一种快速优化 Kd-Tree构造方法[J]. 电子学报, 2011, 39(8): 1811-1817. GUO J, XU X Y, PAN J G. Build Kd-Tree for virtual scenes in a fast and optimal way[J]. Chinese Journal of Electronics, 2011, 39(8): 1811-1817.

[4] WEBER R, SCHEK H J, BLOTT S. A quantitative analysis and performance study for similarity-search methods in high-dimensional spaces[C]//International Conference on Very Large Data Bases, August 24-27, 1998, San Francisco, CA, USA. New York: ACM Press, 1998: 194-205.

[5] INDYK P, MOTWANI R. Approximate nearest neighbors: towards removing the curse of dimensionality[J]. Theory of Computing, 2000, 604-613(11): 604-613.

[6] DATAR M, IMMORLICA N, INDYK P, et al. Locality-sensitive hashing scheme based on p-stable distributions[C]//Twentieth Symposium on Computational Geometry, June 8-11, 2004, Brooklyn, New York, USA. New York: ACM Press, 2004: 253-262.

[7] LV Q, JOSEPHSON W, WANG Z, et al. Multi-probe LSH: efficient indexing for high-dimensional similarity search[C]// International Conference on Very Large Data Bases, September 23-27, 2007, Vienna, Austria. New York: ACM Press, 2007: 950-961.

[8] PANIGRAHY R. Entropy based nearest neighbor search in high dimensions[C]//The Seventeenth Annual ACM-SIAM Symposium on Discrete Algorithms, November 4, 2005, Miami, Florida, USA. [S.l.:s.n.], 2005: 1186-1195.

[9] LIU Y F, CUI J T, HUANG Z, et al. SK-LSH: an efficient index structure for approximate nearest neighbor search[J]. Proceedings of the VLDB, 2014, 7(9): 745-756.

[10] TAO Y F, YI K, SHENG C, et al. Quality and efficiency in high dimensional nearest neighbor search[C]// ACM Sigmod International Conference on Management of Data, June 29-July 2, 2009, Providence, Rhode Island, USA. New York: ACM Press, 2009: 563-576.

[11] QIAN J, ZHU Q, CHEN H. Multi-granularity locality-sensitive bloom filter[J]. IEEE Transactions on Computers, 2015, 64(12): 3500-3514.

[12] PAULEV L, GOU H, AMSALEG L. Locality sensitive hashing: a comparison of hash function types and querying mechanisms[J]. Pattern Recognition Letters, 2010, 31(11): 1348-1358.

[13] QIAN J, ZHU Q, WANG Y. Bloom filter based associative deletion[J]. IEEE Transactions on Parallel and Distributed Systems, 2014, 24(8): 1986-1998.

[14] 胡海苗, 姜帆. 基于可扩展LSH的高维动态数据索引[J]. 软件学报, 2015, 26(2): 228-238. HU H M, JIANG F. Scalable locality sensitive hashing scheme for dynamic high-dimension data indexing[J]. Journal of Software, 2015, 26(2): 228-238.

[15] 吴军. 大数据和机器智能对未来社会的影响[J]. 电信科学, 2015, 31(2): 7-16. WU J. Big data, machine intelligence and their impacts to the future world[J]. Telecommunications Science, 2015, 31(2): 7-16.

SLSB-forest: approximate k nearest neighbors searching on high dimensional data

QIAN Tu, QIAN Jiangbo, DONG Yihong, CHEN Huahui
College of Information Science and Engineering, Ningbo University, Ningbo 315211, China

The study of approximate k nearest neighbors query has attracted broad attention. Local sensitive hash is one of the mainstream ways to solve this problem. Local sensitive hash and its varients have noted the following problems: the uneven distribution of hashed data in the buckets, it cannot calculate the appropriate query range (for the parameter k) to build index. To tackle the above problem, a new data struct which called SLSB-forest was presented. The SLSB-forest combined the LSH and the B-tree to maintain the amount of bucket’s data in reasonable range. Two query algorithms were proposed: fast and accurate priority search. Theory and experimental results prove that query range can dynamic change during searching approximate k nearest neighbors.

approximate k nearest neighbor, locality sensitive hash, high dimensionality

TP311

：A

10.11959/j.issn.1000-0801.2017193

钱途（1992-），男，宁波大学信息科学与工程学院硕士生，主要研究方向为大数据、数据挖掘。

钱江波（1974-），男，博士，宁波大学信息科学与工程学院教授，主要研究方向为数据处理与挖掘、逻辑电路设计、多维索引与查询优化。

董一鸿（1969-），男，博士，宁波大学信息科学与工程学院教授，主要研究方向为大数据、数据挖掘和人工智能。

陈华辉（1964-），男，博士，宁波大学信息科学与工程学院教授，主要研究方向为数据处理与挖掘、云计算。

2017-03-22；

：2017-06-07

国家自然科学基金资助项目（No.61472194，No.61572266）；浙江省自然科学基金资助项目（No.LY16F020003）

Foundations Items: The National Natural Science Foundation of China (No.61472194, No.61572266), Zhejiang Provincial Natural Science Foundation of China (No. LY16F020003)