红外纸张厚度测量中参数选取的模型研究

郇 帅，莫长涛

(哈尔滨商业大学 基础科学学院，哈尔滨 150028)

红外纸张厚度测量中参数选取的模型研究

郇 帅，莫长涛

(哈尔滨商业大学 基础科学学院，哈尔滨 150028)

在红外纸张厚度测量系统研究过程中，厚度用系统输出电压表征.在研究过程中，准确找出系统输出电压与待测样品厚度之间的对应关系是系统工作的精髓.然而，工作距离、供电电流与频率等参数会影响厚度检测的精度，合理选择最佳工作距离、最佳供电电流与最佳频率成为本系统研究的重要目的.通过前期大量实验，对数据进行分析整合，通过Matlab软件建立起数学模型，对该数学模型的求解与计算，确立其中的参数并确定最终数学表达式.将所建立模型和批量实验数据结合对比，发现通过模型找出的最佳工作距离、最佳供电电流与最佳频率和实验选取的最佳参数完全相同，得出模型建立正确的结论.为后续系统在工业中应用选择最佳参数提供坚实的理论与实验基础.

红外；理论推广；建模；光学传感

红外纸张水分及厚度测量的在线检测是一种非接触式的测量方法.它采用红外测量技术，将特定波长的多束红外光轮流照射到高速移动的纸张上，利用纸张的各种组份对红外的不同的吸收特性，对收集到的带有不同吸收信息的红外信号进行运算处理，得出水分和厚度两个测量值(即纸张水分，纸张定量)[1].在红外纸张水分及定量测量系统中，由于外界因素如光源频率、供电电流的不同往往影响纸张水分及定量的检测精度，为切入研究，先针对纸张厚度与输出电压之间的关系进行着手，为找到最佳工作距离与最佳供电电流等参数成为保证测量系统最佳工作状态的关键难点[2].

本研究通过先期大量物理实验、数学分析与数学建模克服上述难点，提出一种数学模型，通过Matlab软件进行数据拟合、作图分析直至模型建立，通过实验数据带入的计算与验证，发现通过建立模型找出的最佳工作距离与最佳供电电流和实验选取的最佳参数完全相同，得出模型建立正确的结论.通过该方法，可应用计算机语言写入检测系统硬件中，在应用时针对不同的环境选定最佳工作参数来提高检测精度，对后续系统的人性化开发具有重大意义.

随着控制理论和计算机技术的发展，制浆造纸工业的自动化也得到了较快发展.国外对制浆过程计算机控制的研究始于20世纪60年代末，在此期间，研究者建立了各种能适用于计算机控制的数学模型，20世纪70年代初出现了以电子计算机为中心的对整个制浆过程进行控制的自动化系统[3].目前，国外先进的间歇计算机控制系统一般都是由过程级、优化级和管理级三级组成，能对整个制浆过程的能源、原料、药液和产量进行优化、管理和控制.国外对回收过程的动态建模和控制方面建立的各种模型大多是过阻尼类的线性模型，很难解释多效蒸发系统的欠阻尼振荡现象，然而控制策略大多是采用PID反馈加前馈的传统控制方法，现代控制理论的应用还不成熟.在纸张厚度检测过程中对最佳发射-接收工作距离与最佳供电电流的参数选定模型研究尚未发现.本研究通过建立数学模型，拟合分析形成数学模型表达式，与大量实验数据比对后，发现实验数据是数学模型的解，实现了纸张厚度检测中最佳参数选取能力的提升，从而在理论上有了进一步的升华.

1 基本原理

1.1比尔-朗伯定律

假设有一平面光波在各向同性的均匀媒质中传播.经过厚度为的平行薄层后，光强从I变到IdI.朗伯(Lambert)指出：dI/I应与吸收层的厚度dl成正比，即

dI/I=-kdl

(1)

其中：k为吸收系数，由媒质的特性决定.对于厚度为l的介质层，由式(1)得

lnI=-kl+C

(2)

其中：c为一积分常数，如当l=0时，I=I0，则C=lnI0代入式(2)有

I=I0e-kl

(3)

这就是朗伯定律的数学表达式.

固体材料的吸收系数主要是随入射光波长而变，其他因素影响较小.而液体的吸收系数却与液体的浓度有关[4].实验证明，在很多情况下，当气体的分子或溶解在溶剂(实际上是不吸收光的溶剂)里的某些物质的分子吸收光时，吸收系数跟光波通过的路程上单位长度内吸收光的分子数也就是跟浓度c成正比.因此，比尔指出：溶液的吸收系数k与浓度c成正比.

k=α′c

此处α′为一个与浓度无关的新常数，它只决定于分子的特性，于是式(3)变为

I=I0e-α′cl

(4)

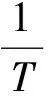
或A=αcl

(5)

式(5)即为朗伯-比尔定律的数学形式.在朗伯-比尔定律成立时，就可用测量吸收的方法来测定物质的厚度[5].这就是快速测定物质厚度的吸收光谱分析法.在实际中很有用处.

1.2模型建立

纸张水分通过比尔-朗伯定律中的浓度c确定；在已知纸张面积的前提下纸张定量与纸张厚度有关，通过比尔-朗伯定律中的l确定.在控制变量法的应用下，输出电压U(即光强I)与c和l都可单独确立一一对应的检测关系.为简化研究对象，本研究先以检测纸张定量为例进行建模，通过控制变量法分析当光源频率不变时选定最佳；当最佳不变时选定最佳光源频率，从而确立在光源频率与为最佳时，输出电压U与厚度l的一一对应检测关系.为此，我们引入数学思想即：

1)厚度l与输出电压U之间呈e指数衰减关系.

U1=U10e-αcl

(6)

为统一公式参数形式，将式(6)变为

U1=k1·e-a1l

(7)

a1=α·c，即吸收系数与浓度的乘积，通过实验，a1=0.00135.

2)通过实验发现，频率f与输出电压U之间近似呈平方与e指数衰减叠加的关系，拟定方程

U2=k2·f2·e-a2f

(8)

3)在频率f不变、供电电流I与输出电压U呈线性关系

U3=k3·I

(9)

实验采用控制变量法，拟定最终输出电压U作为检测结果，可认为输出电压U是U1、U2、U3的乘积，来研究厚度l、频率f及工作电流对输出电压的影响效果，找到最佳参数.

U=U1·U2·U3

(10)

即

U=k1e-a1l·k2f2e-a2f·k3I

(11)

考虑利用控制变量法符合全微分，对式(10)两侧取全微分得

dU=d(U1·U2·U3)

(12)

dU=U2U3dU1+U1U3dU2+U1U2dU3

(13)

推导得

dU=d(k1e-a1l·k2f2e-a2f·k3I)

(14)

此式的物理意义为最终的输出电压U由三个参量厚度l、频率f及工作电流I共同决定.在厚度不变，电流不变时选择最佳频率；在厚度不变，频率不变时选择最佳电流；选择最佳频率及最佳电流后将参数确定为系统检测参数，从而可实现厚度与输出电压U的一一对应关系，此变化规律符合控制变量法，又符合全微分计算思想，应用后可满足纸张定量的需求.

2 实验结果

通过先期实验数据U、l、I、f之间，实验数据如表1所示.

表1实验拟合参数表(f=100Hz)

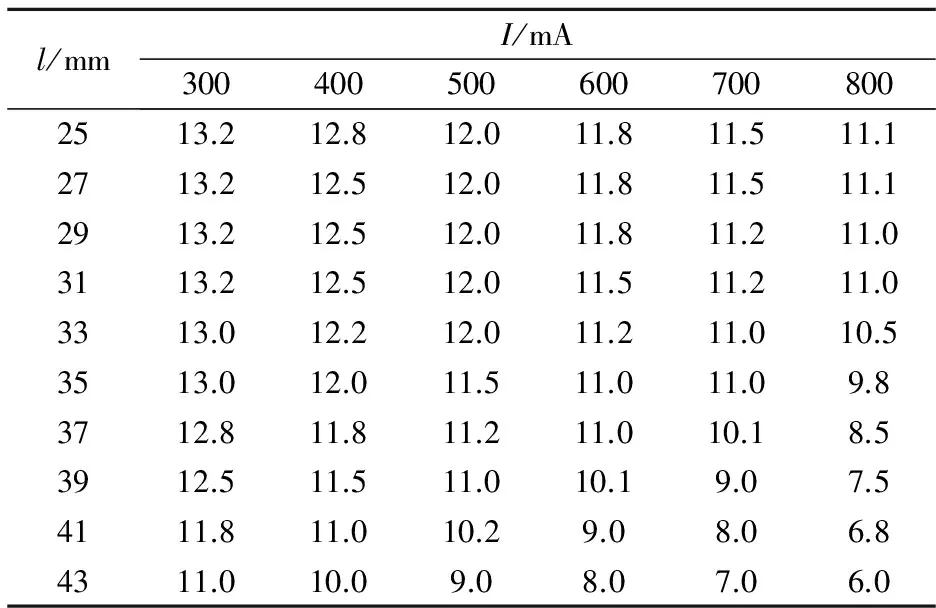
l/mmI/mA3004005006007008002513．212．812．011．811．511．12713．212．512．011．811．511．12913．212．512．011．811．211．03113．212．512．011．511．211．03313．012．212．011．211．010．53513．012．011．511．011．09．83712．811．811．211．010．18．53912．511．511．010．19．07．54111．811．010．29．08．06．84311．010．09．08．07．06．0

3 分析与讨论

利用数学软件对实验数据作图并分析研究后，对式(14)进行迭代计算，式中部分参数在先期实验中，由于所选取的材料确定，浓度确定，标准膜片的厚度确定，同时考虑实验仪器采用相对光强变化测量法.

通过计算得出(11)式的最终表达式为

U=13306.32e-0.00135l·f2e-0.00114f·I

(15)

可见厚度l、电流I及频率f共同对输出结果具有一定的影响，通过对模型式(15)与实验数据的对比分析表明，实验数据具有一定的拟合性，通过建立模型求解的最佳参数组，符合实验中通过数据筛选出的最佳条件，实现了模型建立的成功.

4 结 语

通过本模型的建立可以得出用厚度l、频率f及电流I乘积的方式作为整体输出电压U具有一定物理意义.按照实验设计思路，对几个变量乘积并且取全微分符合选取最佳参数的 创新思想，建立模型并对其中的系数进行最优化求解，确定模型数学表达式.若将此模型写入传感系统中并进行编译，可使纸张定量检测系统以及纸张水分检测系统实现最优化参数选取，为纸张水分及定量系统的研究奠定了一定的模型理论基础.为此，可扩展此思想应用于纸张水分及定量测量中，是提高系统精度与线性度的根本[6-7]，在传感器制作行业领域具有重大意义.

[1] 徐广通, 袁洪福, 陆婉珍. 现代近红外光谱技术及应用进展[J]. 光谱学与光谱分析, 2010, 20(2): 134-142.

[2] 莫长涛, 郇 帅, 苏海林. 近红外LED光源塑料薄膜的厚度测量[J].物理实验, 2016, 36(1): 9-13.

[3] 汤 伟, 施颂椒. 抄纸过程的建模、检测及控制[J]. 中国造纸, 2000, 11(6): 53-58.

[4] 郇 帅, 吕 加, 王 明, 等. 基于光谱吸收法经皮给药药液浓度检测研究[J]. 哈尔滨商业大学校报：自然科学版, 2014, 30(3): 332-334.

[5] 苏海林, 赵 娣. 低能γ射线反散射法测量塑料薄膜厚度的研究[J].传感器与检测技术, 2006, 27(6): 455-457.

[6] HU Z, MA Y B, HUAN S, ZHANG L. Design and Application of Fiber-Bragg-Grating Strain Tube[J]. ActaOpticaSinica,2011,31(S1).pp.s100314

[7] 胡志新, 马云宾, 郇 帅, 等. 光纤光栅应变管的设计与应用[J]. 光学学报, 2011, 31(S1): s100314.

Studyonparameterselectionofinfraredpaperthicknessmeasurement

HUAN Shuai, MO Chang-tao

(School of Basic Science, Harbin University of Commerce, Harbin 150028, China)

In the study of infrared paper thickness measurement system, the output voltage of the system is characterized by the thickness of the system. In the course of the study, it is the essence of the system to find out the corresponding relationship between the output voltage of the system and the thickness of the sample to be measured. However, working distance, power supply current and other parameters will affect the accuracy of the thickness measurement. The reasonable choice of the best working distance and the best supply current has become an important purpose of this system. Through a lot of experiments, the data were analyzed and integrated, the mathematical model was established by Matlab software, and the mathematical model was solved and calculated. The parameters were established, and the final mathematical expression was determined. The models and experimental data compared with the batch, found by the model to find out the best working distance optimal parameter selection and optimal power supply current and the same. The model set up a correct conclusion. Solid theoretical and experimental basis for the selection of the optimal parameters are used to the following systems in industry.

infrared; theory generalization; modeling; optical sensing

2016-10-10.

黑龙江省自然科学基金项目(A2015019)

郇 帅(1981-)，男，硕士，工程师，研究方向：物理电子学.

O657

：A

1672-0946(2017)04-0441-03