基于土壤入渗变异性的畦灌单宽流量优化

聂卫波，张 凡，马孝义，黄 恒（. 西安理工大学水资源研究所，西安 70048；. 西北农林科技大学旱区农业水土工程教育部重点实验室，杨凌 700）

基于土壤入渗变异性的畦灌单宽流量优化

聂卫波1，张 凡1，马孝义2，黄 恒1
（1. 西安理工大学水资源研究所，西安 710048；
2. 西北农林科技大学旱区农业水土工程教育部重点实验室，杨凌 712100）

农田土壤入渗变异性给畦灌系统的设计和管理带来了困难。为进一步提高畦灌灌水质量，该研究利用已有考虑土壤变异条件下的畦灌灌水质量计算模型，采用数值模拟与理论分析相结合的方法，扩展了模型的使用范围，并结合畦灌试验资料对其进行了验证；在此基础上分析了土壤入渗变异性对畦灌灌水质量的影响，提出了考虑农田土壤入渗变异条件下入畦单宽流量的确定方法。结果表明，文中扩展后的模型可用于计算异质土壤和均质土壤情景模式下的畦灌灌水质量指标，其计算值与田间实测值和WinSRFR软件模拟值一致性较好，相对误差均值分别为10%；土壤入渗变异对畦灌灌水质量的影响显著，贡献度高达56.71%～95.68%，其对灌水均匀度的影响最为敏感，其次为灌水效率和储水效率；基于均质土壤入渗条件下优化的入畦单宽流量，可用于异质土壤畦灌灌水流量设计，两者符合1∶1的线性关系。研究结果可为考虑农田土壤变异性的畦灌系统设计和管理提供理论依据和技术支撑。

土壤；入渗；模型；畦灌；变异性；数值模拟；灌水质量；入畦单宽流量

0 引 言

畦灌是密植作物广泛采用的灌水技术，但灌水质量不高仍是目前存在的主要问题。国内外学者针对该问题进行了大量研究，其中郑和祥等[1]建议通过优化田块规格来提高畦灌灌水质量；Sanchez等[2]、马娟娟等[3]和Koech等[4]分别以田间灌水试验的基础开展了相应的研究，其结果均表明通过选择合理的灌水流量和停水时间可获得较高的灌水质量；缴锡云等[5]采用田口方法对畦灌技术要素组合进行了设计，增强了设计结果的稳健性；吴彩丽等[6]采用数值模拟和理论分析相结合的方法，提出了不同灌溉技术要素组合下满足灌溉性能综合最优的灌水深度控制目标适宜值；白美健等[7]研究表明选用合理的关口时间（改水成数）能有效提高畦灌灌水质量；以上研究较好地促进了畦灌系统的设计和管理水平，但同时在其研究过程中较少考虑农田土壤入渗变异性对畦灌灌水质量影响，通常对入渗参数取均值进行简化处理，使其研究结果与田间实际情况有所差异，导致畦灌灌水质量的提高幅度有限。

近年来，部分学者开展了农田土壤入渗变异性对地面灌溉灌水质量影响的量化研究。根据Oyonarte等[8]的研究表明，沟灌过程中土壤入渗参数的变异性是影响灌水质量变化的主要因素，其贡献率在45%～75%之间；Mateos等[9]分析了土壤稳渗率对沟灌灌水质量的影响，结果表明考虑土壤稳渗率变异性的灌水均匀度低于未考虑其变异评价结果的20%以上；缴锡云等[10]研究表明考虑土壤入渗参数变异性的灌水效率相对于未考虑时降低了10%左右，灌水均匀度降低20%以上；白美健等[11]研究表明土壤入渗变异性对灌溉均匀度和灌溉效率影响较大，且变异越强畦灌质量越差；Nie等[12]以修正Kostiakov入渗公式为基础，建立了考虑土壤入渗变异影响的畦灌灌水质量评价模型；上述研究表明土壤入渗变异性对灌水质量的影响显著，在实际的应用中不容忽视，应在畦灌灌水质量评价和灌水方案设计时充分考虑其影响，但以往对于考虑农田土壤入渗变异条件下如何确定畦灌灌水技术要素的方法缺乏相应的研究。基于此，本文以文献[12]所建的考虑土壤入渗变异条件下的畦灌灌水质量评价模型为基础，通过扩展模型的使用范围，分析土壤入渗变异性对畦灌灌水质量的影响，提出考虑农田土壤入渗变异条件下入畦单宽流量的确定方法，以期进一步提高畦灌灌水质量，为畦灌系统设计和管理提供理论依据和技术支撑。

1 材料与方法

畦灌土壤水分分布主要取决于灌水过程中不同位置处入渗时间的差异和土壤入渗特性的变异特征，其不同位置处入渗时间的差异可根据水流消退和推进过程数据求得，而土壤入渗变异性可采用入渗公式中各参数的变异表征。考虑土壤入渗变异条件下的畦灌灌水质量评价模型分析与计算过程详见文献[12]，此处仅概括总结。

1.1 畦灌入渗时间变异性

畦灌水流推进和消退过程，分别采用幂函数和一元二次函数表征，即

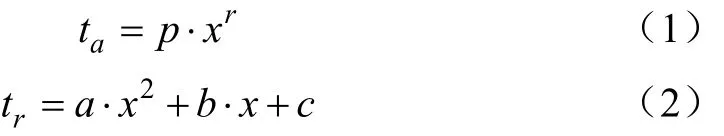
式中at和rt分别为水流推进和消退时间，min；x为水流至畦首距离，m；p、r、a、b和c均为经验系数，可利用水流运动过程资料采用多点回归拟合得到。根据研究可得畦灌过程中整个田面平均入渗时间和入渗时间方差[13]，即

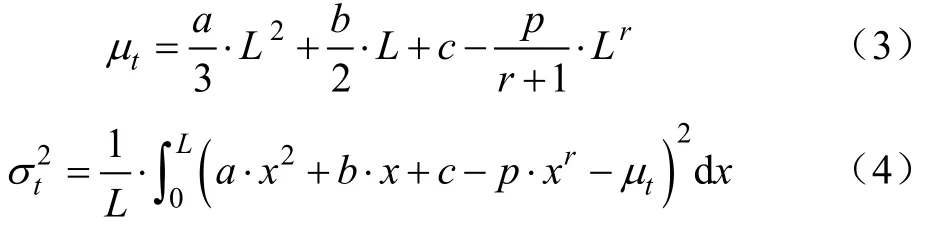
式中L为畦田长度，m；μt为田面平均入渗时间，min；为整个田面入渗时间方差，min2

1.2 畦灌土壤入渗变异性

采用修正Kostiakov公式[14]描述畦灌过程中的土壤入渗过程，即

式中Z为单位面积累积入渗量，mm；t为入渗时间，min；k为入渗系数，mm/minα；α为入渗指数；0f为稳渗率，mm/min；其参数可通过田间入渗试验或利用水流运动资料推求。关于土壤入渗变异性已取得了较多研究成果，其中白美健等[15]和聂卫波等[16]分别以双环入渗试验资料为基础，研究结果均表明式（5）中入渗指数α的变异性最小，它主要与土壤质地等因素有关，而农田尺度土壤质地相对均一，使得入渗指数α较为稳定，故可取均值，且与180Z（180 min的累积入渗量）无相关性；而入渗系数k和0f与180Z具有显著的相关性，可借助k和0f的变异性描述土壤入渗变异特征，但采用多变量（k和0f）给其分析带来了较大困难。因此，通过对式（5）进行归一化处理可简化该问题的研究，具体计算过程参见文献[17]，可得

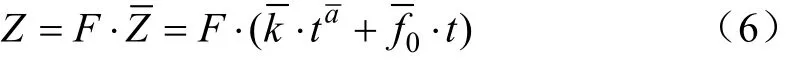
式中CV为畦田所有测点归一化因子F的变异系数。通过分析式（8）和式（9）可知，若CV=0，则可得均质土壤条件下，畦灌过程中整个田面累积入渗量的方差计算公式，即

1.3 畦灌灌水质量评价指标计算模型

畦灌灌水质量评价指标通常包括灌水效率Ea、储水效率Es和灌水均匀度Du，其中Du表征田间灌溉水在田面各点分布的均匀程度，可根据下式计算[12]，即

式中σZ为畦灌过程中整个田面累积入渗量的标准差，mm。根据Mateos等[9]研究成果，可得畦灌灌水效率Ea和储水效率Es指标计算公式，即

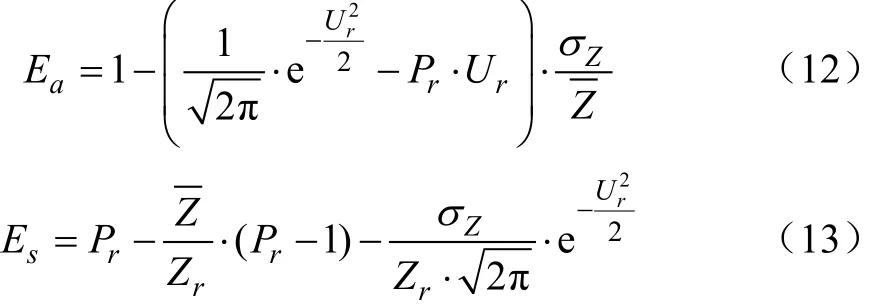
式中rU为标准正态分布条件下的计划灌水量，mm；rP为入渗水量大于rU时累计概率密度函数；rZ为计划灌水量，mm。rP和rU可分别根据下式计算

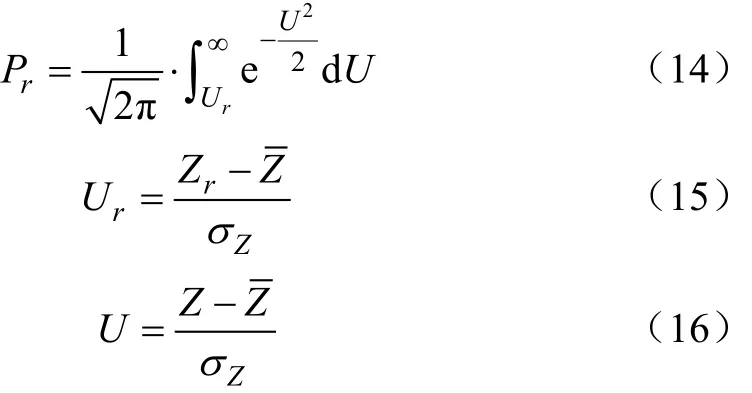
式中U为标准正态分布条件下的累积入渗量，mm。

1.4 畦灌模拟及单宽流量优化

WinSRFR软件是美国水保实验室开发的一维地面灌溉模拟模型，它是集地面灌溉评价、设计和模拟为一体的综合性分析软件[22-23]。大量学者研究表明WinSRFR软件能够很好地模拟地面灌溉水流运动过程和灌水质量指标[24-26]。因此，本文采用WinSRFR软件模拟畦灌过程，模拟分为2种情景模式，即情景1：均质土壤条件下畦灌过程模拟；情景2：考虑土壤变异条件下畦灌过程模拟。以软件模拟结果作为基准，验证文中方法估算灌水质量指标的可靠性。

由于畦灌灌水质量所采用的3个评价指标往往相互矛盾，且在评价指标制定时还需考虑存在极值的情况。因此，采用与文献[27]类似的方法，以灌水质量评价指标几何平均值最大作为准则，即

式中Y为畦灌灌水质量综合指标。以往通常选取可控的灌水流量和灌水时间来提高灌水质量，但在土壤入渗变异性的影响下，基于畦田均质土壤条件下优化的结果可能无法保证水流推进至田块尾部。因此，考虑田间实际情况和优化结果的实用性，本文在优化均质土壤和异质土壤2种情景模式下的灌水技术要素时，其灌水时间均采用水流推进至畦尾停水，主要通过选取合理的入畦单宽流量提高灌水质量。

1.5 畦灌试验

畦灌试验B1～B4于2016年1月在陕西省武功县进行，种植作物为冬小麦，该试验地点经、纬度分别为108°03′06′E，34°21′32′N。土壤质地为粉砂质壤土，平均干容重为1.51 g/cm3；试验前测定畦田坡降为3‰，入畦流量用三角薄壁堰测定求得，计划灌水量100 mm (B1～B4田块实际灌水量分别为125, 150, 115和119 mm)；畦田中每隔10 m设立观测点并记录水流推进和消退时间；灌水前、后1 d，沿畦长方向每隔10 m处采集土样测定土壤含水率，其中B1和B2畦田各设置9个土壤含水率取样点，B3和B4畦田各设置7个取样点，采集深度分别为0.1、0.2、0.3、0.4、0.6、0.8、1.0 m，收集土壤灌前和灌后不同位置和深度处的含水率数据，基于文献[28]的方法计算灌水质量评价指标（Ea、Es和Du），简称实测值。沿畦长方向每隔10 m处设置双环入渗试验点，土壤入渗参数根据实测入渗数据确定，结果见表1。已有文献[27,29]研究表明，田面糙率的变异性对地面灌溉水流运动过程和灌水质量影响较小。因此，在WinSRFR模拟过程中，田面糙率采用本文试验条件相类似冬小麦畦灌试验代表值0.100[26]。同时，采用文献[30]的畦灌试验资料B5～B9进行分析。田间畦灌试验在河北省吴桥县彭庄村进行，种植作物为棉花，试验区经、纬度分别为116°22′02′E，37°39′N。土壤质地为粉壤土，平均干容重为1.43 g/cm3，田面坡降为1.3‰，水源为地下水，计划灌水量60 mm。试验过程中观测水流推进和消退过程、入畦流量、田面水深等基础数据。畦田各项基本参数见表1。

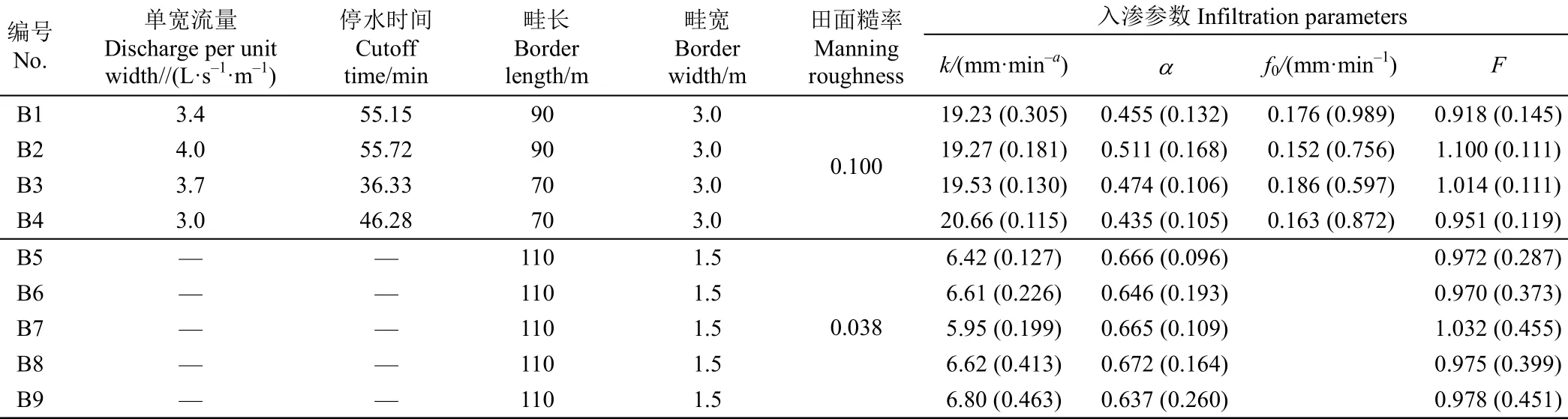
表1 不同畦田灌水试验基本参数Table 1 Basic parameters of border irrigation experiments for different border fields

2 结果与分析

2.1 畦田灌水质量评价模型验证

文献[12]已对表1中各畦田的土壤入渗特性进行了分析，并对归一化处理的修正Kastiakov入渗公式，即式（6）的可靠性进行了验证（归一化处理后累积入渗估算值与实测值决定系数R2=0.98，均方根误差为0.74 cm），在此不再赘述。以表1中的畦灌试验资料为基础，采用式（8）和式（10）分别计算异质土壤和均质土壤（CV=0）情景模式下田面累积入渗量的方差σZ21和σZ2

2，结合式（11）、式（12）和式（13）可得相应条件下畦灌灌水质量评价指标计算值，并与田间实测值进行对比，结果见表2。由表2可知，采用文中模型计算的土壤入渗变异条件下畦灌灌水质量指标与实测值具有高的一致性，其B1～B4畦田Du、Ea和Es的相对误差均值分别为5.40%、6.33%和5.53%，表明文中模型估算畦灌灌水质量指标具有高的精度，可较好地反映田间实际的灌溉水分布情况。而采用文中模型估算的均质土壤条件下，即CV=0的畦灌灌水质量指标与实测值具有较为显著的差异性，其中Du相对误差均值为15.42%，而Ea和Es的误差均值相对较小，分别为9.98%和5.66%，原因可能为：1）B1～B4畦田灌水量均大于计划灌水量（Zr=100 mm ），其中B2畦田灌水量最大为150 mm，B3最小为115 mm，即使土壤存在变异性，但过高的灌水量使得不同土壤条件下所计算的Ea和Es值基本一致，从而导致计算值与实测值相对误差较小；2）B1～B4畦田归一化因子F的变异系数CV值相对较小（表1），B1畦田的CV最大，但仅为0.145，其在一定程度上也使得均质土壤条件下，估算的畦田灌水质量指标aE和sE与实测值之间的差异较小。对比文中模型计算的异质土壤和均质土壤情景模式下灌水质量指标，结果表明畦灌过程中的土壤变异性对uD的影响最为敏感，对aE和sE的影响相对较小，两者基本一致，但需注意过高的灌水量可能降低了土壤变异性对aE和sE的影响。

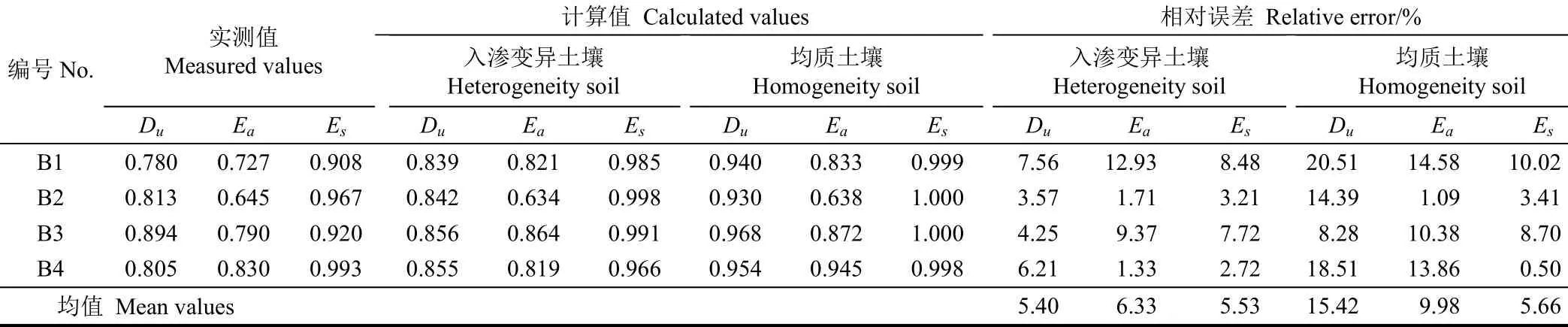
表2 畦田B1～B4灌水质量指标计算值与实测值对比Table 2 Calculated irrigation performance indicators compared with measured values of B1-B4 border fields

为进一步验证文中方法估算畦灌灌水质量指标的可靠性。采用式（11）、式（12）和式（13）分别计算表1中异质土壤和均质土壤（CV=0）情景模式下灌水质量指标，并与对应情景模式下WinSRFR软件模拟值进行对比，结果见图1。其中B1～B4畦田采用试验所用入畦流量和停水时间，B5～B9畦田由于文献[30]未给出具体数据，在模拟过程中入畦单宽流量分别采用3.0、5.0和7.0 L/(s·m)，水流推进至畦尾停水。由图1可见，畦灌灌水质量计算值与对应情景模式下WinSRFR软件模拟值具有较高的一致性，均分布在直线1∶1 两侧，其中异质土壤条件下，所有畦田灌水质量指标Du、Ea和Es的计算值与模拟值比较，两者相对误差（指各点相对误差绝对值的平均，下同）分别为7.08%、5.80%和4.49%；均质土壤条件下，所有畦田灌水质量指标Du、Ea和Es的计算值与模拟值相对误差分别为4.18%、8.12%和1.99%。由此可知，采用文中式（11）、式（12）和式（13）计算异质土壤和均质土壤情景模式下畦灌灌水质量指标均具有高的可靠性。

2.2 土壤变异性对畦灌灌水质量的影响

畦灌过程中土壤水分分布主要取决于整个田面累积入渗量的方差σZ2，通过计算不同变异项所占方差σZ2的比例，有助于理解土壤变异性对畦灌过程的影响，其中B5～B9畦田水流运动过程采用WinSRFR软件模拟，入畦单宽流量分别采用3.0、5.0和7.0 L/(s·m)，水流推进至畦尾停水，结果见表3。

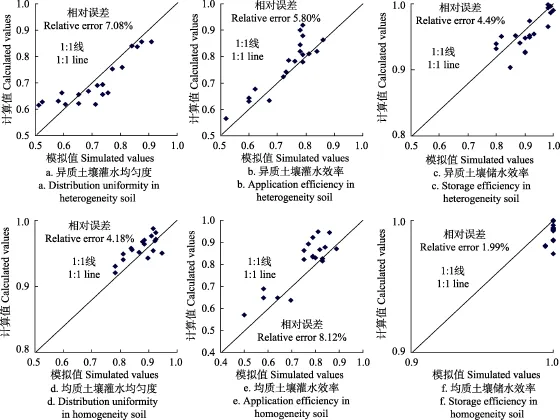
图1 异质土壤和均质土壤条件下畦灌灌水质量指标计算值与WinSRFR软件模拟值比较Fig. 1 Calculated irrigation performance values were compared with simulated values by WinSRFR under heterogeneity soil and homogeneity soil condition

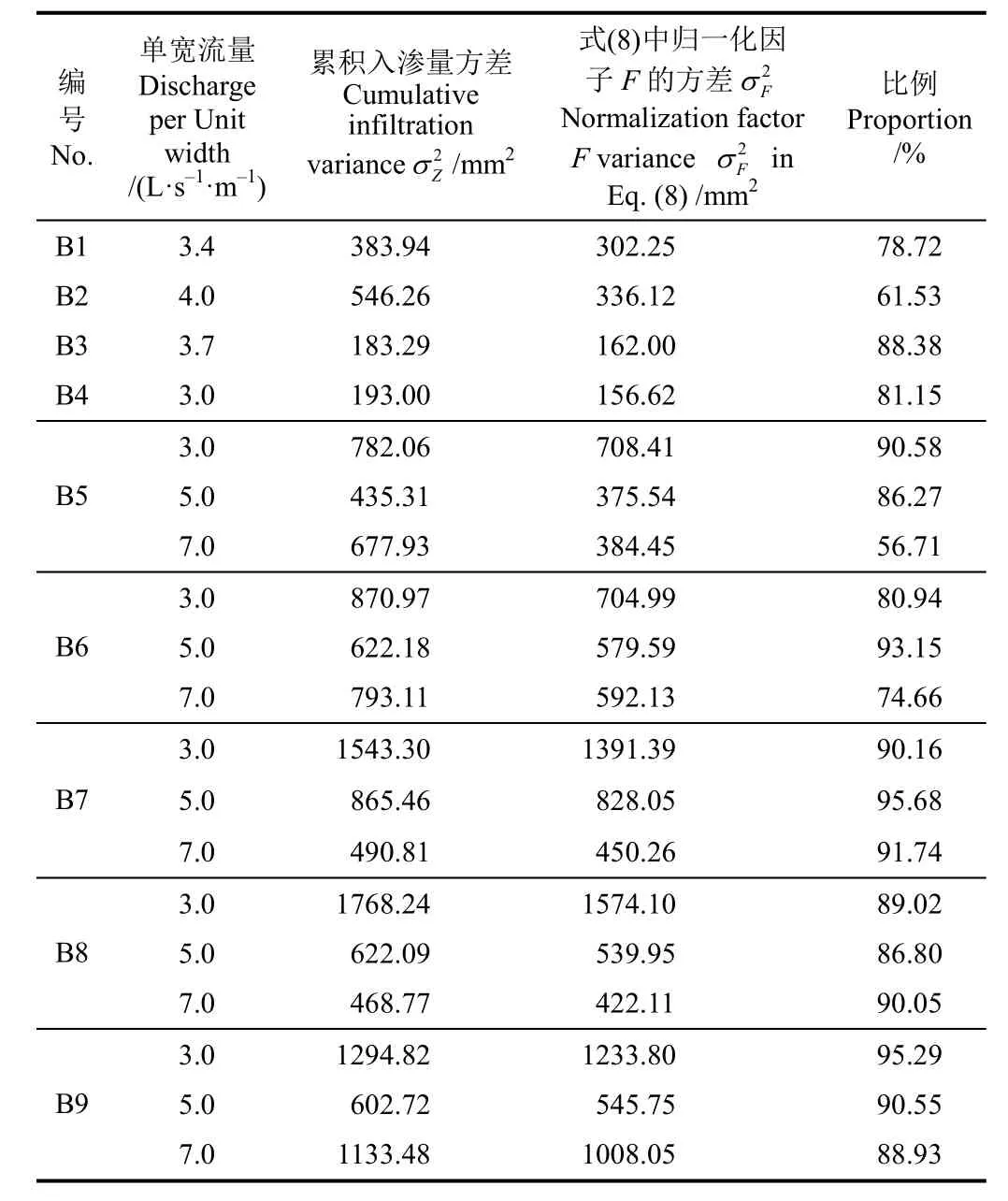
表3 畦灌土壤入渗变异占田面累积入渗量方差的比例Table 3 Proportion of soil infiltration variability in cumulative infiltration variance of border irrigation

由表3可知，土壤入渗变异项在整个田面累积入渗量的方差σZ2所占比例很高，其中最小为B5畦田在单宽流量为7.0 L/(s·m)时的56.71%，最大为B7畦田在单宽流量为5.0 L/(s·m)时的95.68%，这与Oyonarte等[8]对影响沟灌灌水质量变异源分析结果类似，但其土壤入渗变异所占比例范围（45%～71%）小于本文研究成果，原因为其分析过程中还考虑了湿周和湿周与灌水时间交互作用变异的影响，而对于畦灌过程而言，可不考虑上述因素影响，故使得土壤入渗变异项所占比例进一步增大。由此表明，在畦灌灌水质量评价过程中，需充分考虑土壤入渗变异性的影响，反之会使灌水质量指标计算值偏大，导致不能很好地反映田间实际。

通过对式（11）～式（13）分析可知，畦灌灌水质量指标与田面累积入渗量的方差有关，通过降低方差值，则可提高其灌水质量。而与土壤入渗变异项和田面入渗时间变异项密切相关，其中土壤入渗变异项所占方差比例很高，而土壤入渗变异是客观存在的，其入渗参数值和表征其变异的方差值较难改变，但可对田面平均入渗时间μt进行控制；对于田面入渗时间变异项，可通过降低μt和对其进行控制。通过分析式（3）和式（4）可知，畦灌中μt和值取决于畦长L和水流运动过程。考虑田间实际情况，畦长L通常采用田块实际长度；而水流运动过程是入畦流量、田面坡度、糙率和土壤入渗等特征的综合反映[31]，对于具体畦田而言，田面坡度和土壤入渗特性通常采用实际值，而灌水过程中田面糙率值与入畦流量和田面坡度等有关，故通过选取入畦流量作为控制变量，尽可能地降低畦灌中μt和值，从而减小土壤变异对畦灌灌水质量的影响。同时结合表3中B5～B9畦田可知，在其他条件不变的情况下，通过调整入畦单宽流量，结果表明田面累积入渗量的方差σ2有着显著的变化，这进一步支撑了可选取入畦流量

Z作为控制变量结论，为通过优化入畦单宽流量来提高畦灌灌水质量奠定了基础。

2.3 入畦单宽流量优化

对于均质土壤合理的入畦流量确定已有较多研究成果，若能建立异质土壤合理的入畦流量与均质土壤优化结果之间的关系，则可简化问题的研究。因此，采用式（11）～式（13）分别计算不同入畦单宽流量条件下异质土壤和均质土壤（CV=0）的灌水质量指标，并根据式（17）求出综合指标Y，其中水流运动过程采用WinSRFR软件模拟，入畦单宽流量分别采用2.0、3.0、4.0、5.0、6.0、7.0和8.0 L/(s·m)，水流推进至畦尾停水，结果见表4。由表4可知，无论是异质土壤还是均质土壤条件下，畦灌灌水质量综合指标Y均随入畦单宽流量的增大呈现出先增加后减小的趋势，符合抛物线型函数特征，其决定系数R2最小为0.727（P＜0.05），表明具有较高的拟合精度。对拟合所得函数进行求解，可分别求得异质土壤和均质土壤情景模式下各畦田最优的入畦单宽流量，结果见表5和图2。

表4 不同入畦单宽流量条件畦灌灌水质量综合指标Table 4 Comprehensive irrigation performance indicator of border irrigation under different discharge per unit width

由表5和图2可知，基于异质土壤条件下优化所得各田块入畦单宽流量与均质土壤条件下基本一致，两者差别较小，其均匀分布在1∶1线两则（R2=0.94，P＜0.05），表明基于均质土壤入渗条件下优化的入畦单宽流量结果，可用于异质土壤条件下畦灌灌水流量设计，能够保证高的灌水质量。通过分析式（8）和式（10）可知，由于土壤入渗变异是客观存在的，通过优化入畦单宽流量，可降低畦灌过程中μt和，即减小了田面累积入渗量的方差值，可使畦灌灌水质量达到最优。因此，从理论分析的角度而言，基于异质土壤和均质土壤条件下优化的入畦单宽流量应符合1∶1的线性关系，其为上述研究成果提供了理论基础。

根据表5中优化所得的入畦单宽流量，分别采用文中模型方法和WinSRFR软件对各畦田灌水质量指标进行计算，再根据式（17）求得综合指标Y，结果列于表5。由表5可知，无论是异质土壤还是均质土壤情景模式下，采用文中模型计算的Y值与WinSRFR软件模拟值基本一致，相对误差均小于10%，其中异质土壤条件下，所有畦田两者之间相对误差均值为2.48%，均质土壤条件下为1.67%，进一步表明采用文中模型计算异质土壤和均质土壤条件下的畦灌灌水质量指标是可靠的，具有高的计算精度。但同时发现部分畦田根据最优入畦流量计算的Y小于表4中的数值，原因为采用抛物线型函数存在一定的拟合误差。但总体而言，根据优化的入畦单宽流量，各畦田均可获得高的畦灌灌水质量。

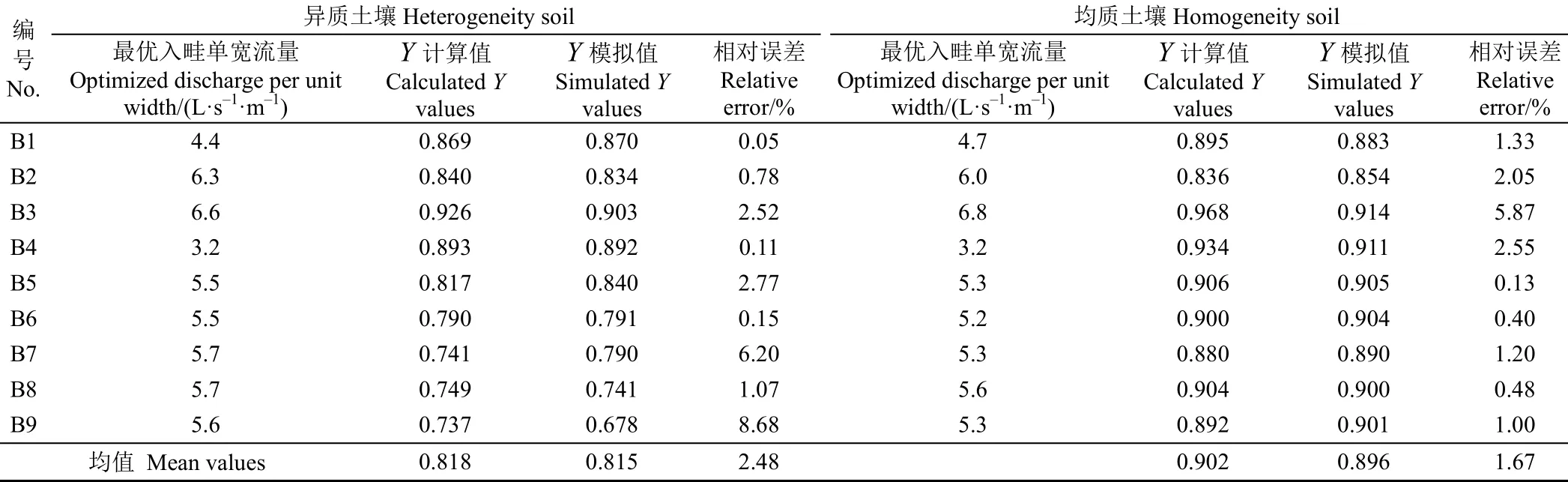
表5 异质土壤和均质土壤条件下入畦单宽流量优化结果及对应灌水质量综合指标Y值Table 5 Optimization results of discharge per unit width under heterogeneity and homogeneity soil and their corresponding comprehensive irrigation performance indicator Y values

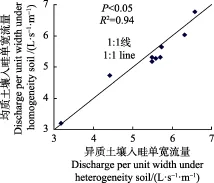
图2 均质与异质土壤入畦单宽流量优化结果比较Fig.2 Comparison of discharge per unit width optimization results in homogeneity and heterogeneity soil

3 结 论

本文采用数值模拟与理论分析相结合的方法，分析了土壤入渗变异对畦灌灌水质量的影响，得出如下结论：

1）扩展了考虑土壤入渗变异条件下畦灌灌水质量指标估算模型的适用范围。采用畦灌试验和数值模拟相结合的方法，对畦灌灌水质量估算模型进行了验证，结果表明无论是异质土壤还是均质土壤情景模式下，灌水质量指标计算值与田间实测值和WinSRFR软件模拟值均具有高的一致性，其相对误差均小于10%。

2）分析了土壤入渗变异和入渗时间变异对畦灌灌水质量的影响。结果表明土壤入渗变异对畦灌灌水质量的影响很大，所占比例为56.71%～95.68%，故在灌水质量评价过程中需充分考虑其影响；通过选取入畦流量作为优化变量，可降低入渗时间变异对畦灌灌水质量的影响，有助于提高畦灌灌水质量。

3）提出了考虑农田土壤变异下入畦单宽流量的确定方法。结果表明基于异质土壤和均质土壤条件下优化的入畦单宽流量符合1∶1的线性关系，即均质土壤入渗条件下优化的入畦单宽流量，可用于异质土壤条件下畦灌灌水流量设计。

本文研究过程中采用水流至畦尾停水的方式，未考虑改水成数、田面糙率和田面平整度等因素，其对文中结果可能有一定的影响，还需做进一步研究。

[1] 郑和祥，史海滨，程满金，等. 畦田灌水质量评价及水分利用效率分析[J]. 农业工程学报，2009，25(6)：1-6. Zheng Hexiang, Shi Haibin, Cheng Manjin, et al. Analysis of irrigation efficiency and water use efficiency of border irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(6): 1-6. (in Chinese with English abstract)

[2] Sanchez C A, Zerihun D, Farrell-Poe K L. Management guidelines for efficient irrigation of vegetables usingclosed-end level furrows[J]. Agricultural Water Management, 2009, 96(1): 43-52.

[3] 马娟娟，孙西欢，郭向红，等. 畦灌灌水技术参数的多目标模糊优化模型[J]. 排灌机械工程学报，2010，28(2)：160-163，178. Ma Juanjuan, Sun Xihua, Guo Xianghong, et al. Multi-objective fuzzy optimization model for border irrigation technical parameters[J]. Journal of Drainage and Irrigation Machinery Engineering, 2010, 28(2): 160-163, 178. (in Chinese with English abstract)

[4] Koech R K, Smith R J, Gillies M H. Evaluating the performance of a real-time optimisation system for furrow irrigation[J]. Agricultural Water Management, 2014, 142(1): 77-87.

[5] 缴锡云，王维汉，王志涛，等. 基于田口方法的畦灌稳健设计[J]. 水利学报，2013，44(3)：349-354. Jiao Xiyun, Wang Weihan, Wang Zhitao, et al. Robust design of border irrigation based on the taguchi method[J]. Journal of Hydraulic Engineering, 2013, 44(3): 349-354. (in Chinese with English abstract)

[6] 吴彩丽，徐迪，白美键，等. 不同灌水技术要素组合下畦灌灌水深度的控制目标[J]. 农业工程学报，2014，30(24)：67-73. Wu Caili, Xu Di, Bai Meijian, et al. Irrigation water depth control targets under different combination of irrigation technique elements for border irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(24): 67-73. (in Chinese with English abstract)

[7] 白美健，李益农，涂书芳，等. 畦灌关口时间优化改善灌水质量分析[J]. 农业工程学报，2016，32(2)：105-110. Bai Meijian, Li Yinong, Tu Shufang, et al. Analysis on cutoff time optimization of border irrigation to improve irrigated water quality[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(2): 105-110. (in Chinese with English abstract)

[8] Oyonarte N A, Mateos L, Palomo M J. Infiltration variability in furrow irrigation[J]. Journal of Irrigation and Drainage Engineering, 2002, 128(1): 26-33.

[9] Mateos L, Oyonarte N A. A spreadsheet model to evaluate sloping furrow irrigation accounting for infiltration variability[J]. Agricultural Water Management, 2005, 76(1): 62-75.

[10] 缴锡云，王维汉，王颖聪，等. 入渗参数空间变异规律及其对畦田灌水质量的影响[EB/OL].中国科技论文在线, 2009-12-28. http://www.paper.edu.cn/releasepaper/content/ 00912-1026. Jiao Xiyun, Wang Wenhan, Wang Yingcong, et al. Spatial variability of infiltration parameters and its impacts on irrigation performance[J/OL]. Sciencepaper Online, 2009-12-28. http://www.paper.edu.cn/releasepaper/content/ 00912-1026. (in Chinese with English abstract)

[11] 白美健，许迪，李益农. 不同微地形条件下入渗空间变异对畦灌性能影响分析[J]. 水利学报，2010，41(6)：732-738. Bai Meijian, Xu Di, Li Yinong. Effects of spatial variability of infiltration on basin irrigation performance under different microtopography conditions[J]. Journal of Hydraulic Engineering, 2010, 41(6): 732-738. (in Chinese with English abstract)

[12] Nie W B, Huang H, Ma X Y, et al. Evaluation of closed-end border irrigation accounting for soil infiltration variability[J]. Journal of Irrigation and Drainage Engineering, 2017, 143(6): 04017008. http://dx.doi.org/10.1061/(ASCE)IR.1943-4774. 0001174.

[13] 聂卫波，费良军，马孝义. 基于土壤入渗参数空间变异性的畦灌灌水质量评价[J]. 农业工程学报，2012，28(1)：100-105. Nie Weibo, Fei Liangjun, Ma Xiaoyi. Evaluation of border irrigation performance based on spatial variability of infiltration parameters[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(1): 100-105. (in Chinese with English abstract)

[14] Walker W R, Skogerboe G V. Surface Irrigation: Theory and Practice[M]. Englewood Cliffs, NJ: Prentice-Hall, 1987.

[15] 白美健，许迪，李益农，等. 地面灌溉土壤入渗参数时空变异性试验研究[J]. 水土保持学报，2005，19(5)：120-123，151. Bai Meijian, Xu Di, Li Yinong. Evaluating spatial and temporal variability of infiltration on field scale under surface irrigation[J]. Journal of Soil and Water Conservation, 2005, 19(5): 120-123, 151. (in Chinese with English abstract)

[16] 聂卫波，武世亮，马孝义，等. 农田土壤入渗特性的研究[J]. 干旱地区农业研究，2013，31(4)：31-37. Nie Weibo, Wu Shiliang, Ma Xiaoyi, et al. Research on the soil infiltration characteristics in the field[J]. Agricultural Research in the Arid Areas, 2013, 31(4): 31-37. (in Chinese with English abstract)

[17] 聂卫波，武世亮，马孝义，等. 田块尺度土壤入渗特性空间变异研究[J]. 农业工程学报，2014，30(9)：76-83. Nie Weibo, Wu Shiliang, Ma Xiaoyi, et al. Research on field-scale spatial variability of soil infiltration characteristics[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(9): 76-83. (inChinese with English abstract)

[18] Sharma M L, Gander G. A, Hunt C G. Spatially variability of infiltration in a watershed[J]. Journal of Hydrology, 1980, 45(1/2): 101-122.

[19] Gillies M H, Smith R J, Raine S R. Evaluating whole field irrigation performance using statistical inference of inter-furrow infiltration variation[J]. Biosystems Engineering, 2011, 110(2): 134-143.

[20] Jaynes D B, Clemmens A J. Accounting for spatially variable infiltration in border irrigation models[J]. Water Resources Research, 1986, 22(8): 1257-1262.

[21] Trout T J. Furrow inflow and infiltration variability impacts on irrigation management[J]. Transactions of the American Society of Agricultural Engineers, 1990, 33(4): 1171-1178

[22] Bautista E, Clemmens A J, Strelkoff T S, et al. Modern analysis of surface irrigation systems with WinSRFR[J]. Agricultural Water Management, 2009, 96(7): 1146-1154.

[23] Bautista E, Clemmens A J, Strelkoff T S, et al. Analysis of surface irrigation systems with WinSRFR-Example application[J]. Agricultural Water Management, 2009, 96(7):1162-1169.

[24] Gonzaleza C, Cerveraa L, Moret-Fernandez D. Basin irrigation design with longitudinal slope[J]. Agricultural Water Management, 2011, 98(10): 1516-1522.

[25] 蔡焕杰，徐家屯，王健，等. 基于WinSRFR模拟灌溉农田土壤入渗参数年变化规律[J]. 农业工程学报，2016，32(2)：92-98. Cai Huanjie, Xu Jiatun, Wang Jian, et al. Yearly variation of soil infiltration parameters in irrigated field based on WinSRFR4.1[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(2): 92-98. (in Chinese with English abstract)

[26] Bautista E. Effect of infiltration modeling approach on operational solutions for furrow irrigation[J]. Journal of Irrigation and Drainage Engineering, 2017, 143(6): 06016012. http://dx.doi.org/10.1061/(ASCE)IR.1943-4774. 0001090.

[27] 王维汉，缴锡云，彭世彰，等. 基于稳健设计理论的畦灌质量敏感性分析[J]. 农业工程学报，2010，26(11)：37-42. Wang Weihan, Jiao Xiyun, Peng Shizhang, et al. Sensitivity analysis of border irrigation performance using robust design theory[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(11): 37-42. (in Chinese with English abstract)

[28] 汪志农. 灌溉排水工程学：第1版[M]. 北京：中国农业出版社，2000.

[29] Nie WeiBo, Fei Liangjun, Ma Xiaoyi. Impact of infiltration parameters and Manning roughness on the advance trajectory and irrigation performance for closed-end furrows[J]. Spanish Journal of Agricultural Research, 2014, 12(4): 1180-1191.

[30] 缴锡云，王维汉. 沟畦灌溉稳健设计[M]. 南京：河海大学出版社，2012.

[31] 王全九，王文焰，张江辉，等. 根据畦田水流推进过程水力因素确定Philip入渗参数和田面平均糙率[J]. 水利学报, 2005，36(1)：125-128. Wnag Quanjiu, Wang Wenyan, Zhang Jianghui, et al. Determination of Philip infiltration parameter and Manning roughness according to hydraulic factors in the advance of irrigation water[J]. Journal of Hydraulic Engineering, 2005, 36(1): 125-128. (in Chinese with English abstract)

Optimization of discharge per unit width of border irrigation based on soil infiltration variability

Nie Weibo1, Zhang Fan1, Ma Xiaoyi2, Huang Heng1
(1. Institute of Water Resources, Xi’an University of Technology, Xi’an 710048, China; 2. Key Laboratory for Agricultural Soil and Water Engineering in Arid Area of Ministry of Education, Northwest Agriculture and Forestry University, Yangling, 712100, China)

Field soil infiltration variability has brought difficulties to the design and management of border irrigation system. In the previous researches, the effect of spatial variability of soil infiltration on water movement process and irrigation performance was not taken into consideration, which cannot reflect the actual situation in the field, resulting in the limitation of the improvement of border irrigation performance. In order to solve the above problems, based on the available calculation model of irrigation performance indicators of border irrigation under heterogeneity soil conditions, this study extended the range of the model application, and numerical simulation of border irrigation process were conducted by the WinSRFR software. Additionally, the calculation model was verified combined with the experimental data of border irrigation in Wugong county (108°03′06′E, 34°21′32′N) of Shaanxi Province and Pengzhuang village (116°22′02′E, 37°39′N) in Wuqiao county, Hebei Province. Based on the above researches, the calculation model of this study and theoretical analysis were adopted to analyze the influence of heterogeneity soil on the performance of border irrigation. Moreover, taking the maximum geometric average value of the distribution uniformity, application efficiency and storage efficiency as the optimization function, a method to determine the discharge per unit width under the consideration of soil infiltration variability was proposed. The results showed that through the expanded calculation model of border irrigation performance indicators under soil infiltration variation conditions, the proposed model was suitable not only for calculation the performance of border irrigation under the conditions of soil heterogeneity, but also for the calculation under the condition of homogeneous soil. Under the condition of soil heterogeneity, the calculated values of distribution uniformity, application efficiency and storage efficiency were in good agreement with the measured and simulation values by WinSRFR software, and the relative error was less than 8%. However, under the homogeneity soil condition, the error was relative large between the calculated and the measured values of irrigation performance indicators, of which the relative error of distribution uniformity had the largest value of 15.42%. The results indicated that the influence of soil infiltration variability should be taken into account in the process of irrigation performance evaluation. Otherwise, the results would be deviated from the actual situation in the field. While under the condition of homogeneous soil, the calculated values of irrigation performance and WinSRFR software had high consistency, and the relative error was less than 10%. Soil infiltration variation had a great influence on the performance of border irrigation, accounting for 56.71%-95.68%, and the influence should be taken into account in the process of irrigation performance evaluation. By selecting the discharge per unit width as an optimization variable, the effect of infiltration spatial variation on the performance of border irrigation could be reduced, which contributed to improvement of the border irrigation performance. The optimized discharge per unit width of the heterogeneity soil and homogeneity soil meets the 1:1 liner relationship, that is, the optimal discharge per unit width of the homogeneous soil could be used to the design of the discharge water of border irrigation under heterogeneity soil conditions, which guaranteed a high irrigation performance. The method proposed in this study can better reflect the actual performance of border irrigation, and provide theoretical and technical support for the design and management of border irrigation system.

soils; infiltration; models; border irrigation; variability; numerical simulation; irrigation performance; discharge per unit width

10.11975/j.issn.1002-6819.2017.16.016

S 275.3

A

1002-6819(2017)-16-0119-08

聂卫波，张 凡，马孝义，黄 恒. 基于土壤入渗变异性的畦灌单宽流量优化[J]. 农业工程学报，2017，33(16)：119 -126.

10.11975/j.issn.1002-6819.2017.16.016 http://www.tcsae.org

Nie Weibo, Zhang Fan, Ma Xiaoyi, Huang Heng. Optimization of discharge per unit width of border irrigation based on soil infiltration variability[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(16): 119-126. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.16.016 http://www.tcsae.org

2017-02-06

2017-07-10

国家自然科学基金项目（51579205、51209171）；国家重点研发计划项目（2016YFC0400203）；陕西省自然科学基金项目（2016JM5053）；陕西省教育厅重点实验室基金（15JS064）

聂卫波，男，陕西周至人，副教授，博士，主要从事农业水土工程方面研究。西安 西安理工大学水资源研究所，710048。

Email：nwbo2000@163.com.