魂芯DSP上复数类型的支持和优化①

王玉林, 郑启龙, 赵高义

1(中国科学技术大学 计算机科学与技术学院,合肥 230027)2(中国科学技术大学 安徽省高性能计算重点实验室,合肥 230027)

魂芯DSP上复数类型的支持和优化①

王玉林, 郑启龙, 赵高义

1(中国科学技术大学 计算机科学与技术学院,合肥 230027)2(中国科学技术大学 安徽省高性能计算重点实验室,合肥 230027)

魂芯DSP是一款采用VLIW和SIMD架构的针对高性能计算领域而设计的32bit静态标量数字信号处理器.为了满足数字高性能计算的性能要求,魂芯DSP提供了丰富的复数指令,而编译器不能直接利用这些复数指令来提升编译性能.因此针对魂芯DSP芯片提供了大量的复数类操作指令的特点,在传统开源编译器Open64的编译框架基础上进行研究,实现了复数作为编译器基础类型和复数运算操作的支持.同时,通过识别特定的复数类操作的模式利用魂芯DSP上的复数类指令对程序编译优化.实验结果表明,该实现方案在魂芯DSP编译器上对复数程序优化后能够取得平均5.28的加速比.

编译优化;分簇体系DSP;复数指令;Open64编译器

复数分为实部和虚部,可以用n=a+bi来表示一个复数:其中a表示复数的实部,b表示复数的实部.一次复数乘法操作n1×n2=(a+bi)×(c+di),要做4次乘法运算、1次加法运算、1次减法运算,在汇编语言层次,要6条指令来完成一次复数乘法的操作.

魂芯DSP[1]是中国电子科技集团第38研究所设计开发的一款高性能DSP,适用于雷达信号处理、电子对抗、通信保障等领域.魂芯DSP芯片提供了大量的复数运算类指令,但是现有的编译器框架是现有编译器框架无法识别出复数操作生成复数类指令,是通过把复数操作分解为实部和虚部单独处理来合成复数类的操作.复数加法或者减法至少需要2条指令,复数乘法就需要至少6条指令,无法利用魂芯DSP上单周期复数指令来对提升程序的性能.

本文重点介绍基于开源Open64编译器来完成对复数的支持和优化.主要是基于对开源编译器Open64的前端和后端的修改来完成复数类型的支持,利用魂芯DSP上特有的复数类指令来,通过定义一些复数类操作的模式,把本来需要几条指令才能完成的操作,优化成魂芯DSP上对应的一条指令.这种针对特定高效指令模式识别的方式也适用于其他的平台.

1 研究背景

当应用程序中存在大量的复数乘法操作时,程序执行时间相当程度上依赖于完成复数乘法操作的时间,快速傅里叶变换[2](Fast FourierTransform,FFT)程序中就存在很多循环的复数加法和乘法操作.

C语言的C99语法中规定了对复数操作的语法定义,对于复数的定义如下:

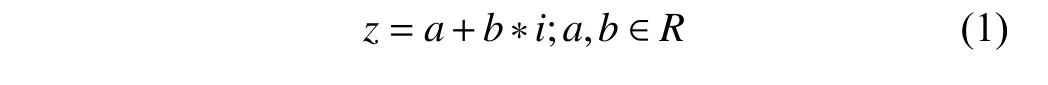
那么复数的乘法和除法定义为如下的操作,可以看出来复数操作要实数4次乘法、一此加法、一次减法,复数除法操作需要实数6次乘法、三次加法、两次除法、一次减法.

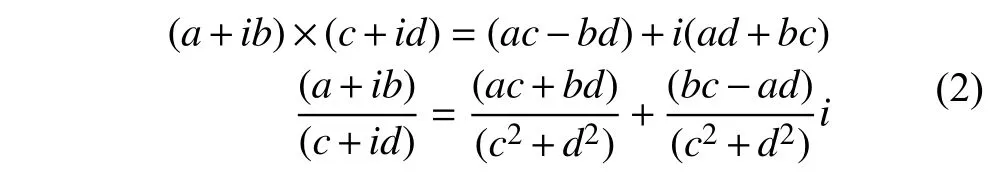
GCC编译器[3]前端从4.2版本以后就支持C99语法,也就是支持在C源程序支持复数的语义.但是GCC后端对复数操作的指令实现,是通过一组指令组合操作来得到复数操作的结果,没有对应的高效的复数指令.

BWDSP编译器采用开源Open64[4]编译器基础设施作为编译器研究框架,而Open64编译器是用的GCC的前端,所以原有的编译器框架在移植到魂芯DSP上后对复数操作的编译结果和原有的GCC中实现基本是一样的.Open64是一款GPL协议的工业级开源编译基础设施,以中后端提供的强大的分析优化能力著称.主要架构如图1所示.

Open64开源编译器前端采取的是GCC4.2前端,中间语言为抽象语法树ASTtree.高级语言经过前端时,以语法tree的形式存在,经由gspin(一种从gcc的tree到WHIRL转换的中间表示)的媒介,转换成为对应的WHIRL[5]中间语言.Open64的前端将源程序转化为中间表示WHIRL,后端读入WHIRL,经过翻译生成代码生成阶段(Code Generation,CG)的中间表示CGIR,在经过一系列优化,最终CGIR经过代码输出生成汇编程序.

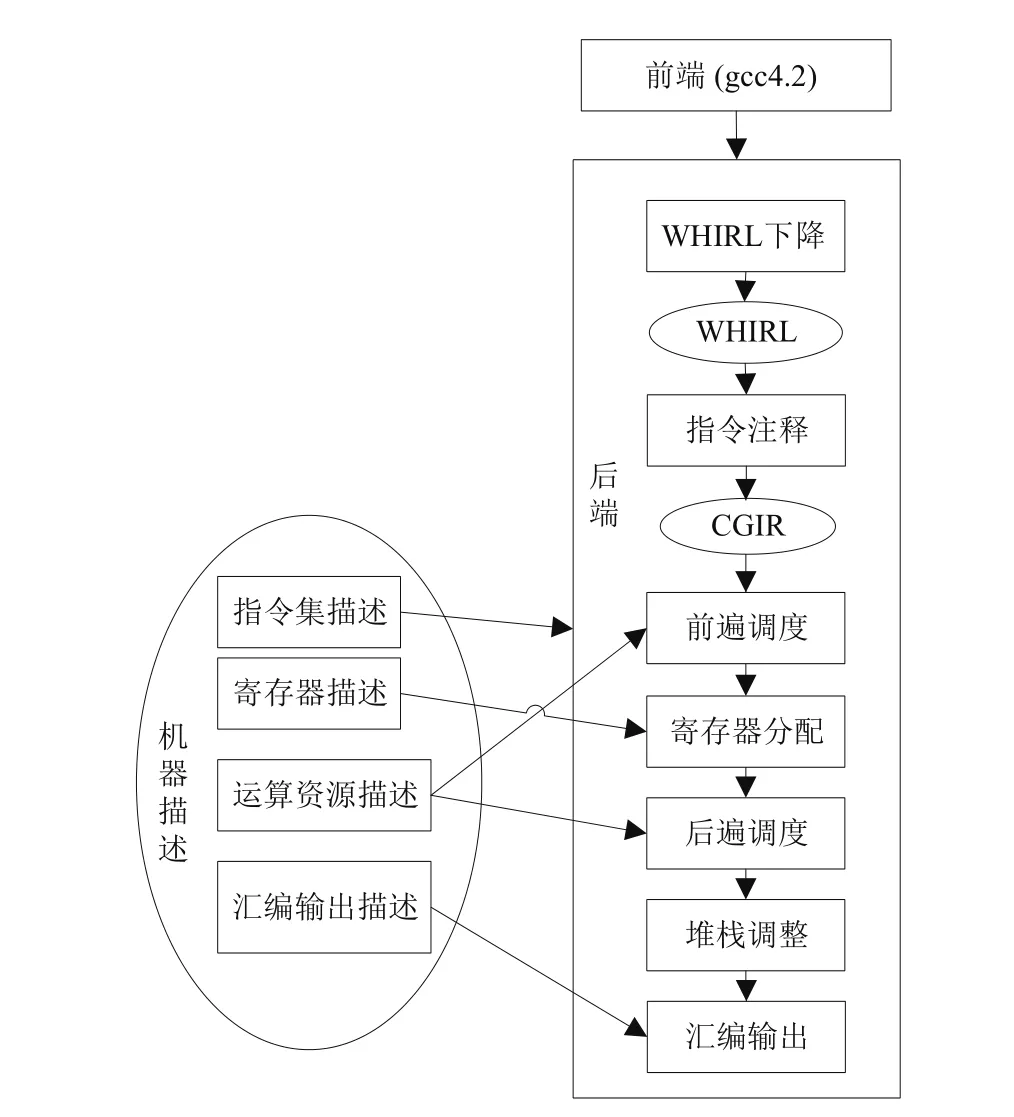
图1 Open64编译器架构

2 问题与解决方案

复数类型支持的基本的思路是把复数作为一种新的基础数据模型,为这个新的数据类型建立一套ADT(abstract data type)并利用Open64编译器框架实现和复数有关的数据操作,而不是把复数作为复合数据类型来处理.但是后前Open64编译器框架中并不把复数操作作为基础的数据类型,通过修改编译器的前端来禁止编译器把复数操作展开为实部和虚部.通过修改编译器后端的机器描述,以及在编译器WHIRL下降阶段通过识别出复数操作来处理针对复数运算的逻辑,利用魂芯DSP单周期复数指令,生成高效的汇编程序.

通过研究认为复数数据作为基础类型,具有如表1所示的原子操作定义.

复数类型作为编译器中的基础类型,表1中列出的操作在编译器中需要识别并实现为单条操作.对于编译器预期的结果则是汇编代码中除了复数其他操作对应于一条单周期的指令就可以完成对应的语义.

表1 复数数据类型的ADT

2.1 复数类型的支持

在魂芯DSP处理器提供了丰富的单周期复数指令.包括复数加减法、复数乘法、共轭复数运算[6]等.其中Macro表示该指令的分簇情况,由指令可以看出可以仅仅利用一条指令来解决一种复数运算操作.然而通常编译器对于复数的运算都会转化到实数范围内对复数的实部和虚部分别进行多次的实数运算之后再将实部和虚部分别写回,这样的处理方法使得程序并不能利用到DSP自身提供的各种复数运算指令.

{Macro}CFRs+1:s = CFRm+1:m + CFRn+1:n

{Macro}CFRs+1:s = CFRm+1:m - CFRn+1:n

{Macro}CFRs+1:s = CFRm+1:m * CFRn+1:n

{Macro}CFRs+1:s = conj CFRn+1:n

研究发现Open64开源编译器在编译优化的后期为了通用性考虑,把复数操作展开为实部和虚部的单独运算操作[7].所以重点工作在编译器框架的中端和后端部分.

Open64中经过前端词法和语法的分析会生成中间语法树WHIRL.WHIRL树中定义了一些列的操作算子opcode[8],其中每一个opcode就代表了程序的一个算子,可以通过识别复数操作的算子在WHIRL下降到CGIR的过程中增加针对魂芯DSP目标体系结构的处理逻辑,通过指令注释生成对应的汇编代码.

对于复数类型操作支持的解决方案流程如图2所示.主要分为三步:(1)前端禁止编译器把复数展开为实部和虚部;(2)修改编译器中端WHIRL节点定义增加复数操作的opcode码;(3)在编译器机器描述文件中增加复数操作的指令描述,修改编译器后端CGIR框架,增加对应WHIRL树种新增的复数的opcode的处理逻辑.

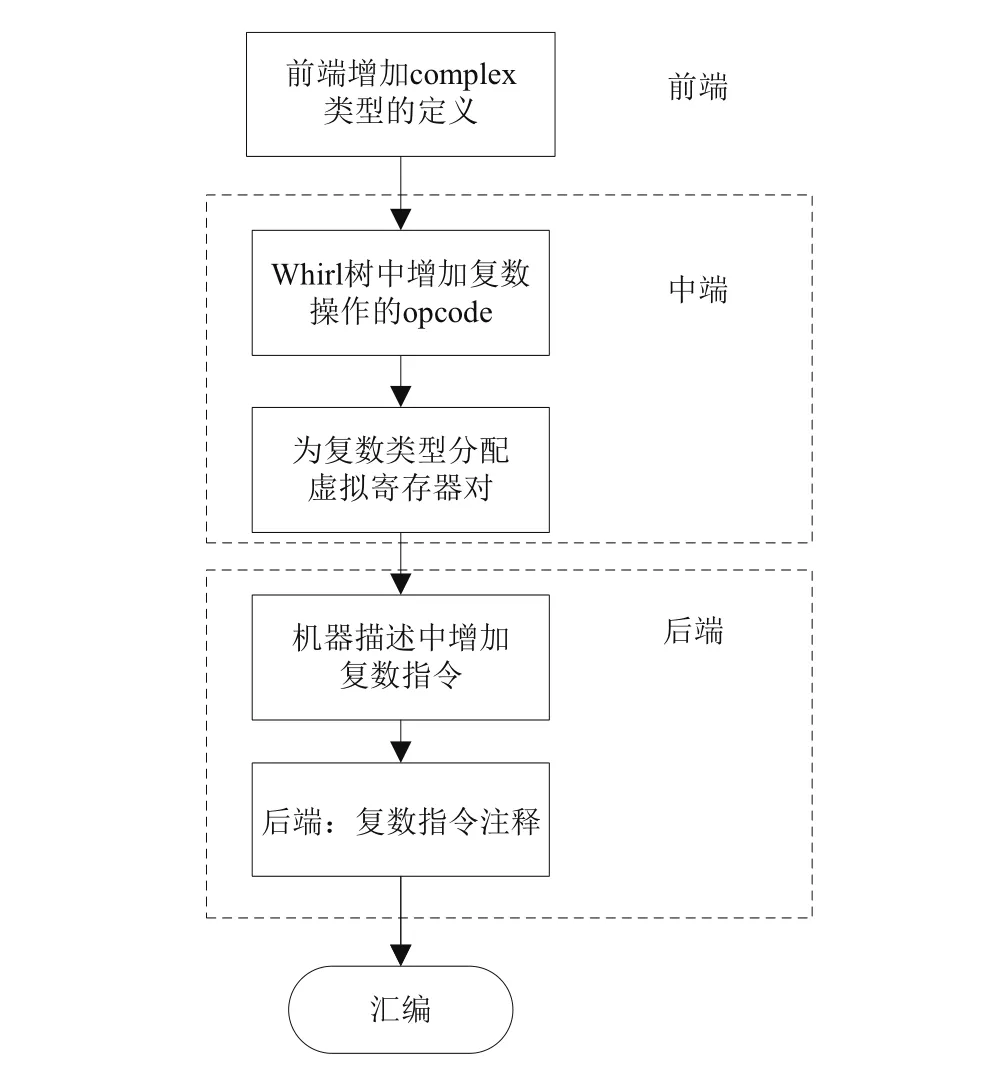
图2 复数类型支持流程

2.2 复数类型优化

魂芯DSP芯片除了提供复数基本的加减乘单周期指令外还提供了许多和复数操作相关的高效指令.指令形式如下:

{Macro}CFRs+1:s = CFRm+1:m + jCFRn+1:n

{Macro}CFRs+1:s = (CFRm+1:m + CFRn+1:n)/2

{Macro}CFRs+1:s = (CFRm+1:m + jCFRn+1:n)/2

{Macro}CFACCs+1:s += CFRn+1:n (conc,con=Rm)

第一个指令是一个复数同另一个复数乘上j后的浮点加法(等价于一个复数先乘上一个实数,然后运算的结果会存储为一个中间结果,然后中间结果再加上另外一个复数得到最后结果),第二条和第三条指令分别是复数相加除2指令和第一条指令运算结果再除2指令.最后一条指令是复数累加指令,累加的结果存在累加寄存器ACC中.因为编译器到后端一般是三地址代码,这些指令在Open64的中间WHIRL树中对应的并不是一条单一的opcode操作码,无法通过简单的代码翻译就可以利用到对应的高效指令,要通过合并几条特有的操作算子来翻译到魂芯DSP上高效的指令.

WHILR中节点是树的结构组织的,那么可以从树的根节点,也就是一个程序的region入口处开始遍历树的节点,当发现某一个子节点中的孩子节点有符合我们要优化的模式时就去匹配定义好的模式处理逻辑,把本来要好几条处理指令才能完成的逻辑用魂芯DSP上一条指令就可以完成,提高程序的指令效率.所以需要定义我们的遍历树节点的算法,对应的模式串和匹配到模式串后处理的算法.对WHIRL树节点的编译算法如图3所示.

图3 复数高效指令优化流程

算法首先判断WHIRL树节点中是否含有和复数操作有关的节点,如果包含复数操作的节点,那么就按已经确定好的优化模式串来对树的节点进行遍历,如果Match_Rule返回结果是真,那么就说明此树种有节点符合我们优化的模式.然后针对此节点进行优化处理,处理的逻辑在Do_Opt_Redule,这个子函数是用来对WHIRL中它包含的符合优化处理的一系列指令到CGIR的下降处理剪切我们预先定义的模式处理流程,然后在经过指令注释生成DSP上的高效的指令.

对于一个节点如何满足某个模式优化串,也就是Mach_Rule的流程,我们定义如下的模式串流程,如果WHIRL树种节点符合这种规则,则优化逻辑就对次节点进行优化,以上面列出的高效指令的第一个指令为例,其中模式串的规则定义如图4所示.首先判断tree节点中是否为复数加法操作,如果是然后在判断是否第二个操作数的孩子节点类型是否是复数和浮点数类型,如果条件都满足,那么就说明符合预定义的优化规则.

但是这种优化算法会带来编译器的编译速度的降低,对于DSP嵌入式设备来说,代码效率和代码大小是很重要的考量,这种优化逻辑既可以减少程序的执行周期又可以减少DSP上代码的大小.

图4 复数加乘优化Rule规则

3 实现中的核心问题

3.1 WHITL中增加复数操作码

Open64在从WHIRL树转换到CGIR的过程会进行一系列的优化,VHO,IPA,LNO,WOPT,CG[9].在最后一个优化阶段CG中增加对魂芯DSP目标平台的宏定义,禁止编译器框架把复数展开为复合操作,令WHIRL转换到CGIR模块则可以识别出复数为基础数据类型.

通过在编译器后端增加复数类型运算的操作码(opcode),来支持复数操作,在操作码文件opcode.h中增加复数运算操作码.例如增加复数加操作,OPC_C4ADD操作码表示是一条加法操作,输入的源操作的类型是32位的复数类型.通过增加转换条件来支持转换WHIRL转化为CGIR的中间表示,转化后的CGIR中的每条指令与魂芯DSP目标处理器指令集中的汇编指令格式一一对应.

MTYPE_C4=17 /* for 32-bit complex */

OPC_C4ADD=OPR_ADD+RTYPE(MTYPE_C4)+DESC(MTYPE_V)

在WHIRL转换到CGIR过程中通过识别出OPR_ADD操作,继而再判断操作数是复数类型,转到复数操作数的处理流程.

3.2 复数寄存器对分配

由于复数类型包含实部和虚部,所以对复数类型要分配两个连续编号的寄存器,即寄存器对.实部存放奇序号寄存器,虚部存放偶序号寄存器.对于连续编号寄存器对[10]的保证可以通过TN_Pair在寄存器分配中申请,TN_Pair表示两个连续编号的寄存器对,且较小编号为偶数.

TN_Pair的实现需要修改原有的框架中寄存器分配的算法.魂芯DSP编译器使用启发式的图着色算法进行全局的寄存器分配.基本的算法流程是先为函数中的寄存器建立寄存器干涉图[11],然后统计虚拟寄存器的使用频率,依照使用频率的大小依次进行着色.针对复数操作对寄存器的特殊要求,对寄存器分配算法修改.将复数指令上的所有寄存器看成是一个整体分配相应的连续寄存器.具体的实现是在寄存器分派阶段,为复数指令操作数分配寄存器时,将寄存器属性标记为R_CONTAINS_COMPLEX,并将这些寄存器添加到vreg_complex_list中,表示寄存器对为复数操作所需的寄存器.

3.3 复数类指令注释

在利用目标机器提供了有关复数运算的指令时,首先要对相关的目标或机器指令进行描述,以便在后端的分簇、指令调度等相关阶段使用.Open64编译器框架采用了二次编译的方式设计机器描述文件的架构.在编译器后端的寄存器描述文件中增加复数运算的指令,对指令进行描述和注释.最终生成对应格式的汇编代码.魂芯DSP机器描述主要通过描述目标机器的指令格式信息、资源使用信息、延迟信息和指令信息来将目标机器的指令集[12]信息提供给编译器.机器描述的抽象表示主要由以下五个部分组成:

(1)SECTION opcode_desc描述了机制指令操作码;

(2)SECTION Operation_Format描述了源操作数和后的操作数的数后以及类型;

(3)SECTION Resource Usage描述资源使用信息;

(4)SECTION Table_Option描述资源选项;

(5)SECTION Scheduling_Alternative描述指令调度信息.

例如在机器描述文件中opcodes.knb文件中增加复数加法指令,opcode表示增加了复数加法的c4add机器描述,需要占用浮点ALU算术单元,这条指令的操作数描述码是112.操作数描述中,负号表示输入操作数,正号表示输出操作数,复数加法的指令表示有4个32位的浮点操作数,输出的是2个32位的浮点数.

opcode+=“230,c4add,fuALU,intel1,112,NULL”;

opndsgrp+=“112,?pr/OU_predicate,-fp32/OU_opnd1,-fp32/OU_opnd2,-fp32/OU_opnd3,-fp32/OU_opnd4,+fp32,+fp32”;

复数的加减和乘法都可以从过从CGIR在到指令注释的过程直接一一对应到魂芯DSP上的一条复数操作指令,但是魂芯DSP上并没有针对复数除法的单周期指令,针对复数除法必须利用一组指令的结合运算来得到最后的除法结果.根据第1节对复数除法的定义可以知道,要先算出除数的结果,利用魂芯DSP上特有的指令,我们知道这个平方和的结果就等于一个复数和他的共轭复数的乘积,利用魂芯DSP上特有的指令可以把复数的除法指令由原来的12条指令减少到只需要7条就可以完成.

3.4 Intrinsic技术识别实部和虚部

要在源代码级别识别复数的实部和虚部,可以通过intrinsic[13]技术,利用编译器把函数转换为汇编指令.intrinsic函数又称为built_in内建函数,是一种通过使用C函数方式来封装BWDSP底层系统结构的特殊汇编指令的编译器功能模块.编程人员可以通过使用C函数,编译器能够在内部将该C函数直接转换为指令系统所支持的一条或若干条高效的特殊汇编指令.通过将creal和cimag定义为intrinsic操作来在源码级获得复数类型的实部和虚部.复数虚部的实现结果如图5所示,把求复数虚部操作_image_f定义为一个F4INTRINSIC_OP操作.通过后端的指令注释可以直接得到复数的虚部,其实就是取代表复数寄存器对的较大序号的寄存器中的值.

4 实验结果

在完成了复数类型的支持和优化后,为了测试效果,选取了DSP经典的测试集[14]来测试编译器性能,测试是和以前编译器未针对复数类型进行优化的对比.在ECS(Effective Coding Studio)统计程序执行的周期数,程序优化前后执行的时钟周期数如表2所示.

涉及大量复数运算的是FFT和复数求点积算法,并行度比较高可以看出其加速比效果是原来的5～6倍,而复数求点和和规约求和因为本身数据并行度不大,优化效果是原来的2～3倍.至此,基于开源编译器框架Open64完成了针对魂芯DSP上新增复数类型为基础类型的开发.

优化复数支持后程序的加速比效果如图6所示,从图中可以看出,在完成编译器对复数类型的基本支持后,对复数程序的编译优化取得了较好的结果.相关算法的平均加速比达到了5.28倍.

图5 复数虚部intrinsic转换

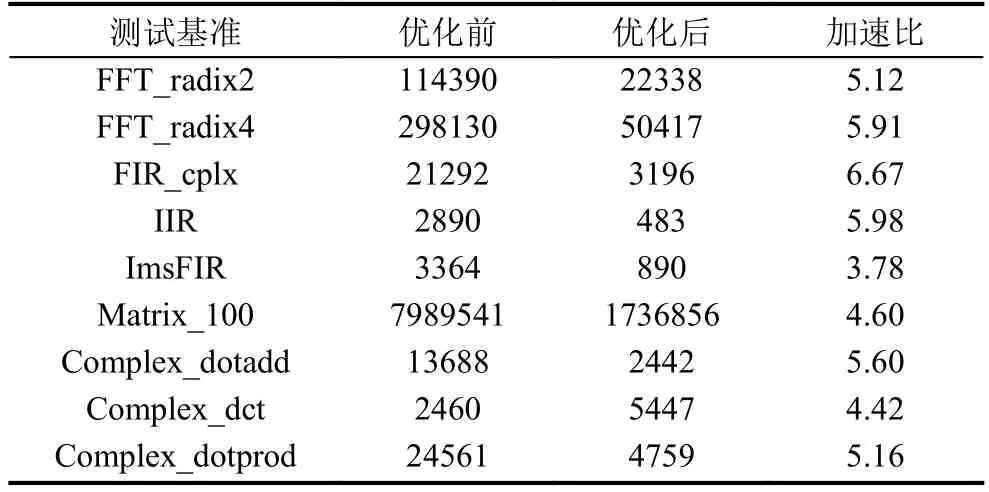
表2 优化前后的时钟周期数(cycles)

图6 编译器优化加速比

5 结语

本文针对魂芯DSP高性能处理芯片,利用其提供的复数运算指令,提出了32位复数数据类型作为编译器基础数据类型的模型,抽象出了复数作为编程基础数据类型具有的原子操作语义.基于开源的Open64编译器基础上,利用魂芯DSP特有的复数指令对复数操作进行了优化.通过对魂芯DSP芯片现有的高效的复数指令,提出了基于模式匹配的优化算法,此算法也可以通过扩展对其他的匹配模式进行优化.为了验证优化的效果,测试了编译器优化前后程序执行的时钟周期数,实验结果表明平均加速比为5.28.所提出的复数类型作为基础数据模型的一种通用增加数据模型的方法,以及基于模式匹配的优化算法也可以抽象推广到其他需要优化指令的平台.

1 CETC38TM.BWDSP100硬件用户手册.合肥:中国电子科技集团公司第三十八研究所,2011:1–2.

2 李欣,刘峰,龙腾.定点FFT在TS201上的高效实现.北京理工大学学报,2010,30(1):88–91.

3 王国栋,侯朝焕.GCC在高性能微处理器DSP和CPU上的移植.计算机工程与设计,2005,26(4):891–920.

4 Sui YL.Open64 introduction.http://www.cse.unsw.edu.au/～ysui/saber/open64.pdf.[2015-03-17].

5 Open64.Open64 compiler whirl intermediate representation.http://www.mcs.anl.gov/OpenAD/open64A.pdf.[2015-03-17].

6 CETC38TM.BWDSP100软件用户手册.合肥:中国电子科技集团公司第三十八研究所,2011:181–191.

7 丁陈飞,郑启龙,徐华叶,等.多簇超长指令字DSP复数运算的编译优化.计算机应用与软件,2015,32(2):14–17.

8 Cheong G,Lam MS.An optimizer for multimedia instruction sets.Proc.of the 2nd SUIF Compiler Workshop.Stanford,USA.1997.

9 黄胜兵,郑启龙,郭连伟.分簇VLIW DSP上支持单双字模式选择的SIMD编译优化.计算机应用,2015,35(8):2371–2374.[doi:10.11772/j.issn.1001-9081.2015.08.2371]

10 张军超.相连多寄存器组体系结构上的寄存器分配技术[博士学位论文].北京:中国科学院计算技术研究所,2005:92–94.

11 姜军,王超,尉红梅.一种局部寄存器分配的优化策略.计算机应用与软件,2013,30(12):215–217,254.[doi:10.3969/j.issn.1000-386x.2013.12.056]

12 王向前,洪一,王昊,等.魂芯DSP的编译器设计与优化.电子学报,2015,43(8):1656–1661.

13 Batten D,Jinturkar S,Glossner J,et al.Interaction between optimizations and a new type of dsp intrinsic function.Proc.of International Conference on Signal Processing Applications and Technology (ICSPAT’99).Orlando,Florida,USA.1999.

14 Živojnović V,Velarde JM,Schläger C,et al.DSPstone:A DSP-oriented benchmarking methodology.Proc.of International Conference on Signal Processing Applications and Technology (ICSPAT 1994).Dallas,USA.1994.

Complex Data Type Support and Optimization for BWDSP

WANG Yu-Lin,ZHENG Qi-Long,ZHAO Gao-Yi
1(School of Computer Science and Technology,University of Science and Technology of China,Hefei 230027,China)2(Anhui High Performance Computing Key Laboratory,University of Science and Technology of China,Hefei 230027,China)

BWDSP is a 32bit static scalar digital signal processor with VLIW and SIMD features,which is designed for high performance computing.In order to meet the performance requirements of digital high-performance computing,the soul core DSP provides a rich set of complex instructions,and the compiler cannot directly use these complex instructions to improve the compilation performance.Since BWDSP has a wealth of complex type of instructions,and it has high performance demands in the radar digital signal field,the implementation is researched according to the characteristics of BWDSP features based on the traditional open-source Open64 compiler framework to achieve the complex data type and complex operations support operations,and further optimization of complex instruction is realized by identifying a specific type of complex operation of a series of patterns.The experimental results show that the implementation on BWDSP compiler can achieve 5.28 time performance improvement on average.

compiler optimization;multi-cluster DSP;complex instructions;Open64 compiler

王玉林,郑启龙,赵高义.魂芯DSP上复数类型的支持和优化.计算机系统应用,2017,26(9):40–45.http://www.c-s-a.org.cn/1003-3254/5954.html

① 基金项后:“核高基”重大专项(2012ZX01034-001-001)

2016-12-28;采用时间:2017-01-18