用功能关系求解两物体的相关速度
陈明智
摘要:教学过程中常碰到相关速度的求解,在运动的合成与分解中这部分属于重点难点知识,一般情况下教师教学常用运动的分解解决相关速度,这个方法在一些案例中较难应用,本文主要从功能关系解决相关速度的问题。
关键词:能量守恒角度;内力做功角度;相关速度问题
同学们经常遇到这样一类问题:几个物体的运动存在着某种关系,根据其中一个物体的运动速度求其它物体的运动速度,这类问题称为相关速度问题。相关速度问题一般用以下三个结论:①刚性杆,绳上各点在同一时刻具有相同的沿杆、绳的分速度;②接触物系在接触面法线方向的分速度相同,切向分速度在无相对滑动时亦相同;③线状交叉物系交叉点是相交物系双方沿双方切向运动分速度的矢量和。
通常是将有关速度进行矢量分解,而根据平行四边形法则,一个速度矢量可以有无数多种分法,在这无数多种分法中应该选取哪一种,同学们是很感困难的,这对于同学们来说难度较大,不易理解和掌握。其实我们可以从功能角度分析相关速度问题,解题过程简捷且容易理解和掌握。现介绍如下:
一、从能量守恒角度分析相关速度问题
由轻绳、轻杆连结的物体,由于轻绳、轻杆的质量为零,根据能量守恒定律,其中一个物体对轻绳、轻杆的做功功率等于轻绳、轻杆对其它物体做功的功率。
例1:如图,一辆汽车通过一根跨过定滑轮的轻绳PQ提升井中质量为m的物体,设绳的总长度不变,定滑轮的质量和尺寸及滑轮上的摩擦不计,定滑轮距离地面的高度为H。开始时车(可看做质点)静止在A点,左右两侧绳都是绷紧且竖直的,提升时,车加速向左运动,沿水平方向从A经B驶向C,如图2所示,车过B点的速度为vB,此时绳与水平面的夹角为45°,求车由A驶到B的过程中,绳Q端的拉力对井中物体做的功?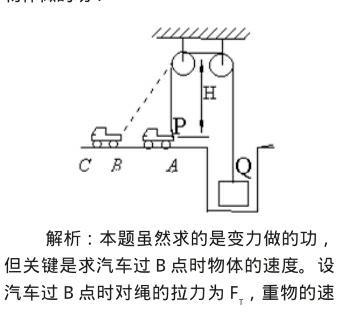

二、从内力做功角度分析相关速度问题
当两个相互关联的物体间的相互作用力是保守力时,即重力、弹力、万有引力以及静电力等。这一对作用力和反作用力做功的瞬时功率的代数和为零。
例2:如图所示,半圆型物体A水平向右运动,推动直杆B竖直向上运动,当半圆型物体A的速度大小为vA时,直杆B与物体A的交点和半圆型物体的圆心的连线跟水平方向成θ角,求此时直杆B的速度大小?
解析:设半圆型物体A与直杆B间相互作用的弹力大小为N,直杆B的速度大小为vB
直杆B对物体A的弹力做功瞬时功率为:P=NvAcosθ
物体A对直杆B的弹力做功瞬时功率为:P=NvBsinθ
由P=P, 得 vB=vA/tinθ。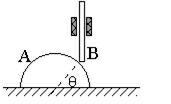
例3:如图,直杆OA在O处通过绞链固定,杆OA与地面间放有一高度为h的方木块,当OA杆以角速度ω顺时针匀速转动至与水平面成θ角时,木块运动速度多大?
解析:设OA杆与木块间相互作用的弹力大小为N,木块运动速度为v,OA杆与方木块的交点B的速度大小为: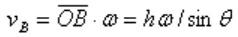
直杆对方木块的弹力做功瞬时功率为:P=Nvsinθ
方木块对直杆的弹力做功瞬时功率为:P=NvB=Nhω/sinθ
由P=P得, v=hω/sin2θ。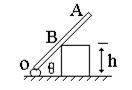
例4:如图,B是质量为mB,半径为R的光滑半球形碗, 放在光滑的水平桌面上。A是 质量为mA的细长直杆,被固定的光滑套管C约束在竖直方向,可自由上下运动。碗和杆 的质量关系为mB=2mA。初始时,A杆被握住,使其下端正好与碗的半球面的上边缘接触,如图。然后从静止开始释放A,A、B便开始运动.设A杆的位置用θ表示,θ为碗面的球心O至A杆下端与球面接触点的连接方向和竖直方向之间的夹角。求A与B的速度大小。
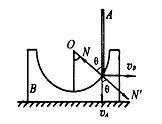
解析:取地面为参考系,任何时刻,A沿竖直方向运动,设其速度为vA,B沿水平方向运动,设其速度为vB,两者间仅存在法线方向弹力相互作用N和N,其中A杆所受弹力N对杆做功的瞬时功率大小为:P=NvAcosθ
碗所受弹力N 对碗做正功的瞬时功率大小为P=NvBsinθ
由P=P,得vA=vBtanθ。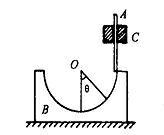
三、結语
轻绳、轻杆,以及两个相互关联的物体间的相互作用力是保守力,例如弹力时,他们都既不会提供能量,也不会消耗能量,其作用就是起到传递能量的作用,故任何时候输入功率与输出功率相等。从功能角度分析相关速度问题,本质上揭示物体之间的速度关系思路简捷,不易出错。并可加深对功和能的知识的认识和理解,有助于学生吃透相关速度问题,更有利于克服同学们的思维障碍,易于理解接受。
参考文献
[1] 袁孝金.浅谈绳系物体间的相关速度[J].中学立刻参考资料,1996.
[2] 百度文库.物体运动的相关速度,2014.
[3] 百度文库.求相关物体速度的一中有效方法,2015.endprint

