基于二次多项式回归模型的黑河流域TRMM数据降尺度研究

樊 东, 薛华柱, 董国涛, 蒋晓辉, 张文鸽, 殷会娟, 郭欣伟

(1.河南理工大学 测绘与国土信息工程学院, 河南 焦作 454000;2.黄河水利科学研究院 水利部黄土高原水土流失过程与控制重点实验室, 郑州 450003)

基于二次多项式回归模型的黑河流域TRMM数据降尺度研究

樊 东1,2, 薛华柱1, 董国涛2, 蒋晓辉2, 张文鸽2, 殷会娟2, 郭欣伟2

(1.河南理工大学 测绘与国土信息工程学院, 河南 焦作 454000;2.黄河水利科学研究院 水利部黄土高原水土流失过程与控制重点实验室, 郑州 450003)

在不同空间尺度下分别建立TRMM 3B43降水数据与数字高程模型(DEM)和归一化植被指数(NDVI)的二次多项式回归模型，将2001—2013年黑河流域TRMM降水数据的空间分辨率从0.25°提高到1 km，并利用流域内9个气象站点实测数据对降尺度结果进行了检验。结果表明：降尺度方法不仅提高了TRMM数据的空间分辨率，数据的精确程度也有所提高；与传统线性回归模型降尺度方法相比，基于二次多项式回归模型获得的降尺度结果更接近于实测值，其结果更为准确；模型建立的尺度对最终降尺度结果精确性具有较大影响，0.50°是基于DEM和NDVI对黑河流域TRMM降水数据进行降尺度的相对最优尺度。

TRMM数据降尺度; 二次多项式回归模型; DEM; NDVI; 黑河流域

降水是指地面从大气中获得水汽凝结物的总称。作为大气中最活跃的要素之一，降水的大小直接影响着地表的物质和水热循环，与气温气压、区域径流、植被生长以及人类工农业生产有着密切的联系。因此，准确并定量研究降水，特别是不同尺度降水的时空分布对于气候分析、区域水分循环、水量平衡、水资源评价、旱涝灾害管理和生态环境治理等都具有重要意义[1-2]。长期以来，降水数据依赖于地面雨量站的观测与收集[3]，空间化降水数据通常借助插值方法获取。但由于降水的高时空异质性，单个雨量站所获得的降水资料仅能表示其周围有限范围内的降水状况，受雨量站数量和分布影响难以准确反映出降水的时空分布规律[4-5]。基于卫星遥感的降水观测方式能有效克服地面观测站点数量不足和分布不均的问题，在全球范围内得到广泛应用，特别是对于地面雨量站相对缺乏地区[6]。与其他降水测量卫星相比，TRMM(Tropical Rainfall Measuring Mission)搭载了首个降雨雷达[7]，空间分辨率相对较高，达到0.25°，但在具体应用中其分辨率仍过于粗糙而不能满足某些研究需求[8]。为获取高时空分辨率的降水数据，一是发展更高分辨率的降水反演模式[9]，另一种方法则是降尺度[10]，由于提高降水反演模式难度较大，降尺度成为更可选的方法[11-12]。

Immerzeel等[13]研究发现植被的空间分布能较为有效地反映出降水的时空差异，并基于这种半经验关系建立了伊比利亚半岛TRMM降水数据与高分辨率NDVI之间的回归模型，将TRMM数据分辨率提高到1 km。Jia等[14]在此基础上引入地形信息建立了TRMM数据与NDVI和DEM的二元线性回归模型，提高了TRMM数据的空间分辨率。王超等[15]建立了TRMM数据与DEM的高次多项式回归模型，实现了对TRMM数据的降尺度。降尺度过程中，由于不同尺度下的降水量与地形、植被等预测因子之间的关系并不相同，因此不同建模尺度所得出的降尺度结果也会有所差异；同样，由于降水受地形、气候、纬度位置、海陆位置等因素影响，使得降水量与DEM，NDVI等预测因子间的关系存在时空上的不连续与非线性特征。王超等[15]通过融合高分辨率DEM获取了1 km分辨率的降水数据，但仅在单一尺度下建立多项式模型，没有考虑模型建立尺度对最终降尺度结果的影响；Jia等分别在4个不同尺度(0.25°，0.50°，0.75°和1.00°)下建立了TRMM数据和DEM，NDVI的统计回归模型，选择最优建模尺度用于最终降尺度过程，但是其基本假设是降水、高程和植被覆盖程度之间呈简单的线性关系，由于山区降水与高程之间关系的复杂性导致其降尺度结果精度仍有待提高。

为获取可靠的高分辨率降水数据，提高TRMM数据在黑河流域的空间分辨率与精度，本文基于Jia等[14]和王超等[15]提出的研究方法进行改进，将传统线性回归模型对高程进行二次展开，构建基于DEM和NDVI的二次多项式回归模型实现对山区降水模拟的逼近。同时，为研究模型建立尺度对降尺度结果精度的影响，分别在四个不同尺度下构建回归模型对2001—2013年黑河流域TRMM 3B43降水数据进行降尺度处理，并用同时期流域内9个气象站的实测降水量对降尺度结果进行验证。本研究一方面为黑河流域水文水资源过程分析获取高分率年降水数据，促进TRMM数据在黑河流域的应用；另一方面也为类似的低分辨率遥感降水数据降尺度，特别是地形变化较大的山区降水数据的降尺度提供参考实例。

1 研究区概况

黑河流域位于37°45′—42°40′N，96°42′—102°04′E，流域面积13万km2，是中国第二大内流区，地势南高北低，地形以山地和高原为主。流域上游为高山冰雪带和森林草原带，由于东南季风的影响导致其降水量相对较多，年平均降水超过350 mm；中游为河西走廊绿洲带，地形相对平坦，年均降水为200 mm左右；下游为阿拉善高原，降水通常不足50 mm，地表景观主要为荒漠，在河流沿岸有少量绿洲分布。流域内多年平均降水为168 mm(1960—2010年)，降水量年内分布表现为1—7月降水量逐渐增加，在7月达到最大值，之后逐渐减小，夏季降水量占全年降水量的58.29%。由于其干旱半干旱的气候条件和脆弱的生态环境，短缺的流域水资源成为控制整个流域生态平衡和社会经济发展的制约因素[16-18]。

2 数据和方法

2.1 数据与处理

2.1.1 数据来源 TRMM 3B43数据来源于美国NASA的Goddard数据分发中心，其空间范围为50°S—50°N，空间分辨率为0.25°×0.25°。DEM数据为SRTM (Shuttle Radar Topography Mission)DEM，空间分辨率为3″(约90 m)，数据格式为TIF。植被指数NDVI使用了搭载于Terra卫星上的中分辨率成像光谱仪(MODIS)提供的MOD13A2产品，时间分辨率为16 d，空间分辨率为1 km。实测降水数据来源于中国气象科学数据共享服务网，包含了流域内的9个国家基本和基准气象站2001—2013年的日降水数据。

2.1.2 数据处理 TRMM 3B43是月内平均每小时降水量，单位为mm/h，编程计算出每月降水量并将每月降水数据累加得到2001—2013年TRMM逐年降水量。研究[19-21]表明TRMM数据存在对降水高值的低估和低值的高估，式(1)(R2=0.84)是由流域内9个站点的实测降水量与其所在TRMM网格值所建立的回归函数，用来减少原始TRMM数据误差。

v=0.342u1.144

(1)

式中：u是TRMM 3B43获得的年降水量(mm)；v是9个气象站13年的年降水量观测值(mm)。

由于MOD13A2产品由16 d的NDVI所合成，根据其质量说明去除填充值，并通过最大值合成法获取2001—2013年每月NDVI，之后将年内NDVI取平均以代表该年的区域植被覆盖程度。此外，为去除人类农业活动导致的植被覆盖程度在空间上的不连续性，通过公式(2)计算每年NDVI的局部莫兰指数(Local Moran Index)，以排除降水量与植被覆盖程度不一致的区域。

(2)

式中：Ii为局部莫兰指数；xi为像元i的属性值；ωij为空间权重系数；n为像元个数。莫兰指数是探测空间变异的有效手段[14,22]，空间上过于集聚和孤立的区域表现为莫兰指数小于0，故排除莫兰指数小于0的像元，其像元值由周围像元通过普通克里金法内插得到。

STRM DEM空间分辨率为3″，为保证与其他数据空间分辨率的统一，将其重采样到1 km，采样方法为最邻近元法。

2.2 降尺度方法

随着时间尺度的增大，地形和植被通常能有效地指示降水的空间分布状况。本文以高程表示区域地形信息、以NDVI表示区域植被信息，则降水的空间分布模型可以表示为：

P=F(X,Y)+ε

(3)

式中：P为某时段内的降水量；X为高程所代表的地形信息；Y为由NDVI表示的植被信息；ε为残差，它表示不能由地形和植被有效指示的那部分降水量。考虑到山区降水会存在最大或最小高程带，并针对传统的线性模型在山区降水模拟精度较低的情况，对高程进行二次展开：

P=aX2+bX+cY+d+ε

(4)

式中：a，b，c分别为各变量的系数；d为常数项；ε为残差。

不同尺度下地形、植被和降水量之间的关系是不同的[13-14]。同样，不同尺度下建立的回归函数所得到的降尺度结果也不相同，故分别在四个不同尺度下(0.25°，0.50°，0.75°和1.00°)建立二次回归模型，分析模型建立尺度对降尺度结果精度的影响。具体步骤为：

(1) 分别在四个不同尺度下提取TRMM，DEM和NDVI对应像元值P，X，Y，由最小二乘法求出式(4)中的各变量系数a，b，c和常数项d。

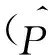
(5)

(3) 用简单张力样条函数法将残差(ε)内插为1 km分辨率。

(4) 根据所得的各变量系数a，b，c，d及1 km分辨率下的DEM和NDVI求出1 km分辨率的降水量模拟值，最后加上1 km分辨率下的残差值便可将TRMM数据的空间分辨率由0.25°降尺度至1 km。

2.3 验证方法

气象站实测降水数据虽呈离散点状，但其仍然是对降水最直接的观测结果，本文通过计算2001—2013年的TRMM数据降尺度结果与同时期9个气象站所获得的实测降水量的决定系数(R2)、偏差(Bias)和均方根误差(RMSE)来对降尺度方法的有效性进行验证，计算方法为：

(6)

(7)

(8)

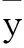
3 结果与分析

3.1 降尺度结果与验证

3.1.1 降尺度结果 图1为TRMM数据降尺度的实现过程(以2013年为例)。图1A是原始分辨率下黑河流域2013年的TRMM降水数据，可明显地看出流域内降水量随海拔的降低由南向北呈现明显的递减趋势，2013年流域上游山区降水量均超过250mm，而到中下游降水量迅速降低到150mm以下。图1B，E是将DEM和NDVI带入二次回归函数所求得的不同分辨率的降水模拟值，可以看出模拟降水量的空间分布与TRMM原始数据具有较高的一致性。图1C，D是不同分辨率下的降水量残差，它代表了不能由地形和植被覆盖模拟出的那部分降水量。图1F为最终的降尺度结果，它是由高分辨率的降水模拟值和降水残差值相加得到。对比图1A和图1F可以发现，二者的降水空间分布趋于一致且降水量均在0～600mm；在空间分辨率方面，相对于原始的TRMM降水数据，降尺度结果的空间分辨率有很大提高，达到1km。

图1TRMM降水量、模拟降水量、残差和降尺度结果

3.1.2 精度验证 黑河流域2001—2013年的TRMM降水数据通过降尺度处理后数据的空间分辨率有很大提高，但降尺度结果的精确性还有待检验。本文利用流域内的9个站点的日降水实测数据对降尺度结果进行了验证。通过提取各站点处的原始TRMM数据和降尺度后的像元值分别与实测降水量做线性回归分析，结果见图2。由图2A可以看出，原始TRMM像元值多分布与1∶1线之上，存在对降水的明显高估。经过降尺度处理后的对应像元值与实测降水量散点图(图2C)更接近于1∶1线，与实测值有着更高的一致性。进一步计算实测值与对应像元值的决定系数(R2)、偏差(Bias)和均方根误差(RMSE)(表1)可以发现，与原始TRMM数据相比，降尺度结果与实测降水的决定系数提高了0.05，偏差减小了0.27，均方根误差降低了38.23 mm。因此，降尺度结果不仅提高了TRMM数据的空间分辨率，而且较为有效地提高了数据的准确性。

3.2 与传统模型的精度比较

为比较传统线性回归模型(LRM)与二次多项式回归模型(QPRM)TRMM数据降尺度效果，本文同时采用了传统线性回归模型对TRMM数据进行降尺度，并用实测降水数据对降尺度结果进行了验证，结果如图2B和表1所示。对比两种降尺度模型的降尺度结果，基于DEM展开的二次多项式回归模型表现出更高的决定系数、更小的偏差和均方根误差，其精度优于传统的线性模型。主要原因在于，流域上游祁连山地的存在使东南季风受到地形的抬升作用导致降水随海拔的增高逐渐增大，到达一定高程(4 000 m)后，随着大气水汽含量的逐渐降低，降水量随海拔的增高而逐渐减小(图3)。此过程可以很好地被二次函数所模拟，因此改进的降尺度模型能获得更为精确的降尺度结果。

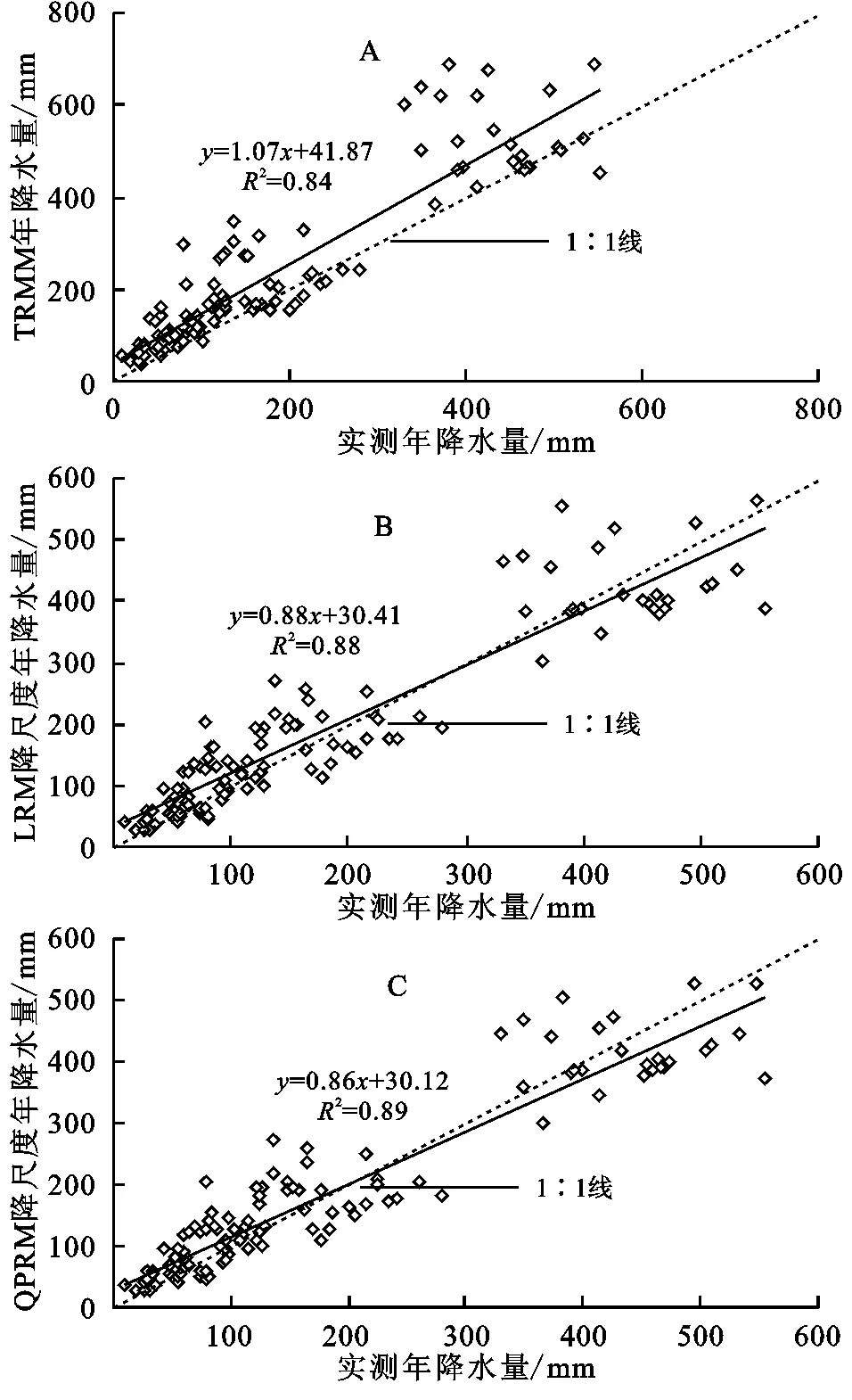
图2 TRMM数据、LRM降尺度数据、QPRM降尺度

参数TRMMDSLRMDSQPRMR20.840.880.89Bias0.300.050.03RMSE/mm90.1954.3451.96

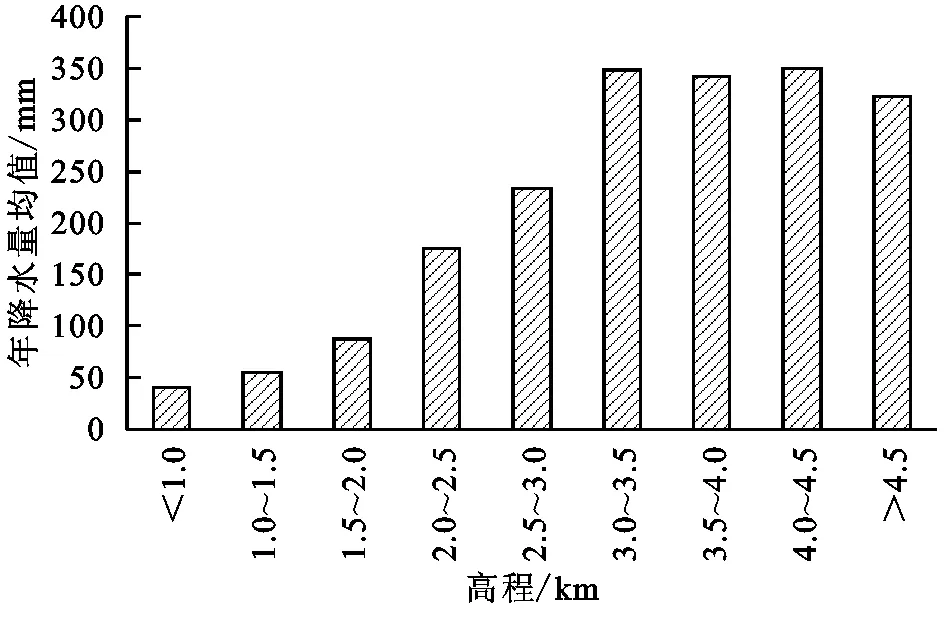
图3黑河流域不同高程带降水特征

3.3 不同建模尺度对结果精度的影响

为研究回归模型建立尺度对降尺度结果的影响，本文分别利用四个不同尺度下建立的回归模型对2001—2013年黑河流域TRMM降水数据进行降尺度，并计算了降尺度结果与实测数据的决定系数(R2)、偏差(Bias)和均方根误差(RMSE)(表2)。综合各项指标可以发现，在0.50°下建立的降尺度模型与实测降水量有更好的一致性。究其原因，在于模型建立尺度过小时，小范围的地形起伏和植被分布不能准确地反映降水量的多少；而在尺度过大时，地形起伏和植被分布对降水的指示作用又不够明锐。

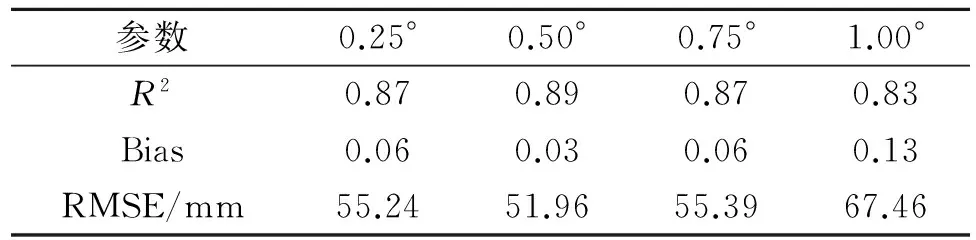
表2 2001-2013年不同建模尺度的降尺度结果在9个站点的验证

4 结 论

(1) 基于高分辨率DEM和NDVI的黑河流域TRMM 3B43降水数据统计降尺度方法能极大地提高数据空间分辨率，并有效改善数据质量提高数据精确性。

(2) 基于DEM展开的二次多项式模型能在一定程度上解决传统线性降尺度模型在地形起伏较大时对降水量模拟精度不高的问题，使得降尺度结果与实测降水量有更高的一致性。

(3) 降尺度模型建立的尺度对降尺度结果精度具有较大影响，0.50°是利用区域地形和植被信息模拟黑河流域降水空间分布的相对最佳尺度。

本文对黑河流域TRMM降水数据的降尺度方法仍然存在许多不足。文中使用了DEM和NDVI两个较为常见且易于获得的降水量指示因子来对TRMM数据进行了降尺度，而温度、湿度、气压等变量可能会对降水的空间分布有着更高的模拟效果[23]。此外，对整个研究区采用了相同的降尺度系数，实际上由于地表的复杂性，降水量与高程、植被之间的关系受到水文条件、人类活动因素的影响可能会随着空间位置的不同而不同，这将是下一步重点研究和探讨的方向。

致谢：感谢NASA提供的TRMM 3B43，MODIS 13A2和DEM数据；感谢中国气象数据共享中心提供的气象数据；感谢黑河计划数据管理中心提供的流域基础数据。

[1] 吕洋,杨胜天,蔡明勇,等. TRMM卫星降水数据在雅鲁藏布江流域的适用性分析[J].自然资源学报,2013,28(8):1414-1425.

[2] Xu G, Xu X, Liu M, et al. Spatial downscaling of TRMM precipitation product using a combined multifractal and regression approach:demonstration for south China[J]. Water, 2015,7(6):3083-3102.

[3] Goodrich D C, Faurès J M, Woolhiser D A, et al. Measurement and analysis of small-scale convective storm rainfall variability[J]. Journal of Hydrology, 1995,173(1):283-308.

[4] 孙乐强,郝振纯,王加虎,等. TMPA卫星降水数据的评估与校正[J].水利学报,2014,46(10):1135-1146.

[5] Wilheit T T. Some comments on passive microwave measurement of rain[J]. Bulletin of the American Meteorological Society, 1986,67(10):1226-1271.

[6] Fang J, Du J, Xu W, et al. Spatial downscaling of TRMM precipitation data based on the orographical effect and meteorological conditions in a mountainous area[J]. Advances in Water Resources, 2013,61(1):42-50.

[7] Huffman G J, Bolvin D T, Nelkin E J, et al. The TRMM Multisatellite Precipitation Analysis(TMPA): quasi-global, multiyear, combined-sensor precipitation estimates at fine scales[J]. Journal of Hydrometeorology, 2007,8(1):38-55.

[8] Su F, Hong Y, Lettenmaier D P. Evaluation of TRMM Multisatellite Precipitation Analysis(TMPA)and its utility in hydrologic prediction in the La Plata Basin[J]. Journal of Hydrometeorology, 2007,9(4):622-640.

[9] 刘元波,傅巧妮,宋平,等.卫星遥感反演降水研究综述[J].地球科学进展,2011(11):1162-1172.

[10] 范丽军.统计降尺度方法的研究及其对中国未来区域气候情景的预估[D].北京:中国科学院研究生院,2006.

[11] Park N. Spatial downscaling of TRMM precipitation using geostatistics and fine scale environmental variables[J]. Advances in Meteorology, 2013,13(11):187-190.

[12] Guan H, Wilson J L, Xie H. A cluster-optimizing regression-based approach for precipitation spatial downscaling in mountainous terrain[J]. Journal of Hydrology, 2009,375(3):578-588.

[13] Immerzeel W W, Rutten M M, Droogers P. Spatial downscaling of TRMM precipitation using vegetative response on the Iberian Peninsula[J]. Remote Sensing of Environment, 2009,113(2):362-370.

[14] Jia S, Zhu W, Lv A, et al. A statistical spatial downscaling algorithm of TRMM precipitation based on NDVI and DEM in the Qaidam Basin of China[J]. Remote Sensing of Environment, 2011,115(12):3069-3079.

[15] 王超,赵传燕. TRMM多卫星资料在黑河上游降水时空特征研究中的应用[J].自然资源学报,2013,28(5):862-872.

[16] 康尔泗.寒区和干旱区水文研究的回顾和展望[J].冰川冻土,1998,20(3):238-242.

[17] 程国栋,赵传燕.干旱区内陆河流域生态水文综合集成研究[J].地球科学进展,2008,23(10):1005-1012.

[18] 侯兰功,肖洪浪,邹松兵,等.黑河流域水循环特征研究[J].水土保持研究,2010,17(3):254-258.

[19] Liu J, Zhu A, Duan Z. Evaluation of TRMM3 B42 precipitation product using rain gauge data in Meichuan Watershed, Poyang Lake Basin, China[J]. Journal of Resources and Ecology, 2012,3(4):359-366.

[20] Li Z, Yang D, Hong Y. Multi-scale evaluation of high-resolution multi-sensor blended global precipitation products over the Yangtze River[J]. Journal of Hydrology, 2013,500(14):157-169.

[21] Peng B, Shi J, Ni-Meister W, et al. Evaluation of TRMM Multisatellite Precipitation Analysis(TMPA)products and their potential hydrological application at an arid and semiarid basin in China[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014,7(9):3915-3930.

[22] Zhang X, Hu Y, Zhuang D, et al. NDVI spatial pattern and its differentiation on the Mongolian Plateau[J]. Journal of Geographical Sciences, 2009,19(4):403-415.

[23] Spak S, Holloway T, Lynn B, et al. A comparison of statistical and dynamical downscaling for surface temperature in North America[J]. Journal of Geophysical Research:Atmospheres, 2007,112(8):271-283.

DownscalingStudyonTRMM3B43DataoftheHeiheRiverBasinBasedonQuadraticPolynomialRegressionModel

FAN Dong1,2, XUE Huazhu1, DONG Guotao2, JIANG Xiaohui2,ZHANG Wenge2, YIN Huijuan2, GUO Xinwei2

(1.SchoolofSurveyingandLandInformationEngineering,HenanPolytechnicUniversity,Jiaozuo,He′nan454000,China; 2.KeyLaboratoryofSoilandWaterLossProcessandControlontheLoessPlateau,MinistryofWaterResources,YellowRiverInstituteofHydraulicResearch,Zhengzhou450003,China)

Precipitation data with high accuracy and high spatial resolution are important to ecology, hydrology and meteorology. In this study, we established a Quadratic Polynomial Regression Model (QPRM) between TRMM 3B43 precipitation, Digital Elevation Model (DEM) data and Normalized Difference Vegetation Index (NDVI) on four different scales (0.25°, 0.50°, 0.75° and 1.00°), and the TRMM 3 B430.25°×0.25° precipitation fields were downscaled to 1 km×1 km for each year from 2001 to 2013. The downscaled precipitation estimates were subsequently validated against the in-situ observation data obtained from nine rain gauge stations in the period of 13 years in the Heihe River Basin. The results showed that both spatial resolution of data and the data quality were significantly improved. Compared with multiple linear regression model downscaling method, the downscaled result obtained by QPRM is more accurate and closer to the measurements from rain gauges. The modeling scale has a great influence on the accuracy of the downscaled results, and 0.50° is the optimal scale to obtain high spatial resolution precipitation by downscaling TRMM 3B43 products using DEM and NDVI data.

downscaling of TRMM data; quadratic polynomial regression model; DEM; NDVI; Heihe River Basin

2016-03-31

：2016-05-07

国家自然科学基金(91325201,41301496,41301030);水利部公益性行业科研专项经费项目(201401031)

樊东(1992—),男,四川宜宾人,硕士研究生,研究方向为3S技术理论与应用。E-mail:fan_zhonghe@163.com

董国涛(1982—),男,山东青州人,博士,高级工程师,主要从事水文水资源遥感方面研究。E-mail:dongguotao@hky.yrcc.gov.cn

P332.1

：A

：1005-3409(2017)02-0146-06