沃尔什哈达玛变换域的无参考图像质量评价*
侯春萍,刘月,岳广辉,冯丹丹,马彤彤
(天津大学 电气自动化与信息工程学院,天津 300072)
沃尔什哈达玛变换域的无参考图像质量评价*
侯春萍,刘月,岳广辉†,冯丹丹,马彤彤
(天津大学 电气自动化与信息工程学院,天津 300072)
图像失真会改变图像低频成份和图像高频成份的统计信息,基于这种特性,提出了一种新颖的无参考混合失真图像质量评价方法.首先对图像进行局部沃尔什哈达玛变换,将空域图像转换为局部沃尔什哈达玛变换图;然后在局部沃尔什哈达玛变换图上进行特征提取,即分别提取反映图像低频成份的零列率项和反映图像高频成份的非零列率项的旋转不变局部二值模式统计特征;最后利用支持向量回归网络训练特征,获得特征到质量分数的映射关系模型.在两个混合失真数据库(MLIVE数据库和MDID2013数据库)上对所提出的算法进行性能验证,实验结果表明,提出的算法具有很好的主客观评价一致性,性能优于目前现有较优秀的全参考图像质量评价算法和无参考图像质量评价算法.
图像质量评价;无参考;局部沃尔什哈达玛变换;局部二值模式;支持向量回归
图像质量评价是图像处理研究中的热点问题之一,对图像质量评价的研究,可以有效地用于图像视频的优化问题,如传输[1]、压缩、亮度提升[2]、对比度增强、色阶映射、去雾等.近年来,随着图像质量评价研究的不断深入,涌现了大量优秀的单失真图像质量评价算法[2-4].然而,图像在获得、传输、压缩、存储时会引入多种失真,所以研究混合失真图像质量评价方法具有非常重要的现实意义.研究者针对这种现象提出了相应的混合失真图像质量评价算法.Gu等[5]通过模拟人类视觉系统质量评价过程,将多种失真分开考虑和估计,最后加权估计分数得到最终的图像质量分数;在此基础上,Gu等[6]又加入了自由能解释多种失真的联合效应;Li等[7]通过提取反映图像失真程度的相位一致性、灰度共生矩阵等多种特征,利用SVR建立特征到质量分数的映射关系,评价多失真图像的质量;Lu等[8]选择性地选取对失真敏感的特征,采用改进的Bag-of-word编码特征,最后通过简单的线性加权实现了特征到质量分数的映射.Chandler[9]指出混合失真图像质量评价算法不仅需要考虑单个失真对图像质量的影响,还需考虑多种失真之间的相互作用和联合效应对图像总体质量的影响.综上所述,混合失真图像质量评价处于刚刚起步的阶段,现有算法主要是基于对特定失真类型及失真之间相互影响的分析.因此,提出一种不针对特定失真类型的图像质量评价算法迫在眉睫.
本文针对混合失真图像质量评价问题,提出了一种基于沃尔什哈达玛变换的混合失真图像质量评价方法.本算法不需要关于图像失真类型的先验信息,其性能优于目前现有较优秀的算法.
1 沃尔什哈达玛变换
图像变换是一种重要的图像处理方法,在图像质量评价领域有着广泛的应用.常用的图像变换方法有很多,如离散傅里叶变换、小波变换[10-11]、离散余弦变换、K-L变换、WHT.其中,离散傅里叶变换以复指数函数为基函数;小波变换以母小波经过伸缩和平移变换后派生出的函数族为基函数;K-L变换以协方差矩阵的特征向量为基函数;离散余弦变换以余弦函数为基函数;而WHT以一组取值为±1的完备正交矩形波为基函数,使得WHT较其它变换简单.
给定一幅图像,其LWHT由图像所有重叠块经沃尔什哈达玛变换矩阵(Walsh Hadamard Transfrom matrix,WHTM)变换实现.WHTM由哈达玛矩阵按照一定规律排列得到,式(1)表示最低二阶哈达玛矩阵,由二阶哈达玛矩阵H2的克罗内克积递推可得到N阶哈达玛矩阵HN:
(1)

(2)
式中:N表示哈达玛矩阵的阶数.
重排哈达玛矩阵,计算N阶哈达玛矩阵每行±1符号改变次数,符号改变次数称为列率,将哈达玛矩阵按照列率递增的顺序排列即可得到WHTM.以四阶WHTM为例:

(3)
式中:矩阵旁数字0,1,2,3为四阶哈达玛矩阵的列率.
WHTM的每一行称为一维沃尔什哈达玛基向量Vj,j=0,1,…,N-1.由一维沃尔什哈达玛基向量的张量积可以得到二维沃尔什哈达玛变换核[12]g(x,y,u,v)(WalshHadamardTransformkernels,WHTK),公式如下:
(4)
式中:T表示矩阵转置,x,y=0,1,…,N-1;u,v=0,1,…,N-1;i=1,2,…,N×N.WHTK如图1所示.从图中可以发现,主对角线以上的WHTK是主对角线以下的WHTK的转置.w1=g(x,y,0,0) 表示左上角的沃尔什哈达玛变换零列率核,其余变换核为沃尔什哈达玛变换非零列率核.
定义图像的LWHT为图像所有重叠块在WHTK上的投影,将投影后得到的矩阵称为沃尔什哈达玛投影矩阵.图像在沃尔什哈达玛变换零列率核上的投影称为零列率项,在沃尔什哈达玛变换非零列率核上的投影称为非零列率项,零列率项和非零列率项统称为局部沃尔什哈达玛变换图[13].大小为N×N的图像块f(x,y)在WHTK上的投影公式如下:

(5)
式中:(x,y)表示图像块像素点的坐标,x,y=0,1,…,N-1(通常N为2的整数次幂,N=2n);H(u,v)表示沃尔什哈达玛变换值.
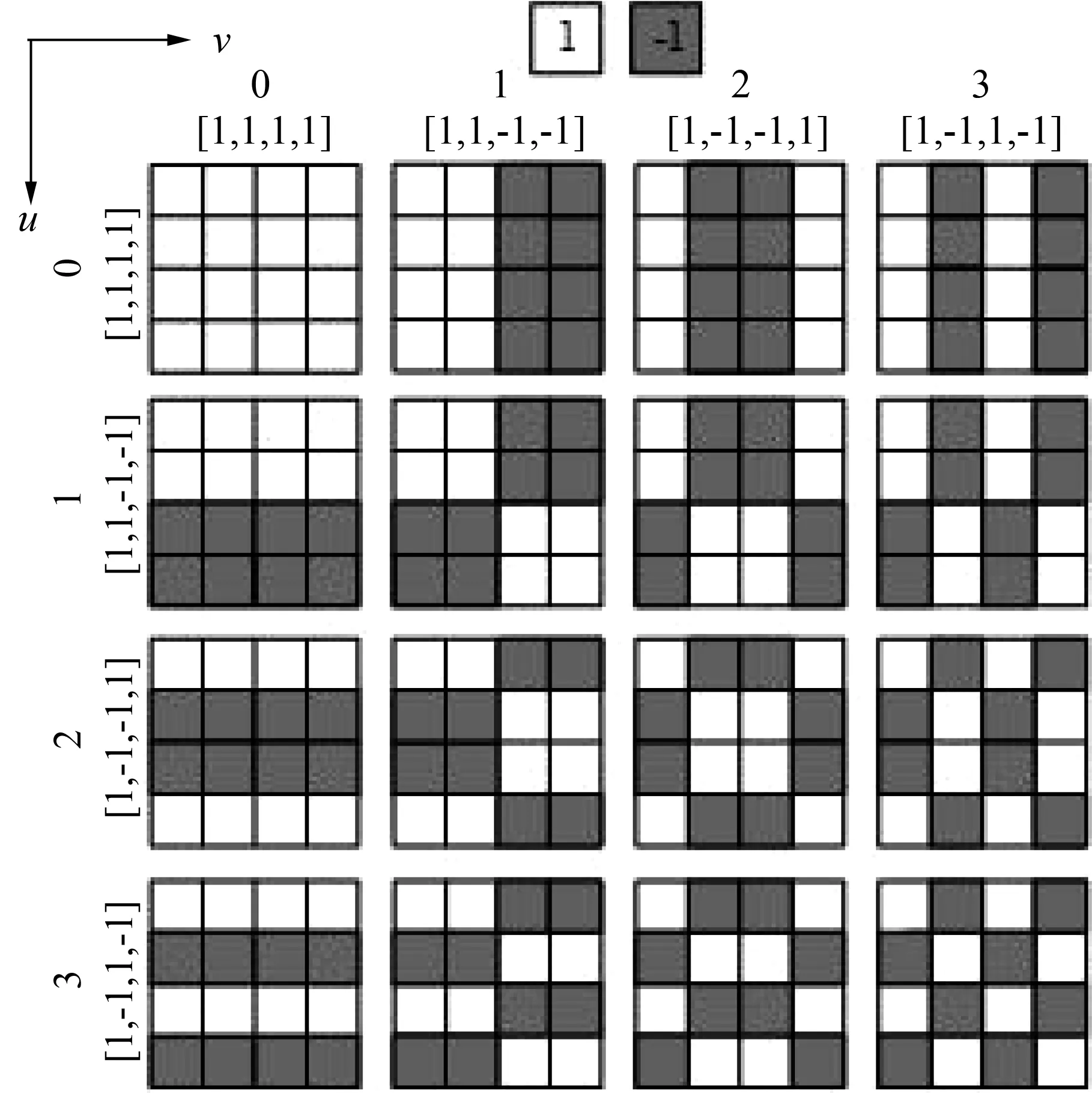
图1 沃尔什哈达玛变换核Fig.1 Walsh Hadamard Transform kernels
2 局部二值模式
LBP是一种描述图像局部纹理特征的算子,同时也是一种有效的统计算子,广泛地应用在人脸识别上[14].原始LBP算子定义在大小为3×3的矩形窗口内,以窗口中心像素灰度值为阈值,将邻域8个像素灰度值与中心像素灰度值进行比较,若邻域像素灰度值大于或等于中心像素灰度值,该邻域像素点标记为1,否则标记为0,经比较可产生8位二进制数(通常转换为十进制数,共有256种模式),即为该窗口中心像素点的LBP值,如图2所示.
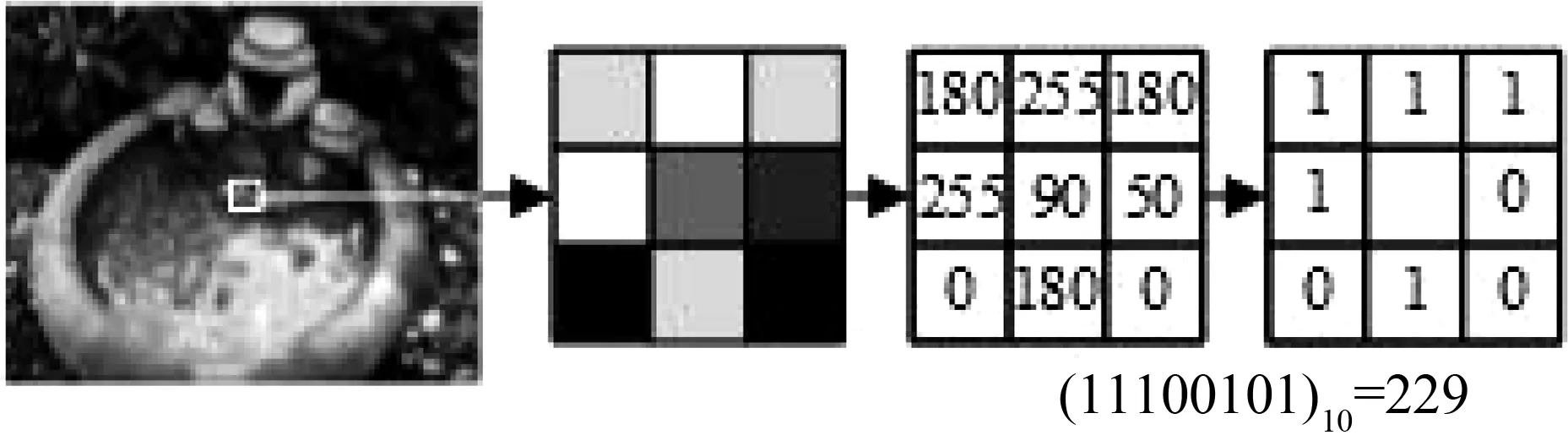
图2 原始LBP算子Fig.2 Original local binary pattern operator
原始LBP算子编码形式如下:
(6)
(7)
式中:tc为中心像素灰度值;ti为邻域像素灰度值;P为邻域像素点数;R为邻域半径;q(·)为阈值函数.
随着对LBP研究的不断加深,区域由原来的矩形区域变为圆形区域,固定半径变为可变半径,如图3所示,相继出现了均匀模式和旋转不变LBP[15].旋转不变LBP模式种类减少至P+2种,编码公式如下:

图3 几种LBP算子Fig.3 Several local binary pattern operators
U(LBPP,R)=‖q(tP-1-tc)-q(t0-tc)‖+
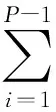
(8)
(9)
式中:U表示0,1跳变次数;riu2表示0,1跳变次数不超过2次的旋转不变LBP.利用旋转不变LBP编码大小为M1×M2图像的每一个像素点,即可得到旋转不变LBP图,通常用旋转不变LBP图的统计直方图表示图像的纹理信息和统计信息,定义如下:
(10)
(11)

(12)
式中:k∈[0,K]表示旋转不变LBP的不同编码模式;K表示旋转不变LBP的不同编码模式总数.
3 特征提取
特征提取是图像质量评价算法的关键部分,决定图像质量评价算法的好坏,本文提出了一种应用LWHT进行特征提取的方法,实现了较好的性能.
图像的WHT具有多种有用的性质:
1)零列率项测量图像的亮度信息.
(13)
2)空域能量和沃尔什哈达玛变换域能量守恒.
(14)
3)能量压缩特性.图像经WHT后,大部分的能量被压缩到少数几个沃尔什哈达玛变换值中,这几个沃尔什哈达玛变换值相对于其它的沃尔什哈达玛变换值具有更重要的意义.
图像变换可以分离出图像的不同频率成份[16],图像的低频成份对应图像的亮度特征,而图像的高频成份对应图像的边缘特征;由第一条变换性质可知,零列率项测量图像的亮度信息,所以可以从零列率项的统计特性中获得图像的亮度特征;由空域和沃尔什哈达玛变换域能量守恒可以得出,图像变换前后能量不变.图像经WHT变换后分成零列率项和非零列率项,零列率项对应于图像的低频成份,所以非零列率项对应于图像的高频成份.对于不同失真程度的图像,低频成份和高频成份衰减程度不同,对应低频成份的零列率项和对应高频成份的非零列率项的统计特性自然也不同.本文通过利用这些WHT性质进行特征提取,同时通过实验证明了算法采用四阶WHT性能最好,在实验结果部分进行了验证.
根据LWHT的定义可知,一幅图像经四阶WHT后将得到16幅局部沃尔什哈达玛变换图,其中一幅为零列率项,另外15幅为非零列率项.图4给出了一幅图像的16幅局部沃尔什哈达玛变换图.
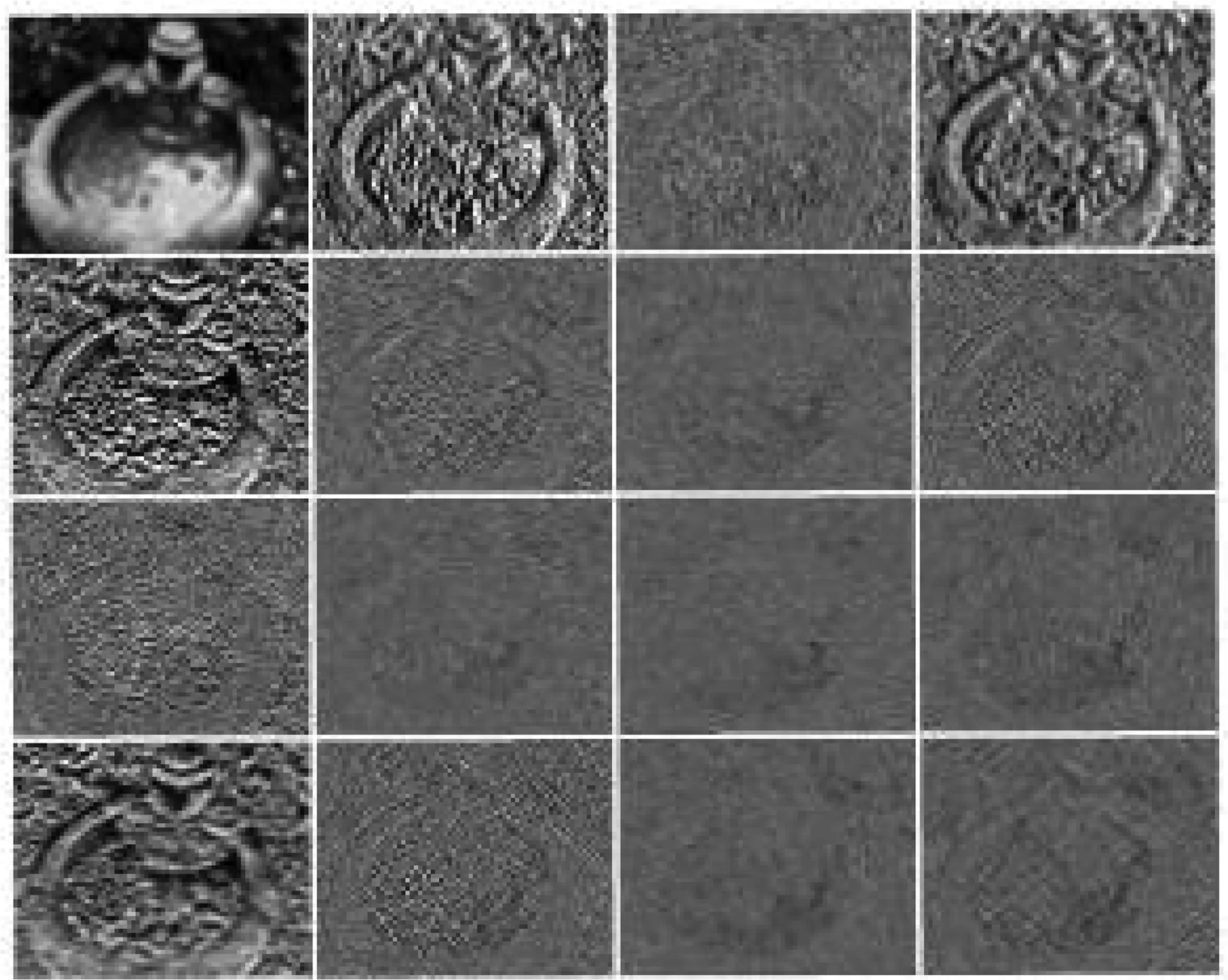
图4 局部沃尔什哈达玛变换图Fig.4 Local Walsh Hadamard Transform maps
从图4中可以发现,零列率项(左上角第1幅图)保留了图像的亮度信息,非零列率项保留了图像的边缘信息.由于图像灰度值分布越均匀,图像经WHT后,能量越集中在沃尔什哈达玛投影矩阵的边角上,而且任意两个非零列率项都足以表达图像的高频特性,所以本文为了降低冗余并没有在所有的局部沃尔什哈达玛变换图上进行特征提取,而是选择在唯一的零列率项和两个非零列率项上进行特征提取.从图像在w5=g(x,y,1,0)和w6=g(x,y,1,1)两个沃尔什哈达玛变换非零列率核上的投影中提取图像边缘信息,在w1=g(x,y,0,0)沃尔什哈达玛变换零列率核上的投影中提取图像的亮度信息.
(15)
-1,-1,-1,-1]
(16)
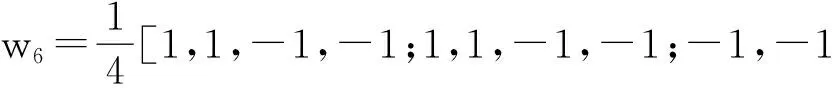
1,1;-1,-1,1,1]
(17)
对于一幅给定的大小为M1×M2的彩色图像,首先将其转换为灰度图像,然后计算灰度图像的四阶WHT.设Zm={z1m,z2m,z3m},m=1,2,…,M1×M2表示第m个大小为4×4的图像块Bm在w1,w5,w63个WHTK上的沃尔什哈达玛变换值,计算公式如下:
(18)
(19)
(20)
式中:·*表示卷积.图5列举了1幅图像利用本算法提取的3幅特征图,其中第1幅特征图是零列率项,第2幅和第3幅特征图是非零列率项.

图5 3幅局部沃尔什哈达玛变换图Fig.5 Three local Walsh Hadamard Transform maps
由于人类视觉系统具有多尺度分解的特点,图像的不同尺度对算法性能有影响,本文利用因子为2的下采样实现了多尺度[17],通过实验证明算法采用三尺度时性能最好.又由于从零列率项和非零列率项的统计特性中分别可以提取图像的亮度信息和边缘信息,而旋转不变LBP算子是一种有效的统计算子,所以本文在3个尺度上分别对零列率项和非零列率项应用R=1,P=8的旋转不变LBP算子进行图像特征提取.本文提出的算法的总体实现框图如图6所示.
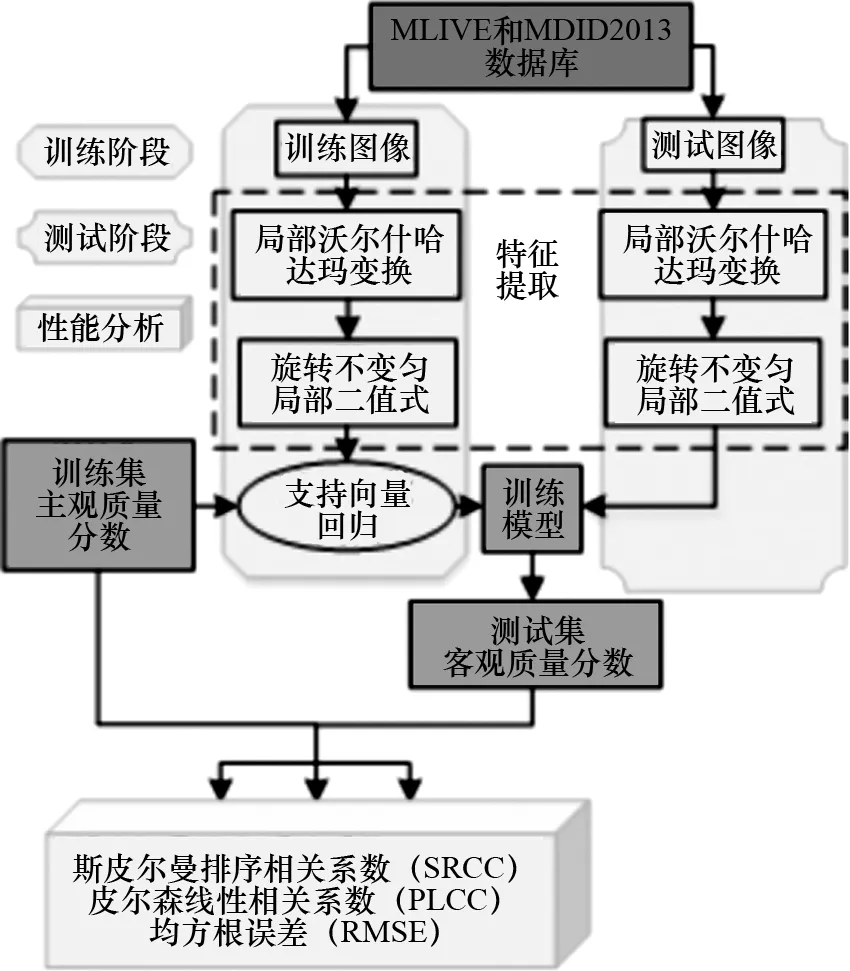
图6 算法流程图Fig.6 Flow chart of the proposed method
4 实验结果及性能分析
4.1 数据库和评价指标介绍
目前,主要的混合失真数据库有MLIVE[18]和MDID2013[5]两种.MLIVE数据库包含两个子集,每个子集包含15幅参考图像及其相应的225幅不同程度的失真图像;MDID2013数据库包含12幅参考图像及其相应的324幅不同程度的失真图像.数据库具体信息见表1.
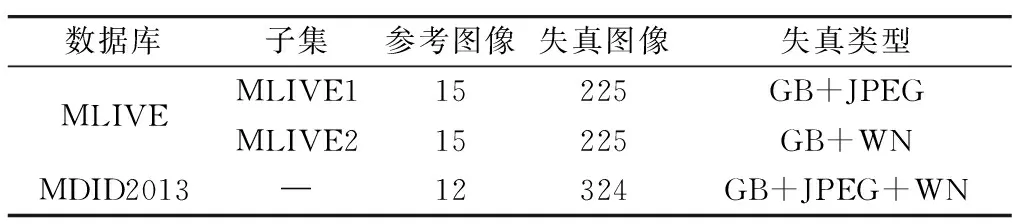
表1 数据库信息Tab.1 Database information
国际上常用的衡量客观图像质量评价算法性能的指标有:斯皮尔曼排序相关系数(Spearman rank-order correlation coefficient,SRCC)、皮尔森线性相关系数(Pearson linear correlation coefficient,PLCC)和均方根误差(root-mean-squared error,RMSE).PLCC和RMSE指标衡量客观算法的预测准确性,SRCC指标衡量客观算法的预测单调性.PLCC和SRCC的值越接近1,RMSE的值越小,说明算法性能越好,图像客观预测质量分数与主观质量分数相关性越高.为了减少非线性因素对算法性能的影响,本文在计算PLCC和RMSE时采用5参数的Logistic函数[19]对主、客观评价分数进行非线性回归,Logistic函数公式如下:
Q(x)=u1logistic(u2,(x-u3))+u4x+u5
(21)
(22)
式中:ui,i=1,2,…,5表示拟合参数.
4.2 模型建立
本文分别基于两个混合失真数据库,利用SVR网络构建无参考图像质量评价模型,测试了所提算法的性能,主要借助台湾大学林智仁博士等开发设计的LIBSVM工具包.无参考图像质量评价模型采用ε-SVR回归支持向量机,核函数采用径向基函数,具体模型建立和算法测试步骤如下:
1)随机选取每个数据库中80%的图像作为训练集,其余20%的图像作为测试集.
2)利用SVR网络对训练集图像的特征及其对应的主观质量分数进行训练,获得特征到主观质量分数的映射关系模型;再利用得到的关系模型对测试集图像的质量进行预测.计算预测客观质量分数与主观质量分数的SRCC,PLCC和RMSE的值.
3)重复1),2)过程1 000次,取1 000次测试得到的SRCC,PLCC和RMSE值的中值作为最终的性能,用于算法性能比较.
4.3 算法性能比较和分析
本文通过性能比较,验证提出算法的有效性.表2给出了本文提出的算法与一些优秀的全参考图像质量评价(full-reference image quality assessment,FR-IQA)算法和无参考图像质量评价(no-reference image quality assessment,NR-IQA)算法的性能比较结果.FR-IQA算法包括PSNR,SSIM[3],VSNR[20],VIF[21],FSIM[22],GMSD[23];NR-IQA算法包括BRISQUE[24],NIQE[25],IL-NIQE[26],FISBLIM[5],SISBLIM[6].为了方便观看,表2中用黑体字表示性能最高的一个算法.
从表2中可以看出:1)本文提出的算法在MLIVE数据库和MDID2013数据库上都具有很好的主客观一致性和很高的准确性,与其它算法相比性能最优,能够满足混合失真图像质量评价的需求;2)在所有FR-IQA算法中VIF算法性能最优,VIF算法通过探索图像信息量与视觉质量之间的关系,计算失真图像相对于无失真参考图像信息丢失的程度,评价失真图像的质量,取得了较好的性能.但在很多实际应用场合下,我们无法得到原始参考图像的任何信息,FR-IQA算法的应用有着明显的局限性;3)所有算法在MLIVE数据库上的性能都优于在MDID2013数据库上的性能,因为MLIVE数据库图片只是2种失真类型的混合,而MDID2013数据库图片是3种失真类型的混合,失真形式更复杂,给客观图像质量评价算法带来更多的困难和挑战.

表2 算法性能比较Tab.2 Performance comparison of algorithms
从性能比较中可以看出,本文提出的算法在图像质量评价中获得了非常好的性能.因为图像经DCT变换和量化后高频成份衰减,损失了图像的部分细节信息,应用DCT变换和量化原理的JPEG失真图像在沃尔什哈达玛变换域投影得到的局部沃尔什哈达玛变换图会相应地出现模糊和块失真,图像边缘不均匀扩展;图像经WN失真后,出现噪声点,高频成份增加,WN失真图像在沃尔什哈达玛变换域投影得到的局部沃尔什哈达玛变换图高频成份相应地增加;图像经Gblur失真后,图像模糊,高频成份衰减,部分细节信息丢失,Gblur失真图像在沃尔什哈达玛变换域投影得到的局部沃尔什哈达玛变换图高频成份相应地丢失,出现模糊效应,图像边缘扩展,且边缘扩展均匀.尽管JPEG,WN,Gblur这3种失真类型的失真原理不同,但是都引起了图像低频、高频成份的相应变化.因此,通过分析低频、高频成份的统计特性能够很好地反映图像的失真情况.MLIVE数据库和MDID2013数据库图片是JPEG,WN和Gblur这3种失真的不同组合,组合失真对图像的低频成份和高频成份产生的影响不同,在沃尔什哈达玛变换域的表现方式不同,变换域的局部沃尔什哈达玛变换图的统计特性自然也不同.局部沃尔什哈达玛变换图的零列率项和非零列率项分别对应图像的低频成份和高频成份,本文通过分析零列率项和非零列率项的旋转不变LBP统计特征表征图像的失真程度.与前人算法不同的是,本算法不需要关于图像失真类型的先验信息,仅仅通过分析图像低频成份和高频成份的统计信息,实现了混合失真图像的质量评价,因此其更具备优势,同时实验结果也表明本文提出的算法可以很好地区分不同程度的失真,得到了很好的性能.
4.4 参数影响分析
LWHT的阶数和图像的尺度影响算法的性能,本文分别探究了LWHT阶数(以三尺度为例)和多尺度(以四阶WHT为例)对算法性能的影响.实验结果见表3和表4.
综合分析表3和表4,本算法在选取不同阶和不同尺度情况下都具备优越的实验性能.从表3中可以发现,算法采用四阶和八阶WHT(以三尺度为例)时性能较好;从表4中可以发现,算法采用三尺度(以四阶WHT为例)时性能最好,所以本文综合考虑,算法采用了四阶WHT和三尺度进行的图像特征提取.

表3 不同阶算法性能比较Tab.3 Performance comparison of different order algorithms
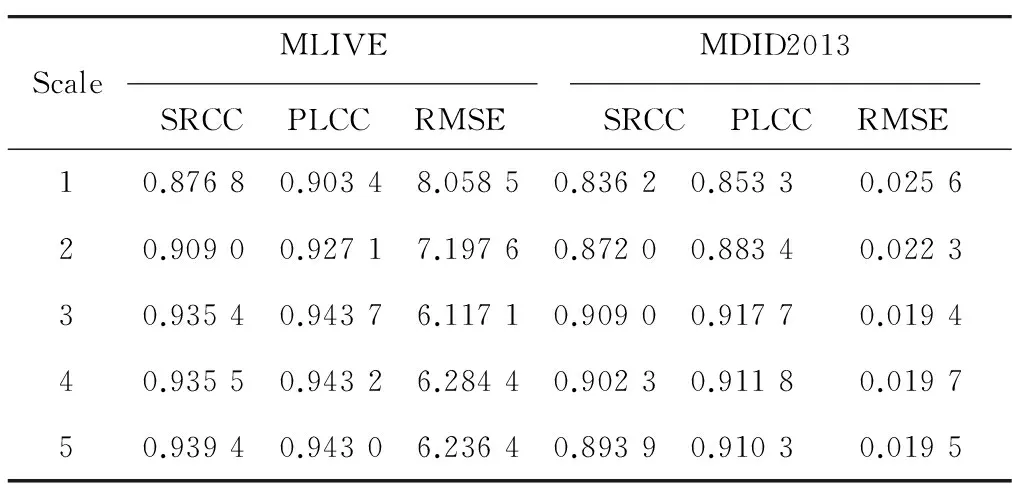
表4 不同尺度算法性能比较Tab.4 Performance comparison of different scale algorithms
5 结 论
本文提出了一种针对混合失真类型的无参考图像质量评价方法.通过利用图像在3个WHTK上的投影,得到局部沃尔什哈达玛变换图,同时采用多尺度的方法在局部沃尔什哈达玛变换图上进行图像的特征提取.将特征输入到SVR网络进行训练,得到训练模型,实现特征到质量分数的映射.本文提出的算法具有很好的主客观评价一致性,性能优于现有较优秀的FR-IQA算法和NR-IQA算法.未来进一步拓展本算法至视频领域,以满足视频质量评价的需求;同时,应用本算法对传输系统的图像质量评价也将有助于传输系统的优化.
[1] WU H R,REIBMAN A R,LIN W,etal.Perceptual visual signal compression and transmission[J].Proceedings of the IEEE,2013,101(9):2025-2043.
[2] GU K,ZHAI G,LIN W,etal.The analysis of image contrast:from quality assessment to automatic enhancement[J].IEEE Transactions on Cybernetics,2016,46(1):284-297.
[3] WANG Z,BOVIK A C,SHEIKH H R,etal.Image quality assessment:from error visibility to structural similarity[J].IEEE Transactions on Image Processing,2004,13(4):600-612.
[4] LI L,LIN W,WANG X,etal.No-reference image blur assessment based on discrete orthogonal moments[J].IEEE Transactions on Cybernetics,2016,46(1):39-50.
[5] GU K,ZHAI G,LIU M,etal.FISBLIM:a fIve-step BLInd metric for quality assessment of multiply distorted images[C]//SiPS 2013 Proceedings.Taipei City,2013:241-246.
[6] GU K,ZHAI G,YANG X,etal.Hybrid no-reference quality metric for singly and multiply distorted images[J].IEEE Transactions on Broadcasting,2014,60(3):555-567.
[7] LI C,ZHANG Y,WU X,etal.Blind multiply distorted image quality assessment using relevant perceptual features[C]//Image Processing (ICIP),2015 IEEE International Conference on.Quebec City,QC,2015:4883-4886.
[8] LU Y,XIE F,LIU T,etal.No reference quality assessment for multiply-distorted images based on an improved bag-of-words model[J].IEEE Signal Processing Letters,2015,22(10):1811-1815.
[9] CHANDLER D M.Seven challenges in image quality assessment:past,present,and future research[J].Isrn Signal Processing,2014,2013(8):1-53.
[10]李树涛,孙凤梅.基于Curvelet和小波变换的纹理图像识别[J].湖南大学学报:自然科学版,2008,35(4):51-54.
LI Shutao,SUN Fengmei.Texture recognition based on curvelet and wavelet transformation[J].Journal of Hunan University:Natural Sciences,2008,35(4):51-54.(In Chinese).
[11]周四望,罗孟儒.顺序小波包图像压缩感知方法[J].湖南大学学报:自然科学版,2015,42(4):130-135.
ZHOU Siwang,LUO Mengru.Sequential image compressed sensing based on wavelet packet[J].Journal of Hunan University:Natural Sciences,2015,42(4):130-135.(In Chinese).
[12]LAKSHMI P G,DOMNIC S.Walsh-Hadamard transform kernel-based feature vector for shot boundary detection[J].IEEE Transactions on Image Processing,2014,23(12):5187-5197.
[13]UZUN-PER M,GOKMEN M.Face recognition with a novel image representation:local walsh-hadamard transform[C]//Visual Information Processing (EUVIP),2014 5th European Workshop on.Paris,2014:1-6.
[14]MENG J,GAO Y,WANG X,etal.Face recognition based on local binary patterns with threshold[C]//Granular Computing (GrC),2010 IEEE International Conference on.San Jose,CA,2010:352-356.
[15]ZHANG M,XIE J,ZHOU X,etal.No reference image quality assessment based on local binary pattern statistics[C]//Visual Communications and Image Processing (VCIP).Kuching,2013:1-6.
[16]SALOMON D.Data compression:the complete reference [M].4th ed.New York,USA:Springer-Verlag,2007:289-294.
[17]SAAD M A,BOVIK A C,CHARRIER C.Blind image quality assessment:a natural scene statistics approach in the DCT domain[J].IEEE Transactions on Image Processing,2012,21(8):3339-3352.
[18]JAYARAMAN D,MITTAL A,MOORTHY A K,etal.Objective quality assessment of multiply distorted images[C]//2012 Conference Record of the Forty Sixth Asilomar Conference on Signals,Systems and Computers (ASILOMAR).Pacific Grove,CA,2012:1693-1697.
[19]SHEIKH H R,SABIR M F,BOVIK A C.A statistical evaluation of recent full reference image quality assessment algorithms[J].IEEE Transactions on Image Processing,2006,15(11):3440-3451.
[20]CHANDLER D M,HEMAMI S S.VSNR:a wavelet-based visual signal-to-noise ratio for natural images[J].IEEE Transactions on Image Processing,2007,16(9):2284-2298.
[21]SHEIKH H R,BOVIK A C.Image information and visual quality[J].IEEE Transactions on Image Processing,2006,15(2):430-444.
[22]ZHANG L,ZHANG L,MOU X,etal.FSIM:a feature similarity index for image quality assessment[J].IEEE Transactions on Image Processing,2011,20(8):2378-2386.
[23]XUE W,ZHANG L,MOU X,etal.Gradient magnitude similarity deviation:a highly efficient perceptual image quality index[J].IEEE Transactions on Image Processing,2014,23(2):684-695.
[24]MITTAL A,MOORTHY A K,BOVIK A C.No-reference image quality assessment in the spatial domain[J].IEEE Transactions on Image Processing,2012,21(12):4695-4708.
[25]MITTAL A,SOUNDARARAJAN R,BOVIK A C.Making a “Completely Blind” image quality analyzer[J].IEEE Signal Processing Letters,2013,20(3):209-212.
[26]ZHANG L,ZHANG L,BOVIK A C.A feature-enriched completely blind image quality evaluator[J].IEEE Transactions on Image Processing,2015,24(8):2579-2591.
No-reference Image Quality Assessment on Walsh Hadamard Transform Domain
HOU Chunping,LIU Yue,YUE Guanghui†,FENG Dandan,MA Tongtong
(School of Electrical and Information Engineering,Tianjin University,Tianjin 300072,China)
Generally speaking,distortion will change the statistical characteristics of low frequency and high frequency components of images.With this consideration,a novel no-reference image quality assessment algorithm was proposed to the predict the perceived quality of multiply-distorted images.First,the images were transformed into local Walsh Hadamard Transform maps by local Walsh Hadamard Transform.Then,the features (i.e.,rotation invariant local binary pattern features of zero sequency term and non-zero sequency term) were extracted on local Walsh Hadamard Transform maps to reflect low frequency and high frequency components of images.Finally,the extracted features were trained using support vector regression to form the model,which implemented mapping from the feature space to the quality scores.Comprehensive evaluations were conducted on two multiply-distorted databases (MLIVE database and MDID2013 database),and experimental results show that the proposed method consists well with human subjective perception.Besides,the performance of algorithm is statistically superior to the existence of better full-reference image quality assessment and non-reference image quality assessment algorithms.
image quality assessment (IQA);no-reference (NR);local Walsh Hadamard Transform (LWHT);local binary pattern (LBP);support vector regression (SVR)
1674-2474(2017)08-0137-08
10.16339/j.cnki.hdxbzkb.2017.08.021
2016-09-18
重点国际(地区)合作研究资助项目(61520106002),International (Regional) Cooperation and Exchange Program(61520106002);国家自然科学基金资助项目(61471262),National Natural Science Foundation of China(61471262);教育部博士点基金资助项目(20130032110010),Doctoral Fund of Ministry of Education of China(20130032110010)
侯春萍(1957-),女,天津人,天津大学博士生导师,教授
†通讯联系人,E-mail:yueguanghui@tju.edu.cn
TP391
A

