块转换网络和分级超立方体网络的化学指标计算

高 炜，梁 立

（云南师范大学 信息学院，云南 昆明 650500）

块转换网络和分级超立方体网络的化学指标计算

高 炜，梁 立

（云南师范大学 信息学院，云南 昆明 650500）

在理论化学中，通过特定分子结构的指标计算可以分析该化合物的化学、药学和生物学性质，为其工程应用提供参考。通过化学图结构的具体分析，对其边的类型进行划分，再通过指数的定义给出块转换网络和分级超立方体网络的基于度的化学指标。

理论化学；分子图；分级超立方体网络；拓扑指数

化学图论作为图论和化学的交叉学科，已成为理论化学的研究重点，受到化学、数学、制药学、医学和材料科学等诸多领域研究者的关注。在化学图论中，对每个分子结构进行图表示，用顶点来表示原子，用边来表示连接原子的化学键。由此类方法构造的图称为分子图。大量的化学研究已经证明化合物的化学、药学和生物特性与它们的分子结构有着潜在的联系。从而可以通过对定义在化学图上的化学指标进行计算来研究化合物的特性，这一方法得到很多研究者的欢迎并由此成为研究的热点[1-10]。设G是一个分子图，其原子集合（顶点集）和化学键集合（边集）分别用V（G）和E（G）表示。笔者研究的分子图均为简单图，文中关于图的术语若没有特别说明则与文献[11]一致。

以下设e=uv是分子图G的一个化学键（边），对任意u∈V（G），d（u）表示顶点u在分子图中的度。下面列出的是几种重要的指数或多项式。

其中 t1和 t2为任意非负整数，mij（G）=|{e=uv|d（u）=i，d（v）=j}|，λ＜0 为实数，k 是任意实数。

笔者主要研究块转换网络和分级超立方体网络的若干基于度的化学指数，并给出它们的精确表达式。

1 主要结果及证明

1.1 块转换网络

块转换网络（BSN-1）n×n和（BSN-2）n×n是一种重要的分级互连网络，其结构如图 1和图 2所示。

图1 3×3块转移网络

图2 块转移网络（BSN-2）1×1

对于（BSN-1）n×n而言，通过其结构分析可知其边集合可以划分以下两类：

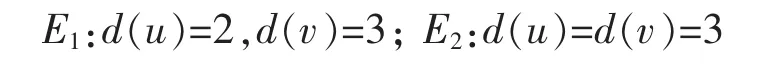
并通过计算可知｜E1|=8，｜E2|=24n2-10。由指数的定义，进一步可得

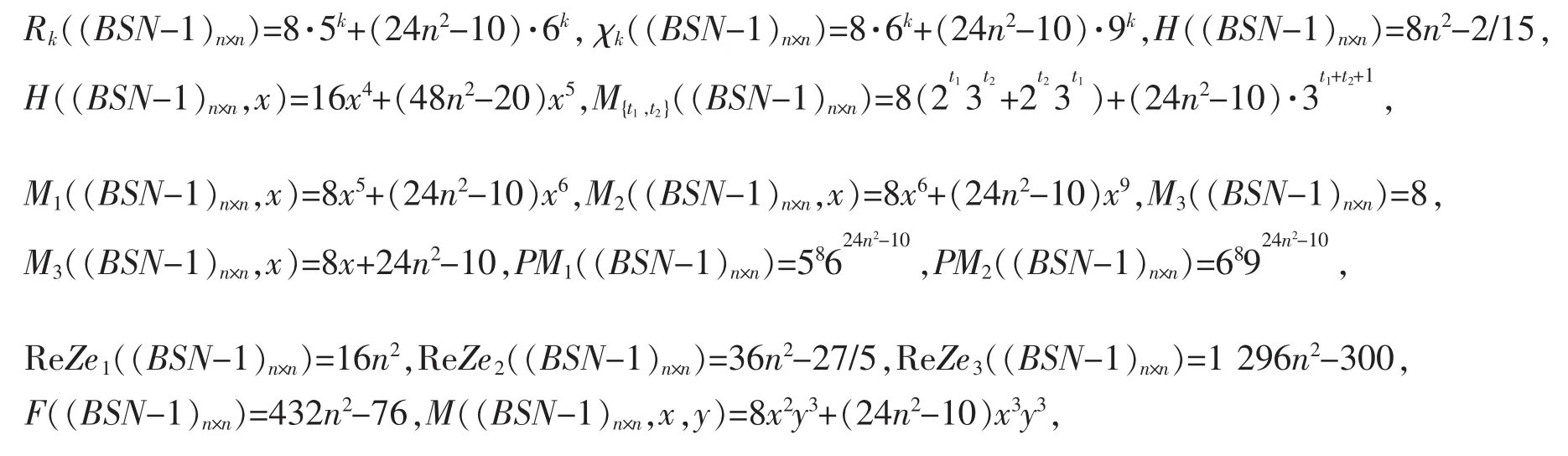
对于（BSN－2）n×n而言，通过其结构分析可知其边集合可以划分以下两类：

并通过计算可知｜E1｜＝12，｜E2｜＝32n2-14。 由指数的定义，进一步可得

1.2 分级超立方体网络

下面将给出两类分级超立方体网络 （HHC－1）n×n和（HHC－2）n×n的一些重要化学指标，其分子图结构可参考图3。

对于（HHC－1）n×n而言，通过其结构分析可知其边集合可以划分以下两类：

并通过计算可知｜E1｜＝16，｜E2｜＝24n+4。 由指数的定义，进一步可得

图3 两类分级超立方体网络分子图结构

对于（HHC－2）n×n而言，通过其结构分析可知其边集合可以划分以下两类：

并通过计算可知｜E1｜＝24，｜E2｜＝32n+4。 由指数的定义，进一步可得

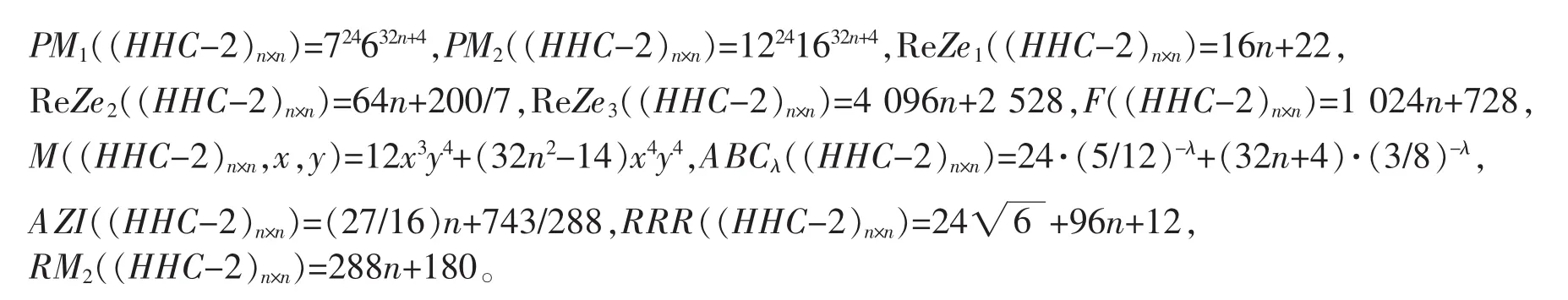
2 结语

通过研究块转换网络和分级超立方体网络的结构特征，得到它们的若干基于度的化学指数的精确表达式。块转换网络和分级超立方体网络是化学分子中广泛出现的基本结构，对这两类结构的研究有助于了解包含这两类结构的一些化合物的化学、药学和材料学特征。从这一角度来说，文中得到的结果在工程领域具有一定的潜在应用价值。

[1]GAO W，WANG W F.Revised szeged index and revised edge-szeged index of special chemical molecular structures[J].Journal of Interdisciplinary Mathematics，2016，19（3）：495-516.

[2]高炜，贾志洋.特殊纳米管的顶点带权维纳数[J].黑龙江大学学报（自然科学版），2016，33（3）：308-314.

[3]宴立，高炜.关于哈拉里指数和多重维纳指数的注记[J].云南师范大学学报（自然科学版），2016，36（2）：38-41.

[4]彭波，高炜.几类分子结构的基于度的指数[J].数学理论与应用，2016，36（1）：81-87.

[5]高炜，梁立.给定参数下图的广义哈拉里指数[J].新乡学院学报，2016，33（33）：1-3.

[6]GAO W，SIDDIQUI M K，IMRAN M，et al.Forgotten topological index of chemical structure in drugs[J].Saudi Pharmaceutical Journal，2016，24：258-264.

[7]GAO W，FARAHANI M R，SHI L.Forgotten topological index of some drug structures[J].Acta Medica Mediterranea，2016，32：579-585.

[8]GAO W，SHI L，FARAHANI M R.Distance-based indices for some families of dendrimer nanostars[J].IAENG International Journal of Applied Mathematics，2016，46（2）：168-186.

[9]GAO W，WANG W F.The eccentric connectivity polynomial of two classes of nanotubes[J].Chaos，Solitons and Fractals，2016，89：290-294.

[10]GAO W，FARAHANI M R，JAMIL M K.The eccentricity version of atom-bond connectivity index of linear polycene parallelogram benzenoid ABC5（P（n，n））[J].Acta Chimica Slovenica，2016，63：376-379.

[11]BONDY J A，MUTRY U S R.Graph Theory[M].Berlin：Springer，2008：1-40.

Chemical index computation of block shift network and hierarchical hypercube network

GAO Wei，LIANG Li
（School of Information，Yunnan Normal University，Kunming 650500，China）

In theoretical chemistry,the index calculated by the specific molecular structure can be used to analyze the chemical，pharmaceutical and biological properties of the compound,and provide a reference for its engineering application.We analyzed the chemical graph structures in detail and classified the edge types.Then we gave the degree-based chemical indicators of block shift network and hierarchical hypercube network by their index definitions.

theoretical chemistry；molecular graph；hierarchical hypercube network；topological index

O157.6 MR（2010）Subject Classification：05C76；05C90

A

2096－3289（2017）03－0037－04

责任编辑：谢金春

2016－07－29

国家自然科学青年基金资助项目（11401519）

高 炜（1981-），男，浙江绍兴人，副教授，博士，研究方向：图论、统计学习理论和智能计算。