基于向量自回归模型的中美股市联动性分析

莫悠+程锐

摘要：文章选取中国的上证综合指数和美国标准普尔500指数在2015年1月2日至2016年12月31日的数据作为研究样本，利用向量自回归（VAR）模型的Johansen协整检验和Granger因果检验方法，对中国股市和美国股市的联动性进行了实证研究分析。结果显示，中美两国股市具有长期均衡的正相关关系。

关键词：向量自回归模型；中美股市；联动性

一、引言

证券市场是金融市场的重要组成之一，证券市场的波动常常是国民经济的晴雨表。QFII的引入机构投资者能够进入国际市场，使得国内外投资交流日益密切，投资者的投资策略也在与时俱进，全球范围内的资产组合配置不断增多，各国的股市联动性增强。另一方面全球经济一体化背景下，各国经济波动的紧密相连，这种波动也会一定程度上反映在全球的股市联动上。本文首先从理论上对全球股票市场联动作用机制进行了阐述。然后从实证的角度，具体的对中美两国间股市联动性进行了研究。

二、文献综述

（一）国内外研究现状

近年来关于我国股票市场联动性已有部分学者进行了研究。张福、赵华等（2004）对中国股市和美国股市联动性进行了分析，发现在QFII的引入前后，两者关联性有明显的区别，在B股市场向境内投资者开放前，两国股市在收益率和波动性上没有显著的关联，而在开放后中国股票市场和美国股票市场股价走势在统计上趋同，存在长期的均衡关系。Robert A.Connolly和F.Albert Wang（2003）以各国公布宏观经济消息为参考标准，通过实证分析美、英、日三国证券市场的联动性，研究发现很多波动的产生不能完全从宏观经济消息上找到原因，而国美外市场的联动影响是回报率产生波动的主要影响因素。张学功，薛志，超吕龙（2016）用SV-t模型和PairCopula分解模型对中国、日本和美国三国的股市相关性进行研究，结果表明美国和日本两国间的股市相关性最强。中国和日本的股市相关性强于中国和美国的股市相关性。龚金国，史代敏（2015）进一步探究了中美股市变动的原因，发现中美股市存在联动，但中国金融自由并不是联动的主要原因，贸易自由化在股市联动中起到了很大的作用。

（二）文献评述

在文献阅读中我们发现，首先不同的学者在研究股市长期相关性时会产生不同的结果，这是因为作者没有详细介绍其模型选取的标准，选取的模型不同，结果可能大相径庭。很多研究都是基于某一事件对两国股市的分析，这种方式得出的结果稳健性欠缺。最后，大部分文章所得到的结论值得商榷，没有仔细的探索联动性的形成机制，不够严谨。

三、理论基础

关于全球股票市场联动的作用机制，主要有经济基础假说和市场传染假说。经济基础假属于传统金融理论，认为所有投资者都是完全理性的，是由各国资产基本面的联系从而引起了股价间的联动。Contessi et al（2010）和Gerrits&Yuce（1999）的研究也支持了经济基础假说。市场传染假说认为股市联动性不能完全由得宏观经济联系解释，而更应该从投资者行为上寻找原因。可以看出此假说更偏向于对个体行为的研究，把重点放在投资者行为或者金融市场所特有的行为特征上。King&Wadhwani（1990）、Connolly&Wang（2002），Robert A.Connolly和F.Albert Wang（2003）等实证研究结果都支持了市场传染假说。

本文认为这两种假说是殊途同归的，股票市场的波动受多方面因素的影响。一方面股价是国家经济的一个前瞻性指标，随着国际间分工合作的加强，越来越多国家间有共同的经济基础，那么共同的经济波动也必然会反应到各国的股市上，而股市的波动正是一个各国经济信号释放的过程。另一方面当一国股市动荡时，由于投资全球化的影响，必然会传染到其他国家，产生联动反应。由此分析可以看出，在全球股市波动中，市场感染和经济基础假说是对立统一的。

四、数据

（一）样本数据选取

选取上证综合指数（SZ）和标準普尔 500 指数（BP）和为样本进行研究，中国股票市场的考察对象为上证综合指数（SZ），此指数是当下学者们研究此问题时较常使用的，它能较为充分地反映我国每日股市大盘的总体行情。美国股票市场以标准普尔 500 指数（BP）为研究样本，该指数包美国市场上90%以上的成份股，能较为充分的代表美国市场。

（二）数据处理方法

本文收集了Wind数据库中从2015年1月2日到2016年12月31日上证指数和美国标准普尔500指数每日的收盘点位，共得到473组数据。数据处理说明，1.同一交易日，不考虑时差的影响，由于两国存在时差中国股市与美国股市从开盘到收盘的交易时间相差七个半小时。中美两国股市的开盘和收盘时间之间没有重叠的部分，但为研究的方便，本文文中我们不考虑这种时差的影响。2.由于两国习俗假日的差异导致交易日也会有所不同，本文删除了两个市场交易日不重叠的部分使数据匹配度更好。

五、实证分析

（一）数据描述

本文以上证综合指数和标准普尔500指数2015年1月2日到2016年12月31日的日数据为研究对象，采用Eviews7.0软件进行统计分析。数据描述如表1所示。

（二）时间序列的平稳性检验

由图1可知，上证综合指数（SZ）与标准普尔500指数（BP）都是非平稳时间序列，利用Eviews7.0采用ADF检验方法进一步检验数据的平稳性，所得结果如表2所示。endprint

两者的单位根检验的结果表明，上证综合指数（SZ）的ADF值为-1.5，ADF值大于各个显著性水平下的临界值，所以拒绝原假设，即上证综合指数（SZ）是非平稳的，含有单位根。进一步对上证综合指数（SZ）的一阶差分（DSZ）进行检验，ADF的统计值小于各个显著性水平下的临界值，说明差分后的序列是平稳的。因此SZ是一阶单整，即I（1）。同理运用ADF的方法对标准普尔500指数（BP）和其一阶差分（DBP）进行检验，上证综合指数（SZ）的ADF值大于各个显著性水平下的临界值，标准普尔500指数（BP）的一阶差分的ADF值也大于各个显著性水平下的临界值，同理可表明BP也是一阶单整，即I（1）。

（三）协整关系检验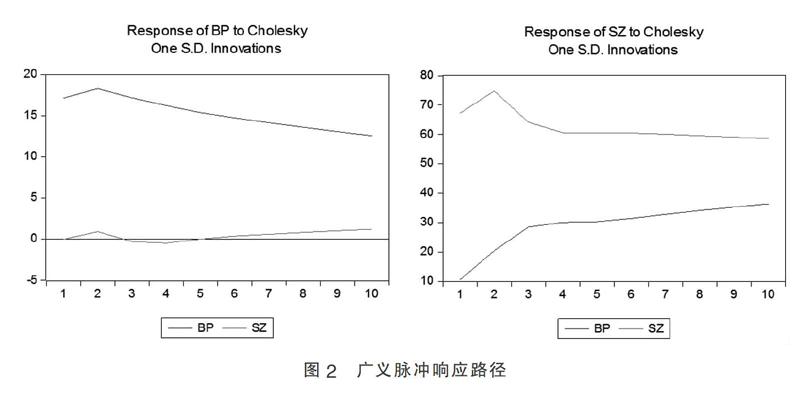

上面的单位根检验证明了两指数的非平稳的，下面继续用协整关系检验中的Engle-Granger检验法检验两非平稳变量之间的长期均衡关系。利用Engle-Granger检验法首先对两变量序列进行OLS回归，得到残差序列。然后对残差序列进行ADF检验，若残差序列平稳，则表示这两个变量序列存在协整关系。利用Eviews7.0对上证综指（SZ）和美国标准普尔500（BP）指数进行OLS回归，并对其残差序列进行ADF检验，结果如表3所示。

这表明在2015年1月1日到2016年12月31日期间上证综合指数（SZ）和标准普尔500指数（BP）存在长期的稳定关系。为确定从而初步确定它们之间是否存在联动性，我们在通过协整检验后，下面对变量进一步的进行格兰杰因果关系检验。

（四）格兰杰因果关系检验

通过前面的协整关系检验已经得出了上证综指数（SZ）和美国标准普尔500（BP）之间存在着长期稳定的均衡关系的结论。但对于两者间相互影响的的前后关系即到底是中国股市影响了美国股市还是美国股市影响了中国股市，我们将通过下面的通过格兰杰因果关系检验进行验证。我们对上证综合指数（SZ）和美国标准普尔500（BP）进行格兰杰关系检验，得出的结果如表4所示。

由表4我们可以看到，在10%的显著水平上，当滞后期为2、4、5时，接受“SZ不是BP的格兰杰原因”的原假设。即上证综合指数不是标准普尔500指数变化的格兰杰原因。同时拒绝“BP不是SZ的格兰杰原因”的原假设，即标准普尔500指数是上证综合指数变化的原因。而当滞后期为3时则相反。因此，我们可以发现上证综合指数（SZ）和标准普尔500指数（BP）之前存在着一定的联动性。还可以进一步发现，标准普尔500指数（BP）对上证综合指数（SZ）变化的影响更为显著。

（五） 基于VECM的脉冲响应分析

为了来描述变量间的对单位冲击的动态反应，我们引进向量误差修正模型（VECM）来判断变量之间存在的互动关系及持续性。在向量误差修正模型（VECM基础上用脉冲响应分析能够直观的揭示出中国和美国股市之间的动态变化。图2描述了上证综合指数（SZ）与标准普尔500指数（BP）的广义脉冲响应路径。

从图2中单位正冲击的强度来看，中美两国股市不是相互独立的而是相互关联的，而且在两国的相互影响的关系中，美国股市对中国股市的冲击更大，美国股市一单位正冲击对中国股市的影响强度超过了中国股市一单位正冲击对美国股市的影响强度。这也进一步证实了格兰杰因果检验的的结果，相比于中国股市，美国股市在两国股市波动中有着引导作用。

六、结语

本文对中国股市收益率和美国股市收益率的联动性的进行了实证分析，通过以上实证研究可以下结论，首先，在本文所研究的中样本期中，中国股市和美国股市两者的整体走势是相互一致的，是存在长期均衡关系的。对于这个结论我们也很容易理解，因为随着全球经济一体化，全球市场分工合作的不断加强，各国股市间的联系也必然越来越紧密，中美作为世界上两大重要经济体，两国间相互合作越来越多元化，这也必然导致了两国股市的紧密相关。其次，文中两只股指之间经检验是存在双向的格兰杰因果关系的。中美两国间股市存在的长期均衡关系是稳固的，说明美国与中国在经济上是密切联系的。最后，在动态相关性方面，我们发现中美股市之间有显著相关的，但相关程度并不很高，且正相关关系占大多数。

综上我们发现国与国之间股市联动性越来越强。对于投资者和投资机构来说，需要更加谨慎我们的投资行为。试图通过国家投资来分散投资风险可能越来越不能奏效，国际股市股市联动性的加强使得想通过国际分散投资的获取收益空间的机会越来越少。此外，准确的预测股市走势十分重要，利用计量模型来指导投资策略，例如可根据跟本文中联动性研究的实证结果，有效规避市场波动带来的风险。例如利用先波动的指数方向来指导后波动指数的投资，从而获得理想的投资收益。

参考文献：

[1]张福，赵华，赵媛媛.中美股市协整关系的实证分析[J].统计与决策，2004（02）.

[2]潘文荣，刘纪显.QFII及QDII制度引入后的中美股市聯动性研究[J].江西财经大学学报，2010（01）.

[3]宋玉臣，乔木子.中美股票市场信息冲击的非对称性调整特征与联动性效应——基于门限协整的误差修正模型[J].浙江社会科学，2016（09）.

[4]杨雪莱，张宏志.金融危机、宏观经济因素与中美股市联动[J].世界经济研究，2012（08）.

[5]王建新，许婷婷.中美股市的联动分析[J].对外经贸，2012（06）.

[6]张学功，薛志超，吕龙.基于Pair Copula-SV-t模型的金融市场相关性分析[J].金融与经济，2016（04）.

[7]刘悦莹.后危机时期中美股市的联动性分析[J].佳木斯大学学报（自然科学版），2015（05）.

（作者单位：贵州大学）endprint