基于PSO-BP神经网络光电编码器误差补偿研究*

陈洪月,张 坤,刘治翔,王 鑫

(辽宁工程技术大学机械工程学院,辽宁 阜新 123000)

基于PSO-BP神经网络光电编码器误差补偿研究*

陈洪月*,张 坤,刘治翔,王 鑫

(辽宁工程技术大学机械工程学院,辽宁 阜新 123000)

考虑到高精度绝对式光电编码器应用广泛,其角度测量精度对整个系统精度影响较大,但由于角度传感器生产安装过程中产生的误差等原因,使得传感器在实际应用中存在一定的误差。而使用传统误差补偿方法难以得到较好的补偿效果,本文使用一种基于PSO的BP神经网络作为角度传感器误差补偿系统的算法。通过实验验证,该种算法能够对角度传感器误差进行较好的补偿,与补偿前相比,其标准偏差提高了12.5倍,最大误差和平均误差降低到9.6%和8.5%,提高了传感器检测精度。与使用了基于传统BP神经网络和基于多项式拟合算法的误差补偿系统进行对比实验,结果表明,其补偿效果亦优于这两种算法。

绝对式光电编码器;BP神经网络;粒子群优化算法;误差补偿;角度传感器

绝对式光电编码器是一种角度测量仪器,其能够将输出轴的机械模拟量通过光电转换原理转换为脉冲信号或者数值信号,从而对角度进行测量。绝对式光电编码器因其具有精度高、尺寸小、可靠度高等优势而在工业加工、航天、机器人等领域得到广泛应用。随着科学技术的不断进步,在航天科技、机器人、高精度测试等领域对系统的精度要求亦不断增加,这就需要绝对式光电编码器具有更高要求的分辨率以及测量精度等性能来满足系统的要求。但是由于绝对式光电编码器细分误差、码盘偏心以及监测误差等原因造成了绝对式光电编码器误差的产生。因此有必要对绝对式光电编码器误差进行补偿以提供传感器的测量精度[1-3]。

1 传感器测量误差来源及表示

本文研究的角度传感器为16位绝对式光电编码器,传感器的误差来源主要有:传感器在进行装配调试时的偏心误差、轴系误差以及传感器在进行生产制造时的码盘误差。传感器误差由标准偏差σ、误差最大值emax以及误差平均值emean来表示。

标准偏差σ可以表示为:

(1)

式中:n表示对传感器的测试点点数;ei表示传感器在第i个测量点上的误差,具体表达式为:

ei=θi,T-θi,L, i=1,2,3,…,n

(2)

传感器误差最大值emax可以表示为:

emax=max|θi,T-θi,L|, i=1,2,3,…,n

(3)

传感器误差平均值emean可以表示为[4-6]:

(4)

2 传感器误差补偿方法及其优化

2.1 BP神经网络

BP神经网络通常由输入层、输出层和隐含层组成。BP神经网络的输出和实际类型yk的误差之和表示:

(5)

式中:Ek表示为:

(6)

隐含层中第i个输出公式为:

(7)

BP神经网络调整权值公式:

(8)

(9)

第r层的神经网络权值调整公式:

(10)

BP神经网络实际上是梯度下降算法的一种迭代学习方法。由于梯度下降算法要求具有较小的学习速度时才能进行稳定的学习,因此这种方法的收敛速度较慢。并且,由于BP神经网络在进行训练时,会在某点沿着误差斜面而渐进误差极值,因此不同的起点会得到不同的误差极值和不同的解。因此传统BP神经网络具有学习速度慢、抗干扰能力弱以及容易陷入局部最小值等缺点。

2.2 粒子群优化算法

粒子群优化算法PSO是一种使用实数求解的,易于实现的基于群体智能的全局搜索算法。在迭代过程中,每个粒子通过不断追逐个体极值pbest和全局极值gbest来更新自身位置:

(11)

(12)

2.3 基于PSO的BP神经网络优化

BP神经网络中样本输出值与实际输出值误差平方和最小是BP神经网络训练的目标,即粒子群优化算法中适应值达到最大,文献[7]中提出一种基于PSO的BP神经网络优化方法,将适应值函数设定为:

(13)

式中:M为学习样本个数;d(t)为样本的输出;p(t)为实际输出。

粒子群优化算法需要对连接权值进行优化的个数为:

M=m×(n+1)+m+1

(14)

式中:n为输入层神经元个数;m为隐含层神经元个数。

将BP神经网络原始的初始权值和阈值由通过粒子群优化算法优化后的初始权值和阈值代替,构建基于PSO的BP神经网络训练模型,以消除BP神经网络训练速度慢,容易陷入局部最小值等缺点[7]。

3 传感器误差补偿实验

3.1 传感器误差补偿实验装置

本文采用项目组自主研制的角度传感器检测装置对传感器测量精度及误差补偿进行实验,该装置可对分辨率低于18位的角度传感器进行精度检测实验。角度传感器检测装置工作原理如图1所示。

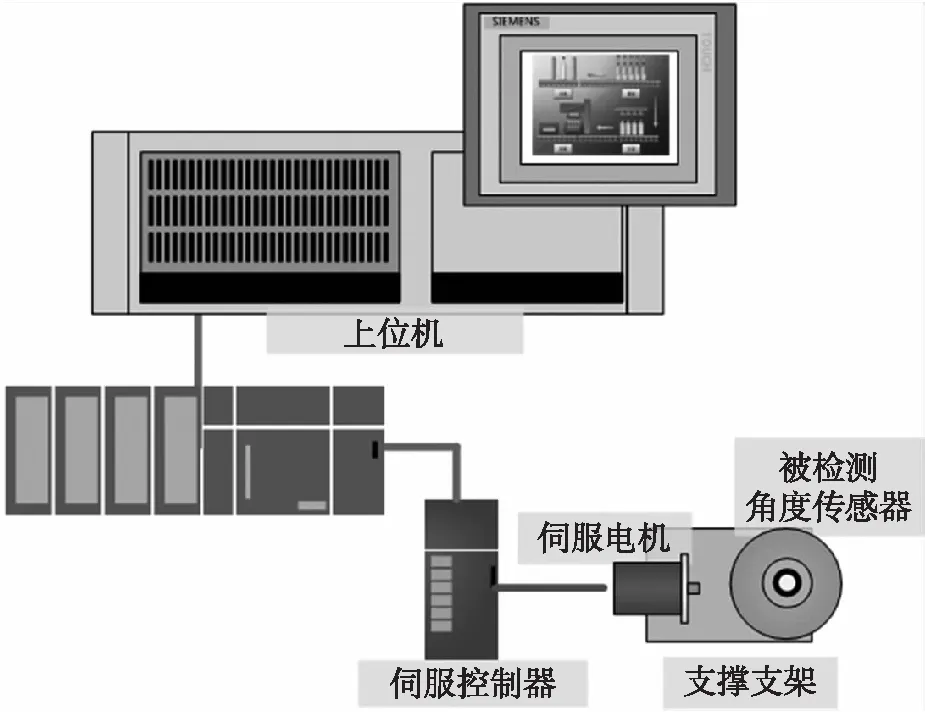
图1 角度传感器检测装置原理框图

角度传感器检测装置主要由高精度伺服电机、伺服电机驱动器、可编程控制器、上位机计算机以及支撑支架等组成。上位机计算机与可编程控制器通过485总线通信,设定对传感器的检测次数和测量点数等。可编程控制器接收上位机下达的采集指令后,完成对角度传感器的控制和检测任务,首先通过向伺服电机驱动器下达转动一个微小角度的脉冲信号,伺服电机驱动器接到脉冲信号后控制高精度伺服电机转动一个微小角度,认为该角度是真实角度。被检测角度传感器将检测到的微小角度值反馈至可编程控制器的数据采集模块中,经过运算得到被检测角度传感器检测到的角度,通过差值运算即得到被检测角度传感器的检测误差,最后可编程控制器将检测误差上传至上位机计算机储存,用于研究传感器的误差补偿[8]。

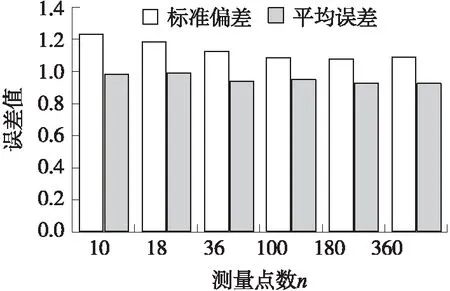
图2 传感器重复测量之间的平均误差以及标准偏差

3.2 误差补偿实验及数据处理

使用角度传感器检测装置对工业中应用较多的J3806型绝对式光电编码器进行精度实验研究。设定n为编码器旋转一周,检测装置的测量点数,将n分别设定为10、18、36、100、180、360,通过多次分别测量,得到了传感器在对应测量点上传感器重复测量之间的平均误差以及标准偏差如图2所示。

从实验数据可以看出,在进行多次测量过程中,角度传感器检测装置具有较好的测量重复性,在对应测量点上,多次重复测量之间的平均误差之差仅为0.05°。通过对传感器标准偏差的观察可以看出,当测量点数n在较小范围内时,随着测量点数n的增加,传感器标准偏差会随之减小,但是当测量点数n在较大范围内时,随着测量点数n的增加,传感器标准偏差没有明显变化,而随着测量点数n的增加,大大增加了实验的复杂程度、数据处理工作量以及处理时间,而且不利于传感器的精度的测量,一般将测量点数n设定在10～36这个范围内[9]。

本文在进行角度传感器检测时,将测量点数n设定为36,得到了传感器精度检测实验数据,其中一次数据如表1所示。两次检测实验的误差对比如图3所示。

图3 传感器精度检测误差对比

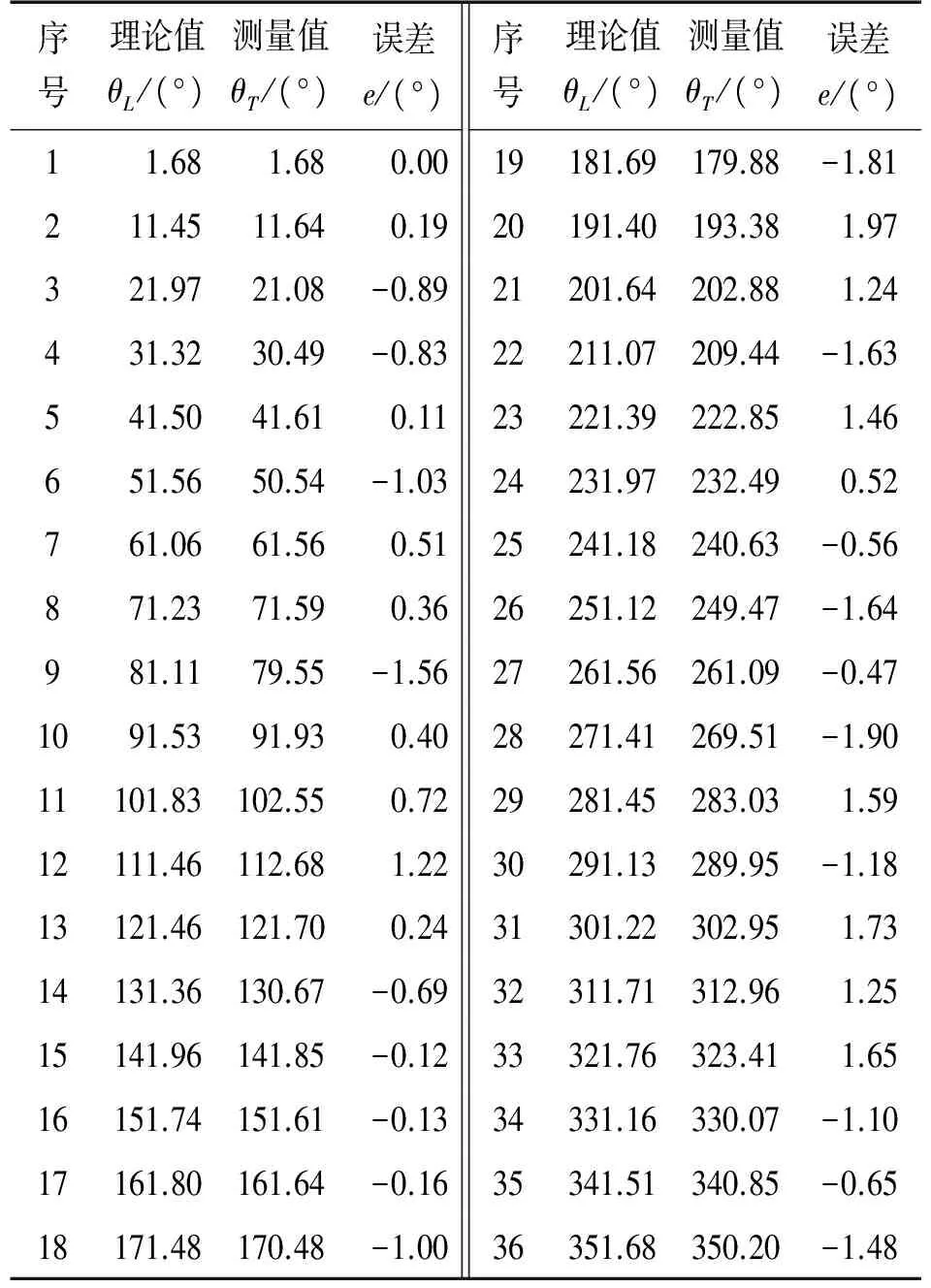
序号理论值θL/(°)测量值θT/(°)误差e/(°)序号理论值θL/(°)测量值θT/(°)误差e/(°)1 1．68 1．68 0．0019181．69179．88-1．81211．4511．640．1920191．40193．381．97321．9721．08-0．8921201．64202．881．24431．3230．49-0．8322211．07209．44-1．63541．5041．610．1123221．39222．851．46651．5650．54-1．0324231．97232．490．52761．0661．560．5125241．18240．63-0．56871．2371．590．3626251．12249．47-1．64981．1179．55-1．5627261．56261．09-0．471091．5391．930．4028271．41269．51-1．9011101．83102．550．7229281．45283．031．5912111．46112．681．2230291．13289．95-1．1813121．46121．700．2431301．22302．951．7314131．36130．67-0．6932311．71312．961．2515141．96141．85-0．1233321．76323．411．6516151．74151．61-0．1334331．16330．07-1．1017161．80161．64-0．1635341．51340．85-0．6518171．48170．48-1．0036351．68350．20-1．48

通过比较角度传感器检测数据可以看出,角度传感器检测装置具有较好的测量重复性,说明检测数据具有较高可信度。传感器最大误差为1.97°,标准偏差为0.61°,传感器精度较低,必须进行误差补偿。下面使用本文提出的基于PSO的BP神经网络补偿系统进行传感器的误差补偿。

使用表1中的奇数次检测数据作为误差补偿系统的训练数据,基于PSO的BP神经网络补偿系统的学习能力如图4所示。

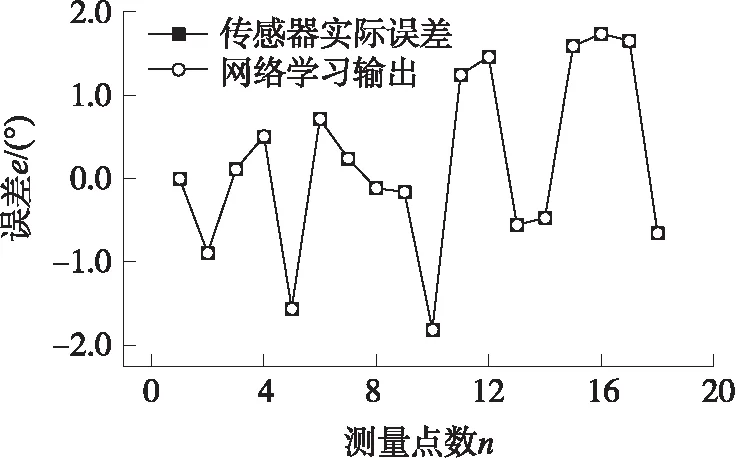
图4 基于PSO的BP神经网络学习能力

可以看出,通过使用训练数据对基于PSO的BP神经网络补偿系统进行训练后,其系统学习输出已经十分逼近了传感器的误差。

使用表1中的偶数次检测数据作为误差补偿系统的测试数据,以测试基于PSO的BP神经网络补偿系统的泛化推广能力。基于PSO的BP神经网络补偿系统的泛化推广能力如图5所示。补偿前后传感器误差如图6所示。

图6 补偿前后传感器误差对比

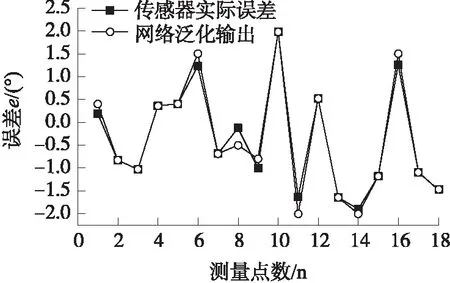
图5 基于PSO的BP神经网络泛化推广能力

可以看出,本文提出的基于PSO的BP神经网络补偿系统具有较强的泛化推广能力。通过使用补偿系统前后,传感器误差对比如图6所示,传感器的误差在零附近波动。

为了比较本文提出的误差补偿系统的优势,使用基于BP神经网络和基于多项式拟合方法的误差补偿系统对角度传感器进行误差补偿实验。BP神经网络为10×21×5结构,采用Levenberg-Marquardt迭代算法。补偿前使用BP神经网络补偿系统、多项式拟合补偿系统以及基于PSO的BP神经网络补偿系统的误差补偿效果对比如表2所示[10-11]。

表2 各补偿系统误差补偿效果对比

从实验数据可以看出,使用了本文提出的基于PSO的BP神经网络补偿系统相比补偿前,其标准偏差提高了12.5倍,最大误差和平均误差降低到9.6%和8.5%,基本能够对传感器精度误差进行补偿,并且相比于另外两种补偿方法,具有更好的误差补偿效果。另外,补偿方法的耗时也是传感器补偿算法应用时被关注的问题,尤其是在实时性要求较高的场合。多项式拟合补偿算法的编码量最低,主要通过多项式拟合公式由检测数据直接拟合得到,但是补偿精度较低。BP神经网络补偿算法的编码量较多,虽然编码量比较基于PSO的BP神经网络补偿算法少,但是由于BP神经网络使用的梯度下降算法要求具有较小的学习速度,使得算法迭代次数较多,训练过程的收敛速度较慢。基于PSO的BP神经网络补偿算法的编码量最多,不仅需要完成基本BP神经网络的模型构建,还需要通过算法完成BP神经网络的权值优化。虽然该算法编码量较多,但是由于对BP神经网络实现权值优化,加快了补偿模型训练的收敛速度。传感器误差补偿模型通常不是临时构建的,而是在线下实验室内完成对某个使用精度要求极高的传感器进行误差检测及精度补偿模型的构建,因此通常不考虑补偿模型的构建消耗的时间。通过实验研究表明,使用已建立好的误差补偿模型对传感器进行误差补偿,多项式拟合补偿模型耗时最短,BP神经网络模型时间稍长于基于PSO的BP神经网络补偿模型。

4 结论

本文针对绝对式光电编码器角度传感器的测量误差来源进行分析,确定了误差评价标准。使用基于PSO的BP神经网络作为角度传感器的误差补偿算法。使用传感器精度检测装置对一种16位绝对式光电编码器的精度进行实验,发现未补偿前,其精度较差。使用实验结果对基于PSO的BP神经网络的误差补偿系统进行训练,并对训练后的补偿系统的泛化能力和补偿能力进行测试,其结果令人满意,可以做到较好的误差补偿效果。

[1]陈兴林,刘杨,吕恒毅. 一种新型光电轴角编码器译码方法研究[J]. 传感器与微系统,2010(2):19-21,25.

[2]林靖,江伟杰,林峰. 编码器在湖上平台回转升降平移装置中的应用[J]. 传感器与微系统,2010(12):137-140.

[3]于海. 小型绝对式光电编码器动态误差检测系统及方法研究[D]. 中国科学院研究生院(长春光学精密机械与物理研究所),2014.

[4]冯英翘. 提高小型光电编码器分辨力和精度的方法研究[D]. 中国科学院研究生院(长春光学精密机械与物理研究所),2014.

[5]杜颖财,王希军,王树洁,等. 增量式编码器自动检测系统[J]. 电子测量与仪器学报,2012(11):993-998.

[6]孙莹. 小型航天级光电编码器细分误差补偿方法研究[D]. 中国科学院研究生院(长春光学精密机械与物理研究所),2010.

[7]孙艳梅,苗凤娟,陶佰睿. 基于PSO的BP神经网络在压力传感器温度补偿中的应用[J]. 传感技术学报,2014,27(3):342-346.

[8]王艳永,邓方,孙健. 改进的自适应神经模糊推理系统的角度传感器误差补偿方法[J]. 控制理论与应用,2013(10):1342-1346.

[9]张倩. 绝对式编码器误差分析与补偿系统的研究[D]. 大连海事大学,2013.

[10]洪喜,续志军,杨宁. 基于径向基函数网络的光电编码器误差补偿法[J]. 光学精密工程,2008(4):598-604.

[11]冯英翘,万秋华,孙莹,等. 小型光电编码器的高分辨力细分技术[J]. 红外与激光工程,2013(7):1825-1829.

Photoelectric Encoder Error Compensation ResearchBased on PSO-BP Neural network*

CHENHongyue*,ZHANGKun,LIUZhixiang,WANGXin

(School of Mechanical Engineering,Liaoning Technical University,Fuxin Liaoning 123000,China;)

High precision absolute photoelectric encoder is used widely,and the system precision is affected by the angle measuring precision of the photoelectric encoder. Due to the errors of the angle sensor generated in the production and the installation,the error occurs during the practical application of the photoelectric encoder,and the compensation effect of the traditional error compensation method is not good enough. Thus,an angle sensor error compensation algorithm employing BP neural network based on PSO is proposed by the paper. The experiment validation is performed,and the results show the good angle sensor error compensation effect is obtained by using the method. Compared with the uncompensated sensor,the standard deviation is elevated by 12.5 times,the maximum error and the average error is decreased to 9.6% and 8.5%,and the sensor measuring precision is promoted. The comparison test between the error compensation systems based on the traditional BP neural network,that based on the polynomial fitting method and that based on the method proposed by the paper is performed,the results show the compensation effect presented by the paper is better than other two methods.

absolute photoelectric encoder;BP neural network;particle swarm optimization algorithm;error compensation;angle sensor

陈洪月(1982-)，男，副教授，博士生导师，主要从事橡胶输送带能耗机理与节能运行技术研究工作；张 坤(1990-)，男，博士研究生，主要从事机械动态设计及仿真研究，zhangkunliaoning@163．com。

项目来源:国家自然基金项目(51404132)

2017-01-10 修改日期:2017-05-28

TP212

A

1004-1699(2017)08-1182-05

C:7230G

10.3969/j.issn.1004-1699.2017.08.009