六相永磁同步电机控制系统仿真与分析
姜俊 宋臻 朱建光
(沈阳工业大学信息科学与工程学院,辽宁 沈阳 110870)
六相永磁同步电机控制系统仿真与分析
姜俊 宋臻 朱建光
(沈阳工业大学信息科学与工程学院,辽宁 沈阳 110870)
本文首先分析六相永磁同步电机的结构及其工作原理,推导出自然坐标系下和两相旋转坐标系下的数学模型,并且在Simulink中仿真实现六相永磁同步电机数学模型及其矢量控制。仿真结果证明了所建数学模型的正确性,表明六相永磁同步电机矢量控制系统具有动态响应速度快、稳态精度高、转矩脉动小等优点。
六相永磁同步电机;矢量控制;MATLAB/Simulink;仿真
六相永磁同步电机具有结构紧凑、体积小、质量小、效率高、噪声低等优点,已被广泛应用于航空、全电力舰船推动系统等领域[1]。六相永磁同步电机是对永磁同步电机的进一步发展,它由两套三相绕组构成,相较于传统的三相永磁同步电机,它具有更多的优点[2],如空间谐波最低次数要比一般三相电机高,谐波幅值低,转矩脉动小,系统稳定性更高,效率高,并且一旦发生断相故障,系统仍然可以可靠运行[3]。
本文给出六相永磁同步电机的数学模型,并且在MATLAB/Simulink中搭建其数学模型及其矢量控制系统的模型。采用不同的运行条件对该矢量控制系统进行仿真,仿真结果证明了该模型的正确性,表明该系统具有良好的动静态性能和抗扰动性能。
1 六相永磁同步电机的数学模型
为了建立六相永磁同步电机数学模型,假设六相永磁同步电机为理想电机,并且满足下面的假设[4-5]:①忽略磁路饱和的影响,不计涡流、磁滞效应以及导体趋肤效应的影响;②忽略空间谐波磁场的影响,气隙磁场按照正弦分布;③六相永磁同步电机的转子无阻尼绕组,永磁体的磁势恒定;④不考虑频率和温度的变化对六相永磁同步电机参数的影响。
在满足上面假设条件的前提下,首先得到六相永磁同步电机在六相静止坐标系下的数学,然后根据坐标变换公式[6,7],将六相静止坐标系下的数学模型转换为两相旋转坐标系下的数学模型[8]:
电压方程:
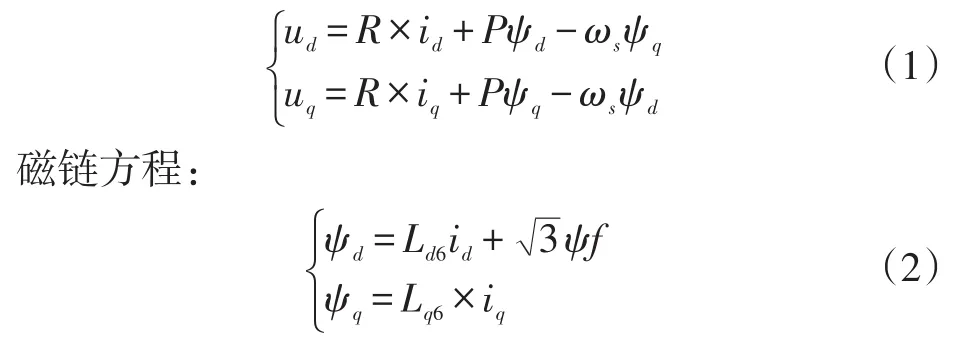
电磁转矩方程:
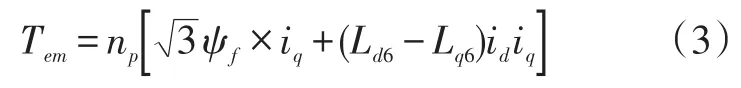
运动方程:
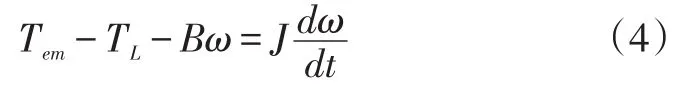
两相旋转坐标系下的六相永磁同步电机数学模型与六相静止坐标系下的数学坐标系相比较,其阶数降低了,六相永磁同步电机的磁势分量也不再是与位置角有关的函数了,这为六相PMSM的高性能控制打下坚实的基础。
2 基于id=0的矢量控制
采用电机定子电流直轴分量id=0控制,从式(3)中可以得到,当电机的极对数np和电机永磁体的磁链ψf都为一恒定值时,六相永磁同步电机的电磁转矩Tem与电流在交轴上的分量iq呈正比例关系。所以,只要控制iq的瞬时值大小就可以达到对电磁转矩的瞬时值控制的目的,在控制id=0的情况下,六相永磁同步电机的磁场转矩就只与电机定子电流的交轴分量有关,然后通过改变iq的值就可以独立控制电磁转矩,从而实现电流、磁链和转矩的解耦[9]。图1就是根据该思想构造的基于id=0的六相永磁同步电机控制系统原理图。
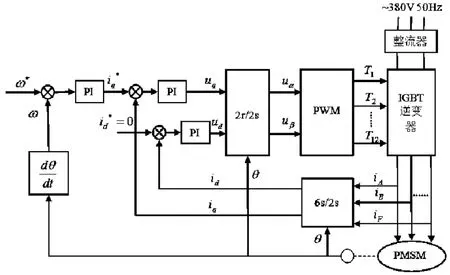
图1 基于id=0的六相永磁同步电机控制系统原理图
图1所示的六相永磁同步电机矢量系统的工作原理为:给定一额定转速ω*,该值与实际转速ω做差,然后输入速度PI调节器进行调节,PI调节器的输出值再作为电机交轴电流的给定值,同时给定直轴分量=0,将给定值的和与反馈回来的电流值同时经过电流PI调节器进行调节,调节后的值分别为交轴电压值和直轴电压值,转子永磁磁链ψf的位置角θ由光电编码器测出,该位置角θ与交轴和直轴电压值经过坐标变换后作为PWM产生模块的输入,产生PWM波形控制IGBT逆变器的导通与关断,从而得到六相定子电流的瞬时给定值,该值再经过坐标变换作为直轴和交轴的电流反馈值。
3 矢量控制系统仿真
在MATLAB/Simulink中对六相永磁同步电机矢量控制系统进行仿真,整个控制系统如图2所示,其中电机的具体参数为:电机相数为6相,极对数为11,定子电阻为0.34173Ω,永磁体磁链为0.175WB,d轴电抗为0.007 002H,q轴电抗为0.005405H,转动惯量为0.35kg/m2,阻尼系数为0N·m·s,额定转速为270r/min。
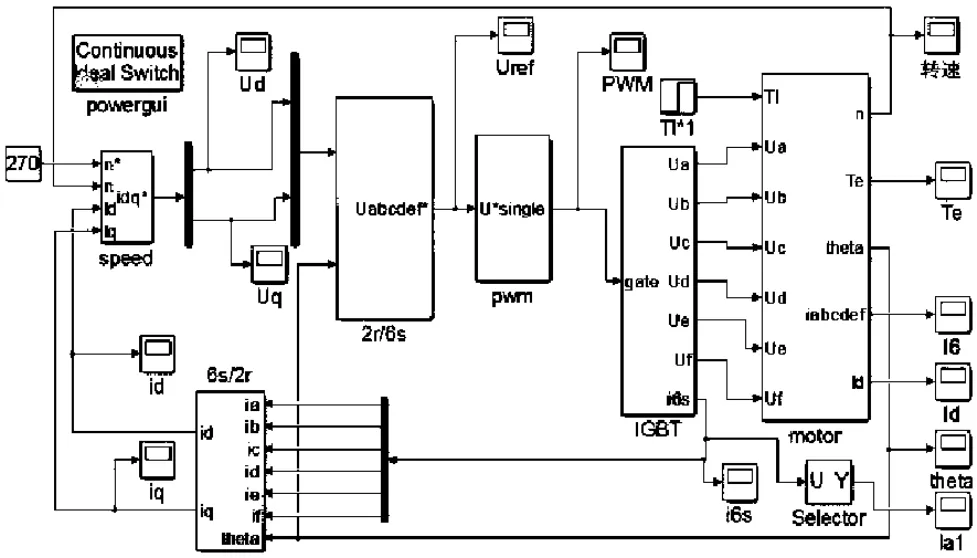
图2 六相永磁同步电机控制系统框图
六相永磁同步电机控制系统主要包括速度和电流调节模块、坐标变换模块、PWM产生模块、六相逆变器模块和六相永磁同步电机模块。
4 仿真结果分析
电机空载启动,运行平稳后,在0.4s时突加20N·m负载的转矩,仿真时间为1s,其输出转速和六相相电流如图3、4所示。
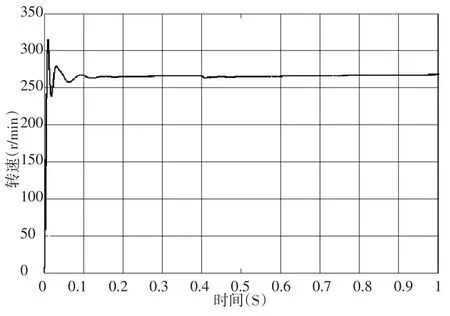
图3 输出转速曲线
从图3可以看出,达到给定速度的上升时间为0.2s左右,震荡时间短,对于在0.4s处突加负载转矩后,从速度曲线可以看出,其稳态误差很小,速度的脉动幅值也很小。
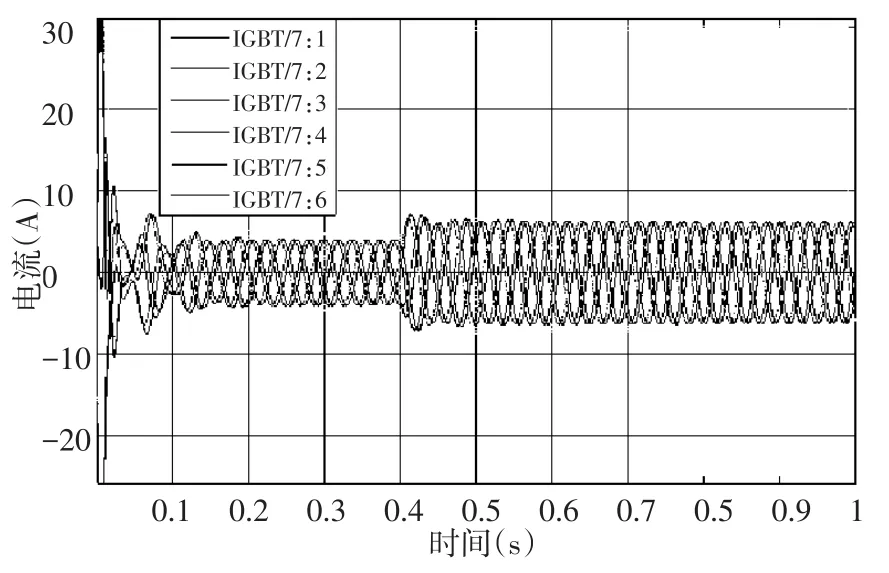
图4 六相电流波形
电机空载运行时,初始六相电流处于不断振动状态,运行一段时间后,在0.2s处波形趋于平稳,幅值在4A左右,突加负载后,六相电流有0.04s波动,但很快就再次恢复平稳状态,并且其幅值增加到6A左右。
仿真结果表明,在MATLAB/Simulink中所建立的六相永磁同步电机模型及其矢量控制系统模型具有响应速度快、抗扰动的优点。
5 结语
本文给出了六相永磁同步电机在两相旋转坐标系下的数学模型,并且在MATLAB/Simulink中建立其数学模型及其矢量控制系统模型,然后采用不同的运行条件进行仿真,仿真结果表明,该矢量控制模型仍然具有良好的动静态性能,证明其具有抗扰动的特点。
[1]付培华,陈振,丛炳龙,等.基于反布自适应滑膜控制的永磁同步电机位置伺服系统[J].电工技术学报,2013(9):288-293.
[2]E.Levi,R.Bojoi,F.Profumo,et al.Multiphase induction motor drivers–a technology status review[J].IET Elector.Power Appl.,2007(4):489-526.
[3]薛丽英,齐蓉.六相永磁同步电机驱动系统的建模与仿真[J].电力系统及其自动化学报,2006(4):49-52.
[4]唐任远.现代永磁电机理论与设计[M].北京:机械工业出版社,1997.
[5]王桐.双三相永磁同步电机空间矢量脉宽调制策略研究[D].沈阳:沈阳工业大学,2014.
[6]梁波.双Y移30度永磁同步电动机驱动系统的研究[D].长沙:湖南大学,2009.
[7]Davood Yazdani,S.Ali Khajehoddin,Alireza Bakhshai,et al.Full utilization of the inverter in split-phase drives bymeans of a dual three-phase space vector classification algorithm[J].IEEE Transactions on Industry Electoronics,2009(1):120-129.
[8]欧阳红林.多相永磁同步电动机调速系统控制方法的研究[D].长沙:湖南大学,2006.
[9]任远.双Y移30度永磁同步电机矢量控制策略研究[D].杭州:浙江大学,2012.
Simulation and Analysis of Six phase Permanent Magnet Synchronous Motor Control System
Jiang JunSong ZhenZhu Jianguang
(School of Information Science and Engineering,Shenyang University of Technology,Shenyang Liaoning 110870)
In this paper,the structure and working principle of the six-phase permanent magnet synchronous motor are analyzed.The mathematical model of the six-phase stationary coordinate system is given.Based on the coordi⁃nate transformation equation,the mathematical model of the two-phase rotating coordinate system is established. Based on MATLAB/Simulink,a simulation model of six-phase permanent magnet synchronous motor vector control system is constructed.The simulation results show that the mathematical model of the six-phase permanent magnet synchronous motor has the advantages of fast dynamic response,high steady-state precision and small torque ripple.
six phase permanent magnet synchronous motor;vector control;MATLAB/Simulink;simulation
TM359.4
A
1003-5168(2017)08-0063-03
2017-07-03
姜俊(1990-),女,硕士,研究方向:智能检测与控制技术。

