基于双通道幅相信息的空管一次雷达测高方法研究

文/方宇王娟

基于双通道幅相信息的空管一次雷达测高方法研究

文/方宇1王娟2

空管一次雷达是现代空中交通管制系统中的重要组成部分，在世界各地得到广泛应用。目前国内外的空管一次雷达均为两坐标体制，可以获得目标距离和方位信息，但不能获得目标高度或仰角信息。本文针对空管一次雷达具备高低双波束和双接收通道的特点，提出了基于双通道幅度、相位信息的空管一次雷达测高方法，以解决雷达测高中常见的多值解问题，并使用实测数据对该方法进行了验证，取得了较高的测高精度。

空管一次雷达 比幅测高 比相测高

1 引言

空中交通管制的任务是通过掌握飞机的飞行轨迹和飞行意图，发出指令，防止飞机之间的碰撞或航路阻塞，保障每个航班从起飞机场经航路到达目的地机场的秩序和飞行安全，维护并加快空中交通的有序流动。20世纪50年代开始的空管一次雷达和随后出现的空管二次雷达，使空中交通管制由程序管制发展为雷达管制，实现了对空中交通更为有效和可靠的实时管制。

从20世纪90年代开始，国际上出现了大量全固态、可无人值守的空管一次雷达，如美国雷声公司的ASR23SS雷达和法国泰勒斯公司TRAC2000N、TRAC NG雷达等，均代表了国际上的最高水平。近年来，国产空管一次雷达已研制成功，并且在民航机场得到了应用。由于空管一次雷达对可靠性的要求非常高，因此国内外的这些空管一次雷达均为使用赋形反射面天线的两坐标雷达，发射波束在俯仰上为宽波束，只能测量空中目标的距离和方位，不能获取目标的仰角和高度信息。

由于空管一次雷达缺乏获取目标高度的能力，在实际使用中通常需要和二次雷达配合使用，利用合作目标应答信号中的高度信息实现对目标的引导。这样增加了设备量和成本，同时还无法获取非合作目标的高度信息。因此，在现有空管一次雷达架构下进行测高研究不仅具有科学意义，而且有着重要的实用价值。

矫志宁和陶晶提出了利用目标幅度和距离变化信息进行两坐标雷达测高的方法，该方法的制约条件较多，需要目标等高度飞行、高信噪比以及长时间积累，因此应用场景受限。严俊坤等人提出了通过测量运动目标的距离、方位和多普勒信息来实现两坐标雷达目标的三维定位算法，该算法同样需要很长的观测时间，同时要求目标保持匀速直线运动。陈磊和方青提出了一种基于波束增益差的两坐标雷达估高方法，但是该方法在仰角大于6度时，波束增益差将出现多值模糊现象，因此只能用于低仰角的测角。

本文针对空管一次雷达具备高、低波束两个独立接收通道的特点，对双通道比幅测高、比相测高算法的原理和精度进行了分析，进而提出了比幅比相结合的两坐标雷达测高方法。使用实测数据对测高方法进行了验证，结果显示该方法解决了雷达测高中常见的多值问题，同时获得了较高的测高精度。

2 空管一次雷达测高原理

空管一次雷达的天线为赋形双弯曲反射面天线，具有较宽的频带，水平面是低副瓣窄波束，垂直面为宽的余割平方波束。为了满足仰角和高度覆盖要求，使用了两个馈源喇叭，用于形成高、低波束。与低波束对应的馈源喇叭（简称低波束馈源）的相位中心位于反射面的焦点上，且位于高波束馈源的上方。以法国泰勒斯公司的TRAC NG型空管一次雷达为例，其天线系统如图1所示。

图中的低波束馈源具备分时发射和接收电磁波的功能，高波束馈源仅接收反射面收集到的电磁波。两个馈源接收到的射频信号经过两套独立的馈线系统同时传送给两路雷达接收机。

高、低波束馈源的位置差异导致它们的接收波束方向指向不同，因此对于同一目标，高低波束接收增益不同。根据TRAC NG雷达的公开的天线参数使用高频结构仿真软件（HFSS）进行仿真，得到高低波束的俯仰面接收增益方向图如图2。

对于不同目标，由于雷达反射面积（RCS）、距离、仰角等差异，回波信号幅度不同，不能直接根据信号幅度大小确定目标仰角或高度。但高低波束通道接收到的同一目标回波信号的幅度差则只与图2中的高低波束增益差有关。对图2中的两个增益曲线作差，可以得到回波幅度差，也就是比幅值和目标仰角的对应关系，如图3所示。图3通常称之为比幅角敏函数曲线。对于空管一次雷达，得到高低波束回波比幅曲线后，再根据比幅角敏函数，就可以得到目标的仰角。

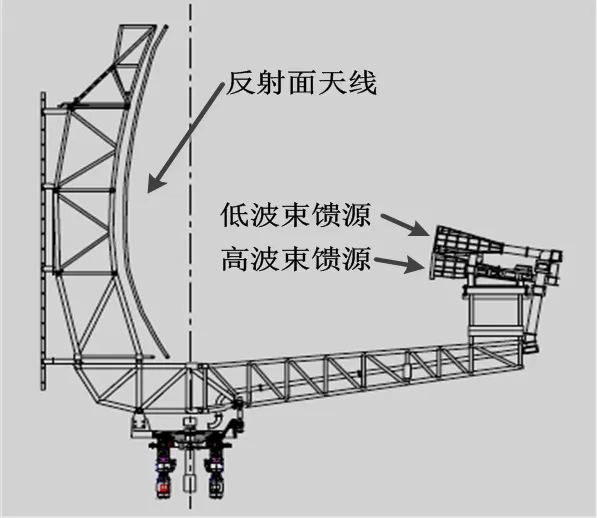
图1：TRAC NG型空管一次雷达天线系统

类似比幅角敏函数，利用高低波束回波之间的相位差，也就是比相值和目标仰角之间的对应关系，还可以得到比相角敏函数曲线。根据比相值和比相角敏函数，理论上也可以得到目标的仰角值。

测得目标仰角后，结合雷达获得的目标距离信息，根据下式可以得到目标的高度。

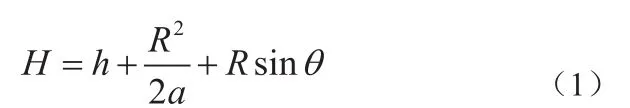
其中h为雷达天线架高，a为等效地球半径，取8493km，R为目标距离，θ为目标仰角。目标仰角与高度是一一对应的关系，并且在不考虑测距误差的情况下，测高精度只与测角精度有关，因此后文将通过研究空管一次雷达的测角方法和精度来解决两坐标雷达测高问题。

3 基于幅度相位信息的空管一次雷达测高方法

3.1 高精度角敏函数拟合

空管一次雷达的仰角信息是通过角敏函数得到的，因此高精度的角敏函数是精确测角的前提条件。图3中的比幅角敏函数为根据HFSS软件仿真得到，与实际雷达的角敏函数有一定的出入。一般需要进行天线的“方位-仰角-增益”三维方向图测试，以得到较为准确的角敏函数。天线方向图测试分为微波暗室的近场测试和距离天线几千米的室外远场测试两种。根据这两种测试结果得到的角敏函数没有充分考虑大气衰减、多径传输等因素对回波幅度、相位的影响，因此仍然不够精确。同时这两种方向图测试方法对测试条件要求很高。

本文对空管一次雷达高、低波束接收通道目标回波的幅度、相位数据进行了采集，并利用合装的空管二次雷达提供的目标高度信息计算出目标仰角，作为仰角真值，进行数据拟合，以获取高精度的角敏函数。

实测350个目标点的比幅-仰角散点图如图4所示，纵坐标为目标低波束回波幅度与高波束回波幅度的差值，横坐标为目标仰角，其分布区间为0-10度。

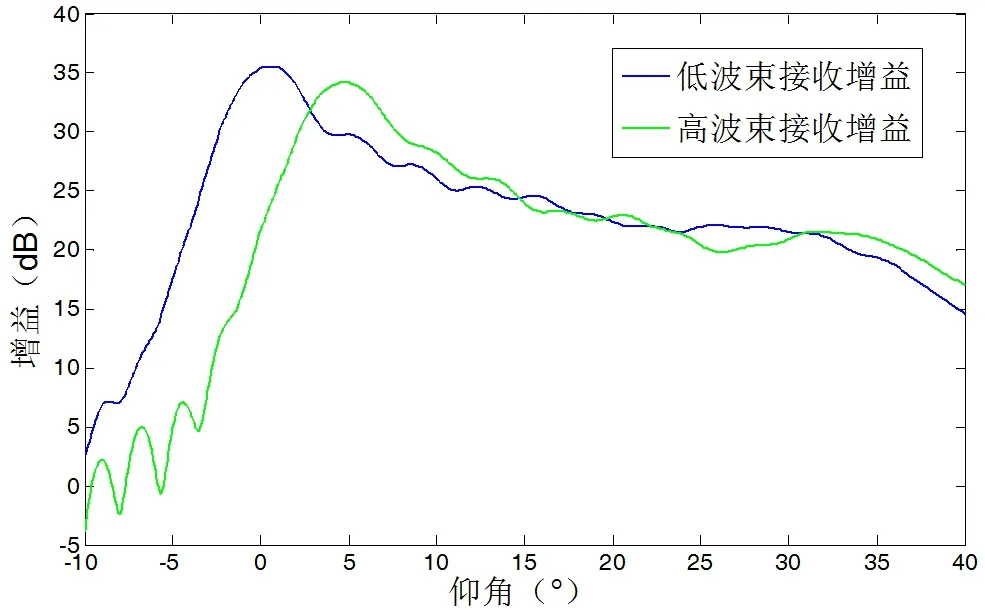
图2：高低波束俯仰面增益仿真图

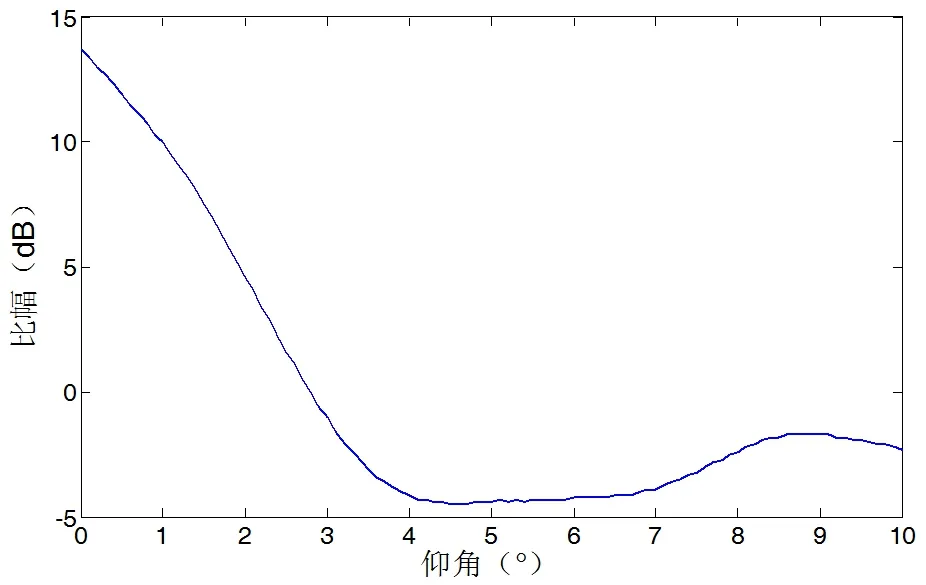
图3：比幅角敏函数曲线仿真图

图4：比幅-仰角散点分布和拟合的比幅角敏函数

表1：比幅比相结合方法测角精度（点迹信噪比足以形成航迹）

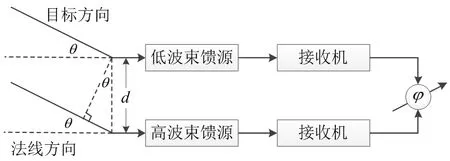
图5：比相测角示意图

从图4中可以看到，有一小部分点分布得很离散，这些点的回波信号很可能受到杂波或者异常干扰，若参与拟合，将会影响角敏函数精度。因此拟合过程共进行了两次，第一次拟合后，计算得到拟合残差的均方根值（RMSE）。然后在350个目标点中剔除拟合残差绝对值过大的点，对剩下的点进行第二次拟合。使用多项式进行最小二乘曲线拟合，拟合函数如下，其中n为阶数。

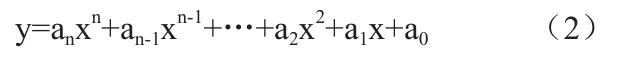
拟合阶数过低，则拟合精度不够，阶数过高，则会出现过拟合现象。根据RMSE值选取6阶拟合的第二次拟合曲线作为比幅角敏函数。如图4所示，图中拟合残差小于1.6。

类似的，可以进行比相角敏函数的拟合。空管一次雷达比相测角是利用高、低波束馈源所接收回波信号之间的相位差进行俯仰面上的测角。

如图5所示，设在θ方向有远区目标，则到达接收馈源的雷达回波近似为平面波。高、低波束馈源间距为d，它们收到的回波信号由于存在ΔR的波程差而产生相位差φ，根据图5可以得到：

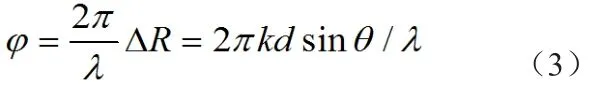
其中λ为雷达波长，k为系数，其含义为赋形天线高低波束馈源的等效相位中心与物理间距之间的比值。从上式可以看到，在目标仰角较低时，由于sinθ约等于θ，比相值φ与θ近似线性。因此在进行比相角敏函数拟合时可以使用一次函数进行拟合。350个目标点的比相-仰角散点分布和拟合的比相角敏函数见图6，图中用小三角表示的点为第一次拟合残差过大的点，不参与二次拟合，得到的比相角敏函数为图中的三段线段。

3.2 比幅比相测角精度分析

假设空管一次雷达高低波束通道的噪底幅度相当，则信噪比差即为高低波束比幅值。设低波束和高波束通道接收到的归一化信号功率（单位噪声功率时的信号功率）分别为n1和n2，有SNR1=10lgn1，SNR2=10lgn2，比幅值可表示为SNR1-SNR2。由图4可知，比幅值的测量误差将直接导致比幅测角误差，其关系式为：

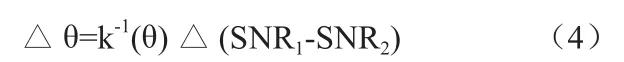
其中k(θ)为图4中比幅角敏函数在仰角θ处的斜率。为对比幅误差作进一步分析，假设图7中OS1和OS2分别为低、高波束不含噪声的信号幅度真值，有为叠加在低波束信号上的噪声，有|S1N1|=1，相对信号的相位为ω1，低波束实际接收到的信号幅度为ON1，功率的测量误差为：

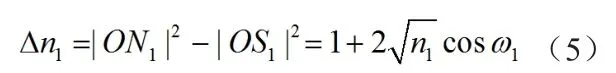
根据式（4）和式（5），可以得到由于信噪比导致的比幅测角误差为：

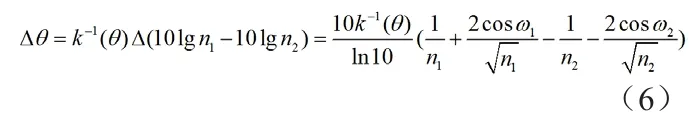
假设噪声相位ω1和ω2在[0,2π]内均匀分布，且相互独立，可以得到比幅测角误差的均值、方差如下：

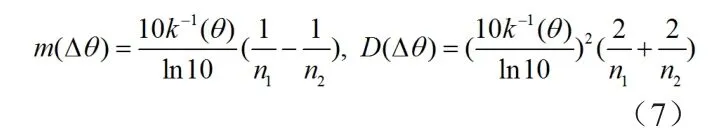
得到标准差作为测角精度的误差估计：

对于比相测角，在目标仰角较低时，根据式（3）和图7可以得到：

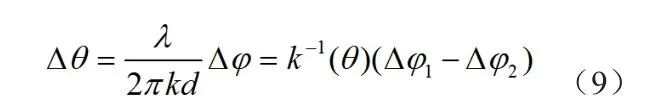
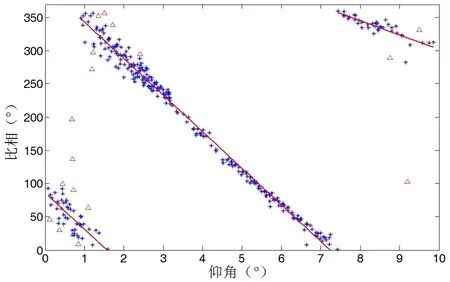
图6：比相-仰角散点分布和拟合的比相角敏函数

式（9）给出了比相测角时，仰角误差与比相误差之间的关系。比相误差与两个波束的信号相位误差相关，从图7中可见，信号相位误差同样由信噪比决定。式（9）中k(θ)为图6中比相角敏函数在仰角θ处的斜率，理论上与雷达波长、馈源间距以及馈线等效相位中心与间距的比例系数有关。

图7中，由于信号幅度远大于噪声幅度，因此相位误差Δφ1角度很小，有：

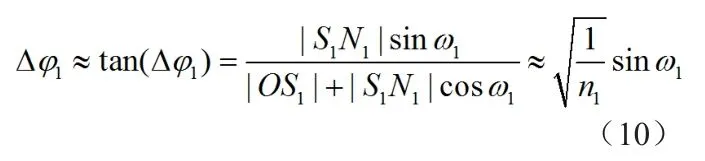
根据式（9）和式（10），可以得到由于信噪比导致的比相测角误差如下，由于式（10）得到的相位误差单位为弧度，这里进行了弧度角度转换。

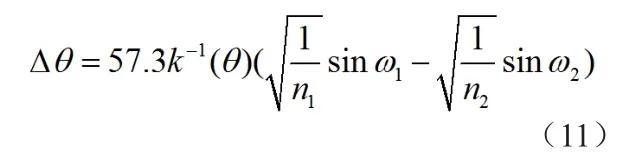
同样假设噪声相位ω1和ω2在[0,2π]内均匀分布且相互独立，可以得到比相测角误差的均值、方差如下：

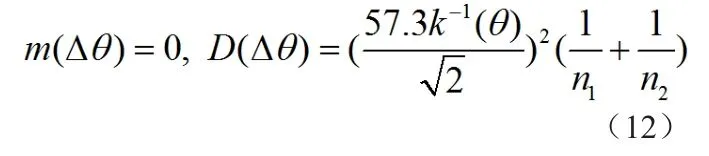
得到标准差作为比相测角精度的误差估计：

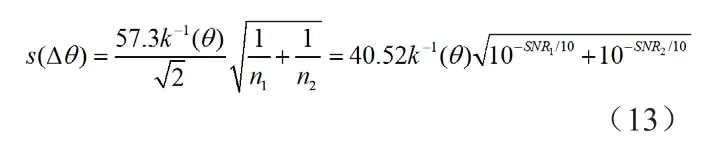
对照式（8）和式（13），即可对比幅测角和比相测角的精度进行对比。根据图4，比幅角敏函数斜率约为5；根据图6，比相角敏函数斜率约为50。式（8）与式（13）的比值为1.5，说明比幅测角精度不及比相测角，误差约为后者的1.5倍。

3.3 比幅比相结合的测高方法

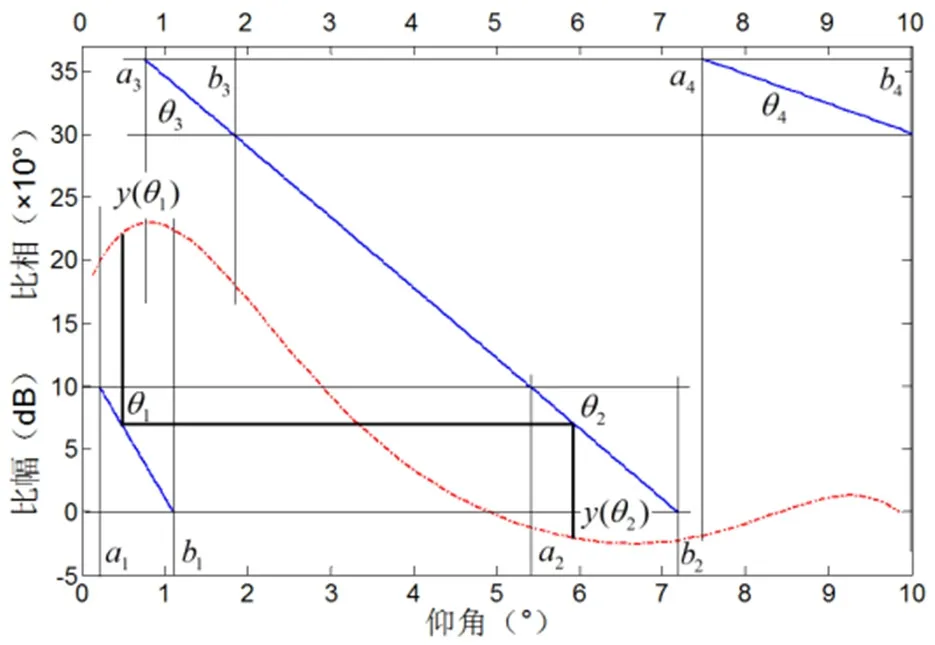
理论上，空管一次雷达通过双波束通道信号比幅或比相都能够测得目标仰角。但实际上不论是比幅测角，还是比相测角都存在多值解的问题。以比幅测角为例，当计算得到比幅值为20dB时，根据图4中的比幅角敏函数，可以在0-1度区间内、1-2度区间内分别找到一个仰角与20dB的比幅值对应。此时出现了仰角模糊现象，无法通过比幅值确定目标真实仰角。

测角多值模糊问题的数学含义为，虽然式（2）中的函数为单值函数，即对每一个输入值x（仰角），函数值y（比幅）唯一，但是其逆函数却是一个多值函数，对于某个比幅值，可能对应多个仰角值。

本文基于使用实测数据仿真得到的高精度比幅、比相角敏函数，提出了综合利用两个角敏函数，来解仰角模糊的新方法。具体来说，由于理论上比相测角精度更好，因此仰角测量值采信比相测角的结果，当比相测角出现多值解时，取多个解当中与比幅测角结果最接近的解作为目标仰角。

观察图8同中的空管一次雷达比幅、比相角敏函数曲线。根据比相角敏函数，当比相值在0-100度时，对应了a1b1之间的θ1，和a2b2之间的θ2两个仰角值，但是根据比幅角敏函数，多值解θ1对应的比幅值y(θ1)超过20dB，而多值解θ2对应的比幅值y(θ2)则小于0dB，两者差异明显，可用于消除多值解。若此时实测的比幅值与y(θ1)接近，则有理由认为真实仰角为θ1，反之，则真实仰角为θ2。当比相值为300-360度时的解模糊方法与此类似。

具体步骤如下：

第一步：拟合得到高精度的比幅比相角敏函数，并计算待测目标的比相值X，比幅值A；

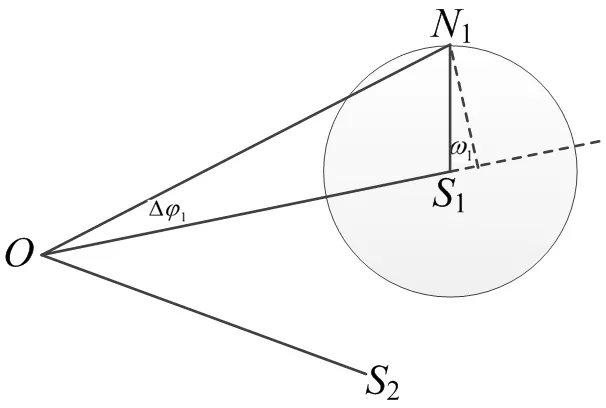
图7：噪声对回波幅度相位的影响

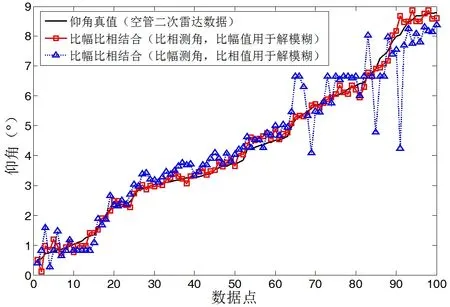
第二步：根据比相角敏函数得到唯一或多个仰角值。当0

第三步：利用比幅角敏函数解模糊，得到唯一仰角值。当0

测角流程图如图9所示。

理论上，以比幅测角结果为基准，使用比相值用于解比幅测角模糊，也能够得到仰角的唯一解。但根据前面的理论分析，比幅测角的精度要低于比相测角。另外，比幅角敏函数为近似高阶曲线，模糊区间多，解模糊算法更加复杂。

3.4 实测数据分析结果

使用350个实测数据点进行拟合，得到高精度的比幅、比相角敏函数后，再使用空管一次雷达进行一段长时间的对空探测，并记录数据。从数据中随机挑选100个能够形成航迹点的点迹用于测高方法验证。同时利用配套的空管二次雷达得到的目标仰角信息作为真值。

验证方法严格按照图9的流程进行，验证所提出的比相测角，并使用比幅值用于解仰角多值模糊的可行性，并统计了最终的测角精度。同时也给出了比幅测角，使用比相值解模糊得到的测角结果。验证结果如图10所示。两种算法误差绝对值平均值和均方根误差见表1。

从表1可以看到，比相测角比幅解模糊方法的测角精度很高，均方根误差达到了0.18度。比幅测角比相解模糊方法的精度较差，均方根误差为0.65度，并且从图10中可以看到，比幅测角比相解模糊方法在一小部分点出现了较大误差，通过分析数据发现，这些误差不是由于解模糊错误导致的，而是因为测得的比幅值误差较大，这说明比幅值相对于比相值更容易受到杂波或者干扰的影响，产生较大的畸变，从而导致测角不准。实测数据验证了前面的理论分析，比相测角精度要优于比幅测角。

图8：比幅比相角敏函数解模糊示意图

图9：比幅比相结合测角流程图

图10：比幅比相结合方法测角结果

比相测角比幅解模糊方法均方根误差小，并且没有出现误差很大的点，这说明利用比幅信息完全解决了仰角模糊的问题，因为根据图8中的比相角敏函数，一旦解模糊错误，将会导致远大于1度的误差。

4 结束语

本文针对空管一次雷达，提出了双通道比幅、比相结合的测高方法，解决了雷达测高中常见的多值解问题。使用比相测角得到唯一或模糊解后，利用比幅值解模糊，得到仰角测量值，实测数据的测角误差仅为0.18度。这说明类似空管一次雷达这样的双通道两坐标雷达，使用本文提出的方法进行测角测高是完全可行的，此方法不需要额外增加硬件设备，仅通过软件改进即可扩展两坐标雷达的使用功能，使得空管一次雷达不需要空管二次雷达配合，独立对空中目标进行三坐标引导成为了可能，具有很高的应用价值。由于实测数据只分布在0-10度仰角的空域中，因此所提出的方法以及分析验证都是针对0-10度仰角区间的进行的，实际上本文提出的方法对于10度以上的高仰角同样适用。

[1]陈磊,方青.一种基于波束增益差的两坐标雷达估高方法[J].舰船电子对抗,2015,38(04)：33-39.

[2]洪蕾,张焱,方立军.一种现代航管雷达接收/信号产生系统的研制[J].电子技术与软件工程,2016(13)：46-47.

[3]乐意.基于合成导向矢量的超分辨技术在米波雷达中的应用[J].电子技术与软件工程,2015(14)：152-153.

[4]矫志宁,陶晶.两坐标雷达测高方法研究[J].现代雷达,2011,33(12)：18-21.

[5]严俊坤,夏双志,戴奉周,刘宏伟,保铮.基于单部两坐标雷达的目标三维定位算法[J].电波科学学报,2013,28(03)：405-424.

[6]谢辉,王守杰,江晶,韩正国.信噪比对比相测高精度的影响分析[J].空军雷达学院学报,2009,23(02)：106-108.

作者单位
1.南京电子技术研究所 江苏省南京市210039
2.空军驻沪宁地区军事代表室 江苏省南京市 210039

方宇（1988-），男，安徽省桐城市人。博士学位。现为南京电子技术研究所工程师。主要研究方向为地面雷达总体设计。