环上强保持k-Jordan乘积的映射

齐霄霏，王胜利

(山西大学 数学科学学院,山西 太原 030006)

环上强保持k-Jordan乘积的映射

齐霄霏，王胜利

(山西大学 数学科学学院,山西 太原 030006)

对于任意给定的正整数k≥1,环R上的元x,y的k-Jordan乘积定义为{x,y}k={{x,y}k-1,y}1, 其中{x,y}0=x,{x,y}1=xy+yx.假设R是含有单位元与非平凡幂等元的环,f∶R→R是满射。文章证明了在一定的假设条件下,f满足{f(x),f(y)}k={x,y}k对所有的x,y∈R成立当且仅当f(x)=λx对所有的x∈R成立,其中λ∈Z(R)(R的中心)且λk+1=1.作为应用,给出了素环与von Neumann代数上保持此类性质映射的完全刻画。

Jordan乘积；k-Jordan乘积；素环；von Neumann代数

0 引言

令R是一个结合环。对任意x,y∈R和正整数k,定义x,y的k-交换子为[x,y]k=[[x,y]k-1,y],其中[x,y]0=x,[x,y]1=[x,y]=xy-yx是通常的Lie乘积(参见文献[1])。假设f∶R→R是一个映射。称f保持k-交换性, 若对任意x,y∈R, 当[x,y]k=0时有[f(x),f(y)]k=0成立;强保持k-交换性,若对任意x,y∈R有[f(x),f(y)]k=[x,y]k成立。显然, 强保持k-交换性的映射定保k-交换性, 反之不然。各种环与代数上刻画保k-交换性或强保k-交换性映射的问题已吸引了国内外许多学者的关注。对于k=1的情形,可参见文献[2-6]以及里面的参考文献。对于k>1的情形, 文献[7]给出了素环上强保持2-交换性的非线性满射的结构, 证明了含有单位元与非平凡幂等元的素环上这样的映射具有形式a|→αa+μ(a),其中μ为任意中心值映射,α属于R的可扩展中心且满足条件α3=1.文献[8]则给出了标准算子代数上强保持k-交换性的一般映射的具体形式。

另一方面,R还可被赋予另外一类乘积-Jordan乘积. 对任意x,y∈R, 记{x,y}=xy+yx为x与y的Jordan乘积。Jordan乘积是算子代数上一类重要的乘积,已有许多学者对这类乘积进行了研究(见文献[9-14]及里面的参考文献)。

受k-交换子概念的启发, 对任意正整数k,我们可以类似地定义k-Jordan乘积为{x,y}k={{x,y}k-1,y}1, 其中{x,y}0=x,{x,y}1=xy+yx.显然,当k=1时,k-Jordan乘积即为通常的Jordan乘积。此外,若映射f∶R→R满足{f(x),f(y)}k={x,y}k对任意元x,y∈R成立,则称f强保持k-Jordan乘积。于是,一个自然的问题是如何刻画强保持k-Jordan乘积的映射。本文的目的是在一般环上给出强保持k-Jordan乘积满射的具体刻画。

首先给出环的特征的定义。环R的特征为n是指,对任意x∈R,存在最小的正整数n使得nx=0成立。如果这样的n不存在, 则称R的特征为0。

下面是本文的主要结果。

定理1 令R是含有单位元1与非平凡幂等元e的特征不为2的环, 且R满足条件aRe={0}蕴含a=0与aR(1-e)={0}蕴含a=0.假设f∶R→R是满射,k为任意正整数。则f强保持k-Jordan乘积, 即f满足{f(x),f(y)}k={x,y}k对所有的x,y∈R成立,当且仅当f(x)=λx对所有的x∈R成立,其中λ∈Z(R)(R的中心)且λk+1=1.

回忆称环R是素的, 如果对任意的a,b∈R,aRb={0}蕴涵a=0或b=0. 显然, 素环一定满足定理1中的假设条件“aRe={0}蕴含a=0与aR(1-e)={0}蕴含a=0”.这样,作为推论,立即可得下面的结果。

推论2 令R是含有单位元与非平凡幂等元, 且特征不为2的素环。假设f∶R→R是满射,k为任意正整数。则f强保持k-Jordan乘积当且仅当f(x)=λx对所有的x∈R成立,其中λ∈Z(R)(R的中心)且λk+1=1.

假设M是没有I1型中心直和项的von Neumann代数。由文献[15]知,M亦满足定理1中的假设条件“aMe={0}蕴含a=0与aM(1-e)={0}蕴含a=0”.因此, 下面的推论也是显然的。

推论3 令M是没有I1型中心直和项的von Neumann代数。假设Φ∶M→M是满射。则Φ满足{Φ(A),Φ(B)}k={A,B}k对所有A,B∈M成立当且仅当Φ(A)=λA对所有A∈M成立, 其中λ∈且λk+1=1.

1 主要结果的证明

在给出本文主要结果定理1的证明之前, 首先给出下面的引理。

引理4 ([15,引理3.2])令R是含有单位元1与非平凡幂等元e的环,a∈R.假设R满足条件aRe={0}蕴含a=0与aR(1-e)={0}蕴含a=0.若exeae=eaexe对所有的x∈R成立, 则存在λ∈Z(R)使得eae=λe.

接下来我们给出定理的证明.

定理1的证明 充分性显然。对于必要性,分几步证之。

记e1=e,e2=1-e.则R可以分解为R=R11+R12+R21+R22,其中Rij=eiRej,i,j∈{1,2}.

以下总假设f∶R→R是强保持k-Jordan乘积的满射. 由f的满射性知,

存在元t∈R使得f(t)=1.

(1)

第一步f是可加的, 即对任意元x,y∈R,有f(x+y)=f(x)+f(y).

对任意的元x,y∈R, 利用等式(1), 我们有

2k(f(x+y)-f(x)-f(y))=

{f(x+y),1}k-{f(x),1}k-{f(y),1}k={x+y,t}k-{x,t}k-{y,t}k=0,

即得2k(f(x+y)-f(x)-f(y))=0.由于R的特征不为2,该式蕴涵f(x+y)=f(x)+f(y)对所有的x,y∈R成立, 即f是可加的。

第二步f(ei)∈Rii且f(ei)k+1=ei,i=1,2.

这里仅给出i=1时的证明, 对于i=2的情形类似可证。

首先,由于{f(e1),f(e1)}k={e1,e1}k,我们有2kf(e1)k+1=2ke1.因为R的特征不为2,所以

f(e1)k+1=e1.

(2)

以下为讨论方便,记f(e1)=s=s11+s12+s21+s22与t=t11+t12+t21+t22,其中t为等式(1)中的元。注意到

在上式左右两边分别乘以e2, 利用R的特征不为2的性质, 可得e2ske2=0. 该式结合等式(2), 有

e1=ssk=se1ske1+se1ske2+se2ske1

(3)

和

e1=sks=e1ske1s+e1ske2s+e2ske1s.

(4)

在式(3)左右两边分别乘以e1, 得到

e1=s11e1ske1+s12e2ske1;

(5)

在等式(3)与等式(4)左右两边分别乘以e1与e2, 可得

s11ske2=0,e1ske1s12+e1ske2s22=0;

(6)

在等式(4)左右两边分别乘以e2, 可得

e2ske1s12=0.

(7)

现结合等式(5)-(7), 有

s12=s11e1ske1s12+s12e2ske1s12=s11e1ske1s12=-s11e1ske2s22=0.

类似可证s21=0.因此f(e1)=s=s11+s22.

并注意到R的特征不为2, 可得r11=r12=r21=0, 即得f(r22)=x22. 特别地,

存在u22∈R22使得f(u22)=e2.

现利用等式

与R的特征不为2这一性质,即得s22=0.因而f(e1)=s11∈R11.该步得证。

第三步f(Rii)⊆Rii,i∈{1,2}.

任取x11∈R11,令f(x11)=s11+s12+s21+s22.利用第二步,有

2kx11={x11,e1}k={s11+s12+s21+s22,e1f(e1)e1}k=

s11(e1f(e1)e1)k+s21(e1f(e1)e1)k+(e1f(e1)e1)ks11+

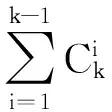
此式蕴含(e1f(e1)e1)ks12=s21(e1f(e1)e1)k=0. 该式再结合第二步即得s12=s21=0.

另一方面, 对e2, 已证存在u22∈R22使得f(u22)=e2. 进而有

此蕴含s22=0. 因而f(x11)=s11∈R11.

类似可证f(R22)⊆R22.

第四步 对任意元xij∈Rij(1≤i≠j≤2),我们有f(x12)=f(e1)x12与f(x21)=x21f(e1).

仍然只给出情形{i=1,j=2}的证明,另一情形类似可证。

任取x12∈R12,并令f(x12)=s11+s12+s21+s22.利用f的定义与第一步可知

x12={x12,e1}k={s11+s12+s21+s22,e1f(e1)e1}k=

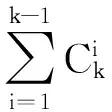
上式蕴含x12=(e1f(e1)e1)ks12与s21(e1f(e1)e1)k=0.进而得到s12=e1f(e1)e1x12且s21=0.

另一方面, 注意到

此式与R的特征不为2这一性质蕴含s22=0.

2kr22+r12+r21={r,e2}k={e1,e2f(e2)e2}k=0.

此蕴含r22=r12=r21=0. 因此f(r11)=e1. 现在, 结合上面已证等式,有

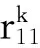
此式与事实R的特征不为2蕴含s11=0. 该步成立。

第五步 存在元λ∈Z(R)满足λk+1=1, 使得f(xij)=λxij对所有元xij∈Rij成立, 其中i,j∈{1,2}.

对任意元x11∈R11和任意元x12∈R12, 有

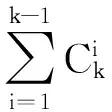
2kx11+(2k-1)x11x12.

又, 利用以上四步, 得到

{f(x11),f(x12+e1)}k={e1f(x11)e1,e1f(e1)x12+e1f(e1)e1}k=

{f(x11),f(e1)}k(e1+x12)-(e1f(e1)e1)kf(x11)x12.

结合上面两式可得

2kx11={f(x11),f(e1)}k

与

(2k-1)x11x12={f(x11),f(e1)}kx12-(e1f(e1)e1)kf(x11)x12

对任意元x11∈R11与x12∈R12成立。进而得到

[(e1f(e1)e1)kf(x11)-x11]e1xe2=0对任意元x11∈R11,x∈R成立。

现利用定理中R满足的条件可得

x11=(e1f(e1)e1)kf(x11)对任意元x11∈R11成立。

再利用第二步知

f(x11)=e1f(e1)e1x11=f(e1)x11对所有元x11∈R11成立。

(8)

类似地,利用等式{x11,x21+e1}k={f(x11),f(x21)+f(e1)}k,可证x11=f(x11)(e1f(e1)e1)k,进而有

f(x11)=x11e1f(e1)e1=x11f(e1) 对所有元x11∈R11成立。

(9)

比较等式(8)-(9),得到x11e1f(e1)e1=e1f(e1)e1x11对所有元x11∈R11成立。现由引理4知,

存在λ∈Z(R)使得e1f(e1)e1=λe1.

(10)

注意到(e1f(e1)e1)k+1=e1. 因此λk+1=1.

现在结合等式(8)与(10), 即得f(x11)=λx11; 结合等式(8)与(10)与第四步, 得到f(x12)=λx12与f(x21)=λx21.

最后, 任取x22∈R22与x21∈R21. 由以上所证等式, 有

x22x21={x22,x21+e1}k={f(x22),λ(x21+e1)}k=λkf(x22)x21,

即x22xe1=λkf(x22)xe1对所有x∈R成立。现利用定理中R满足的条件可得x22=λkf(x22), 进而得到f(x22)=λx22.

第六步 对任意元x∈R, 我们有f(x)=λx. 定理成立。

事实上,任取x∈R,结合第一步和第五步,该步显然成立。

证毕。

[1] Lanski C.An Engel Condition with Derivation for Left Ideals[J].ProcAmerMathSoc,1997,125:339-345.DOI:10.12691/jmsa-2-3-1.

[2] Brešar M，Miers C R.Commutativity Preserving Mapping of Von Neumann Algebras[J].CanadJMath,1993,45:659-708.DOI:10.4153/CJM-1993-039-x.

[3] Bell H E,Daif M N.On Commutativity and Strong Commutativity Preserving Maps[J].CanadMathBull,1994,37:443-447.DOI:10.4153/CMB-1994-064-x.

[5] Lin J S,Liu C K.Strong Commutativity Preserving Maps on Lie Ideals[J].LinearAlgebraAppl,2008,428:1601-1609.DOI:10.1016/j.laa.2007.10.006.

[6] Qi X F,Hou J C.Nonlinear Strong Commutativity Preserving Maps on Prime Rings[J].CommuAlgebra,2010,38:2790-2796.DOI.org/10.1080/00927870903071179.

[7] Qi X F.Strong 2-commutativity Preserving Maps on Prime Rings[J].PublMathDebrecen,2016,88(1-2):119-129.DOI:10.5486/PMD.2016.7270.

[8] Hou J C,Qi X F.Strongk-commutativity Preservers on Complex Standard Operator Algebras[J].LinearMultilinearAlgebra,2017.DOI.org/10.1080/03081087.2017.1330868.DOI.org/10.1080/03081087.2017.1330868.

[9] Chebotar M A,Ke W F,Lee P H,etal.On Maps Preserving Zero Jordan Products[J].MonatshMath,2006,149:91-101.DOI:10.1007/s00605-005-0371-7.

[10] Zhao L K,Hou J C.Jordan Zero-product Preserving Additive Maps on Operator Algebras[J].JournalofMathematicalAnalysisandApplications,2006,314:689-700.DOI.org/10.1016/j.jmaa.2005.04.015.

[11] Hou J C,Li C K,Wong N C.Maps Preserving the Spectrum of Generalized Jordan Product of Operators[J].LinearAlgebraandItsApplications,2010,432:1049-1069.DOI:org/10.1016/j.laa.2009.10.018.

[12] Bourhim A,Mabrouk M.Maps Preserving the Local Spectrum of Jordan Product of Matrices[J].LinearAlgebraandItsApplications,2015,484:379-395.DOI:org/10.1016/j.laa.2015.06.034.

[13] Zhang W,Hou J C,Qi X F.Maps Preserving Peripheral Spectrum of Generalized Jordan Products of Operators[J].ActaMathematicSinica,EnglishSeries,2015,31:953-972.DOI：10.1007/s10114-015-4367-5.

[14] An G Y,Li J K.Characterizations of Linear Mappings Through Zero Products or Zero Jordan Products[J].ElectronicJournalofLinearAlgebra,2016,31:408-424.DOI:https:∥doi.org/10.13001/1081-3810.3090.

[15] Qi X F,Hou J C.Characterization ofk-commuting Additive Maps on Rings[J].LinearAlgebraAppl,2015,468:48-62.DOI.org/10.1016/j.laa.2013.12.038.

Strongk-Jordan Product Preserving Maps on Rings

QI Xiaofei,WANG Shengli

(School of Mathematical Sciences,Shanxi University,Taiyuan 030006，China)

For any integerk≥1, thek-Jordan product of two elementsx,yin a ring R is defined by {x,y}k={{x,y}k-1,y}1,where {x,y}0=xand {x,y}1=xy+yx. Assume that R is a unital ring containing a nontrivial idempotent andf∶R→R is a surjective map. It is shown that, under some mild conditions,fsatisfies {f(x),f(y)}k={x,y}kfor allx,y∈R if and only if there existsλ∈Z(R) (the center of R) withλk+1=1 such thatf(x)=λxholds for allx∈R.As an application, such maps on prime rings and von Neumann algebras are characterized,respectively.

Jordan products；k-Jordan products；prime rings；von Neumann algebras

10.13451/j.cnki.shanxi.univ(nat.sci.).2017.03.002

2017-05-24；

2017-06-16

国家自然科学基金(批准号:11671006)；山西省高等学校优秀青年学术带头人支持计划

齐霄霏(1981-),女,山西阳泉人,教授,博士,研究方向:算子理论与算子代数。E-mail:qixf1981@sxu.edu.cn

O175

A

0253-2395(2017)03-0406-05