钢轨轧制不平顺对车岔耦合系统垂向动力特性的影响
马晓川,王平,徐金辉,徐井芒,陈嵘
钢轨轧制不平顺对车岔耦合系统垂向动力特性的影响
马晓川,王平,徐金辉,徐井芒,陈嵘
(西南交通大学高速铁路线路工程教育部重点实验室,四川成都,610031)
为分析某18号高速道岔轨道不平顺的产生原因,使用快速傅里叶变换的方法分析其频率分布,道岔转辙器区与辙叉区的钢轨不平顺是钢轨轧制过程中控制精度不足造成的,其主频波长为0.8 m的倍数。基于车辆−道岔耦合系统动力学理论,研究钢轨轧制不平顺对道岔区垂向轮轨力和轮重减载率的影响,并分析不同车辆通过速度条件下最大轮重减载率的变化规律。研究结果表明:车辆以350 km/h的速度通过道岔时,垂向轮轨力变化较为剧烈,其一阶主频为50.51 Hz,与全线轨道不平顺的一阶主频51.27 Hz基本相同,辙叉区最大轮重减载率超过0.8的限值,且持续时间较长,存在脱轨的可能;道岔区钢轨存在轧制不平顺时,车辆速度对最大轮重减载率影响较为显著,为保证轮重减载率不超过0.8的限值,车辆通过高速道岔时理论上应限速160 km/h,当不存在钢轨轧制不平顺时,车辆速度对最大轮重减载率的影响较小。
车辆;道岔;轧制不平顺;垂向轮轨力;减载率
轨道不平顺是轮轨系统的重要激扰源,是引起车辆振动及轮轨相互动力作用的主要原因,高速铁路工程要求所有的轨道必须具有高平顺性[1],高速道岔作为高速铁路限制列车速度的关键设备,由于其本身结构的特点,轨道不平顺在岔区显得尤为复杂和突出,主要分为结构不平顺、动力不平顺、状态不平顺和几何不平顺[2]。由于高速铁路对钢轨的平直度要求较高,因此钢轨加工时需要进行钢轨矫直工艺,在这个过程中,由于矫直工艺控制精度的不足,容易使钢轨产生轧制周期性不平顺,该不平顺属于钢轨加工导致的几何不平顺,当带有轧制不平顺的钢轨铺设到高速道岔上时,对高速道岔的垂向动力特性影响十分巨大。现阶段国内外关于钢轨轧制不平顺的研究较少,且多数研究[3−10]针对区间线路的轨道不平顺,本文作者针对高速道岔中存在的钢轨轧制不平顺,建立车辆−道岔耦合系统动力学模型,研究动车组车辆高速通过道岔时,钢轨轧制不平顺对高速道岔垂向动力特性的影响。
1 轨道不平顺谱分析
1.1 轨道不平顺测量
现场采用德国Vogel & Plötscher公司生产的RMF 2.3型波磨测量仪对存在钢轨轧制不平顺的18号高速道岔直向基本轨的表面平直度进行了测量,轨道高低不平顺测量结果如图1所示。

图1 实测轨道高低不平顺
由图1可以看出:道岔区钢轨的不平顺度要明显大于区间线路,辙叉部分的钢轨不平顺度比转辙器部分的大,导曲线部分的钢轨不平顺度状况相对较好。中国制订的350 km/h高速铁路60 kg/m钢轨供货技术条件规定钢轨竖直平直度不得超过0.3 mm/3 m及0.2 mm/1 m,很明显道岔转辙器和辙叉区的钢轨已超过了该限值,区间线路的钢轨则在容许限度内。
1.2 分析方法
本文采用快速傅里叶变换(FFT)的方法分析轨道不平顺的频率特征,快速傅里叶变换是离散傅里叶变换的一种快速算法[11]。设()为有限长的序列,其长度为,则其离散傅里叶变换如下式所示。

由傅里叶变换的定义[12]可知:信号经过傅里叶变换后得到的不是各频率分量的振幅,而是其谱密度。
将序列()作周期延拓,可用三角级数展开[13]为
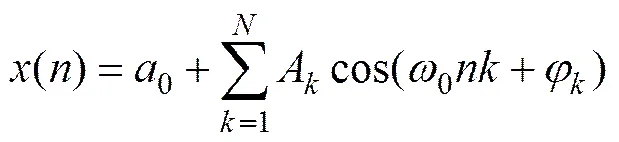
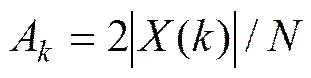
1.3 分析结果
应用上述方法,对轨道不平顺的测量结果进行频谱分析,可分别得到全线、岔前线路、转辙器部分、导曲线部分、辙叉部分及岔后线路的轨道不平顺幅值谱如图2所示。
由图2可知:从幅值上看,辙叉区不平顺的幅值最大,最大值为0.18 mm左右;转辙器不平顺的幅值略小于辙叉不平顺的幅值,最大值为0.15 mm;导曲线、岔前和岔后线路不平顺的幅值较小,最大值不足0.1 mm。从波长上看,岔前和岔后线路不平顺的波长最大,均为5 m左右;导曲线不平顺的波长次之,为3~4 m;辙叉和转辙器不平顺的波长最小,为1.6~ 2.5 m。
辙叉部分的钢轨不平顺幅值谱中,其一阶和二阶主频波长分别为2.4 m和1.6 m,转辙器部分的钢轨不平顺幅值谱中,其一阶和二阶主频波长分别为1.9 m和1.6 m,导曲线部分的一阶和二阶主频波长为4.1 m和3.1 m,均近似为0.4 m或0.8 m的倍数。
1.4 轧制不平顺产生原因
为满足钢轨平直度的要求,高速铁路钢轨在加工过程中需要进行矫直流程,目前大部分生产高速铁路钢轨的厂家采用的是复合矫直工艺,德国SMS公司的平立复合矫直机由9个平矫辊及8个立矫辊所组成,平立复合矫直机采用的是辊式矫直工艺,即钢轨通过辊式矫直机的上下两排矫直辊间进行往复弹塑性弯曲,从而达到矫直目的,钢轨矫直过程示意如图3所示,平辊主要矫正钢轨垂直方向的平直度,立辊主要矫正钢轨水平方向的平直度。第1~8个平辊直径为 1 100~1 200 mm,第9个平辊直径为600 mm,矫直辊的水平间距为1 600 mm,上下两排矫直辊的水平间距为800 mm,水平垂直间距为900~1 400 mm,最大矫直力为3 600 kN。

(a) 道岔全线;(b) 岔前线路;(c) 转辙器线路;(d) 导轨线路;(e) 辙叉线路;(f) 岔后线路
平辊水平间距正好与图3中转辙器部分和辙叉部分钢轨垂直不平顺的二阶主频波长相同;上下两排辊间的水平间距为0.8 m,而辙叉部分及导曲线部分钢轨不平顺的一阶和二阶主频波长均近似为0.8 m的整数倍。可见该道岔的不平顺为钢轨矫直过程中所产生的周期性不平顺,是平辊在上下推进过程中精度控制不足所造成的。

图3 钢轨矫直过程示意
2 仿真计算模型
参考文献[2, 14−18],建立道岔区车辆−轨道系统耦合振动模型,在该系统振动耦合模型中包括以下3个组成部分,分别是车辆模型、道岔模型和轮轨接触模型。
2.1 车辆模型
建立道岔区的车辆模型与区间线路的车辆模型相同,本文为了更好地模拟车辆通过道岔时的动力特性,采用整车模型,建立车辆模型如图4所示。
本文车辆−道岔计算模型坐标系的选取原则是:以车辆前进方向为轴的正方向,车辆前进方向的右侧为轴的正方向,轴正方向则根据右手法则来确定。

(a) 车辆立面模型;(b) 车辆侧面模型
在该车辆模型中,考虑31个运动自由度,分别是车体的横移、沉浮、侧滚、点头和摇头5个自由度;2个转向架分别考虑横移、沉浮、侧滚、点头和摇头共10个自由度,4个车轮分别考虑横移、沉浮、侧滚和摇头共16个自由度。车辆的基本计算参数包括车体、转向架及轮对的质量、绕各轴的惯性矩,一系和二系悬挂的刚度和阻尼[19]。
2.2 道岔模型
本文选取18号中国高速道岔为研究对象,该高速道岔直向允许通过速度为350 km/h,根据18号高速道岔的设计图建立道岔整体模型如图5所示。

(a) 道岔平面模型;(b) 道岔立面模型
在该道岔模型中,道岔中的每一根钢轨按轨枕支承点划分为有限个梁单元,每一个单元节点有垂向位移、垂向转角、横向位移及横向转角4个自由度,轨枕在横向上视为1个刚体质量块,具有横向位移1个自由度,在垂向上,轨枕按钢轨支承点划分为有限个梁单元,具有垂向位移和垂向转角2个自由度。
18号中国高速道岔的基本计算参数如表1所示。
2.3 轮轨接触模型
车辆模型和道岔模型通过轮轨接触模型建立关联,在轮轨接触模型中,考虑车轮与钢轨踏面的接触关系、车轮轮缘与钢轨的接触关系、车轮轮背与翼轨的接触关系,同时考虑车辆运行至道岔不同部位时接触轨迹的变化。
轮轨垂向由非线性的赫兹接触弹簧力连接,轮轨横向由轮轨蠕滑力和轮缘力等作用力进行连接,考虑车轮与基本轨、尖轨以及车轮与翼轨、心轨可能发生的多点接触情况,轮轨接触模型中考虑了轮轨接触点附近车轮和钢轨的曲率变化。

表1 道岔基本计算参数Table 1 Basic calculation parameters of turnout
2.4 振动方程
采用变分形式的最小势能原理方法,建立道岔轮轨振动系统的微分方程,由最小势能原理可知,在所有满足边界条件的协调位移中,满足平衡条件的位移可以使系统的总势能达到极值,即满足以下关系:
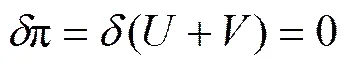
式中:和分别为系统的总应变能和总外力势能。
以大地为坐标参考系,以轨道及车辆均不受外力状态为初始状态,推导系统中各个能量的变分表达式及变分形式的位移协调条件,经计算机对号入座形成系统的质量矩阵[]、刚度矩阵[]及阻尼矩阵[],并组成系统的振动微分方程:
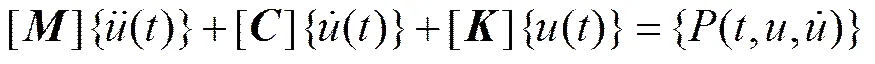
利用系统的振动微分方程,在某一时间步长下,迭代判断协调位移能否满足系统平衡条件,并重新组建新的振动微分方程,直到满足要求为止,即可得到该时刻的系统振动响应。
2.5 计算模型验证
文献[20]建立了车辆−轨道的空间振动模型,并通过与NUCARS和SIMPACK商业软件数值仿真结果的对比验证了其自编程序计算结果的可靠性。本文将通过对比分析相同条件下本文计算结果与文献[20]自编程序的计算结果,来验证本文计算模型的正确性。
车辆进入道岔前在区间线路上运行时,本文的计算结果与文献[20]自编程序计算结果的对比如图6所示。计算时车速取为160 km/h,轨道不平顺采用的是单一的谐波型高低不平顺,该不平顺可按下式进行描述:

(a) 车体垂向加速度对比;(b) 轮轨垂向力对比
1—本文计算结果;2—文献[20]自编程序计算结果。
图6 高低不平顺下计算结果对比Fig. 6 Comparison calculation results under vertical irregularities
式中:为不平顺的全峰值,取为10 mm;为不平顺波长,取为20 m;为线路的纵向距离。
由图6可见:当轨道只存在高低不平顺时,与文献[20]自编程序计算结果相比,本文计算结果中,车体的垂向加速度基本吻合,轮轨垂向力的波动范围略大,但两者的变化规律大致相同。本文的计算结果与文献[20]自编程序的计算结果较为接近,说明本文所使用的计算模型可以较为真实可靠的反映车辆−道岔耦合系统的垂向振动特性。
3 数值模拟结果及分析
本文基于车辆−道岔耦合系统动力学理论,建立了车辆−道岔耦合系统动力学模型,理论仿真动车组车辆以350 km/h的速度直向通过存在钢轨轧制不平顺的18号高速道岔,得到其垂向轮轨力及轮重减载率等系统动力响应结果;另外,动车组车辆分别以不同的速度直向通过18号高速道岔,得到其最大轮重减载率随车辆速度的变化规律,并与现场实测得到的结果进行对比分析。
3.1 垂向轮轨力
图7所示为动车组车辆以350 km/h的速度直向通过存在钢轨轧制不平顺的18号高速道岔时直基本轨侧和直向里轨侧的垂向轮轨力仿真计算结果。由图7可见:直基本轨侧的垂向轮轨力相比直向里轨侧普遍偏大,原因是钢轨轧制不平顺存在于直基本轨一侧,而直向里轨侧不存在钢轨轧制不平顺,只存在因尖轨、心轨等结构造成的结构不平顺。两侧垂向轮轨力均在转辙器部分和辙叉部分波动变化剧烈,直基本轨侧辙叉部分距尖轨尖端53.793~53.946 m和55.606~56.190 m处的垂向轮轨力均为0,说明此处车轮已脱离钢轨处于悬浮状态;而在岔前线路、导曲线部分和岔后线路,两侧垂向轮轨均较小。
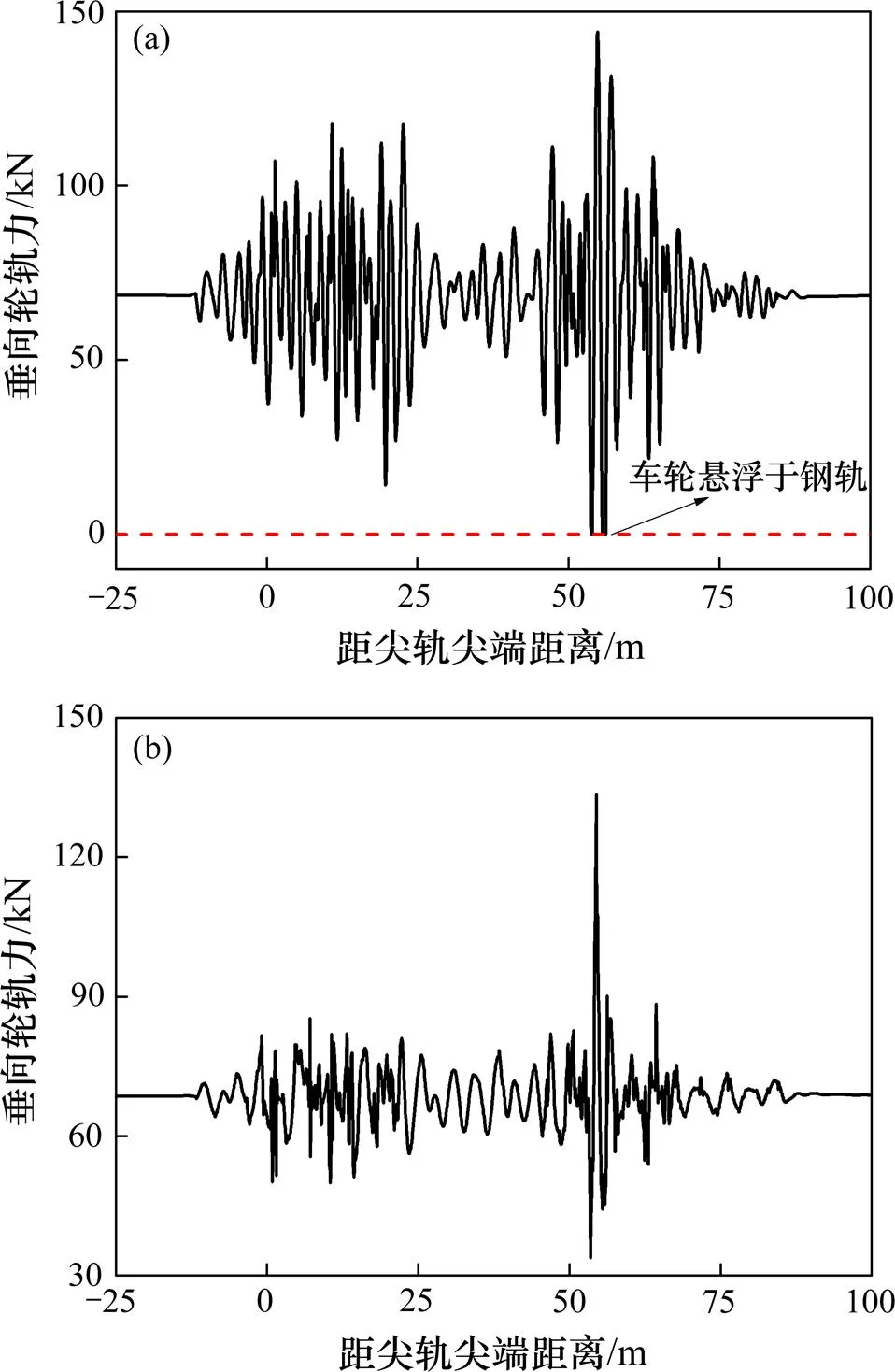
(a) 直基本轨侧;(b) 直向里轨侧
通过傅立叶变换,将图7中垂向轮轨力时域分布转化为垂向轮轨力的频域分布,图8所示为垂向轮轨力的频谱图。

(a) 直基本轨侧;(b) 直向里轨侧
由图8可以看出:直基本轨侧的垂向轮轨力一阶主频为50.51 Hz,道岔全线轨道不平顺的一阶主频波长为1.9 m,动车组车辆速度为350 km/h,换算为一阶主频为51.17 Hz,两者的一阶主频近似相等;直向里轨侧的垂向轮轨力一阶主频为30.027 Hz,与钢轨轧制不平顺的一阶主频相差较远,原因是钢轨轧制不平顺存在于直基本轨一侧,直向里轨侧主要存在道岔结构不平顺,因此其垂向轮轨力的频率分布不能表征钢轨轧制不平顺的频率特征。
3.2 轮重减载率
图9所示为理论仿真动车组车辆以350 km/h的速度直向通过存在钢轨轧制不平顺的18号高速道岔时轮重减载率的变化规律。由图9可以看出:转辙器部分的轮重减载率最大值约为0.81,辙叉部分的最大轮重减载率为1.0,两者均已超过TB 10761—2013“高速铁路工程动态验收技术规范”规定的限值0.80,导曲线部分轮重减载率最大值约为0.26,远小于转辙器部分和辙叉部分的最大轮重减载率。
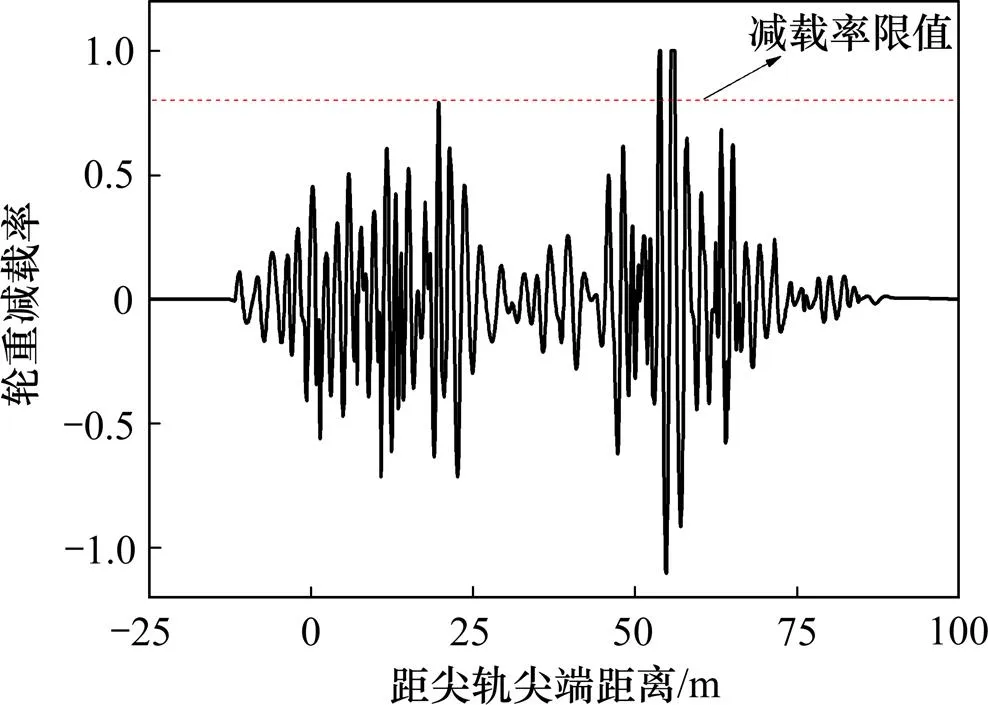
图9 直基本轨侧轮重减载率
根据钢轨轧制不平顺的频谱分析结果,转辙器部分和辙叉部分的不平顺波长远小于岔前线路、导曲线部分及岔后线路的不平顺波长,即相比岔前线路、导曲线部分及岔后线路的不平顺,转辙器部分和辙叉部分的不平顺属于短波不平顺,结合图9的分析结果,短波不平顺相比长波不平顺更容易引起轮重减载率超限。
3.3 车辆速度影响
现场实验时,在该18号高速道岔的地面布置一系列测点,如图10(a)所示,得到动车组车辆以不同的速度直向通过该道岔时最大轮重减载率的测试结果。由图10(a)可以看出:当动车组车辆速度超过350 km/h后,现场实测的轮重最大减载率将超过限值0.8。分别设定18号高速道岔存在钢轨轧制不平顺和不存在钢轨轧制不平顺2种情况下,动车组车辆分别以50,100,150,200,250,300和350 km/h的速度直向通过该道岔时,最大轮重减载率的变化规律如图10(b)所示。
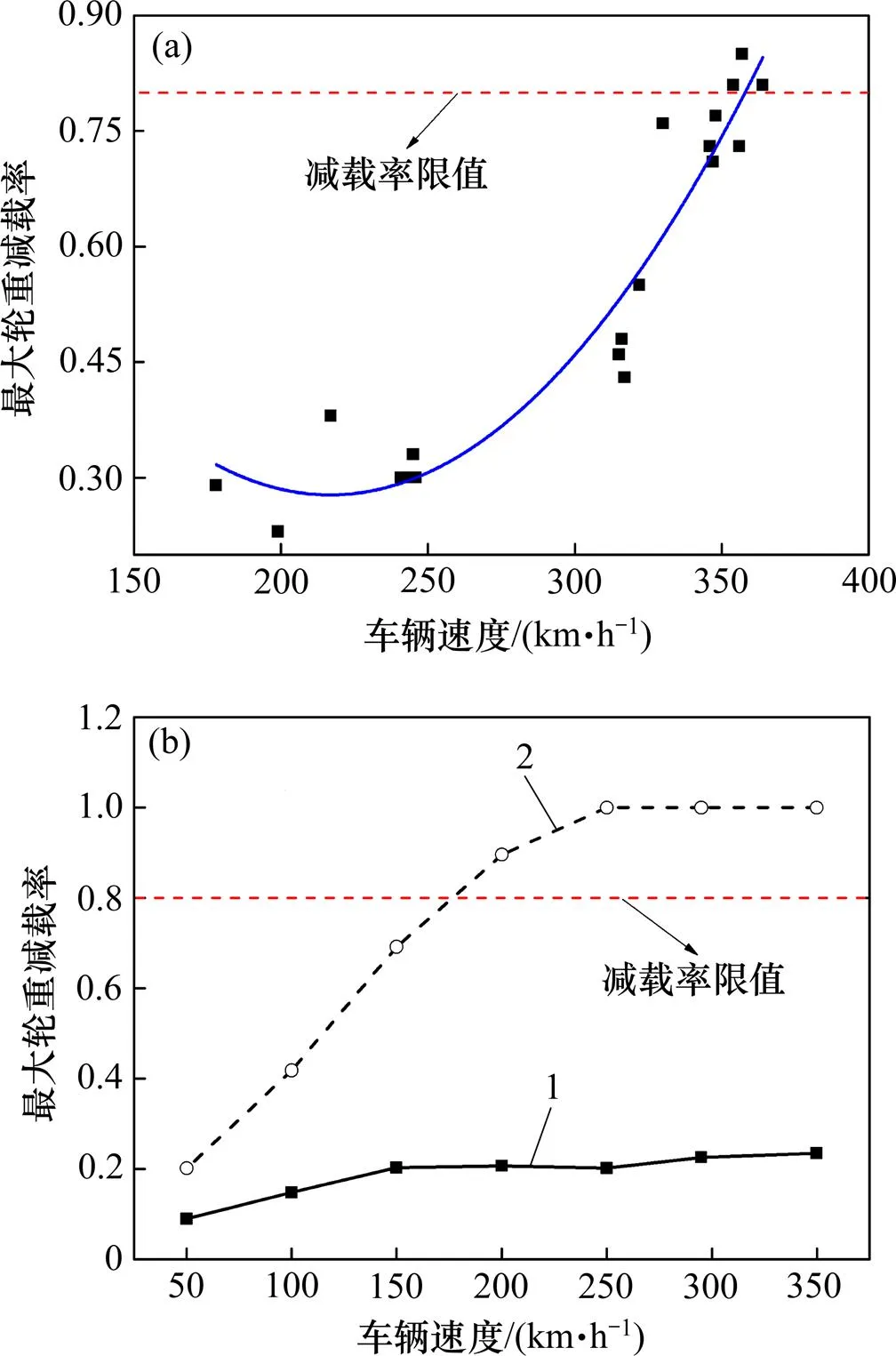
(a) 现场实测;(b) 仿真计算
由图10(b)可以看出:当岔区钢轨存在轧制不平顺时,最大轮重减载率随着列车速度的增高而显著增大,若要保证轮重减载率不超过0.8的限值,理论上列车过岔时应限速为160 km/h;而当钢轨不存在轧制不平顺时,最大轮重减载率随列车速度的增高其增幅较小。动力学仿真分析结果较地面测试结果略大,主要是由于地面测试时测点布置较少且未在最不利位置布点。
以上道岔动力学仿真分析的结果表明:钢轨轧制不平顺导致钢轨本身存在垂直不平顺,正是由于道岔钢轨本身的垂直不平顺造成了动车组车辆高速通过道岔时的轮重减载率超限,为解决此类问题,可通过改进钢轨矫直生产工艺消除钢轨轧制不平顺,现场可通过钢轨打磨消除轧制不平顺的影响或更换现场已铺设的、超过平直度标准的钢轨。
4 结论
1) 由于高速铁路钢轨复合矫直工艺控制精度的不足,容易使钢轨在矫直过程中产生轧制周期性不平顺,该不平顺的主频波长为0.8 m的整倍数。
2) 动车组车辆以350 km/h的速度直向通过存在钢轨轧制不平顺的18号高速道岔时,两侧垂向轮轨力变化较为剧烈,且直基本轨侧由于钢轨轧制不平顺的存在,有多处轮轨对应接触位置出现车轮悬空状态;直基本轨侧垂向轮轨力的一阶主频为50.51 Hz,道岔全线轨道不平顺的一阶主频波长为1.9 m,动车组车辆速度为350 km/h,换算为一阶主频为51.17 Hz,两者的一阶主频近似相等。
3) 动车组车辆通过道岔时,波长较短的轨道不平顺相比波长较长的轨道不平顺更容易引起轮重减载率超限。岔区钢轨存在轧制不平顺时,最大轮重减载率随着列车速度的增高而显著增大,若要保证轮重减载率不超过0.8的限值,理论上列车过岔时应限速为160 km/h;而当钢轨不存在轧制不平顺时,最大轮重减载率随列车速度的增高其增幅较小。
4) 高速铁路钢轨由于矫直工艺产生的轧制不平顺会导致钢轨本身存在垂直不平顺,正是由于道岔钢轨本身的垂直不平顺会造成动车组车辆高速通过道岔时轮重减载率超限,为解决此类问题,可通过改进钢轨矫直生产工艺消除钢轨轧制不平顺,现场可通过钢轨打磨消除轧制不平顺的影响或更换现场已铺设的、超过平直度标准的钢轨。
[1] 熊卫东, 周清跃, 穆恩生. 高速铁路钢轨的平顺性[J]. 中国铁道科学, 2000, 21(3): 76−83.XIONG Weidong, ZHOU Qingyue, MU Ensheng. The smoothness of high-speed railway track rails[J]. China Railway Science, 2000, 21(3): 76−83.
[2] WANG Ping. Design of high-speed railway turnouts (theory and applications)[M]. Amsterdam: Elsevier Academic Press, 2015: 86−87.
[3] 周永健, 练松良, 杨文忠. 轨面短波不平顺对轮轨力影响的研究[J]. 华东交通大学学报, 2009, 26(4): 6−12. ZHOU Yongjian, LIAN Songliang, YANG Wenzhong. Research of impact of short wave track irregularity on the wheel-rail force[J]. Journal of East China Jiaotong University, 2009, 26(4): 6−12.
[4] 徐庆元, 曹扬风, 周小林. 短波随机不平顺对列车−板式无砟轨道−路基系统振动特性的影响[J]. 中南大学学报(自然科学版), 2011, 42(4): 1105−1110. XU Qingyuan, CAO Yangfeng, ZHOU Xiaolin. Influence of short wave random irregularity on vibration characteristic of train−slab track−subgrade system[J]. Journal of Central South University (Science and Technology), 2011, 42(4): 1105−1110.
[5] 徐磊, 陈宪麦, 李晓健, 等. 朔黄重载铁路轨道不平顺谱分析[J]. 中南大学学报(自然科学版), 2013, 44(12): 5149−5153. XU Lei, CHEN Xianmai, LI Xiaojian, et al. Track irregularity spectrum analysis of Shenchi—Huanghua heavy haul railway[J]. Journal of Central South University (Science and Technology), 2013, 44(12): 5149−5153.
[6] 陈宪麦, 徐磊, 徐伟昌, 等. 高速铁路(京沪、沪宁、沪杭线)轨道不平顺谱分析[J]. 铁道科学与工程学报, 2013, 10(4): 1−6. CHEN Xianmai, XU Lei, XU Weichang, et al. Analysis of track irregularity spectrum for high-speed railway (Beijing—Shanghai, Shanghai—Ningbo and Shanghai—Hangzhou railway)[J]. Journal of Railway Science and Engineering. 2013, 10(4): 1−6.
[7] 徐庆元. 短波随机不平顺对列车−板式无砟轨道−桥梁系统动力特性影响[J]. 土木工程学报, 2011, 44(10): 132−137. XU Qingyuan. Influence of short-wave random irregularity on the dynamic characteristics of train−slab track−bridge system[J]. China Civil Engineering Journal. 2011, 44(10): 132−137.
[8] SEMIH S, ALI E A. Dynamic modeling and fuzzy logic control of vibrations of a railway vehicle for different track irregularities[J]. Simulation Modeling Practice and Theory. 2011, 19(9): 1873−1894.
[9] 郭然, 韩宝明, 李得伟, 等. 具有更新机制的铁路轨道不平顺灰色预测模型[J]. 中南大学学报(自然科学版), 2013, 44(10): 4334−4341. GUO Ran, HAN Baoming, LI Dewei, et al. Grey prediction model for track irregularity with update mechanism[J]. Journal of Central South University (Science and Technology), 2013, 44(10): 4334−4341.
[10] 陈嵘, 李帅, 王源, 等. 基于轨道局部波动的高速铁路轨道平顺状态评估方法[J]. 铁道学报, 2017, 39(2): 105−111. CHEN Rong, LI Shuai, WANG Yuan, et al. Evolution method of rail regularity state based on track local fluctuation in high-speed railway[J]. Journal of the China Railway Society, 2017, 39(2): 105−111.
[11] 程佩青. 数字信号处理教程[M]. 北京: 清华大学出版社, 2011: 143−144. CHENG Peiqing. Digital signal processing tutorial[M]. Beijing: Tsinghua University Press, 2011: 143−144.
[12] 吴大正. 信号与线性系统分析[M]. 北京: 高等教育出版社, 2005: 134−142. WU Dazheng. Signal and linear system analysis[M]. Beijing: Higher Education Press, 2005: 134−142.
[13] 陈春俊, 李华超. 频域采样三角级数法模拟轨道不平顺信号[J]. 铁道学报, 2006, 28(3): 38−42. CHEN Chunjun, LI Huachao. Track irregularity simulation in frequency domain sampling[J]. Journal of the China Railway Society, 2006, 28(3): 38−42.
[14] 曹阳. 道岔平面线型动力分析及其设计方法研究[D]. 成都: 西南交通大学土木工程学院, 2013: 33−64. CAO Yang. Studt on dynamic analysis and design methods of the turnout layout geometry[D]. Chengdu: Southwest Jiaotong University. School of Civil Engineering, 2013: 33−64.
[15] 金新灿, 孙守光, 陈光雄. 车辆通过道岔时转向架结构系统振动特性研究[J]. 工程力学, 2007, 24(1): 178−185. JIN Xincan, SUN Shougaung, CHEN Guangxiong. Study on vibrational characteristics of railway bogie when rolling-stock running through a switch[J]. Engineering Mechanics, 2007, 24(1): 178−185.
[16] 任尊松, 孙守光. 道岔区轮轨接触几何关系研究[J]. 工程力学, 2008, 25(11): 223−230. REN Zunsong, SUN Shouguang. Study on the wheel/rail contact geometry relation of the turnout zone[J]. Engineering Mechanics, 2008, 25(11): 223−230.
[17] 马晓川, 王平, 王健, 等. 尖轨降低值超限对转辙器动力特性的影响研究[J]. 铁道学报, 2016, 38(3): 98−105. MA Xiaochuan, WANG Ping, WANG Jian, et al. Study on impact of over-limit reduced value of switch rail on dynamic characteristics of switch[J]. Journal of the China Railway Society, 2016, 38(3): 95−105.
[18] WANG Ping, MA Xiaochuan, WANG Jian, et al. Optimization of rail profiles to improve vehicle running stability in switch panel of high-speed railway turnouts[J]. Mathematical Problems in Engineering, 2017, 2017: 1-13.
[19] 全顺喜. 高速道岔几何不平顺动力分析及其控制方法研究[D]. 成都: 西南交通大学土木工程学院, 2012: 37−39. QUAN Shunxi. Study on dynamic analysis and control methods of the geometric irregularity in high-speed turnout[D]. Chengdu: Southwest Jiaotong University. School of Civil Engineering, 2012: 37−39.
[20] 陈果. 车辆−轨道耦合系统随机振动分析[D]. 成都: 西南交通大学列车与线路研究所, 2000: 100−104. CHEN Guo. The analysis on random vibration of vehicle-track coupling system[D]. Chengdu: Southwest Jiaotong University. Train & Track Research Institute, 2000: 100−104.
(编辑 杨幼平)
Effect of rail straightening irregularity on vertical dynamic characteristics of vehicle-turnout coupling system
MA Xiaochuan, WANG Ping, XU Jinhui, XU Jingmang, CHEN Rong
(MOE Key Laboratory of High-speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031, China)
In order to analyze the cause of track irregularity in a No.18 high speed turnout, the frequency distribution was calculated by the method of Fast Fourier Transform, and the track irregularities of switch and frog section were caused by the accuracy of rail straightening operation, and the wavelength of dominate frequency was a multiple of 0.8 m. A model was established based on the vehicle-turnout coupling system dynamic theory which was used to analyze the effect of straightening irregularity on vertical wheel-rail force and reduction rate of wheel load, in addition, the effect of vehicle velocity on the maximum reduction rate of wheel load is analyzed by the model. The results indicate that the vertical wheel-rail force has a drastic change when the vehicle passes the high-speed turnout at a velocity of 350 km/h. The first dominate frequency of vertical wheel-rail force is 50.51 Hz and the first dominate frequency of the track irregularity is 51.27 Hz, and the former is approximately equal to the later. The maximum reduction rate of wheel load at frog is above standard of 0.8, and it is likely to derail when the time of duration is longer. The maximum reduction rate of wheel load is significantly affected by the increase of vehicle velocity when there is rail irregularity in the turnout. The vehicle velocity should be limited to 160 km/h to ensure the reduction rate of wheel load at the limit value of 0.8 theoretically, the vehicle velocity has a little impact on the maximum reduction rate of wheel load when the track has no straightening irregularity.
vehicle; turnout; rail straightening irregularity; vertical wheel-rail force; reduction rate of wheel load
10.11817/j.issn.1672-7207.2017.07.035
U213.6
A
1672−7207(2017)07−1942−09
2016−07−08;
2016−10−12
国家自然科学基金资助项目(51378439,51425804,U1334203,U1234201);西南交通大学优秀博士学位论文资助项目(2015) (Projects(51378439, 51425804, U1334203, U1234201) supported by the National Natural Science Foundation of China; Project(2015) supported by the Doctoral Dissertation Cultivation Project of Southwest Jiaotong University)
徐井芒,博士,讲师,从事铁路道岔轨道结构及轨道动力学研究;E-mail: mang0800887@163.com

