某些近于凸函数的子族的一些性质
傅秀莲
(广东工贸职业技术学院 计算机系, 广州 510510)
某些近于凸函数的子族的一些性质
傅秀莲
(广东工贸职业技术学院 计算机系, 广州 510510)
本文介绍和研究了一个近于凸函数的子族Ks(λ,α,β)的问题. 得到了包含关系,系数不等式和卷积等性质,推广了Ks(α,β)结果.
近于凸函数; 卷积; 系数估计
用A表示在U={z:z∈C,|z|<1}上形如
的全体解析函数所成的函数类.用S表示在A中全体单叶函数族.


设f(z)和F(z)在U内解析,如果存在U内的解析函数w(z)使得|w(z)|≤|z|且满足f(z)≡F(w(z)),则称f(z)从属于F(z),记为f(z)F(z)或者fF.若f(z)在U内单叶,则f(z)F(z)当且仅当f(0)=F(0)和f(U)⊂F(U).



本文模仿C(k)(λ,α,β)的定义,给出了函数族Ks(λ,α,β)的定义,定义如下:
定义1 设0≤α≤1,0<β≤1,0≤λ≤1,如果函数f(z)∈A满足

特别地,Ks(0,α,β)=Ks(α,β),所以Ks(λ,α,β)是Ks(α,β)的推广.
为了得到定理,需要下面的几个引理.


其中
B2n-1=2b2n-1-2b2b2n-2+…+
则G(z)∈S*.





主要结论:
定理1 设0≤α≤1,0<β≤1,0≤γ≤1,则f∈Ks(λ,α,β)当且仅当



则式(2)可以写成


定理2 设0≤α≤1,0<β≤1,0≤λ≤1,则Ks(λ,α,β)⊂C⊂S.
下面分两种情况讨论:
1)当λ=0,显然f(z)=F(z)∈C.

定理3 设0≤α1≤α2≤1,0<β1≤β2≤1,0≤λ≤1.则Ks(λ,α1,β1)⊂Ks(λ,α2,β2).
证明:设f(z)∈Ks(λ,α1,β1),由定理1可得




其中B2n-1由式(4)给出.
证明:令F(z)=(1-λ)f(z)+λzf′(z),通过计算可得

所以F(z)和G(z)满足引理5的条件,由式(5)可得式(7).

成立,其中B2n-1由式(4)给出,则f∈Ks(λ,α,β).
证明:令F(z)=(1-λ)f(z)+λzf′(z),通过计算可得

则对于z∈U,有
M=|zF′(z)-G(z)|-β|αzF′(z)+G(z)|=

取|z|=r<1,有

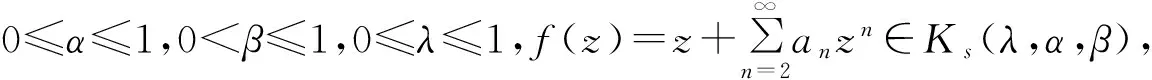
(9)
其中[]表示高斯符号.
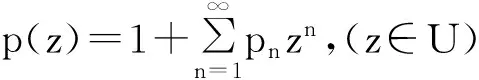

由引理6有
另一方面,由引理7有
把f(z),G(z)和p(z)的表达式代入式(10),得到
(1+p1z+p2z2+p3z3+…+pnzn+…)
(z+B3z3+…+B2n-1z2n-1+…)=
z+2(1+λ)a2z2+…+2n(1+(2n-1)λ)a2nz2n+
从式(13)可得
2n(1+(2n-1)λ)a2n=p1B2n-1+p3B2n-3+
(2n+1)(1+2nλ)a2n+1=B2n+1+p2B2n-1+
结合式(11),(12),(14)和(15)可以得到
由式(16)和(17)可得式(9).证毕.
定理7 令|ξ|=1.则f(z)∈Ks(λ,α,β)当且仅当
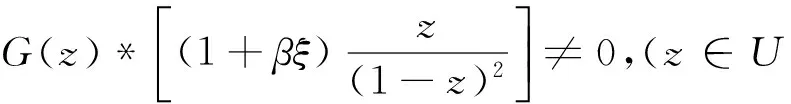
其中G(z)由式(3)给出.
证明:设f(z)∈Ks(λ,α,β),由定理1可得

这等价于
式(19)可以写成


注意到
把式(21)和(22)代入式(20),可以得到式(18).证毕.
[1] Gao C, Zhou S. On a Class of Analytic Functions Related to the Starlike Functions[J]. Kyungpook Math. J. 2005,45(1):123-130.
[2] Wang Z G, Gao C Y, Yuan S M. On Certain Subclass of Close-to-convex Functions[J]. Acta Mathematica Academiae Paedagogicae Nyíregyháziensis, 2006, 22(3):171-177.
[3] Wang Z G, Gao C Y, Liu M S, et al. On Subclasses of Close-to-convex and Quasi-convex Functions with Respect to k-symmetric Points[J]. Advances in mathematics, 2009,38(1):44-56.
[4] Wang Z G, Jiang Y P. On Certain Subclasses of Convex-to-convex and Quasi-convex Functions with Respect to 2k-symmetric Conjugate Points[J]. J. Math. Appl.,2007,29:167-179.
[5] Wang Z G, Gao C Y, Yuan S M. On Certain Subclasses of Close-to-convex and Quasi-convex Functions with Respect to k-symmetric Points[J]. J. Math. Anal. Appl.,2006,322(1):97-106.
[6] Kamali M, Akbulut S. On a Subclass of Certain Convex Functions with Negative Coefficients[J]. Appl. Math. Comput., 2003,145(2):341-350.
[7] Sudharsan T V, Balasubrahmanyam P, Subramanian K G. On Functions Starlike with Respect to Symmetric and Conjugate Points[J]. Taiwanese J.Math.,1998, 2(1):57-68.
[8] W. Rogosinski. On the Coefcients of Subordinate Functions[J]. Proc. London Math. Soc., 1945,48(1):48-82.
[责任编辑 王迎春]
Some Properties of Certain Subclass of Close-to-Conves Functions
Fu Xiulian
(Department of Computer Science, Guangdong College of Industry and Commerce, Guangzhou 510510, China)
A certain new subclassKs(λ,α,β) of close-to-convex functions is introduced and discussed. The results such as inclusion relationships,coefficient inequalities and convolution property are derived, so as to generalize the results of the subclassKs(α,β).
close-to-convex functions; convolution; coefficient bounds
2016-12-05
广东省自然科学基金自由申请项目“随机Laplace-Stieltjes变换的值分布与复方程解的存在性”(2015A030313628)
傅秀莲(1979-),女,硕士,副教授,主要研究方向为复分析及其应用.E-mail: xxfxl@163.com
10.13393/j.cnki.issn.1672-948X.2017.04.022
O174.51
A
1672-948X(2017)04-0106-04

