蛾群算法与投影寻踪耦合模型在区域水资源脆弱性评价中的应用
崔东文
(云南省文山州水务局, 云南 文山 663000)
蛾群算法与投影寻踪耦合模型在区域水资源脆弱性评价中的应用
崔东文
(云南省文山州水务局, 云南 文山 663000)
提出一种新型群智能算法——蛾群算法(MSA)与投影寻踪(PP)技术耦合的水资源脆弱性评价模型,以云南省16个州市水资源脆弱性评价为例进行研究.从水量、水质、洪灾和旱灾4个方面遴选28个指标构建区域水资源脆弱性评价指标体系和分级标准;通过8个典型测试函数对MSA进行仿真验证,并与差分进化(DE)算法、文化算法(CA)、教学优化(TLBO)算法和粒子群优化(PSO)算法的仿真结果进行对比.利用MSA、DE、CA、TLBO和PSO算法优化PP最佳投影方向,构建MSA-PP、DE-PP、CA-PP、TLBO-PP和PSO-PP耦合模型对实例水资源脆弱性进行评价.结果表明:MSA寻优精度优于DE等4种算法,具有较好的全局极值寻优能力和收敛稳定性能,在求解高维、复杂优化问题时有着更高的求解精度;MSA-PP模型对昆明、玉溪、曲靖、楚雄4州市的水资源脆弱性评价为”轻度脆弱“,对怒江州、迪庆州评价为“重度脆弱”,其余州市评价为“中度脆弱”.MSA-PP模型对实例评价结果与TLBO-PP模型相同,但在排序上存在差异;与CA-PP、DE-PP和PSO-PP模型的评价结果及排序上均存在差异,表明智能算法求解精度的高低决定了评价效果的优劣.本文提出的模型及验证方法具有通用性,可推广应用于其他领域.
水资源脆弱性评价; 指标体系; 分级标准; 投影寻踪; 蛾群算法; 仿真验证
水资源脆弱性研究较早,始于20世纪60年代,由于学术界对脆弱性的定义不统一,从而导致了水资源脆弱性在内涵上的理解不尽相同.普遍认同的水资源脆弱性是指在自然环境因素和经济社会因素的双重影响下,水资源系统正常的结构和功能受到损坏并难以恢复到原有状态的倾向或趋势[1-4].开展水资源脆弱性评价对于量化区域水资源脆弱性程度、反映区域水资源安全、提高水资源系统决策适应能力具有重要意义.但也存在几方面的问题:1)虽然水资源脆弱性概念提出时间较早,但目前尚未形成科学、系统的理论体系及普遍认同的评价指标与分级标准.2)采用层次分析法[5]、专家意见法[6]、模糊层次分析法[7]等方法确定指标权重存在主观臆断成分较大的缺陷;采用主成分-因子分析法[8]降维易造成指标信息量丢失等不足.3)水资源脆弱性评价涉及水资源、水环境、经济社会等领域,属多指标、高维、非线性系统问题,在不降维情况下,上述等方法难以处理超过20维的复杂系统评价问题.投影寻踪(Projection Pursuit,PP)技术是将高维数据投影到低维空间,并在低维空间进行数据分析研究的统计方法,在克服维数祸根、解决超高维等问题中具有明显优势.对于PP技术,最佳投影方向是决定其评价或计算精度的关键.目前,除遗传算法[9](Genetic Algorithm,GA)被广泛用于PP技术最佳投影方向的选取外,粒子群优化(Particle Swarm Optimization,PSO)算法[10]、差分进化(Differential Evolution,DE)算法[11]、萤火虫算法(Firefly Algorithm,FA)[12]以及近年才被提出的仿生群智能算法如群居蜘蛛优化(Social Spider Optimization,SSO)算法[13]、鸡群优化(Chicken Swarm Optimization,CSO)算法[14]等被尝试用于PP技术最佳投影方向的选取,并取得了较好的优化选取效果.蛾群算法(Moth Swarm Algorithm,MSA)是文献[15]于2016年提出的一种新型仿生群体智能算法,该算法灵感源自于飞蛾始终朝向月光方向.除飞蛾火焰优化(Moth-Flame Optimization,MFO)算法[16-17]提出的自适应高斯步进、螺旋飞行外,该算法通过Lévy飞行即时记忆、群体多样性交叉关联学习机制提升了MSA的开发和探索能力.从算法灵感来源、优化机制来看,MSA可以认为是MFO算法的改进,具有较好的全局极值寻优能力和收敛稳定性能.
本文结合PP技术及MSA优点,建立MSA与PP耦合的水资源脆弱性评价模型,对云南省16个州市水资源脆弱性进行评价分析.主要步骤为:1)从水量、水质、洪灾和旱灾4个方面遴选28个指标构建区域水资源脆弱性评价指标体系和分级标准.2)采用8个典型测试函数对MSA进行仿真验证,并与DE、文化算法(Cultural Algorithm,CA)、教学优化(Teaching-Learning-Based Optimization,TLBO)算法和PSO算法的仿真结果进行对比分析.3)利用MSA、DE、CA、TLBO和PSO算法优化PP最佳投影方向,构建MSA-PP、DE-PP、CA-PP、TLBO-PP和PSO-PP耦合模型对云南省16个州市水资源脆弱性进行评价分析.
1 评价指标体系及分级标准
脆弱性概念源于灾害脆弱性,其与不同的研究对象结合,便产生了不同的研究分支.水资源脆弱性涵盖了水资源、水环境、水旱灾害及社会经济等领域,属非线性、高维、复杂系统问题.目前,虽然国内外学者从不同的关注点开展了水资源脆弱性评价研究[1-8,18],但尚未形成普遍认同的指标体系、分级标准以及成熟的评价方法.
笔者参考相关文献[3-4,18],并结合区域实际,遵行科学性、可量化、可操作、指标可获取等原则,从水量、水质、洪涝灾害和旱灾4个方面遴选出28个指标构建具有目标层A、准则层B和指标层C的区域水资源脆弱性评价指标体系及“不脆弱(Ⅰ)”、“轻度脆弱(Ⅱ)”、“中度脆弱(Ⅲ)”、“重度脆弱(Ⅳ)”、“极度脆弱(Ⅵ)”5个等级的分级标准,见表1.

表1 区域水资源脆弱性评价指标体系及分级标准
注:“+”表示正向指标,指标越大,其脆弱性越弱;“-”表示负向指标,指标越大,其脆弱性越强.
2 MSA-PP水资源脆弱性评价模型
2.1 PP技术
PP技术用于水资源脆弱性评价的简要算法如下[13-14]:
Step1:数据预处理.设样本评价指标集为{x(i,j)|i=1,2,…,n;j=1,2,…,m},对于正向指标利用式(1)进行处理;负向指标取倒后乘100后再利用式(1)进行数据处理.
式中,x(i,j)为指标特征值归一化序列;xmax(i,j)、xmin(i,j)分别为第j个指标值的最大和最小值;n、m分别为样本容量和指标数目.
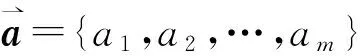

Step3:优化投影指标函数.将搜寻最优投影方向问题转化为非线性最优求解问题,即
式中,Sz为投影值z(i)的标准差;Dz为投影值z(i)的局部密度.Sz、Dz表达式参见文献[12,16].

2.2 MSA数学描述
设待优化问题的可行解和适应度函数值分别由光源位置和光源发光强度表示,依据文献[15],MSA蛾群由3组蛾群组成:1)勘探蛾:能够在优化空间上发现新的区域,具有先进先出的一小组飞蛾(np).这组蛾群的主要任务是将辨别的最佳位置作为光源引导主群的运动(光路);2)探测蛾:在光源附近区域内漫游到随机螺旋路径中一组已被勘探蛾标识的蛾群;3)观察蛾:一组由探测蛾获得并直接向最佳全局解漂游的蛾群;4)在每次迭代过程中,蛾群中最好适应度值被认为是勘探蛾空间位置所对应的发光强度,勘探蛾领导下一次更新迭代;第二、第三好的适应度值分别定义为探测蛾和观察蛾.
MSA数学模型描述如下[15]:1)初始化.对于蛾群规模为n的d维优化问题,采用下式随机创建初始候选解位置,并基于适应度函数值将蛾群分为勘探蛾、探测蛾和观察蛾.
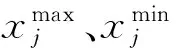
2)侦察阶段.为了消除早熟及趋同现象,采用以下步骤来提升MSA的开发和探索能力:


变异系数μt,即相对分散度可以如下表示:
任何勘探蛾的组成都会受到低分散度的影响,即勘探蛾数量在交叉点cp中被确认.
可以看出,交叉点随着所提出的策略变化而动态地改变.
b.Lévy飞行.Lévy飞行数学描述如下:
Li~step⊕Lé
式中,Γ(x)=(x-1)!.
c. 差异向量Lévy突变.对于nc∈cp,利用下式突变策略合成子跟踪向量
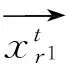
式中,Lp1、Lp2为两个独立的相同变量,即突变缩放因子,由Lévy飞行随机生成;相互索引集合(r1,r2,r3,r4,r5,p)来自于勘探蛾群候选解.
d. 自适应交叉操作.为了获得全局最优解,勘探蛾个体通过子跟踪向量交叉操作更新其位置.描述如下:
e. 选择策略.利用适应度函数值选择下一次迭代操作:
概率值Pp与发光强度fitp成比例,计算如下:
基于发光强度的最小值化问题目标函数值fitp由下式公式计算:
3)横向定向.MSA通过将锥形顶点保持在固定角度,将蛾群朝向光源的飞行路径描述为围绕锥体表面的一组轨迹,将具有次发光强度的蛾群定义为探测蛾,并利用下式在迭代过程中自适应地减少探测蛾数量.
探测蛾个体xi根据下式螺旋飞行路径更新其位置.其可以数学表达如下:

式中,θ∈[r,1]为用于定义螺旋形状的随机数,其中,和r=-1-t/T.
在MSA模型中,每种飞蛾类型是动态变化的.任何探测蛾发现比当前位置更佳的光源位置,探测蛾将被替换为勘探蛾.
4)天体导航.在优化过程中,探测蛾数量的减少将导致观察蛾数量的增加,这可能导致MSA早熟收敛.蛾群中具有最低发光强度的蛾被认为是观察蛾,这些蛾群旨在直接向最佳全局解漂游.在这一阶段,MSA通过两个策略来提升观察蛾的搜索性能.
a. 高斯游走.新观察蛾利用下式进行高斯随机游走,描述如下:
;

ε1~random(size(d))⊕
式中,ε1是从高斯随机分布抽取的随机样本缩放到该组的大小;bestg是从勘探蛾和探测蛾中获得的全局最优解,ε2和ε3是区间[0,1]内均匀分布的随机数.
b. 具有即时记忆的关联学习机制.在现实世界中,飞蛾因没有记忆功能而易陷入火焰中.因此,MSA提出了具有联想学习和短期记忆的观察蛾群,其联想学习和短期记忆功能在观察蛾个体之间起到交流和信息共享作用.观察蛾位置更新方程可表示如下:
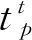
式中,i∈{1,2,…,nA};2t/T为社会因子;1-t/T为认知因子;r1、r2为[0,1]区间内的随机数;bestp是基于新勘探蛾对应概率值中随机选择的当前最优解.
2.3 MSA-PP脆弱性评价实现步骤
MSA-PP水资源脆弱性评价步骤可归纳如下[13-15]:
Step1:构建水资源脆弱性评价指标体系和分级标准,利用式(1)对各州市脆弱性评价指标及5个等级的分级阈值进行一致性处理.
Step2:确定目标函数.选取式(3)作为MSA等5种算法优化的目标函数,即适应度函数.
Step3:设置算法参数.设置最大迭代次数T、飞蛾种群规模n、搜索空间维数d以及勘探蛾数量np,令当前迭代次数t=1.
Step4:算法初始化.利用式(4)随机创建第i只飞蛾第j维空间中的初始位置xij.
Step5:利用式(3)计算适应度函数值,并基于适应度值将蛾群分为勘探蛾、探测蛾和观察蛾.

Step7:利用式(11)进行种群多样性自适应交叉操作;基于适应度函数值,利用式(12)~式(14)选择下一次迭代操作方式.
Step8:利用式(15)定义探测蛾减少数量nf;利用式(16)更新第t+1次迭代探测蛾个体xi的新位置,并计算探测蛾个体适应度值,确定新光源和月光位置.
Step9:对于观察蛾个体,如果i∈nG,利用式(17)~式(18)进行高斯随机游走更新观察蛾个体的空间位置;如果i∉nG,利用式(19)更新具有即时记忆关联学习机制的观察蛾个体空间位置.
Step10:计算观察蛾个体适应度函数值,并利用适应度函数值确定新光源位置、月光位置,以及蛾群类型(勘探蛾、探测蛾和观察蛾).
Step11:判断算法迭代终止条件是否满足,若满足则转至Step10,否则令t=t+1,并执行Step6~Step11.
Step12:输出最优蛾群个体值和全局极值,即月光所处的空间位置和最强光源发光强度,算法结束.

3 仿真验证与结果分析
为了检验MSA寻优性能,选取8个标准测试函数进行仿真实验,见表2.仿真结果与TLBO、DE、CA和PSO 4种算法的仿真测试结果进行比较,见表3.其中,f1~f5为单峰函数,用于测试算法的收敛速度和寻优精度;f6~f8为多峰函数,用于测试算法跳出局部极值及全局搜索能力.
实验参数设置如下:MSA最大迭代次数T=1 000,种群规模n=50,勘探蛾数量np=5.TLBO算法最大迭代次数T=1 000,群体规模n=50,TF为1~10之间随机整数.DE算法最大迭代次数T=1 000,种群规模n=50,上下限的尺度因子分别为0.8、0.2,交叉率CR=0.2.CA最大迭代次数T=1 000,群体规模n=50,根据标准知识产生的群体规模n′=50.PSO算法最大迭代次数T=1 000,种群规模n=50,ω=0.729,局部学习因子、全局学习因子c1=c2=2.0.

表2 基准函数

表3 函数优化对比结果
5种算法基于Matlab 2010a用M语言实现,分别对表2中8个测试函数独立运行20次,记录5种算法的平均值和标准差,比较结果见表3.
1)从表3的比较结果可知,对于单峰函数f1~f5,除Step函数(f5)外,MSA寻优获得的平均值高于TLBO、DE、CA和PSO 4算法100个数量级以上,表现出更好的求解精度和全局极值寻优能力,尤其是Sphere函数(f1)和Schwefel1.2函数(f3),MSA均能收敛到理论最优值0.对于多峰函数f6~f8,MSA寻优精度均优于TLBO、DE、CA和PSO,尤其是Griewank函数(f5)和Rastrigin(f6),MSA均能收敛到理论最优值0,表现出较好的新区域搜索能力、极值寻优能力和跳出局部极值能力.
2)对于标准差,除Step函数(f5)和Ackley函数(f8)外,MSA寻优获得的标准差均为0,表现出较高的算法的收敛稳定性.其中,MSA对于Ackley函数(f8)寻优获得的标准差高于其他4种算法15个数量级以上.
3)从8个函数寻优效果整体比较而言,优化性能从优至劣依次是:MSA、TLBO、DE、CA、PSO.
结果比较表明,无论是单峰还是多峰函数,基于Lévy飞行即时记忆、群体多样性交叉关联学习机制的MSA具有较好的开发和探索能力,在求解高维、复杂优化问题时具有更好的求解精度和全局极值寻优性能.
4 实例应用
4.1 研究区概况
云南省地处祖国西南边陲,辖昆明、曲靖、玉溪等16个州市.境内河流分属长江、珠江、红河、澜沧江、怒江、伊洛瓦底江6大水系.多年平均降水量1 278.8 mm,自产水资源总量2 210亿m3,从邻近省区入境水量1 625亿m3,从缅甸、越南、老挝入境水量25亿m3,出境水量3 835亿m3,多年平均地下水资源量767亿m3,水资源总量相对丰富.近年来,随着云南省工业化、城镇化快速推进和全球气候变化影响加剧,云南省水资源脆弱性日益突出.本文以2014年云南省16个州市水资源脆弱性评价为研究对象,指标数据来源于《2014年云南省水资源公报》、《2014年云南省统计年鉴》、《2014年云南省水利年鉴》等.
4.2 水资源脆弱性评价模型求解
1)模型求解.依据MSA-PP水资源脆弱性评价
模型求解步骤,采用式(1)对各州市评价指标进行一致性处理,利用处理后的指标数据构造投影目标函数,并运用MSA、DE、TLBO、CA和PSO算法优化式(3),求解PP模型最佳投影方向(5种算法搜索空间设置为[-1,1],维度为28维,其余参数设置均同上).将5种算法连续运行20次,求解最优适应度值的平均值、标准差和最佳投影方向的平均值,见表4.
2)投影值计算及评价.利用表4最佳投影方向(20次均值)计算水资源脆弱性评价等级标准(见表5)和各州市综合投影值;利用等级标准对各州市水资源脆弱性进行评价,其评价及排序结果见表6.
3)进化过程图绘制.5种算法某次进化过程见图1(为了便于观察,图1为在纵坐标轴[4070 4087]上的截图).
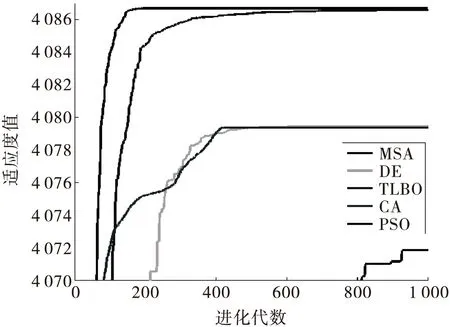
图1 5种算法某次优化进化过程图

算法平均值标准差投影方向(20次均值)MSA4086.69638.01×10-5(0.27480.05450.22040.26200.20050.25480.20610.06120.21010.20550.2693-0.0733-0.01210.07260.03830.09940.27060.2458-0.01630.27250.2662-0.00520.28160.1809-0.00820.17420.22120.0612)TLBO4084.07121.1146(0.27960.04360.21290.25450.20240.25750.19420.03820.20250.20420.2633-0.0914-0.03330.04540.01740.09680.27250.2448-0.03690.27910.2716-0.00350.28170.1678-0.01170.16210.22550.0382)DE4082.83831.7808(0.26540.06730.22230.26520.24790.26060.22510.06660.22910.20610.2654-0.0722-0.01040.07050.05090.10480.26540.2585-0.01890.26530.2654-0.00320.18000.1973-0.00520.16730.22950.0666)CA4064.184015.8956(0.26380.06030.20430.26480.19040.24720.20880.07040.23770.26340.3076-0.05950.00730.13130.08260.09610.25620.24760.00920.25670.2650-0.06920.27300.14960.00080.18300.10910.0704)PSO4008.226127.5735(0.22400.03720.19540.23040.14400.26680.20790.10940.17760.21780.2298-0.0258-0.0317-0.03960.02580.09720.14470.2022-0.02180.21850.26410.02500.23400.2014-0.02900.19850.24450.1094)

表5 水资源脆弱性评价等级划分结果
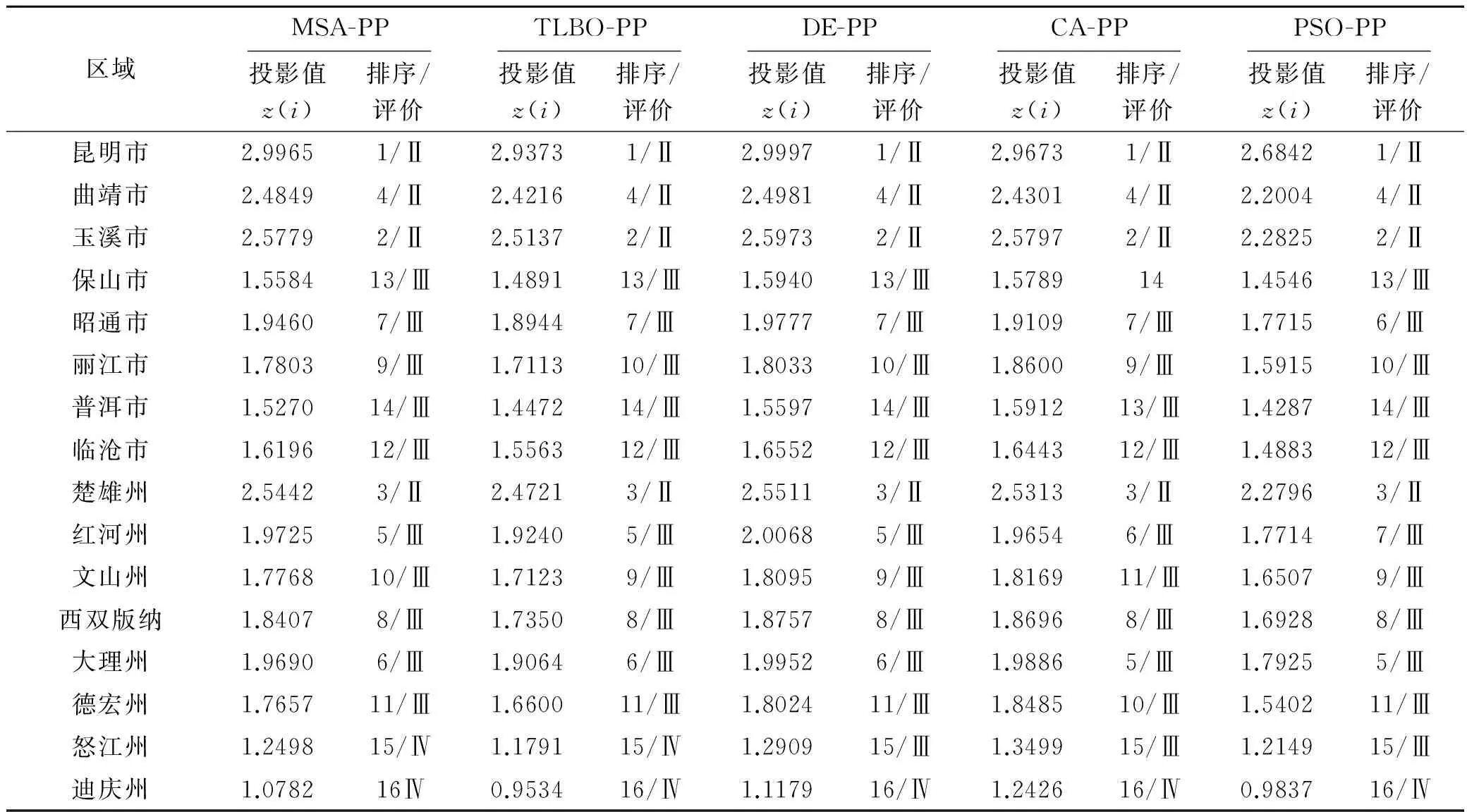
表6 各州市水资源脆弱性投影值及排序评价结果
4.3 评价结果分析
从表4~表6及图1可以得到以下结论:
1)从表4及图1来看,MSA优化目标函数式(3)获得的平均值、标准差均优于TLBO、DE、CA和PSO算法,其中,标准差高于其他4种算法4个数量级以上.再次验证了MSA具有较好的求解精度、极值寻优能力和算法稳定性能.

3)从表6来看,MSA-PP模型对昆明、玉溪、曲靖、楚雄4州市的水资源脆弱性评价为“轻度脆弱”,对怒江州、迪庆州评价为“重度脆弱”,其余州市评价为“中度脆弱”.MSA-PP模型对实例评价结果与TLBO-PP模型相同,但在排序上存在差异;与DE-PP、CA-PP和PSO-PP模型的评价结果及排序上均存在差异;其中,与CA-PP和PSO-PP模型的评价结果在排序及评价结果上差异明显.表明智能算法极值寻优能力越强,其获得的适应度函数值、最佳投影方向越好,评价或计算精度越高.从图1及表6的评价结果来看,MSA、TLBO算法寻优精度优于DE、CA,远优于PSO算法.
4)从表6 MSA-PP模型对实例的评价结果来看,全省16个州市水资源脆弱性评价投影值处于1.078 2~2.996 5之间,即处于“重度脆弱/Ⅳ”~“轻度脆弱/Ⅱ”之间.其中,昆明、玉溪、曲靖、楚雄4州市水资源脆弱性评价为“轻度脆弱/Ⅱ”,对比原始数据来看,昆明、玉溪、曲靖、楚雄州4个州市经济社会相对发达,在用水效率(万元工业增加值用水量、万元农业增加值用水量、灌溉水利用系数等)、洪涝灾害(过闸流量大于5 m3/s水闸数量、地表水控制率、建成区绿化覆盖率、水土流失治理面积等)、旱灾(水库总库容占供水总量之比、供水量模数、节水灌溉率等)3个方面表现较优.由于怒江州、迪庆州经济社会发展相对落后,人口稀少,水源工程建设、水环境治理、洪旱灾害治理投入相对不足,致使在用水效率(万元工业增加值用水量、万元农业增加值用水量、灌溉水利用系数)、水质(城市污水处理率)、洪涝灾害(过闸流量大于5 m3/s水闸数量、地表水控制率、建成区绿化覆盖率、水土流失治理面积)、旱灾(水库总库容占供水总量之比、供水量模数、节水灌溉率等)4方面表现最差,其水资源脆弱性评价为“重度脆弱/Ⅳ”.其余评价为“中度脆弱/Ⅲ”的州市主要在水质、洪涝灾害、旱灾3方面表现相对较差.对于昆明、玉溪、曲靖、楚雄4州市,宜进一步加大水环境综合治理投入,削减污染物入河量,有效改善水体质量,其水资源脆弱性可进一步减弱.怒江州、迪庆州应在大力发展经济的同时,采取加大工业、农业节水改造力度,提高用水效率,争取一批水源工程项目开工建设,加大洪旱灾害治理投入等,可有效减弱水资源脆弱性风险.其他州市应依据表现较差的指标,有针对性地提出工程和非工程改进、治理措施,水资源脆弱性还有进一步减弱的空间.
5 结 论
1)介绍了一种新型群体智能优化算法——蛾群算法(MSA).通过8个典型测试函数对MSA进行仿真验证,并与TLBO、DE、CA和PSO算法的仿真验证结果进行对比.结果表明,MSA寻优精度优于DE等4种算法,具有较好的全局极值寻优能力和收敛稳定性能,在求解高维、复杂优化问题时具有更好的求解精度和全局极值寻优性能.
2)遵行科学性、可量化、可操作、指标可获取等原则,从水量、水质、洪涝灾害和旱灾4个方面遴选28个指标构建区域水资源脆弱性评价指标体系和分级标准.提出MSA与PP技术耦合的MSA-PP水资源脆弱性评价模型,以云南省16个州市水资源脆弱性评价为例进行实例研究,并构建TLBO-PP、DE-PP、CA-PP和PSO-PP评价模型作对比.提出的模型及验证方法具有通用性,可推广应用于其他领域,对水资源脆弱性评价研究具有参考意义.
3)在实例研究中,MSA优化目标函数所获得的平均值和标准差均优于TLBO、DE、CA和PSO算法,再次验证了MSA具有较高的求解精度和收敛稳定性能.利用MSA求解PP技术最佳投影方向,可获得更佳的适应度值和最佳投影方向,有效提高了PP技术的评价或计算精度.
4)MSA-PP模型对云南省16个州市水资源脆弱性评价结果与TLBO-PP模型相同,但在排序上存在差异;与DE-PP、CA-PP和PSO-PP模型的评价结果及排序上均存在差异.其中,与CA-PP和PSO-PP模型的评价结果在排序及评价结果上差异明显,表明智能算法的优化性能及求解精度决定了评价或计算精度的高低.
5)MSA-PP模型对昆明、玉溪、曲靖、楚雄4州市的水资源脆弱性评价为“轻度脆弱”,对怒江州、迪庆州评价为“重度脆弱”,其余州市评价为“中度脆弱”.各州市结合上述分析结论,通过采取有针对性地改进、治理措施,水资源脆弱性尚有进一步减弱的空间.
[1] 曹永强,高 璐,朱明明,等.水资源系统脆弱性的评价方法及其应用[J].人民黄河, 2016, 38(9): 46-49.
[2] 陈 岩.流域水资源脆弱性评价与适应性治理研究框架[J].人民长江, 2016, 47(17): 31-35.
[3] 刘倩倩,陈 岩.基于熵权法的流域水资源脆弱性评价——以淮河流域为例[J].长江科学院院报, 2016, 33(9): 10-17.
[4] 刘倩倩,陈 岩. 基于粗糙集和BP神经网络的流域水资源脆弱性预测研究——以淮河流域为例[J].长江流域资源与环境, 2016, 25(9) 1317-1327.
[5] 吕彩霞,仇亚琴,贾仰文,等.海河流域水资源脆弱性及其评价[J].南水北调与水利科技,2012,10(1):55-59.
[6] Sullivan C A.Quantifying Water Vulnerability :A Multi-dimensional Approach[J].Stochastic Environmental Research and Risk Assessment,2011,25(4):627-640.
[7] 潘争伟,金菊良,吴开亚,等.区域水环境系统脆弱性指标体系及综合决策模型研究[J].长江流域资源与环境,2014,23(4):518-525.
[8] 姚文锋,张思聪,唐莉华,等.海河流域平原区地下水脆弱性评价[J].水力发电学报,2009,28(1):113-118.
[9] 陈 曜,丁 晶,赵 永.基于投影寻踪原理的四川省洪灾评估[J].水利学报,2010,41(2):220-225.
[10] 陈广洲,汪家权,解华明.粒子群算法在投影寻踪模型优化求解中的应用[J].计算机仿真,2008,25(8):159-161,165.
[11] 崔东文,姜 敏.差分进化算法-投影寻踪模型在水质综合评价中的应用[J].人民珠江,2016,37(2):97-101.
[12] 刀海娅,孙 艳.萤火虫算法-投影寻踪模型在云南省洪灾评估中的应用[J].水利经济,2015,33(6):22-25.
[13] 崔东文,郭 荣.SSO-PP模型在水源地安全保障达标评价中的应用[J].水利经济,2015,33(5):8-13.
[14] 崔东文.鸡群优化算法投影寻踪洪旱灾害评估模型[J].水利水电科技进展,2016,36(2):16-23.
[15] Al-Attar Ali Mohamed,Yahia S. Mohamed,Ahmed A.M. El-Gaafary,Ashraf M. Hemeida. Optimal Power Flow Using Moth Swarm Algorithm[J]. Electric Power Systems Research,2017(1):190-206.
[16] 崔东文.飞蛾火焰优化算法在承压含水层参数反演中的应用[J].长江科学院院报, 2016, 33(7): 28-33.
[17] Mirjalili S. Moth-flame Optimization Algorithm: a Novel Nature-inspiredheuristic Paradigm, Knowledge Based Syst. 2015,89:228-249.
[18] 崔东文. 基于改进BP神经网络模型的云南文山州水资源脆弱性综合评价[J].长江科学院院报, 2013,30(3): 1-7.
[责任编辑 王康平]
Application of Moth Swarm Algorithm and Projection Pursuit Coupling Model to Regional Water Resources Vulnerability Assessment
Cui Dongwen
(Wenshan Water Bureau of Yunnan Province, Wenshan 663000,China)
A new group intelligence algorithm, water resources vulnerability evaluation model, which is based on the moth swarm algorithm (MSA) and the projection pursuit (PP) technique, is proposed to study the vulnerability of water resources in 16 cities of Yunnan province. The water qualitity, water quality, flood and drought were selected from 28 indicators to construct regional water resources vulnerability evaluation index system and grading standard. Eight typical test functions were used to simulate the MSA, and compared with DE algorithm, (CA), teaching optimization (TLBO) algorithm and particle swarm optimization (PSO) algorithm. The optimal PP direction was optimized by using MSA, DE, CA, TLBO and PSO algorithms. The water resources vulnerability of MSA-PP, DE-PP, CA-PP, TLBO-PP and PSO-PP model was evaluated. The results show that:The MSA has better global optimization and convergence stability than the other four algorithms, and has higher accuracy in solving high-dimensional and complex optimization problems. The vulnerability of water resources in Kunming, Yuxi, Qujing and Chuxiong was evaluated as “mildly fragile” by MSA-PP model; “severe fragile” for Nujiang and Diqing, and “moderate” by other counties fragile. The evaluation results of MSA-PP model are the same as those of TLBO-PP model, but they are different in order of ranking. There are differences between CA-PP, DE-PP and PSO-PP model. The level of the evaluation of the merits of the evaluation.③The model proposed in this paper and the verification method are universal and can be applied to other fields.
water resources vulnerability assessment; index system; grading standards; projection pursuit; moth swarm algorithm; simulation verification
2016-10-25
国家水体污染控制与治理科技重大专项(201307102-006-01);院士工作站建设专项(2015IC013)
崔东文(1978-),男,教授级高级工程师,主要从事水资源管理保护及智能算法在水文水资源系统中的应用研究等工作. E-mail:cdwgr@163.com
10.13393/j.cnki.issn.1672-948X.2017.04.003
TV213.4
A
1672-948X(2017)04-0010-09

