大跨度预应力混凝土连续箱梁桥横截面温度效应分析

邹鹤民

(中铁十六局集团第三工程有限公司,浙江 湖州 313000)

大跨度预应力混凝土连续箱梁桥横截面温度效应分析

邹鹤民

(中铁十六局集团第三工程有限公司,浙江 湖州 313000)

我国铁路规范中对于混凝土箱梁横截面温差分布已进行了规定,并给出了相应的温度应力计算公式,但公式中参数取值适用性和计算的温度应力是否准确还有待考证。今根据某座铁路预应力混凝土连续梁桥横截面现场长期温度实测数据,按照最小二乘法拟合得出该桥横截面竖向温差曲线表达式,并对实测温度工况应力状态进行了规范公式计算和有限元计算对比分析。结果表明,规范中给出的计算公式中参数取值与实测结果拟合的参数有一定的出入,按规范公式计算的温度应力与有限元计算的温度应力也有一定的差距。因此我国铁路规范中的混凝土箱梁横截面温差分布和计算公式有待进一步修正。

箱梁横截面；实测温度；温度梯度；温度应力

随着国家对铁路事业的更多投入以及技术的成熟,桥梁采用预应力混凝土连续箱梁桥形式也越来越多地得到普及[1-2]。连续梁桥的受力受很多因素影响,温度效应是其中不可忽视的一个因素。混凝土桥梁处于自然环境中,长期受到气温变化和太阳辐射等作用,又由于混凝土的热传导性能比较差,这样将导致混凝土箱梁桥表面温度升温明显,而箱梁内部温度依旧保持原来状态,于是混凝土箱梁结构在横截面上就产生了不均匀的温度场,进而产生了温度梯度[3-4]。而箱梁结构又是个超静定结构,能够阻碍由于温度梯度所导致的结构位移变化,于是就会在结构中出现附加应力,即为温度次应力。有时候温度次应力会很大,甚至超过荷载所产生的应力值[5],当结构所受拉应力值超过混凝土的抗拉强度时,结构表面出现裂缝,给桥梁造成一些危害。有资料表明,箱梁的顶板内侧经常出现纵向的裂缝,而腹板靠近顶板部位容易产生斜裂纹。箱梁受温度拉应力的部位与箱梁开裂的位置是基本吻合的[6]。因此,对预应力混凝土桥梁进行温度效应的研究是很重要的。文本就根据现场所测得的江山港特大桥横截面处的实际温度，对其温度效应进行对比分析。

1 中国铁路规范对温度效应的规定

1.1 规范对箱梁温差的定义

我国现行规范《铁路桥涵钢筋混凝土和预应力混凝土结构设计规范(TB 10002.3—2005)》[7]中对箱梁日照温差有如下的定义：有碴箱梁只考虑沿梁宽方向的温差荷载；无碴无枕箱梁应分别考虑沿梁高方向的温差荷载和两个方向的组合温差荷载。

箱梁温差分布图见图1,箱梁沿梁高、梁宽方向的温差曲线按下式计算

Ty=T01e-ay

(1)

Tx=T02e-ax

(2)

式(1～2)中:Tx、Ty为计算点y、x处的温差，℃；

T01、T02为箱梁梁高方向、梁宽方向温差(对于标准设计可按表1取值)，℃；

y、x为计算点至箱梁外表面的距离，m；

a为按表1取值，m-1。

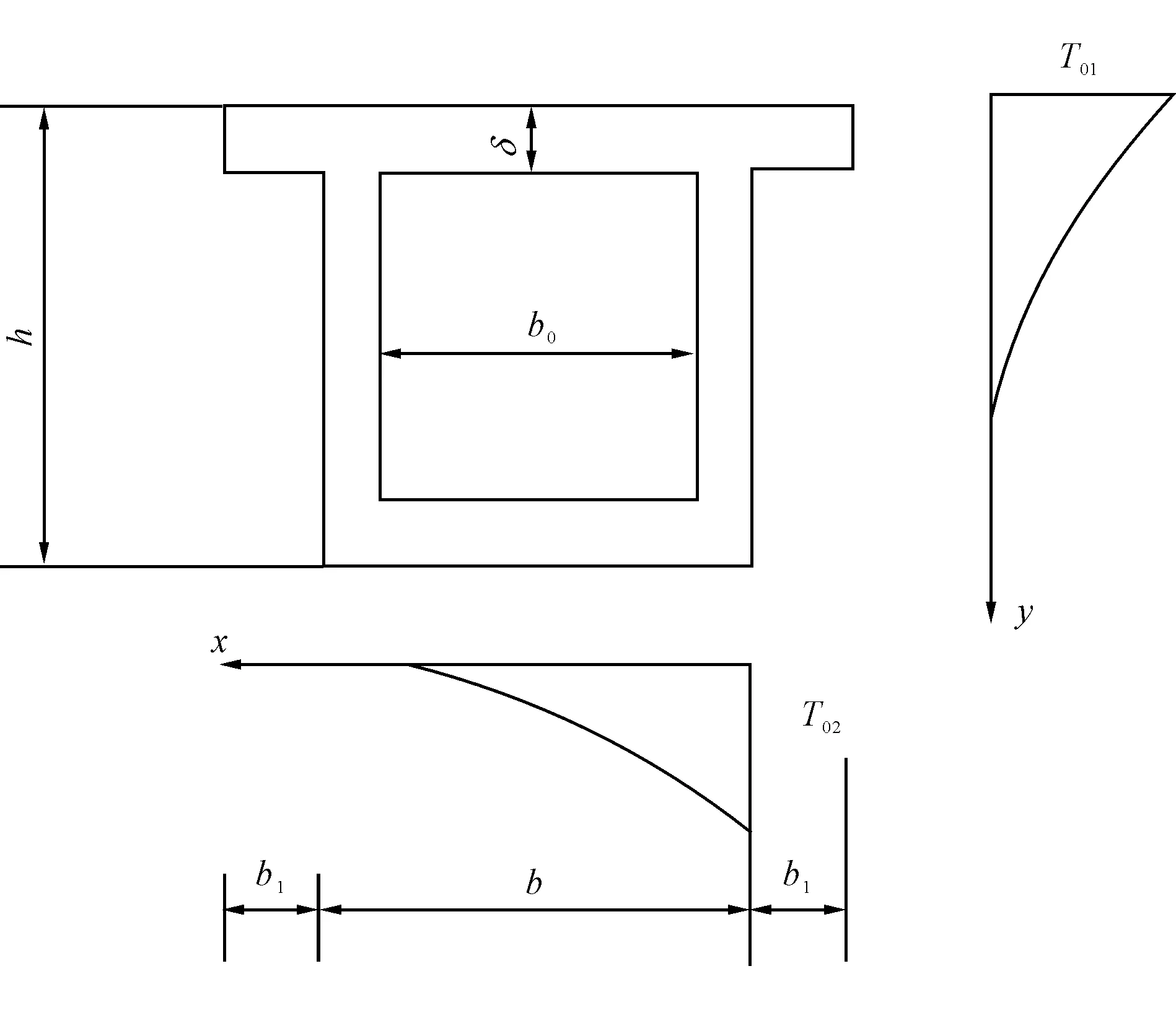
图1 箱梁温差分布图

表1 日照温差曲线的a与T0值

1.2 规范对温度应力的定义

预应力混凝土箱梁的温差应力计算,按照规范的计算方法,须分别计算自约束应力和外约束应力。自约束应力又可分为板的自约束应力和箱梁的自约束应力；外约束应力则包括横向框架约束应力和纵、横向支承约束应力。但是，如果仅考虑箱梁横向日照温差应力的话,那么其应力值由板的自约束应力和框架约束应力两部分组成[8]。

板的自约束应力按下式计算

(3)

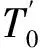
横向刚架约束应力按下式计算

(4)

式中：k为非线性修正系数,按规范中表B.0.3-1或表B.0.3-2采用；γ=b/h(b为梁底宽,h为梁高)；yi为板内计算点到外表面的距离,m。

2 工程概况与测试方法

2.1 桥梁概况

武冈城际铁路路口特大桥位于黄冈市黄州区路口镇,其中10～13号墩跨长河,河流与线路大里程夹角为52.737 4°,设计水位19.7 m,测时水位16 m,设计以(60+100+60) m连续梁跨越,设计行车速度为250 km/h,主墩承台结构10.5 m×14.3 m×4 m,边墩承台结构为7.8 m×11.1 m×2.5 m,墩柱结构形式为圆端型实体墩,梁体为单箱单室、变高度、变截面结构,箱梁顶宽12.2 m,箱梁底宽6.4 m,顶板厚度354～454 mm、454～554 mm,按折线变化,底板厚度400～1 200 mm,按直线线性变化,腹板厚度600～800 mm、800～1000 mm,按折线变化。全联在端支点、中跨中、及中支点处公设5个横隔板,横隔板设有孔洞,供检查人员通过。人行道栏杆内侧净宽12.1 m,梁全长为221.5 m,计算跨度为(60+100+60) m,中支点处梁高7.29 m,跨中10 m直线段及边跨15.75 m直线段截面中心线处梁高为4.69 m,梁底下缘按二次抛物线变化,边支座中心至梁端0.75 m。

2.2 试验方案

在主梁的根部截面以及四分之一跨截面处埋入若干温度传感器,分别于2012年10月2日、5日和13日在相同时间测试主梁各测点的温度。测试温度时,全天需测试4次,时间段分别为清晨8:00以前、上午11:00、下午15:00和傍晚18:00以后。将采集到的温度数据经过简单的整理分析,得出截面在不同时刻的温差分布情况,并依此按照规范规定的公式计算出温度应力值。

2.3 测点位置

测试截面为A-A和B-B两个截面,见图2。其中,A-A截面位于62#墩附近靠边跨侧主梁0#和1#块交界处；B-B截面位于主跨1/4跨9#和10#块交界处(靠近62#墩)。

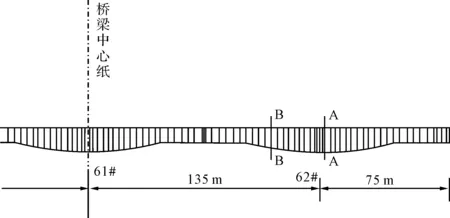
图2 温度测试截面布置图

A-A截面共埋设温度传感器42个,B-B截面共埋设温度传感器36个,测点编号见图3、图4。

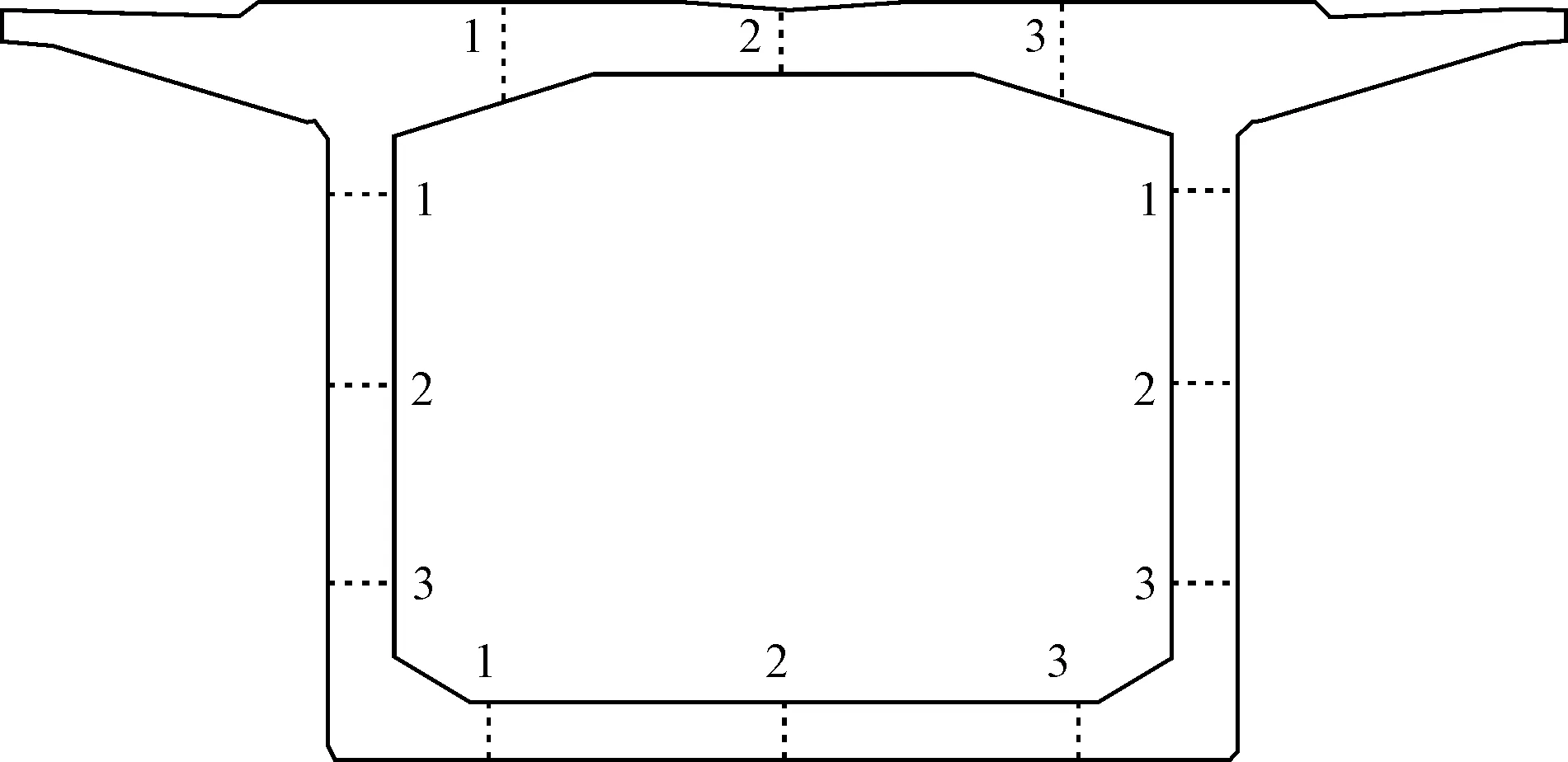
图3 A-A截面测点布置情况

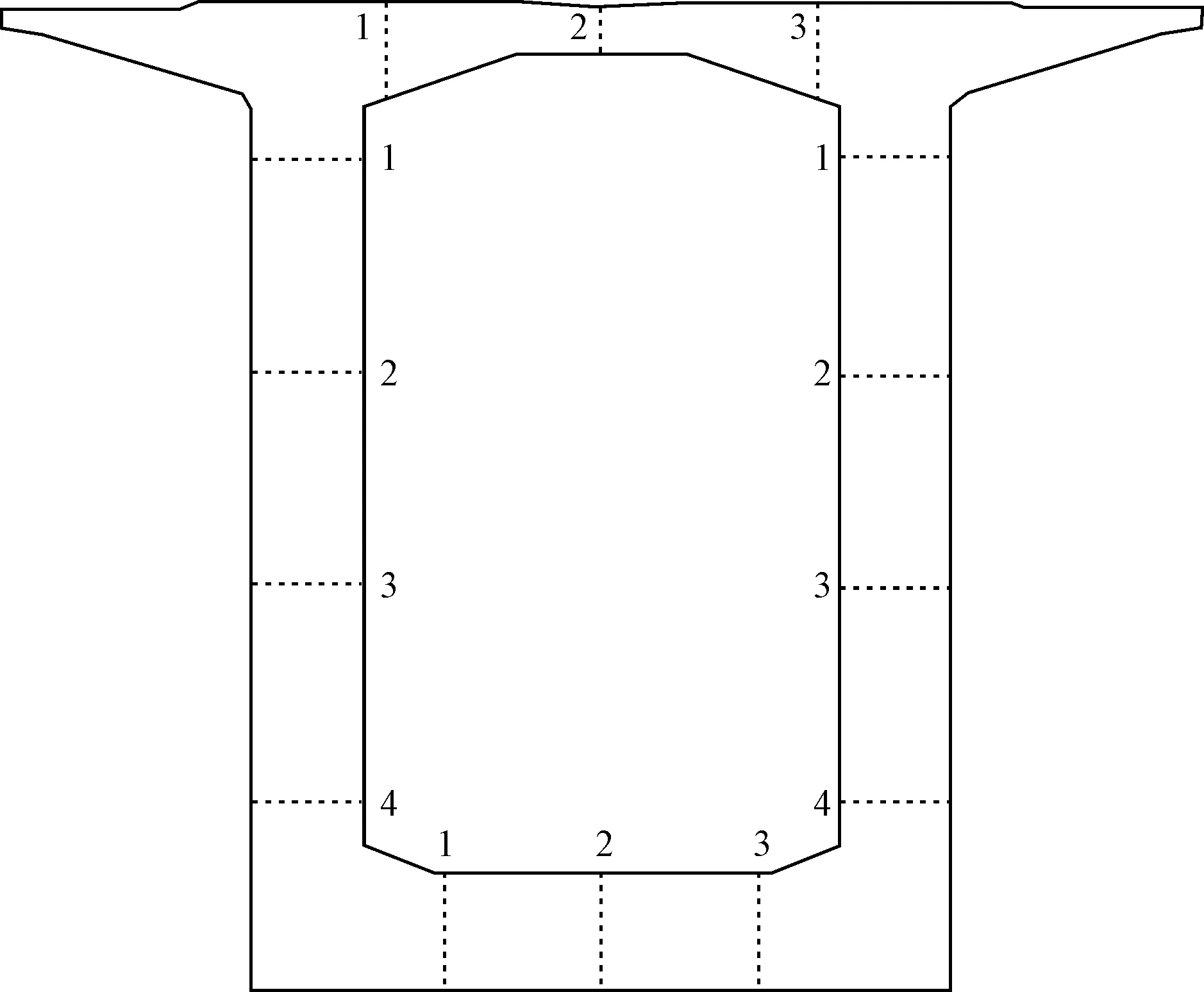
图4 B-B截面测点布置情况

3 试验结果分析

3.1 温度数据的处理

由于实际情况下测取了一天中4个时间段截面的温度值,而通常情况下截面横向温度应力最大值出现在温差最大时刻,所以有必要根据实测温度值推出最大温差发生的时间点并算出最大温差值,其中本节中顶板处与底板处的温差是根据顶板外侧温度值与内侧温度值之差所得。

根据实测温度值,腹板处温差最大值为2.6 ℃,差值不算很大,而且本文主要考虑横截面在竖向温差的影响下的受力性能,所以在此忽略对腹板温差的探讨,只对箱梁横截面顶板与底板处的温差作对比分析。根部截面和四分之一截面处顶板与底板处温差随不同时间点变化的规律见图5、图6。

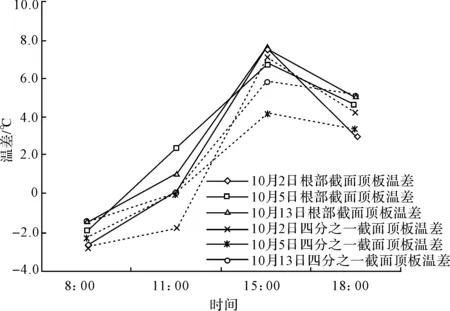
图5 顶板处温差变化规律图

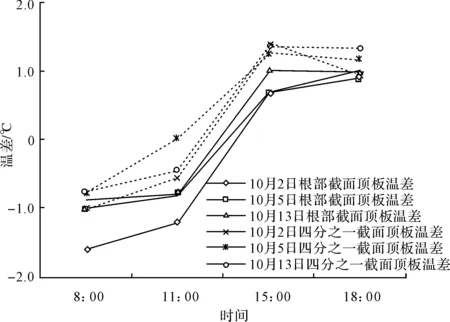
图6 底板处温差变化规律图

由图5、图6可知,根部截面和四分之一截面处顶板与底板处位置的温差变化规律基本相同。顶板处,由于太阳刚刚升起,温度还没有上升,早上8:00时的温差均为负温差,上午11:00时温差值在零附近,到了下午15:00时由于太阳长时间辐射的原因,温差变化明显,达到了一天中的最大值,下午18:00时,温度略有下降,故温差值略有下降,但依旧保持着正温差。底板处的温差主要是由太阳光照射到地面后反射到箱梁底部时所造成的,由于阳光强度没有直射的强度大,所以早上8:00与11:00时的温差均为负温差,当大气中气温逐渐上升时,底板处温差愈来愈大,在下午15:00左右达到最大,随着大气温度慢慢降低,底板处温差变化不是很明显,下午18:00时底板处温差基本与下午15:00时保持一致。

从图5和图6可以看出,根部截面顶板温差值要大于四分之一截面处顶板的温差值,而根部截面底板温差值却小于四分之一截面处底板的温差值,这说明截面的尺寸对顶板、底板温差分布规律具有一定的影响。由图5、6还可知,顶板处温差变化相对于底板处要明显,温差变化的幅度较大,温差最大值均发生在下午15:00左右,且顶板处最大温差为7.7 ℃,而底板处最大温差仅为1.4 ℃,相比起来,底板处的温差效应可以忽略不计。故本文以顶板处下午15:00时的温差值作为研究对象,来进一步模拟温度曲线的表达式,进而求得横截面横向应力值。

3.2 桥梁温度曲线的模拟

根据温度感应器所测得的各测点的温度值可以模拟箱梁桥横截面的温差分布曲线图。由于桥梁水平导热性不如竖向导热性好,而且纵向温度差异不大,故本文只考虑桥梁横截面的竖向温差。又因为本桥梁是无砟轨道,故根据规范可得横截面竖向温差曲线表达式为T=20e-5y。根据本试验所测得的数据,再根据最小二乘法原理,即可模拟出实测温度状况下横截面的竖向温差曲线。本文取梁体根部截面与四分之一跨截面处的实测温差曲线与规范规定的竖向温差曲线进行对比分析。

由于桥梁施工时间的影响,本文选取10月份所测得的3次温度测试值作为研究对象,对根部截面和四分之一跨截面进行对比分析。现将结果列于表2。

表2 温度测试值

由表2可知,在所测的日期中,桥梁根部截面和四分之一跨截面的竖向温差分布略有差别,但是总体来说具有一定的规律。

根据规范规定的温差曲线表达式可得T0代表的含义为温差的最大值,而a代表的含义就是温差减小的快慢程度。a值越小,就代表温差值在截面高度上减小得越慢；a值越大,就代表温差值在截面高度上减小得越快,而规范中规定的T0值为20 ℃,a值为5。

对于T0值,无论是根部截面还是四分之一跨截面,T0值均小于规范所规定的数值,即20 ℃,这可能是由于当时天气温度不是太高所导致的。但是根部截面的T0值均大于四分之一跨截面,这在一定程度上说明,桥梁横截面尺寸大小对其最大温差值具有一定的影响,并从表2中可初步推得根部截面的最大温差值稍大于四分之一跨截面的最大温差值。而这是规范中所未考虑的,说明规范对温差的定义还不够完善。

对于a值,根部截面的数值均大于规范所规定的数值,而四分之一跨截面的数值均略小于规范所规定的数值。这同时也说明桥梁截面的尺寸对温差在截面高度上减小的快慢具有一定程度的影响。并且,根部截面减小得要大些,四分之一跨截面减小得要小些。而这也是规范中所未考虑的,同样说明规范对温差的定义还不够完善。

3.3 利用铁路规范中的公式计算横向温度应力

根据规范所规定的温度应力计算公式和实测温度下的温差曲线分布,可以计算在实测情况下横截面的温度应力数值,并和规范下的温度应力数值进行比对分析。

将相关数据代入到公式中即可算出温度应力值,结果见表3表4,其中正值代表拉应力,负值代表压应力。

表3 根部截面处温度应力值 MPa

表4 四分之一跨处温度应力值 MPa

由表3、表4可知,横截面横向温度应力包含板的自约束应力和横向框架约束应力两部分,其中顶板顶层的温度应力表现为压应力,而顶板底层的温度应力表现为拉应力,这与结构力学中超静定结构受温度作用下拉应力总出现在温度较低侧的原理相符合[9]。且规范所定义温差作用下的温度应力均大于实测温差下的温度应力,这是规范定义的温差值相对实测温差数值要大些的缘故,温差越大,温度应力也就越大。而且顶板顶层的板的自约束应力要比横向框架约束应力数值大些,顶板底层的板的自约束应力却要比横向框架约束应力数值小些。同时,由表3、表4也可以看出板的自约束应力数值顶板顶层要大于顶板底层,横向框架约束应力数值顶板顶层与顶板底层相同,并且温差越大,温度应力数值也就越大。

根据表3、表4也可得出,规范定义的温差作用下,两个截面处温度总应力略有不同,其中四分之一跨截面的温度应力值稍大于根部截面的温度应力值。其中,两个截面处板的自约束应力数值完全相同,说明板的自约束应力与截面高度没有关系；而四分之一跨截面的横向框架约束应力值稍大于根部截面的相应值,这说明横向框架约束应力与截面的高度有关,且截面高度越大,横向框架约束应力值越小。然而，实测温差条件下根部截面和四分之一跨截面的温度应力值分布规律略有不同,主要是因为根部截面和四分之一跨截面的温差不完全相同所导致的,但是由于根部截面的实测温差大于四分之一跨截面的实测温差,故总体上根部截面的温度应力都大于四分之一跨截面的温度应力。

3.4 有限元软件计算截面横向温度应力

本节运用有限元软件MIDAS/CIVIL2010来计算横截面的横向温度应力,并与铁路规范下规定的横向温度应力值作对比分析。由于本节的目的是将软件计算结果与规范定义的公式计算结果作对比,故本节只考虑箱梁截面在规范所规定的标准温差曲线下的温度效应。

在MIDAS/CIVIL2010中选择梁单元对根部截面与四分之一跨截面进行建模,见图7、图8,然后对横截面顶板以及翼缘这些经常受日照温度作用的部位施加温度梯度荷载。由于软件中没有铁路规范中用指数函数来模拟温度分布的部分,故在此将指数形式的温度梯度沿着梁高方向转化成折线形的温度梯度,进而模拟指数形式的温度分布。

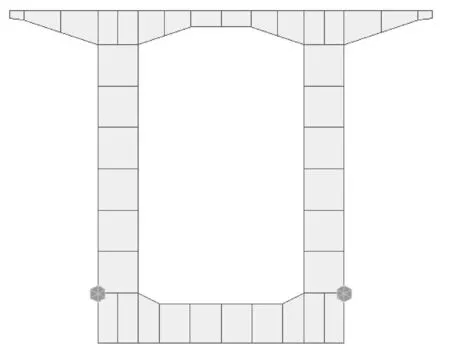
图7 根部截面有限元模型

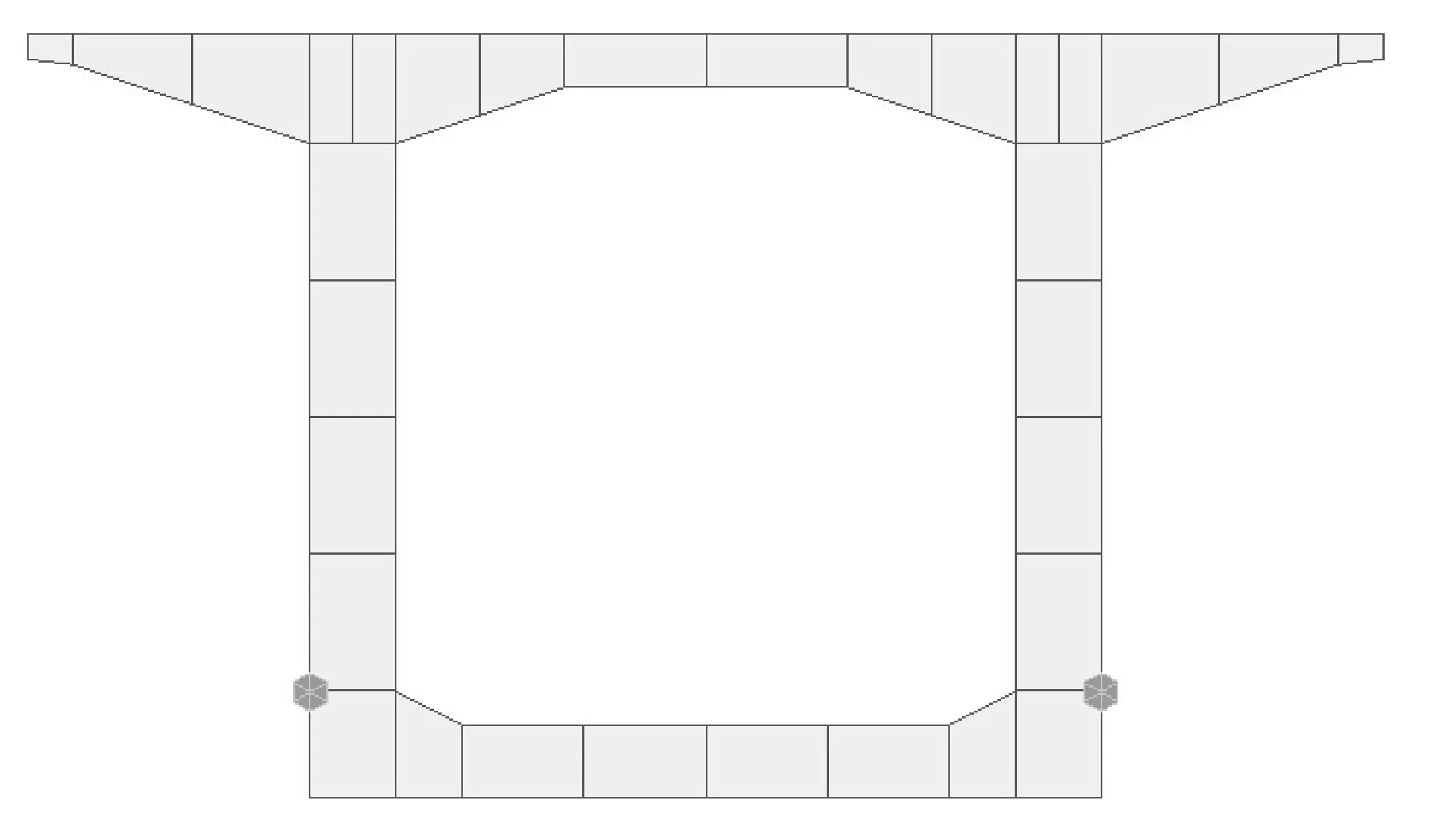
图8 四分之一跨截面有限元模型

经过有限元软件对横截面的分析,仅考虑竖向温度梯度的影响,不考虑底板处的温度梯度,腹板处以及底板处的横向温度应力值很小,在此就不列出来阐述分析。由于要和规范定义的公式所计算的温度应力值作比较,所以本节只提出顶板处的温度应力值来分析。根部截面顶板处与四分之一跨截面顶板处温度应力分布情况见图9、图10。

图9 根部截面顶板处应力分布图(单位:MPa)

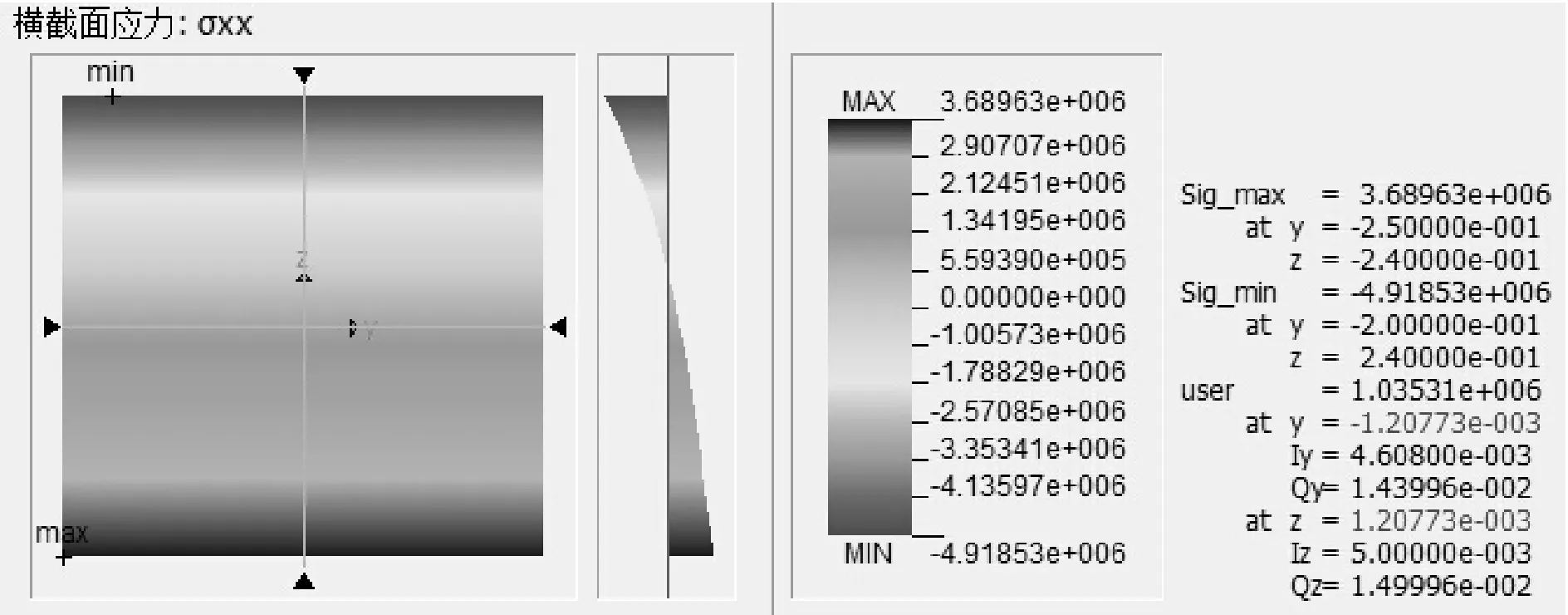
图10 四分之一跨截面顶板处应力分布图(单位:MPa)

由图9、图10可知,两个截面处顶板的横向温度应力分布规律几乎一样,在标准温度荷载作用下顶板顶层受压应力,顶板底层为拉应力。其中根部截面的顶板顶层边缘处压应力为5.66 MPa,顶板底层边缘处拉应力为4.44 MPa；四分之一跨截面的顶板顶层边缘处压应力为4.92 MPa,顶板底层边缘处拉应力为3.69 MPa。现将规范下计算的结果与有限元软件计算的结果列于表5、表6。

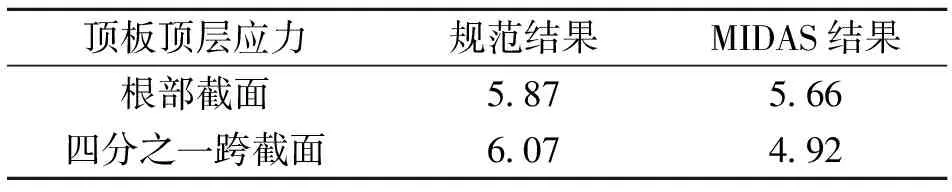
表5 顶板顶层横向温度应力值 MPa

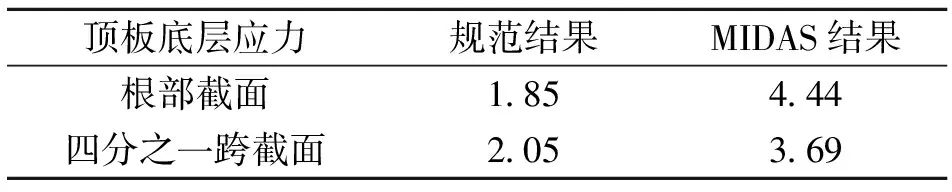
表6 顶板底层横向温度应力值 MPa

从表5、表6可以看出,规范中公式计算下的温度应力值与有限元软件计算出来的温度应力值差别很大,规范计算的结果是根部截面顶板处的应力值均小于四分之一跨相应处的应力值,而有限元软件算出来的结果却是根部截面顶板处的应力值均大于四分之一跨相应处的应力值,从中无法判断哪一种方法更加精确,故关于桥梁横截面的横向温度应力计算方法还有待于探索。

4 结 语

1)通过以上分析可知,温差最大的时候发生在下午15：00左右,且顶板处温差最大,腹板与底板处也有温差,腹板最大温差相对底板来说较大一些,而我国铁路规范中有规定箱梁截面的竖向温差与横向温差,但是忽略了底板处温差的效应,故我国铁路规范对于箱梁横截面温差分布的定义不完整,有待做进一步分析与完善。

2)通过对实测温度的分析,可以通过最小二乘法模拟出在实测情况下箱梁截面在竖向上的温差曲线函数表达式,通过对表达式的分析可知,根部截面与四分之一跨截面处温差曲线函数表达式不尽相同,根部截面得到的温差曲线表达式中系数均大于四分之一跨截面处得到的系数,这说明温差分布规律与截面形式有一定关系,而且截面越高,温差就越大,温差值在竖向减小得也越快。

3)通过计算可知,在温度荷载作用下,箱梁顶板的顶层受压应力作用,底层受拉应力作用,而且拉应力较大,如果温差很大,则温度荷载产生的拉应力将超过混凝土抗拉强度,导致箱梁出现纵向的裂缝,进而影响桥梁的耐久性。故需要在箱梁布置横向预应力筋,而且在顶板时要将钢束布置在顶板的底面,来承受温度荷载所产生的拉应力。而且根据十月份测量的3次温度值计算出来的温度应力值均小于规范规定下的温度工况计算出的温度应力值。

4)横向温度应力目前有两种计算方法,分别为通过规范公式的手算和通过有限元软件的计算,综合考虑,笔者认为规范下给出的计算公式较为简单,有些公式中列出的系数没有给出详细的说明,无法查到,而根据可以用到的公式算出来的应力值和有限元软件计算出来的结果也对不上,故规范中关于定义温度应力的公式需要进一步的研究。

[1] 范立础.桥梁工程[M].2版.北京：人民交通出版社,2012.

[2] 彭友松.混凝土桥梁结构日照温度效应理论及应用研究[D].成都：西南交通大学,2007.

[3] 叶见曙,贾琳,钱培舒.混凝土箱梁温度分布观测与研究[J].东南大学学报:自然科学报,2002(5):788- 793.

[4] 徐刚.箱梁温度场及其效应分析[D].上海:同济大学,2008.

[5] 高恩全,汤海良.大跨度连续梁桥温度应力计算分析[J].黑龙江交通科技,2007(12):88- 89.

[6] 龙佩恒.预应力混凝土箱梁桥开裂的数值分析方法[D].上海：同济大学,2005.

[7] 中铁工程设计咨询集团有限公司.TB 10002.3- 2005铁路桥涵钢筋混凝土和预应力混凝土结构设计规范[S].北京：中国铁道出版社，2005.

[8] 刘文法.预应力混凝土箱梁的温差荷载与应力检算[J].铁道标准设计，1986(6):1- 4.

[9] 龙驭球,包世华.结构力学[M].北京：高等教育出版社,1996.

Temperature Effect Analysis of Cross Section for the Prestressed Continuous Box Girder Bridge Concrete Bridge with Large Span

ZOUHemin

2017- 04- 06

邹鹤民(1983—),男，湖南涟源人，工程师，从事桥梁工程工作。

U442.5+3

A

1008- 3707(2017)04- 0048- 06