基于OPUS的空军航材随机备件决策模型研究

杨伟铁徐常凯张英峰

（空军勤务学院航材管理系徐州221000）

基于OPUS的空军航材随机备件决策模型研究

杨伟铁徐常凯张英峰

（空军勤务学院航材管理系徐州221000）

针对目前空军新机航材随机备件决策难的问题，对OPUS模型进行适应性改进，合理简化，优化算法，使其符合空军航材保障现状。并以某团实际航材随机备件方案为例，最后发现，无论在相同的飞机使用可用度或是相同费用的情况下，通过优化后模型得到的方案都明显的优于原始方案，验证了该模型的有效性。

随机备件；OPUS模型；使用可用度

Class NumberV267.31

1 引言

新机列装部队后通常有两年的工厂保障期，这个阶段内，航材的来源主要有两个部分：一是随飞机同步交付的随机备件（1∶1）。根据飞机数量按比例配置，用于飞机保证期内定期检修、维护保养，主要包括胶圈、胶垫、螺钉、螺帽、灯泡等价值较低的消耗性、易损性零备件和少量零组件，其费用计入飞机单价。二是军方集中筹措的初始备件。根据部队建制换装需要配置，用于飞机保证期内工厂服务组借用排故，主要包括故障率高、维修周期长的高价值可修性成品和轮胎、刹车片等日常消耗性航材备件，其采购费用不计入飞机成本，经费由保障部门在装备维修器材购置费中调剂解决。然而这样的备件保障方式却带来了许多问题。

1）作为随飞机配套赠送的随机备件，价值较低，而需要部队自己花钱购置的初始备件往往价格十分昂贵，不利于部队资金的流转。

2）工厂为了自身的利益，推荐的初始备件清单往往不够合理，如一些价格昂贵的备件推荐订购量较高，而一些常耗的价格偏低的备件推荐订购量却较少，一方面造成了大量资金的浪费，另一方面也不利于新机保障工作的开展。

3）工厂借用初始航材备件积极性不高。部队储备的初始航材备件通常为新品，工厂服务组从部队借用备件后，按照规定要归还同等级备件，但工厂服务组受经济成本制约通常无备件储备，无法做到“借新更新”，工厂服务组为减少自身保障成本，对初始备件借用积极性不高，进一步降低了初始备件利用率。

针对这些问题，按照军方主导、工厂主责的保障思想，改变传统初始备件由军方在飞机换装后向成品厂、辅机厂分散采购的航材筹措模式，实行大比例随机备件主机厂集中筹措负责制。飞机交付前，军方根据保障目标和经费指标，组织设计厂、所共同制定保证期内大比例备件清单，并安排经费，主机厂集中筹措，飞机交付时，航材备件与飞机同步交付。在这种模式下，随机备件包含以往的随机备件和初始备件两部分，因此，如何确定一个科学、合理的随机备件清单就显得尤为重要。

目前，航材随机备件的决策主要依据保障经验来决定器材的品种和数量，但由于对新机缺乏保障经验，同时新机本身的技术复杂、备件种类繁多和故障规律难以确定等，保障人员难以掌握有关备件的可靠性和保障性数据，因此造成了随机备件清单制定不科学、不合理的现象。针对这个问题，在对国内外现有相关模型深入研究的基础上，现以OPUS模型为基础，进行了适应性改进，并通过实际数据进行了验证。

2 国内外研究现状

2.1 国外研究现状

以美国为代表的西方发达国家很早就对航空备件决策优化模型开展了研究，有着比较丰富的经验，而且很多成果通过多次战争实践得到了验证和改良。应用较早的有经济订货（EOQ）模型［1］，主要用于消耗性备件的管理；此后还有基地存储模型（BSM）［1］、可修复器材管理多级模型（METRIC）［2］、飞机持续能力模型（ASM）［3］、以可用度为中心的库存模型（ACIM）［4］、航空部附件送修与分配动态管理模型（DRIVE）［3］等针对可修复备件管理提出的一系列模型。

几十年来，美国在备件优化决策模型领域方面的研究一直处于世界领先地位，其提出的模型具有极强的针对性和实用性，这些都为国内备件的相关研究提供了很好的借鉴价值。

2.2 国内研究现状

国内有关备件决策优化模型的相关研究大致可以分为两类，一类是直接采用国内外的模型和技术，如周伟等基于METRIC模型构建的两级供应关系的装备常用备件初始配置模型［5］；韩光林等基于OPUS建立的航空装备初始备件决策模型研究［6］。这些研究对METRIC及其衍生模型OPUS等如何在备件保障中进行实际应用，作了深入研究。另一类研究主要借助其他理论进行一些组配方法探讨。如周长玉、吴勇川等基于群智能算法对新机初始备件组配优化进行了研究［7］；王慧、宁彬根据不同种类备件寿命分布情况研究了军用飞机初始备件的配置方法［8］；倪现存、左洪福等利用价值工程分析法，研究了一种确定民机首批航材计划的方法［9］。

这些研究对初始备件决策优化模型进行了有益的探索，对航材随机备件决策优化有着一定的指导意义，但是这些研究的原理探讨较多，算法仍较为粗糙，实际运用的技术细节处理设计的较少，与空军随机备件保障的实际情况结合不够，模型需要的输入数据与实际保障数据存在较大差别，因此难以在航材随机备件保障领域中实际使用。

3 OPUS模型简介

OPUS数学模型是OPUS软件的后台数学模型，OPUS软件是瑞典SYSTECON公司开发的综合保障软件，适用于各类备件优化与费效分析。其核心思想是以费用为约束，以效能包括飞机使用可用度、不缺件概率等为目标，分析在一定费用下的最佳备件配置方案。该模型能够充分考虑多级备件保障组织间的关系，有着较强的实用性和灵活性，在许多国家的实际运用着也取得了不错的成效［10］。其决策原理见图1。

首先根据基层级LRU的需求量，结合备件的相关参数如修理层级、修复概率等，计算出基层级因修理LRU而产生的SRU需求量和因基层级LRU短缺而对基地级带来的LRU需求量。同样，基地级因修理LRU也会产生自身SRU的需求。然后从基地对SRU的需求着手，计算后方供应渠道补给的SRU数量，最后结合LRU后方送修与基层SRU补给延误的时间，计算基层LRU延误时间和期望短缺数，并由此计算出飞机的使用可用度。

4 模型的优化和改进

外军航材维修一般可以更换LRU和SRU，而我军主要更换LRU，因SRU延误而造成LRU短缺的情况几乎不存在，因此需要对图1中虚线框里的内容进行适应性改进。

4.1 基本假设

1）只考虑可修复件。因为不可修复件（消耗件）一般消耗量很大、价格却低廉，通常采取大批量订购原则，分析计算意义不大。由于随机备机主要用于飞机的前两年的工厂保障期内，时间较短，因此不考虑备件多次修理导致报废的情况，即认为可修复备件在工厂保障期内发生故障均可以修复。

2）备件寿命服从指数分布，备件需求服从泊松分布。一般来说，电子产品、复杂系统、经多次试验并进行定时维修的产品等其寿命服从指数分布。新机结构复杂、技术先进，其备件主要是电子产品和复杂系统，可以认为其备件寿命服从指数分布，而当备件寿命服从指数分布是，均可认为其需求服从泊松分布。

3）假定备件之间互不影响，相互独立。

4.2 备件需求量

各级备件保障部门的备件需求中，要消除SRU短缺造成的影响，也就是说因SRU延误而造成的LRU短缺均为0。本文根据现有的航材保障体制，分基层级、战区级和空军级三级分别进行计算。

基层级：基层j的备件年需求量为

式中，n为备件件数；t为备件平均修理周转期。

战区级：战区级z的备件年需求率，等于其所保障的所有基层单位发生对战区级z申请补给的备件需求之和。

式中，r0j为故障备件在基层级j修复的概率。同理，空军级备件的年需求率为

式中，r0z为故障备件在战区级z修复的概率。

4.3 备件期望短缺数

空军级的在修LRU件数的均值与方差分别为

式中，T0k为空军级维修站点对备件的平均维修时间。

令f0z为空军级向战区级z所补给的备件数量与占空军级备件需求量的比例。

战区级供应渠道平均数的均值和方差分别为

式中，t0z表示战区级站点z向空军级申请交付LRU的平均延误实践；T0z表示战区级站点z对备件的平均维修时间。

基层级备件供应渠道平均数的均值与方差的计算原理与战区级相类似，但需要明确地规定在整个保障体系中，每个战区级保障站点与各个基层级站点之间的组织关系，基层级LRU供应渠道平均数的均值与方差分别为

式中，f0j的含义以计算方法与战区级相类似，t0j为基层j向战区级z申请交付LRU的平均延误时间；T0j为基层级维修站点j对LRU的平均维修时间，j∈z表示战区级保障站点z所保障的所有基层级单位，根据保障站点之间的保障关系确定。

4.4 方案评估指标

目前，国内外通常用使用可用度来评价备件保障效能的高低，使用可用度是一项标征航空装备战备完好性的综合参数，是新机在航材保障系统下，处于正常工作时间的比例，但是飞机使用可用度的高低不仅和随机备件有关，而且会受到其他因素的影响，如航材的大修、定检等，因此，为了使评价结果更加准确、真实，还需要借助其他一些相关指标如不缺件概率等。

1）飞机使用可用度

假定组成飞机的备件都可用，则对于基层级j，飞机因缺某项备件而形成的使用可用度为

式中，s0j是基层级j的备件库存方案；Nj为该飞机在基层级j的总架数。

该飞机由N个备件组成，假定任何备件失效都会导致飞机出现故障不可用，因此，飞机使用可用度可以写为

2）不缺件概率

国内通常采用不缺件概率作为备件的评价指标，不缺件概率指备件i在库存为s时不发生备件短缺的概率，计算公式为

式中，s为库存数；p(k)表示发生k次需求的概率。在实际保障过程中，当某项备件的失效率［11］极低的时候，即使没有库存，也可能不会缺备件，而不缺件概率可以很好地评价这一情况。

4.5 模型算法

本文采用边际优化算法对备件方案进行决策，其核心思想是从最佳效费比的角度进行备件规划［12］。其中飞机使用可用度A0与系统的期望备件短缺数（EBO）有关，使飞机A0达到最大等效于EBO最小，其基本方法是：

所以随机备件方案优化问题可以归结为下面的整数规划问题：

其边际优化公式为

式中，δ表示期望备件短缺数的减少值和备件单价之比；EBO(s-1)表示现有数量为s-1个时的期望短缺数；EBO(s)表示备件现有数量为s个时的期望短缺数；C表示备件的单价。

5 实例分析

空军某团装备有20架歼-10型飞机，表1为其制定的随机备件目录（为了方便计算，随机选取了目录中的20项备件），假设备件保障单位各级之间申请交付的延误时间均为2天，备件的修理周期取该备件历次修理周期的平均值。通过边际优化算法，可以得到一系列保障方案，如图2所示。

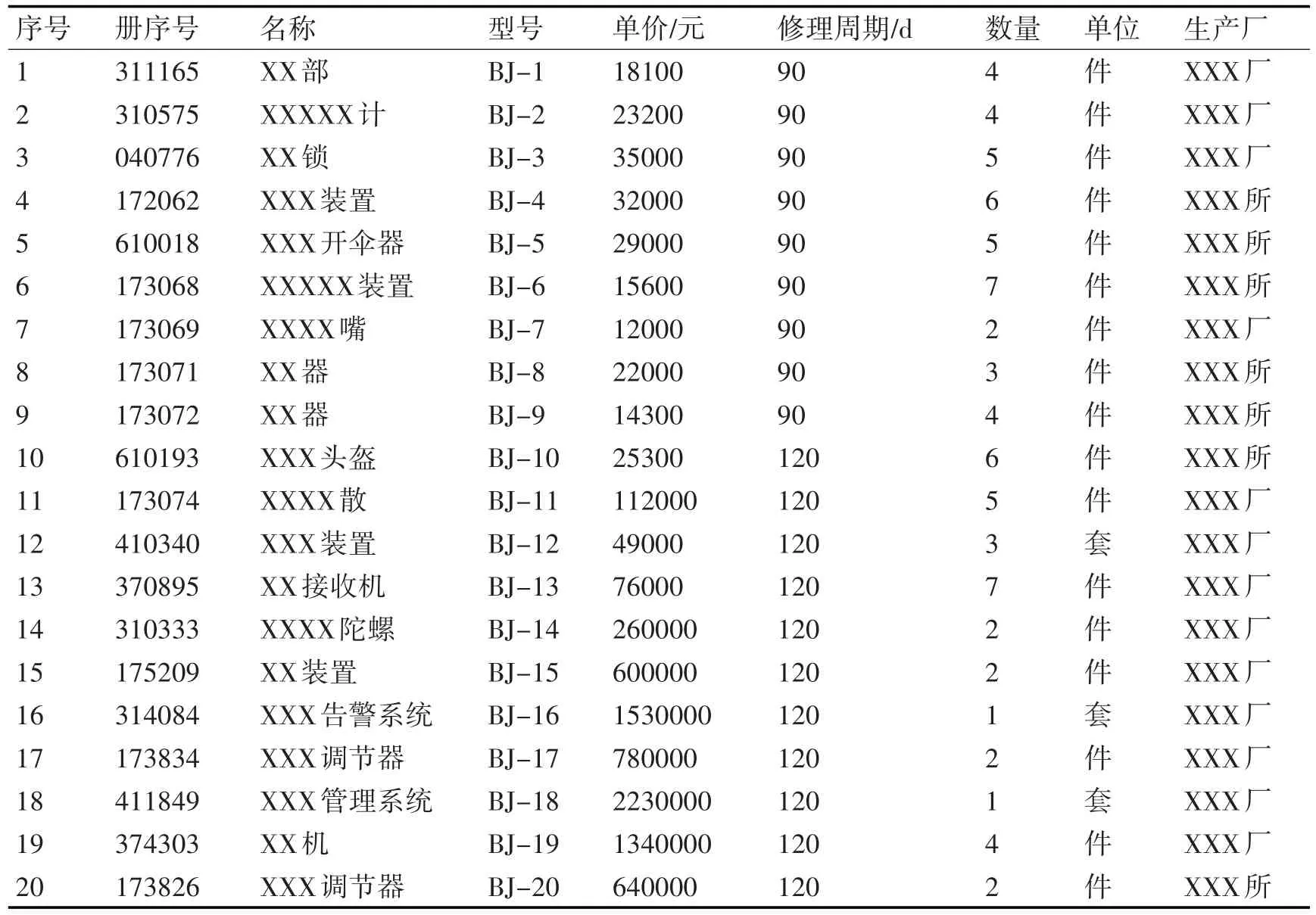
表1 随机备件目录

图1 中曲线上的任意一点，此点的横坐标代表这种方案下的总费用，纵坐标代表这种方案下装备能达到的最大使用可用度。把表1中原始随机清单目录里的相关数据输入OPUS软件，可以得到在原始方案下装备的使用可用度A=0.659，随机备件的费用L=16097200元。图1中还有两个特殊的点，一个是曲线上与原始备件方案具有相同费用的点，另一个是与原始备件方案具有相同飞机使用可用度的点。这两个点所代表的随机备件决策方案分别用Ⅰ和Ⅱ表示。

优化方案与原始方案的对比如下：

1）费用相同

原始方案：L=16097200，A=0.659；

优化方案：L=16097200，A=0.906；

飞机使用可用度提高约：0.247。

2）飞机使用可用度相同

原始方案：L=16097200，A=0.659；

优化方案：L=4970000，A=0.659；

费用节省约：11127200元。

方案Ⅰ的具体随机备件配置方案如表2所示。

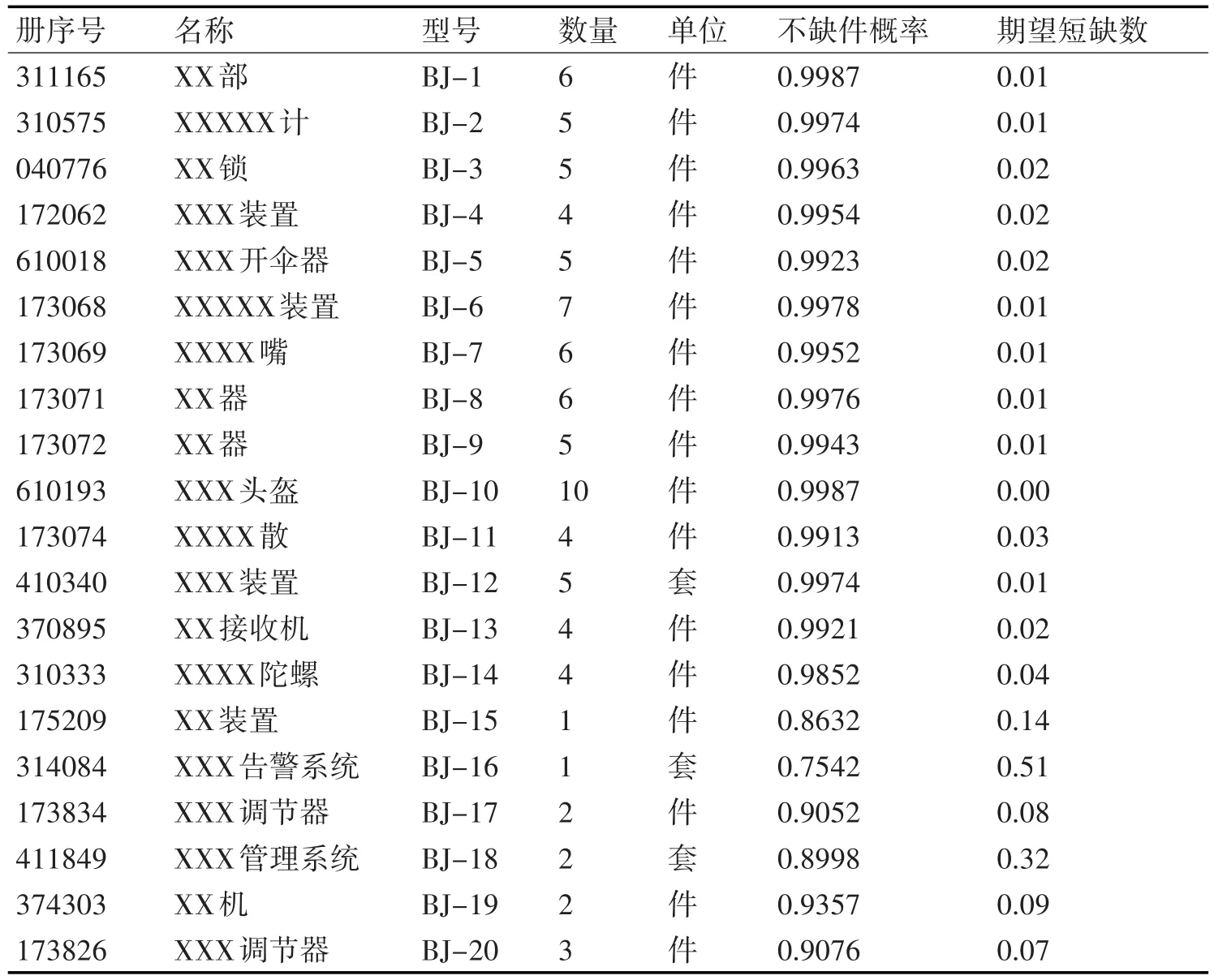
表2 方案Ⅰ随机备件配置清单

从表2可以看出，优化后的方案充分遵循了费效比最大原则，对于单价较低的备件如BJ-6，BJ-10等会尽量多储备；对于单价较高，故障率比较高的备件如BJ-11，BJ-14等按照优化原则适当储备；而对于单价较高，故障率较低的备件如BJ-15，BJ-19等则会尽量少的储备。另外，BJ-15，BJ-16由于购置数量很少，期望短缺数较高，是保障中需要重点关注的备件，在后期经费允许的条件下，可以适当增加订货量。方案Ⅱ分析与方案Ⅰ同理，这里不再具体说明。

6 结语

根据空军航材保障的实际情况对OPUS模型进行了适应性改进，对其内部算法进行了合理简化，使其更加符合空军航材随机备件保障的需要。通过实例可以发现，优化方案与原始方案相比，在相同的费用条件下飞机的使用可用度比原始方案高；而在相同的可用度条件下，费用又比原始方案低。当然，这只是一个理想化的结果，在实际保障过程中，还有许多未知的影响因素，期望本文的研究能够为新机随机备件的优化决策提供一定的参考。

［1］Hood W C，贺步杰，译.航材供运库存模型手册［M］.北京：国防工业出版社，2006.

［2］Sherbrooke C C.Multi echelon technique for recoverable item control［J］.Operations Research，1968；16：122-141.

［3］Sherbrooke C C.Var-METRIC：improved approximations for multi-indentured，multi-availability models［J］.Opera⁃tions Research，1986；34（2）：311-319.

［4］Hall F，Clark A.ACIM：availability centered inventory model［J］.Proceedings of the Annual Reliability and Main⁃tainability Symposium，1987：247-252.

［5］周伟，郭波，张涛.两级供应关系装备常用备件初始配置模型［J］.系统工程与电子技术，2011，33（1）：89-93.

［6］韩光林，阮元南，杨威.基于OPUS的航空装备初始备件决策模型研究［J］.科学技术与工程，2014，14（1）：114-117.

［7］周长玉，吴永川，张英锋.基于群智能算法的新机初始备件组配优化［J］.空军勤务学院学报，2012，23（6）：53-56.

［8］王慧，宁彬.军用飞机初始备件配置研究［J］.飞机设计，2012，32（5）：71-75.

［9］倪现存，左洪福，王华伟，许娟.价值工程在民机首批航材计划中的应用研究［J］.航空维修与工程，2007（6）：49-51.

［10］OPUS10 user's reference-system and logistics engineer⁃ing［M］.Sweden：Systecon AB，2002：25-30.

［11］GJB 451A-2005［S］.可靠性维修性保障性术语，2002.

［12］肖波平，康锐，王乃超.民机初始备件方案的优化［J］.北京航空航天大学学报，2010，9（36）：1059-1060.

Aviation Equipment Carried Spares Decision Model Based on OPUS

YANG WeitieXU ChangkaiZHANG Yingfeng
（Department of Air Material Management，Air Force Logistics College，Xuzhou221000）

At present，it is difficult for the air force to make a decision on carried spares.In order to solve this problem.An adaptability improvement is made on OPUS model—reasonable simplification and optimization algorithm to make it meet status quo of aviation equipment protection.By citing an actual carried spares scenario as an example，it is discovered that the optimized sce⁃nario is obviously superior to the original one whether the spares cost is invariable or operational availability is invariable，the model is verified as validity and rationality.

carried spares，OPUS model，operational availability

V267.31

10.3969/j.issn.1672-9730.2017.08.029

2017年2月10日，

2017年3月28日

杨伟铁，男，硕士研究生，研究方向：航材保障决策与信息化。徐常凯，男，博士，教授，研究方向：航材保障信息化与自动化技术、综合保障工程。张英锋，男，博士，副教授，研究方向：综合保障工程、航材保障信息化与自动化技术。