基于单二极管模型的光伏阵列建模与研究

魏 超，施火泉，许伟梁

（江南大学 物联网工程学院，江苏 无锡 214122）

基于单二极管模型的光伏阵列建模与研究

魏 超，施火泉，许伟梁

（江南大学 物联网工程学院，江苏 无锡 214122）

针对传统的光伏阵列模型精确性不高的问题进行分析，可知影响光伏阵列模型精确性的最重要因素就是光伏电池模型的选择。对常见光伏电池模型进行分析后以单二极管模型为基础进行光伏阵列建模。通过对模型求解策略和组件标准参数的处理来提高光伏电池模型的精确性。将采用不同求解策略和标准参数建立的光伏阵列模型在matlab中进行仿真，最后再将光伏阵列模型和带有MPPT控制算法的DC-DC变换器相连接。仿真结果表明采用解方程法并利用实际计算获得的标准参数建立的模型精确性更高，且所建立的模型能与带有mppt算法的仿真界面良好连接。

光伏阵列；单二极管模型；DC-DC变换器；MPPT

人们对于新能源领域的研究兴趣与日俱增，研究光伏发电的人员越来越多。光伏发电系统一般由光伏阵列和相应的电力电子变换装置组成。对于光伏系统研究者来说就需要有一个精确可靠的能和带有控制算法的电力电子仿真器件良好连接的光伏阵列模型。光伏电池是光伏阵列的最小组成单位[9]。要提高光伏阵列模型的精确性首先应该选择合适的光伏电池模型。光伏电池常见的3种模型分别为：基于单二极管的Rs模型[12]、Rs-Rp[10-11]模型和基于双二极管的D-diode[15]模型。除了选择合适的光伏电池模型外，模型的求解方法、在模型求解过程中对组件制造商提供的标准参数的处理也会影响模型的精确程度。对求解模型的各种方法进行分析后，选择了两种合适的模型求解方法。提出了一种通过实际测量和公式计算得到所使用组件实际标准参数的办法。最后将所建立的光伏阵列模型和一个带有MPPT算法的boost DC-DC变换器相连接进行仿真。

1 设计方案

1.1 光伏电池模型的选取

光伏电池Rs模型所需参数最少，但是在温度变化时模型的精确度比较低。D-diode模型精确度比较好但是需要计算7个参数，虽然可以通过简化减少参数的计算，但是简化也会对模型的精确度造成影响。所以本文在建模的方法上选择以单二极管为基础的Rs-Rp模型，其计算量合适精确度也较高[3，9]。等效电路图如图1所示，等效电路由电流源（Iph为光生电流）、反并联二极管（I0为流过反并联二极管的电流）、并联电阻Rp、串联电阻Rs组成。

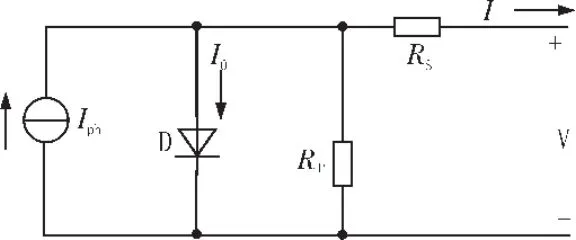
图1 Rs-Rp模型等效电路图

由基尔霍夫定律可得光伏电池输出电流特性方程[10-11]为：

其中q：电子电荷（q=1.6*1019C）；k:波耳兹曼常数（k=1.38*10-23J/K）；n二极管理想因子；Vt=nkT/q；T：光伏电池的温度。若干个光伏组件串并联组成光伏阵列，其输出电流特性方程如下：

Ns代表一个组件中串联的光伏电池数目。当若干个组件串联形成一个组件串时公式中的Ns表示为Ns=M*NC，其中M为一个组件串中串联的组件数，NC为单个组件中串联的光伏电池数目。NP为光伏阵列中并联的组件串数目。光伏组件制造商只提供给我们如下参数：开路电压Voc、短路电流Isc，最大功率点的电压和电流Vm、Im、短路电流点的温度系数a、开路电压点的温度系数β。所以我们需要用这些参数来求解方程。

1.2 光伏阵列模型输出电流特性方程的求解

我们可以通过解方程法或者工程简化法来求解光伏阵列模型的电流特性方程[3-6]。

1）解方程法

在开路电压点：I=0，V=Voc； 短路电流点：I=Isc，V=0；最大功率点：I=Im，V=Vm。将上述数据带入方程（2）中可得到3个求解方程。对于最后两个方程分别利用最大功率点处功率对电压的偏导数为0得：

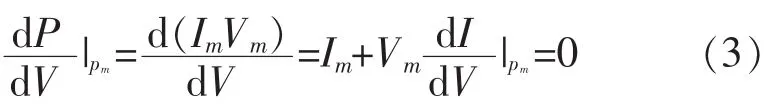
以及假定短路点的斜率近似为短路点与最大功率点的1/2得：

2）工程简化法[1，2]：

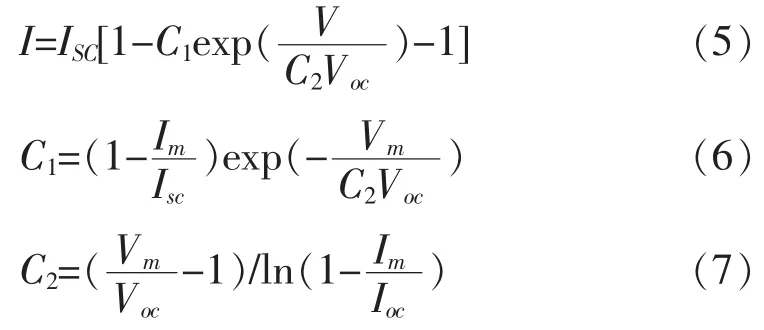
由（5）～（7）得到的为单个光伏组件的I-V特性，要得到N*M光伏阵列的I-V特性只需将电流乘以并联组件串数，电压乘以一个组件串中串联组件数即可。上述两种方法的公式中用到的组件参数（Isc、Im、Vm、Voc）都是实际工作条件下的参数，而组件制造商提供的参数 （Isc，ref、Im，ref、Vm，ref、Voc，ref） 都是标准情况（Tref=25°C，Gref=1kw/m2）下获得的，我们可以通过如下的转换公式[12，13]得到工作条件下的组件参数：

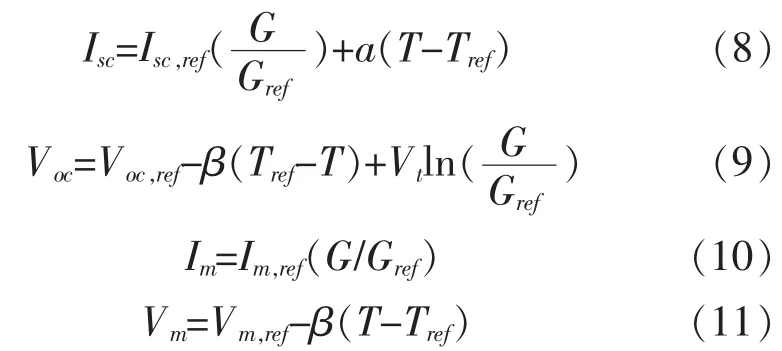
1.3 光伏电池模型的数据处理

在转化公式（8）～（11）中我们所使用的标准参数都是组件制造商提供给我们的，然而由于制作过程的误差以及随时间而产生的老化，每个组件的实际标准参数与制造商提供的不一定完全一致。为了消除这个误差，我们可以通过实际测量获得该组件的标准参数。所使用的公式[12，14]如下：

Gmea、Tmea为实际工作环境下的光照强度和温度，Isc，mea、Im，mea、Vm，mea、Voc，mea为在此条件下测得的组件参数。 利用（8）～（11）便可获得组件的实际标准参数（Isc，ref、Im，ref、Vm，ref、Voc，ref），此时再代入（12）～（15）中便可消除实际工作条件下组件的标准参数和制造商提供的标准参数不一致造成的误差。

2 仿真分析

光伏组件选用JAsolar生产的JAM6 60-250/SI。在标准测试条件下（T=25°C，G=1 kw/m2）光伏组件的参数如下：开路电压Voc=37.72V，短路电流Isc=8.76 A，最大功率点电压Vm=30.31V，最大功率点电流Im=8.2 A。 图 2（a）、（b）为在温度相同，光照不同情况下用解方程法和工程简化法建立的光伏阵列模型得到的I-V、P-V特性曲线和实验测试得到的曲线。从图中可知解方程法建立的光伏阵列模型更加精确。采用解方程法作为模型求解方法，在参数计算过程中分别采用制造商提供的标准参数和实际计算得到的标准参数，所建立的光伏阵列模型的I-V、P-V曲线和实验数据如图3（a）、（b）所示。从图中可知在参数计算中利用实际计算得到的标准参数所建立的光伏阵列模型更加精确。为了验证所建立的光伏阵列模型可以和光伏系统中其他仿真器件良好的连接，我们将其与一个含有MPPT控制器的DC-DC变换器连接[7，8]。 MPPT控制器采用传统的扰动观察法（P&O），DC-DC变换器采用boost结构。光伏阵列的结构为5*5。仿真过程如下：G=1 kw/m2时光伏阵列的最大输出功率6 270 W，在G=0.6 kw/m2时光伏阵列的最大输出功率为2 600 W。在t=0.5s的时候光伏阵列的光照强度由开始时刻由G=1 kw/m2变为G=0.6 kw/m2。从图4的boost DC-DC变换器输入功率的波形可以看出，在t=0～0.5s的时候输出功率经过短暂的上升过程后维持在6 270 W不变，当t=0.5s光照强度发生变化的时候，经过短暂的波动后输出功率维持为2 600 W。可见扰动观察法使得光伏阵列始终工作在最大功率点附近。

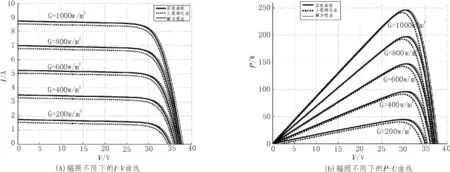
图2 温度相同，辐照不同下的I-V、P-U曲线

图3 不同的标准参数下I-V、P-V曲线

3 结论

分别用工程简化法和解方程法求解模型方程，建立了光伏阵列模型。通过仿真分析可知解方程法得到的光伏阵列模型精确度更高一些。

采用解方程法求解模型，在参数求解过程中分别采用制造商提供的标准参数和计算得到的标准参数，仿真结果表明参数计算过程中利用计算得到的标准参数所建立的模型更精确。

图4 boost变换器输入端电压、功率、电流

将所建立的光伏阵列模型和带有MPPT算法的DC-DC变换器仿真模型相连接，DC-DC变换器的输入功率在MPPT控制器的作用下始终跟踪光伏阵列的最大输出功率。验证了本文所提出的光伏阵列模型和相应电力电子仿真系统连接时具有良好的工作特性。

[1]杨金孝，朱琳.基于Matlab/Simulink光伏电池模型研究[J].现代电子技术，2011，34（24）：192-194.

[2]管笛，刘忠洋.一种新的太阳能电池阵列数学物理模型[J].科学技术与工程，2011，11（30）:7379-7381.

[3]候金明，许鹏.正常光照条件下全工况光伏阵列通用Matlab/Simulink仿真模型[J].太阳能，2013（11）:31-36.

[4]孔祥雨，徐永海，曾雅文，等.一种求解光伏电池5参数模型的方法 [J].电力系统保护与控制，2013，41（22）:46-50.

[5]马帅旗.太阳能光伏电池建模及V-I特性的研究[J].电源技术，2013，37（8）:1396-1398，1405.

[6]范发靖，袁晓玲.基于MATLAB的光伏电池建模方法的比较[J].电气自动化，2012，41（2）:157-159，163.

[7]李洁，刘蕴达.光伏电池和MPPT控制器的仿真模型[J].电源技术，2012，36（12）:1836-1839.

[8]郭海霞，石明磊，李娟.基于matlab光伏发电系统的MPPT控制和仿真[J].山西农业大学学报：自然科学版，2013，33（1）:76-81，92.

[9]贺素霞.基于matlab的太阳能电池数学模型及输出特性分析[J].电子设计工程，2015，23（3）:93-95，103.

[10]Hongmei Tian，Fernando Mancilla-David，Kevin Ellis，et al.A-cell-to-module-to-Array detalied model for photovoltaic panela [J].Solal Energy，2012，86（9）:2659-2706.

[11]Kun Ding，Jingwei Zhang，Xingao Bian，et al.A simplified model for photovoltaic modules based on improved translation equations[J].Solar Energy，2014，101（1）:40-52.

[12]Pon Vengatesh R，Edward Rajan S.Investigation of cloudless solar radiation with PV module employing Matlab-Simulink [J].SolarEnergy，2011，85（9）:1727-1734.

[13]Aissa Chouer，Santiago Silvestre ，Nawe Sadaoui，et al.Modeling and simulation of a grid connection PV system based on the evaluation of main PV module parameters[J].Simulation Modeling Practice and Theory，2012，20（1）:46-58.

[14]Krismadinata，Nasrudin Abd Rahim，Hew Wooi Ping，et al.Photovoltaic module modeling using simulink/matlab[J].Procedia Environmental Sciences，2013，17（1）:537-546.

[15]Kashif Ishaque，Zainal Salam，Hamed Taheri.Simple，fast and accurate two-diode model for photovoltaic modules[J].Solar Energy Materials&Solar Cell，2011，95（2）:586-594.

Modeling and research of photovoltaic array based on single diode model

WEI Chao，SHI Huo-quan，XU Wei-liang
（School of IOT Engineering，JiangNan University，Wuxi 214122，China）

The accuracy of traditional PV array model is not high，after a detailed analysis shows that the most important factor affecting the accuracy of the PV array model is the choice of the PV cell model.Through the analysis of the common model of photovoltaic cells，the single diode model as the basis for PV array modeling.Through solving strategy of the model and method for getting standard parameter to improve the accuracy of the photovoltaic cell model.A photovoltaic array model which is established by using different solution strategies and standard parameters is simulated in the matlab，and then the PV array model is connected with the DC-DC converter with MPPT control algorithm.The simulation results show that the proposed model is more accurate，and the model can be well connected with the simulation interface with the MPPT algorithm.

Photovoltaic array； single diode model； DC-DC converter； MPPT

TN601

：A

：1674－6236（2017）15-0141-04

2016-06-21稿件编号：201606150

魏 超（1992—），男，安徽合肥人，硕士研究生。研究方向：光伏系统并网发电。