卫星天文导航自主定轨精度及误差分析

季 玮，白 涛，武国强，林宝军

（1.中国科学院上海微系统与信息技术研究所 上海 200050；2.上海微小卫星工程中心 上海 201203；3.中国科学院光电研究院 北京 100094）

卫星天文导航自主定轨精度及误差分析

季 玮1，2，白 涛2，3，武国强2，3，林宝军2，3

（1.中国科学院上海微系统与信息技术研究所 上海 200050；2.上海微小卫星工程中心 上海 201203；3.中国科学院光电研究院 北京 100094）

通过星敏感器和红外地敏观测星光角距是目前实现卫星天文自主导航最为工程可行的方法，但由于星上敏感器在测量过程中不可避免的会引入外部环境测量误差，导致观测量星光角距存在偏差，最终会造成卫星定轨结果不精确。为解决这一问题，结合实验数据分析，最终确定了敏感器存在的系统误差是造成卫星天文导航定轨精度较低的最大误差源，并利用最小二乘方法对敏感器系统误差进行标定，将标定之后的观测量通过卡尔曼滤波算法进行噪声消除，使观测量更加准确。最后，利用星上实际下传数据对此方法进行验证，取得了良好的效果。

敏感器误差分析；静态地敏；天文导航；星光角距；星敏感器

天文导航是一种重要的卫星自主定轨方法[1-2]，它仅需利用卫星自带的姿态敏感部件星敏感器、红外地平仪等，且不需要与外界进行任何的信息交互，是一种完全意义上的自主定轨方法。对低轨卫星、中高轨卫星和深空探测器，天文导航自主定轨方法都备受青睐[3-5]。

文中天文导航所研究的对象为北斗中高轨卫星，其有如下两大特点：

1）卫星轨道高度较高。因为天文导航的定轨精度是同卫星轨道高度相关的，这就对敏感器的性能和数据观测以及处理提出更高要求。

2）北斗卫星所使用的红外地球敏感器为静态地敏，而不是传统的扫描式地敏，其体积更小且重量也更轻，更主要的是静态地敏无扫描机构，其测量精度更高。

在本文中，首先，通过对星敏感器和红外地敏建立定轨数学模型，可知模型中参杂的误差噪声主要包含随机误差和敏感器系统误差两大部分。经对误差数据分析后，确定系统误差为定轨主要误差源。而后，根据敏感器数学模型，提出采用最小二乘的方法来实现对系统误差的标定；将标定后的星敏、地敏数据采用卡尔曼滤波的方法进行噪声消除。最后，拿取星上下传数据对此方法进行验证，同地面定轨结果进行比较，最终定轨精度明显提高。

1 自主定轨原理

1.1 星敏、地敏定轨方法

在利用星敏感器和地敏进行卫星自主定轨时，观测资料[6-7]是地心方向ρ和卫星位置矢量之间的星光角距θ，其测量方程为：

式中：r为惯性坐标系下卫星的位置矢量，V为观测噪声误差。

在地心惯性坐标系中，选取卫星的位置r和速度v参数作为状态变量

记观测量Y=θ，则测量方程（4）可重写为：

对式（6）在参考状态量X*处做一阶泰勒级数展开，可以得到

式（7）可改写为

式中：y为观测残差，Δx为参考状态量的修正值，H矩阵为观测矩阵，其具体形式为：

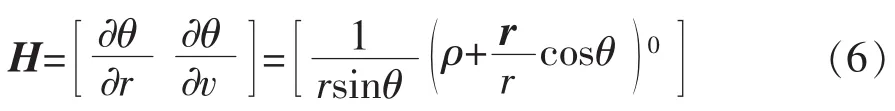
1.2 卫星轨道模型

导航卫星在轨道上运行所受的摄动力主要包括：地球质心引力F0、地球非球形引力FE、日月引力FN、太阳辐射压力FA、地球潮汐附加力FT、地球反照摄动力FAL等[8-9]等。

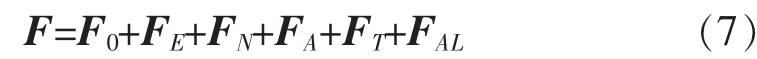
MEO导航卫星所受各种摄动力影响的最大误差如表1所示。从数据可以看出，轨道摄动影响最大的是非球形引力、日月引力、太阳光压，其他摄动影响较小，在计算中可以忽略。

表1 各种摄动力对MEO卫星的影响

1.3 Unscented卡尔曼滤波技术

由于自主定轨系统是非线性系统，而标准的卡尔曼滤波只能解决线性系统的估计问题，所以本文采用 Unscented卡尔曼滤波（UKF）算法[10-13]。

UT变换是UKF方法的核心和基础，考虑非线性变换y=f（x），则UT变换过程如下。

1）根据随机向量x的统计量x和方差Px，构造Sigma点集

其中κ是尺度参数，调整它可以提高精度。用这组采样点χi可以近似表示状态x的分布。

2）对所构造的点集{χi}进行f非线性变换，得到变换后的Sigma点集

变换后的Sigma点集{Yi}可近似地表示y=f（x）的分布。

3）对变换后的Sigma点集{Yi}进行加权处理，从而得到输出量y的均值和方差。

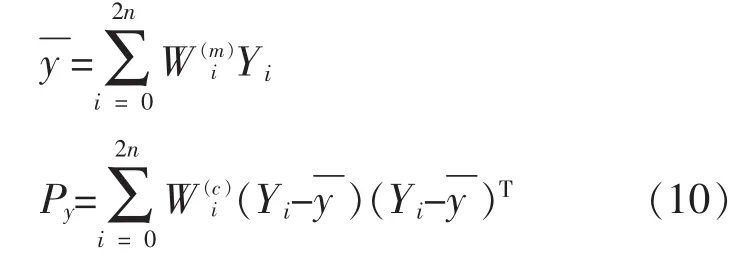
其中 κ=α2（n+λ）-n，1e-4≤α＜1，λ 通常设为 0，β为状态分布参数。

2 误差分析

星光角距是从卫星上观测到的导航恒星的矢量方向与地心矢量方向之间的夹角[14]，定轨误差影响因素将主要考虑以下误差对定轨精度的影响：

1）定轨初始轨道误差；

2）星敏误差：30角秒；

3）地敏常值误差 0.05°，随机误差 0.04°。

分别考虑初始轨道偏差、星敏误差和低敏误差进行分析，其结果如表2所示。

表2 各误差对定轨精度影响

由以上分析可以得出，星敏、地敏的随机误差对定轨产生的误差在1 000m之内，可以通过滤波减小此随机误差带来的影响，而地敏常值偏差对定轨产生的影响较大，在40 000m左右，且不可通过滤波消除，所以需要对地敏的常值偏差进行估计标定。已知星敏感器有公式[15]

其中，Rbs为星敏坐标系到卫星本体系转换矩阵，Rbi为惯性坐标系到卫星本体系转换矩阵，Rsi为惯性坐标系到星敏坐标系转换矩阵。因此有公式

式中，Sbserr为卫星本体系下星敏感器安装误差矩阵表示，Sbs为卫星本体系下星敏感器设定安装矩阵表示。

而地敏感器有公式

式中，Vboutput为卫星本体系下地心矢量表示，Ebserr为地敏感器卫星本体系下安装误差矩阵，Ebs为地敏感器卫星本体系下默认安装矩阵，Esoutput为地敏感器测得的地敏参考系下地心矢量，Eboutput为地敏感器基于设定安装矩阵得到的卫星本体系下地心矢量。

式中，Vioutput为惯性坐标系下地心矢量表示

综合公式（14）（15）（16）可得

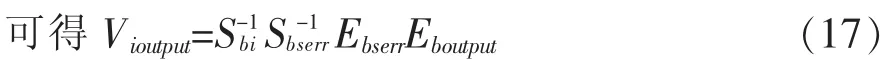
Vioutput可由轨道测量精轨求得，Sbi，Eboutput均可由星敏感器，地敏感器输出获得。因此，将误差矩阵S-1bserrEbserr看作一个整体，即可求得星敏感器，地敏感器整体安装偏差。

本文采用采集一段时间内地敏感器输出本体系地心矢量 Eboutput1，Eboutput2，Eboutput3…及该时段内星敏感器输出的惯性坐标系至本体坐标系下转换矩阵Sbi1，Sbi2，Sbi3…，与地面测得的卫星精确轨道位置向量Vioutput1，Vioutput2，Vioutput3…， 并利用最小二乘法对误差矩阵进行标定：

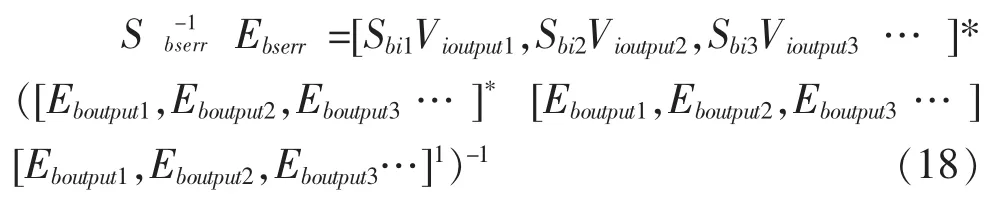
3 仿真分析

3.1 仿真设计

自主定轨仿真选取轨道根数为半长轴27 906km，偏心率1e-5，轨道倾角55°的中高轨卫星。用STK软件生成卫星精密轨道和星敏姿态四元数，分3种情况进行自主轨道确定仿真：不考虑地敏系统误差、考虑地敏系统误差但不估计、考虑地敏系统误差同时估计此系统误差。

3.2 仿真结果分析

3.2.1 忽略系统误差的自主轨道确定

首先只考虑观测数据的随机误差噪声，忽略地敏系统误差。定轨结果如图1所示，滤波稳定收敛后卫星惯性系三轴误差在1 000m以内，达到姿轨控定轨指标要求。

图1 星敏感器和红外地敏自主定轨误差（忽略红外地敏系统误差）

3.2.2 不估计系统误差的自主轨道确定

考虑红外地敏的系统误差，但不估计此系统误差。定轨结果如图2所示，红外地敏系统误差对定轨精度的影响十分显著，定轨收敛后位置均方差为34594m，考虑北斗中高轨卫星轨道高度一般为27 906km，由此可以计算出系统误差对定轨精度的影响为34 439m。

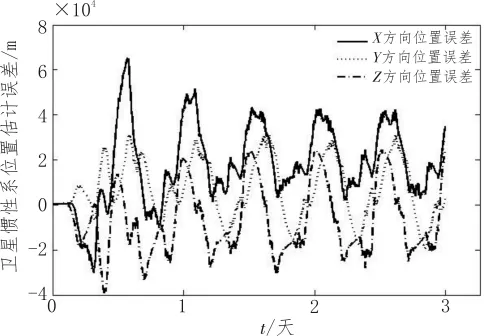
图2 星敏感器和红外地敏自主定轨误差（考虑红外地敏系统误差，但不估计）

3.2.3 估计系统误差的自主轨道确定

考虑红外地敏的系统误差，同时标定此系统误差。定轨结果如图3所示，滤波定轨稳定后，经数值计算其收敛后位置均方差为340m，达到姿轨控定轨精度要求。

图3 星敏感器和红外地敏自主定轨误差（考虑红外地敏系统误差，并估计标定）

4 在轨数据验证

由仿真结果可知，敏感器系统误差对定轨精度造成的影响不可忽视，对此系统误差进行标定后，可很大程度上提升卫星定轨精度，减小定轨误差。

选取3月1号星上下传的24小时延时遥测数据，根据对应时刻地面测定轨数值通过最小二乘计算出固定误差矩阵，分别对3月5日～7日和4月16日～18日星上数据进行验证，结果如下表3所示。

由上表星上数据定轨处理结果可以看出，如果对敏感器系统误差不予处理，仅通过滤波算法处理观测资料的随机噪声，最终收敛后的定轨精度在20km左右。通过1天的地面测定精轨数据，对系统误差进行标定后，定轨精度可提升至5km左右，定轨误差减小明显。

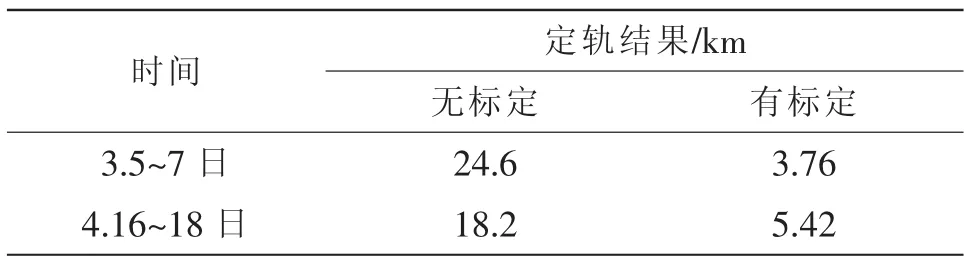
表3 星上数据定轨验证结果

5 结论

利用卫星自带的星敏感器和红外地敏实现卫星完全自主导航是当前工程上有效可行的方法。但观测资料存在的误差大大影响了天文导航定轨的精度，使得工程上无法有效应用。本文通过对敏感器观测资料可能存在的误差进行分析，论证了不同误差对定轨精度所造成的影响，得出以下几点结论：

1）敏感器系统误差为卫星天文自主导航定轨最主要的误差源，此误差不可通过滤波算法消除，若不能很好地处理则很难有效提升卫星定轨精度。而观测资料所携带的随机误差噪声可以通过滤波算法消除，对定轨影响在可控范围之内。

2）系统误差可通过地面短时间内的精确测定轨进行标定估计，对观测资料进行标定估计之后再通过滤波算法进行定轨，其定轨精度可提升75％，有效减小定轨误差。

此外，敏感器观测资料还可能存在同太阳位置或者敏感器温度相关的长、短周期误差，这可能是限制定轨精度进一步有效提升的原因。

[1]周建华，徐波.异构星座精密轨道确定与自主定轨的理论和方法[M].北京:科学出版社，2015.

[2]宁晓琳，房建成.航天器自主天文导航系统的可观测性及可观测度分析[J].北京航空航天大学学报，2005，31（6）:673-677.

[3]宁晓琳，王龙华.一种星光折射卫星自主导航系统方案设计[J].宇航学报，2012，33（11）:1601-1610.

[4]黄翔宇，荆武兴.基于“日—地—月”信息的卫星自主导航技术研究[J].哈尔滨工业大学学报，2002，34（5）:643-646.

[5]许承东，李怀建.GNSS数学仿真原理及系统实现[M].北京:中国宇航出版社，2014.

[6]马剑波，徐劲，曹志斌.一种利用星敏感器的卫星自主定轨方法[J].中国科学，2005，35（2）:213-224.

[7]尚琳，刘国华.利用分步Kalman滤波器的自主定轨信息融合算法[J].宇航学报，2013，34（3）:333-338.

[8]刘林，胡松杰，曹建峰.航天器定轨理论与应用[M].北京:电子工业出版社，2015.

[9]刘林，汤靖师.卫星轨道理论与应用[M].北京:电子工业出版社，2015.

[10]周海银，潘晓刚.卫星状态融合估计理论与方法[M].北京:科学出版社，2013.

[11]黄小平，王岩.卡尔曼滤波原理及应用[M].北京:电子工业出版社，2015.

[12]刘伟，杨博.利用UKF的航天器自主导航方法研究[J].航天控制，2005，23（3）:55-59.

[13]Dan Simon.最优状态估计——卡尔曼，H∞及非线性滤波[M].北京:国防工业出版社，2015.

[14]熊智，刘建业，郁丰，等.基于天文角度观测的机载惯性/天文组合滤波算法研究[J].宇航学报，2010，31（2）:397-402.

[15]章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社，1998.

The accuracy and error analysis of satellite autonomous celestial navigation orbit determination

JI Wei1，2，BAI Tao2，3，WU Guo-qiang2，3，LIN Bao-jun2，3
（1.Shanghai Institute of Micro-system and Information Technology， Chinese Academy of Science，Shanghai 200050，China；2.Shanghai Engineering Center for Micro-satellite， Shanghai 201203，China；3.Academy of Opto-Electronics， Chinese Academy of Science， Beijing 100094，China）

Using the star sensor and infrared earth sensor to observe starlight angular is the most project way to implement the satellite autonomous celestial navigation.But because of the external environment measurement error during the process of star sensor measurement.It will lead to the starlight angle has errors and finally cause the satellite orbit results inaccurately.To solve this problem，and combined with experimental data analysis，we ultimately determine the sensor system error is the main source of error which to cause the satellite autonomous celestial navigation orbit determination has the less accuracy.And using the least squares method to demarcate the sensor system error.To make more accurate observations， we use Kalman filter algorithm to eliminate noise of demarcate observations.Finally， using the actual satellite downlink data to validate this method and achieved good results.

sensor error analysis； static state earth sensor；celestial navigation； starlight angular；star sensor

TN98

：A

：1674－6236（2017）15-0090-04

2016-08-21稿件编号：201608153

国防专项（0301030104）

季 玮（1992—），男，江苏盐城人，硕士研究生。研究方向：航天器自主导航。