基于成本与时效的铁路空车调配优化模型研究

闫建文，魏玉光

(北京交通大学交通运输学院，北京 100044)

【交通运输】

基于成本与时效的铁路空车调配优化模型研究

闫建文，魏玉光

(北京交通大学交通运输学院，北京 100044)

针对既有的铁路空车调配问题研究缺乏可靠性，且模型多数使用货主满意度的情况，本文提出了一种考虑时效性的空车调配多目标优化方法。通过分析铁路空车调配过程，基于成本与时效性，定义了空车调配过程的可靠性，建立了运输企业成本最小和运输效益最大的多目标优化模型，并计算得到整个过程的可靠性值。最后，应用LINGO编程软件进行了实例计算，与既有研究方法比较的结果表明，该方法的实用性良好。

时效性；空车调配；可靠性；多目标优化；LINGO

我国幅员辽阔，货物运输形成由北向南、自西向东的基本格局。铁路运输承担了主要的大宗货物和其他物资的运送任务，由于路网中各节点装卸车数往往不相等，这就产生了空车调配问题。合理的空车调配，将对降低运输企业成本、提高货运服务质量和加快路网的车流周转等起到重要的作用。

近年来，铁路空车调配问题取得了一些研究成果。Milenkovic等[1]运用库存理论来研究空车调配问题，建立了基于订货成本、持有成本和缺货成本最小的优化模型，基于塞尔维亚铁路网络的实例分析计算，对模型的适用性进行了验证。Narisetty等[2-3]基于货主需求，综合考虑运输企业成本和货主满意度，构建了双目标最优模型，并通过实例分析进行了验证。国内学者中，程学庆等[4-6]研究了铁路空车调配的多目标优化问题，建立了运输企业收益、货主满意度和路径合理利用均最大的多目标优化模型，并给出了求解思路。俞亦舟[7]运用定性与定量结合的方法，研究了车站代用条件下的铁路空车调配问题。这些研究往往集中在以空车走行距离最小或空车走行费用最小的单目标优化方面，由此确定的空车调配方案主要是从铁路运输企业的角度出发来降低其运输成本，但是会引发其他一些问题，如降低货主的满意度，导致铁路货源损失从而造成运输损失；运输路径由于采取最短路径容易造成铁路运输网络运输能力的不均衡，而给运输调整带来难度等。同时在调配过程中，一些随机事件如恶劣天气和通过能力变化等可能会破坏铁路运输网络，这些不确定性因素使空车调配具有动态特征。

针对上述研究缺陷，本文考虑货主关心的时效性问题，运用可靠性分析建立了基于成本和时效性协调优化的模型，并计算了可靠性值。这种多目标模型综合考虑了企业和用户两方的利益，能够较全面地反映实际情况下的铁路空车调配过程。

1 铁路空车调配的一般数学表达

铁路在以运输生产为出发点时，其一般的数学模型描述可表达如下[8]：设在路网中的空车供应站点有m个，用Si表示，i∈[1，m]，对应的空车数为ai；空车需求站点有n个，用Dj表示，j∈[1，n]，对应的需求数为bj；从供应站Si至需求站Dj的距离为lij，现需确定一组车流xij，使得其在设置的约束条件下，走行路程(或运输企业成本)为最小。据此建立如下数学模型：

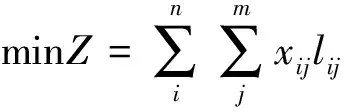
(1)

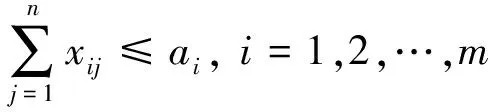
(2)

(3)

xij∈{0,2，…}，i=0,1,2，…，m，j=1,2，…，n，

(4)

其中，(1)式为目标函数，表示所求解的问题最优解，即使走行路程(或运输成本)最小；(2)式表示空车供应总数约束；(3)式表示空车需求总数约束；(4)式表示空车数应为整数。

上述约束条件的(2)、(3)式揭示了空车供应站与需求站的数量关系，两者相等时即为空车供需平衡问题；两者不相等则为供需不平衡问题。值得注意的是，上述模型理论上xij=0将是其最优解。然而在实际计算中，将不会出现这一情况。对于供需平衡问题，上述(2)、(3)式将变为等式，因而将不会出现xij=0的情况；对于供应大于需求的情况，(3)式将变为等式，求解时将不会出现xij=0，此时供应站将有空车剩余；对于供应小于需求的情况，(2)式将变为等式，因而也不会出现xij=0，此时需求未满足。对于产销不平衡问题，一般可以通过设置虚拟发站与到站，将其转化为平衡问题来解决。

2 基于成本与时效的铁路空车调配模型

上述模型是为了求解出最小的走行路程(或运输费用)，以便节约资金、降低成本。从根本上来讲，这是从铁路自身运营的角度来考虑空车调配问题，但未考虑到货主实际的运输需求。为了满足货主的需求，实际的铁路空车调配须在其运行计划中体现出来。既有的研究在处理这一问题时往往引入货主满意度的概念，建立相应的隶属函数，但在求解时却将其转化为费用问题，且参数的取值带有较大的主观性。本文从货主对时效性有一定要求的目标出发，考虑空车调配过程中存在的时效性问题，建立了一种新的空车调配模型。

2.1 问题描述

在路网中，有n个车站需要空车供应，有m个车站可供应其需要的空车，且已知货主期望的送达时间范围，基于此作出使运输企业成本最小且货主满意度最大的合理的空车调配方案。

2.2 模型假设

(1)不考虑技术站的作业时间；

(2)假定车流调整都是空车调整，不考虑以重代空以及车种代用因素。

2.3 模型构建

2.3.1 模型参数定义

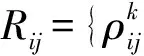
2.3.2 模型构建

从企业和用户的角度出发，分别建立了如下模型：

(1)铁路运输企业成本最小

考虑在进行调配时的铁路空车走行费用最低，建立空车供需调配模型如下：

(5)

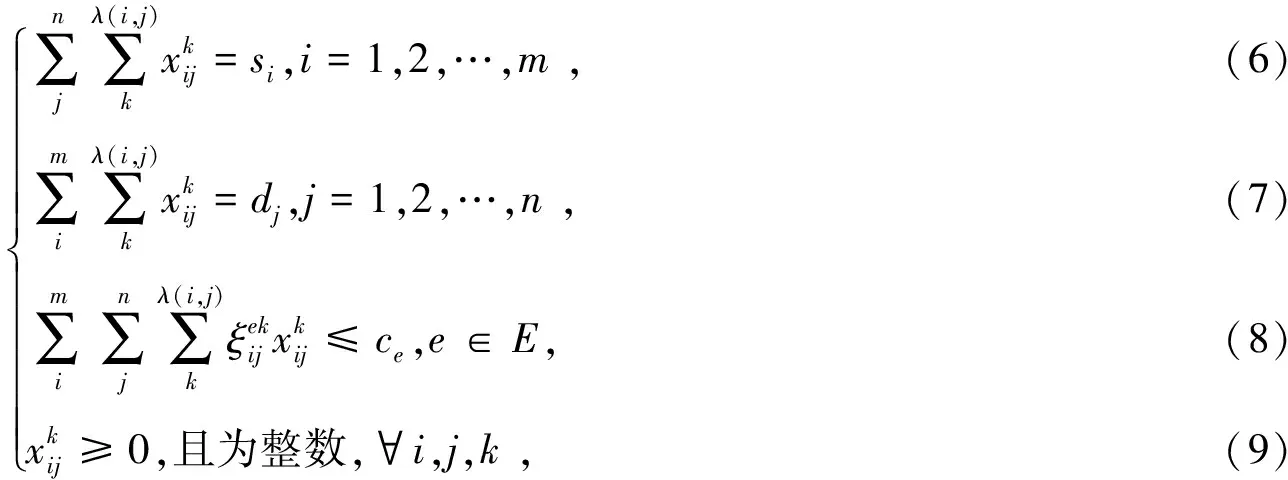
式(5)为目标函数，表示空车走行费用最低；式(6)表示i-j的空车数之和等于i站的总空车数；式(7)表示i站能够向j站供应的空车总数可满足j站的需求；式(8)表示对路段空车运输能力的限制；式(9)表示决策变量的取值约束。

(2)铁路空车调配的可靠性最高

实际中，货主往往关心空车能否在期望时间内到达。对于企业和货主来说，空车过早或过晚到达对二者均有不同程度的影响。在此不确定性情况下，考虑用可靠性[9]来度量货主的上述需求。铁路空车调配的可靠性可用在货主期望的时间要求内实际到达的空车数是否满足要求来度量，相应表示为各需求站在期望时间内空车的到达率均值来求解。

目标函数用效益最大化来表示：

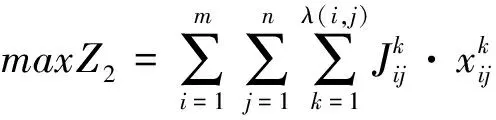
(10)

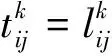
定义各站的到达时间可靠性为：

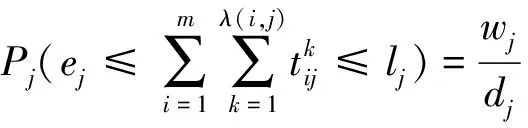
(14)

式(14)表示在货主期望的时间内，用空车需求站的实际空车到达数与其需求数量的比值表示整个过程中的空车到达可靠性。

整个铁路空车调配过程的可靠性值用各站所得可靠性均值来表示，计算公式如下：

(15)

3 模型求解

既有研究在处理上述问题时往往计算各分目标的最优解，然后采取加权和来处理，如典型的满意优化理论[10]，然而在实际工程优化问题中这种处理思路带有一定的脆弱性：

(1)各分目标单位不一致，难以作比较；

(2)加权处理时主观性成分突出；

(3)仅仅对各分目标的加权值求和以及通过决策变量来制约各目标，有时会出现相互矛盾的结果。

上述问题可看作满足约束条件下的多目标协调优化问题，核心在于解决目标冲突。为此本文考虑用多目标协调优化算法[11]来求解空车调配问题。

3.1 多目标协调优化原理

该方法对每个分目标做出一定的让步ε，然后找寻最小让步值ε0，以得到各分目标都可接受的折中解。

如果对∀x∈D，有

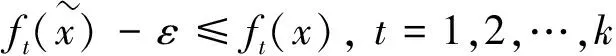
(16)

(17)

定义2 设x*为模型的一个优化后的可行解，ε0=min{ε|E(ε)}，即ε0是集合E(ε)中最小取值，如果x*是模型对应的ε0让步解，即

E(ε)={ε|ft(x*)-ε≤ft(x)，t=1,2，…，k} ,

(18)

则称x*是优化模型的折中解。

值得注意的是，一般情况下多目标优化问题的不同目标函数间往往具有不同的量纲，因此让步值ε表示不同函数间让步的相对值。满意解旨在通过搜寻最小的让步值来协调各目标值的冲突，达到优化目的。由于空车调配多目标优化问题可求得满意解，故将此求解问题等价转化成单目标规划问题。

3.2 求解步骤

对于有t=1,2,…，K个目标的铁路空车调配问题，先考虑各单目标的优化：

maxZt=minft(x)，t=1,2，…，k,

(19)

minZt=ε

(20)

求解上述模型，即得到空车调配多目标问题的最优解x*。

针对本文的铁路空车调配问题，两个目标函数成本最小和时效性最高具有不同的量纲，因此求解时ε表示二者间让步的相对值。

4 实例分析

设路网上有7个空车供需站点，其中供应站点3个，分别表示为S1、S2、S3；需求站点4个，分别表示为D1、D2、D3、D4。各车站的空车调整量及其运输距离和费用如表1所示，各供应站空车安排出发时间如表2所示，货主期望空车的到达时间如表3所示。

表1 各车站相应数据

注：需求站点数据表示距离(费用)，单位：公里(元)。

表2各供应站点空车的出发时间

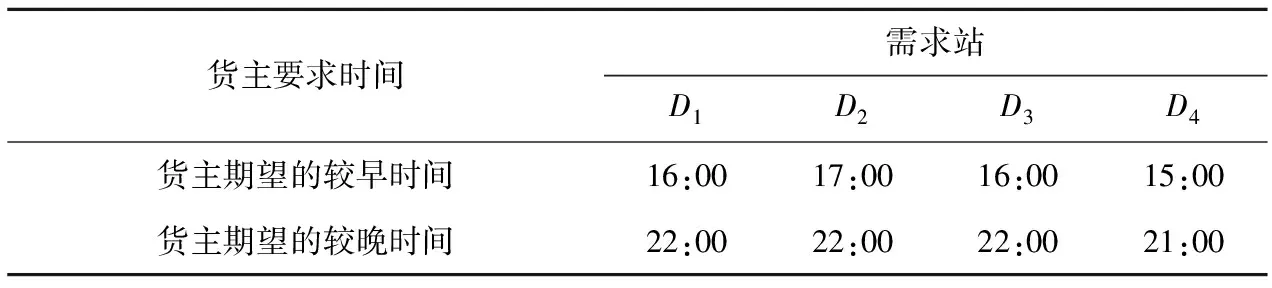
表3 货主时间要求

根据表1～3的数据，使用LINGO编程软件得到单目标的调配方案如表4～5所示。

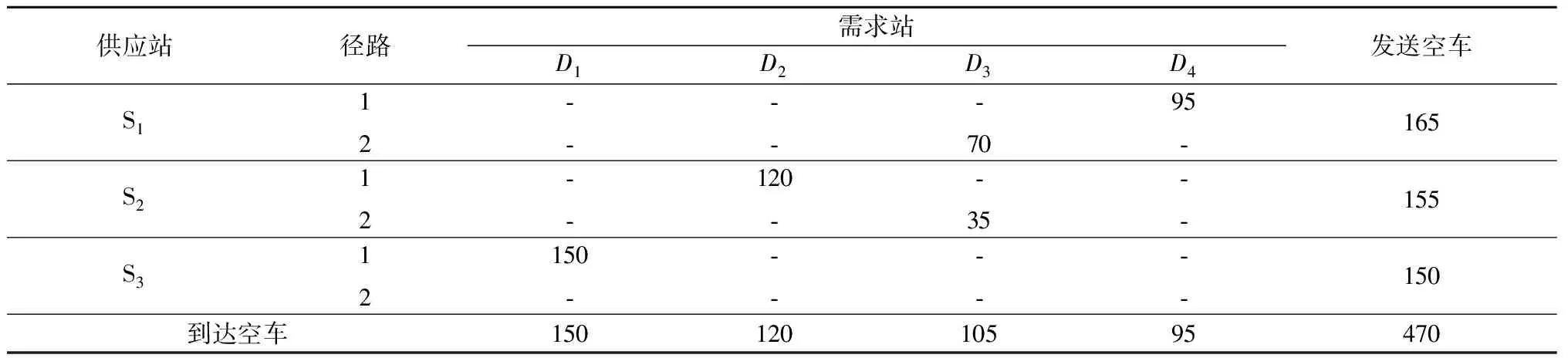
表4 运输企业成本最低的空车调配方案

表5 效益最高的空车调配方案

通过表5所示结果，计算各需求站的空车到达时间可靠性为：

计算整个调配过程的可靠性：

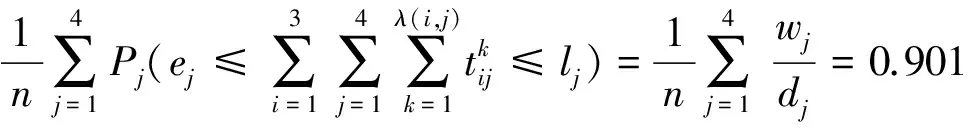
比较表4和表5的两单目标优化结果可知，运输企业成本最低的方案满足了实际的运输需求，而效益最高即时效性最优的方案满足了实际中货主关心的运输时效问题，但往往运输需求难以得到满足，此时的空车调配过程可靠性达到了90.1%，综合两方面要求得到相互协调的调配方案往往更有实际意义。

根据多目标协调原理构建新的空车调配LINGO模型，求解最优方案如表6所示。

表6 多目标协调的空车调配方案

通过表6所示结果计算各需求站空车到达时间可靠性为：

综上可知，在规定时间内空车调配过程的可靠性为：

表6所示结果考虑了企业和货主两方的要求，得到在实际调配过程中更有意义的运输方案。根据本文所论述的多目标协调优化原理，由于各分目标均存在让步值，因而对于可靠性而言，会有一定程度的下降。上述方案的调配过程可靠性达到了88.3%，较表5结果下降了1.8%，下降幅度在可接受范围内。

通过上述计算结果可知，与单目标的基于货主满意度的空车调配模型相比，多目标协调的空车调配可靠性有所下降，运输企业成本上升，体现了目标之间的协调性。在实际中，货主可与运输企业在签订合同时协商时间要求，所得的满意解及可靠性可作为运输企业和货主作出决策的依据。

5 结论

本文考虑时效性问题，将可靠性理论应用于求解具有动态性、模糊性的铁路空车调配的问题，构建了新的多目标空车调配模型，并计算出调配过程的到达时间可靠性，最后通过实例分析对模型的实用性进行了验证。本文的多目标模型对实际情况作了简化，未考虑调配时列车在技术站的作业过程，实例仅对一简化的路网进行了分析，在大规模路网下的模型适用性还有待验证。下一步的研究可考虑将车种代用、以重带空及技术站作业等因素加入模型，并通过实际的路网分析计算来说明模型的实用性，使模型更接近实际情况。

[1]MILENKOVIC M, BOJOVIC N. Fuzzy modeling approach to the rail freight car inventory problem[J]. Transportation Planning and Technology, 2014, 37(2): 119-137.

[2]NARISETTY A K, RICHARD J P P, RAMCHARAN D, et al. An optimization model for empty freight car assignment at Union Pacific Railroad[J]. Interfaces, 2008, 38(2): 89-102.

[3]JOBORN M. Empty freight car distribution at Swedish railways- Analysis and optimization modelling[D]. Sweden： Linköping University, 1995.

[4]程学庆.铁路空车调配综合优化模型及求解[J].中国铁道科学,2012,33(6):115-119.

[5]程学庆,陆一新,尹传忠,等.基于时间窗的铁路空车调配优化模型及求解[J].中国铁道科学,2007, 28(6):113-116.

[6]程学庆,蒲云.基于货主满意度的模糊空车调配模型的研究[J].铁道运输与经济,2007,29(11): 71-73.

[7]俞亦舟. 车种代用条件下铁路空车调配问题研究[D]. 兰州:兰州交通大学, 2013.

[8]熊红云,鲁五一，温红艳.铁路空车调配问题的遗传启发算法[J].中国铁道科学,2002,23(4):118-121.

[9]张戎,简文良,诸立超.铁路集装箱运输时间可靠性分析[J].铁道学报,2015, 37(11):10-15.

[10]方开莎.基于满意理论的铁路集装箱空箱调运优化方法[D]. 北京：北京交通大学,2010.

[11]熊国强,潘泉,张洪才.求解多目标运输问题的一种目标协调优化方法[J].系统管理学报,2007, 16(5):528-530.

Research on optimization model of railway empty wagon distribution based on cost and timeliness

YAN Jian-wen, WEI Yu-guang

(School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China)

∶Given that the existing study on railway empty car allocation lacks reliability and most models use owner satisfaction, a new multi-objective optimization model involved in timeliness was presented in this paper. By analyzing railway empty wagon and based on the cost and timeliness, the reliability of this process was defined, and a multi-objective optimization model with the least cost and the largest benef distribution it was established. Furthermore, the reliability value of the whole process was calculated. Finally, a numerical example was used to demonstrate the effectiveness of this method with LINGO software. Compared with the existing research methods, results show that the method proposed in this paper is practical.

∶timeliness；empty wagon distribution；reliability；multi-objective optimization；LINGO

10.3976/j.issn.1002-4026.2017.04.012

2016-11-24

中国铁路总公司科技研究计划(2015X004-B)

闫建文(1991—)，男，硕士研究生，研究方向为交通运输规划与管理。E-mail：15120907@bjtu.edu.cn

U292.45

A

1002-4026(2017)04-0073-07