例析线性规划中的交汇问题

陈国林 韩景岗

(1.赣南师范大学科技学院,江西 赣州 341000；2.山东省邹平县黄山中学，山东 滨州 256200)

例析线性规划中的交汇问题

陈国林1韩景岗2

(1.赣南师范大学科技学院,江西 赣州 341000；2.山东省邹平县黄山中学，山东 滨州 256200)

本文主要通过对近年的高考试题进行了分析，总结出了与线性规划交汇的九类问题，分别是简易逻辑用语、数列、解三角形、平面几何、函数、导数、复数、不等式以及向量等与线性规划结合.

线性规划;交汇;数学思想

线性规划及其思想有着很大的“包容”性，因此线性规划问题的题型新颖别致、多姿多彩，这已经成为了高考试题中的新亮点.下面以例题形式呈现其命题特点供读者参考.

一、线性规划与简易逻辑的交汇问题

A. 必要不充分条件 B. 充分不必要条件

C. 充要条件 D. 既不充分也不必要条件

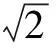
二、线性规划与数列的交汇问题

例2 (2010四川卷理)等差数列的前n项和为Sn，S4≥10，S5≤15，则a4的最大值是

三、线性规划与解三角形的交汇问题

四、线性规划与平面几何的交汇问题

五、线性规划与函数不等式的交汇问题

六、线性规划与导数的交汇问题

A．(1,3] B．(1,3) C．(3,+∞) D．[3,+∞)

七、线性规划与复数的交汇问题

八、线性规划与向量的交汇问题

[1]蓝云波，陈国林.解三角形问题还可以这样破解[J].数学通讯，2016(11).

[责任编辑：杨惠民]

2017-05-01

陈国林(1994.12-),男，安徽利辛人,从事数学教育研究.

G632

B

1008-0333(2017)19-0004-02

韩景岗(1977.01-)，男，山东邹平县人，一级教师，从事数学教育研究.