农业水资源多目标优化配置模型应用探讨
王玉伟,王光军,王玉立
(1.临清市水务局,山东临清 252600;2.临清市南水北调工程建设管理局,山东临清 252600)
农业水资源多目标优化配置模型应用探讨
王玉伟1,王光军2,王玉立1
(1.临清市水务局,山东临清 252600;2.临清市南水北调工程建设管理局,山东临清 252600)
结合临清市水资源开发利用现状,建立了典型区域水资源多目标优化配置模型,以合理配置典型区域水资源利用方案。
临清市;农业水资源;优化配置;模型求解
临清市农业水资源缺水量较大,为了满足当地农业生产需水要求,需要增加地下水开采,但是临清市已出现了大面积的地下水超采漏斗,应尽量减少地下水开采。为了确定临清市井渠灌溉模式,需要进行井渠灌溉优化分析,本文选择临清市内一个典型区进行井渠灌溉模式研究。
1 多目标优化配置模型
典型区内种植玉米和小麦,玉米和小麦在不同时期对水资源的需求量也不同,基于此选择采用非充分灌溉理论作为本次井渠灌溉水资源优化配置的理论基础。多目标优化配置主要使具有条件的区域通过井渠充分使用典型区域内可使用的水资源,保证典型区域在当前阶段内获得最大的经济效益,同时将典型区内的地下水位控制在合适变动范围内,不会导致典型区域局部出现土壤次生盐渍化和地下水超采漏斗等问题,而使典型区域生态环境和地下水系统得到保护,多目标优化配置模型构建如下:
1)阶段变量。主要种植农作物为M类,则假设该阶段变量为i=1,2,3,……,M。
2)状态变量。每一类农作物即各阶段内可利用水资源能够分配的总水量为Vi。
3)决策变量。在不同阶段,研究区域内各农作物可以分配得到的净灌溉水量即Qi。
4)目标函数。采用经济效益和地下水位相结合作为优化模型的目标函数。
首先以研究区域农业生产相对净效益最大为经济目标,即f1(0<f1<1),其计算公式如下:

式中Ak为第k种作物的种植面积,万hm2;YMk为第k种作物的丰产产量,kg/hm2;PRk为第k种作物的单价,元/kg;Bk(Qk)为由作物层返回的第K种作物在分配净灌溉水量Qk时的最大相对产量;E为各种作物净灌溉效益之和。
采用地下水水位埋深作为优化模型目标函数,即f2,f2值属于0~1,计算公式:


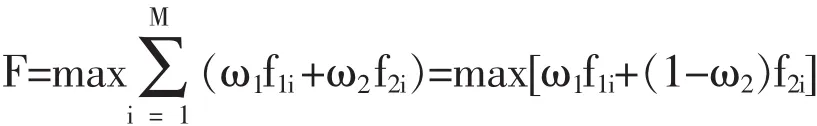
5)系统函数。指研究区域在各阶段各类农作物之间水量分配平衡方程如下所示:

式中:V为可用于分配的总水量,m3;Q为净灌溉水量,m3;η为灌溉水有效利用系数。
6)约束条件。根据构建的多目标优化模型和研究目的确定模型中各变量约束条件:0<Qi/η≤
其中:V0为研究区域总可供水量,m3,其余符号同前。
7)初始条件。依据研究区域提供的农业灌溉基础资料,确定优化模型的初始条件,主要是灌区可供水量,Vi=V0。
8)递推函数。模型求解利用逆序推理和顺序决策的计算方法,下面给出递推方程:

式中Ri(Vi,Qi)是状态为Vi时,决策为Qi时所得本阶段的效益;F*i+1(Vi+1)为剩余阶段的最大效益。
2 确定模型参数
2.1 可供水量
典型区域供水来源主要是地下水和引黄河水两部分。根据规划成果,分析计算得出临清市水资源总量和可利用量见表1。

表1 典型区水资源可利用量汇总表
2.2 降水量和需水量
由于在不同保证率条件下研究区域降水量是变化的。为分析典型区域农业灌溉年内分配情况需要了解研究区降水情况,同时需要预测不同频率的降水量以及年内分配,结果如表2所示。

表2 典型区域不同频率降水量预测结果mm
在不同保证率条件下研究区域的需水量也随之不同。依据典型区主要种植作物需水量分析,在保证率P=50%时,典型区农业灌溉需水量为240万m3;而在保证率P=75%时,典型区农业灌溉需水量为180万m3。
2.3 地下水位约束参数
依据典型区域地下水位观测资料和相关灌溉试验数据,采用数理统计和线性相关分析方法分析计算可知,典型区域在灌溉期间,地下水灌溉量和总灌溉量的比值与研究区域地下水位的关系:ΔHi=0.75-1.72Ti;在非灌溉时期,降水量与研究区域地下水位升降的关系:ΔHi=0.0137Pi-0.28。式中:ΔHi为灌溉后地下水位抬升和下降值,m;Ti为地下水灌溉量与灌溉总量的比值;P为阶段内降水量,mm。
2.4 其他参数
典型区主要种植作物为冬小麦和夏玉米,农作物复种指数为1.8。项目区内农业灌溉定额每亩为225 m3,灌溉水资源有效利用系数为0.45。
典型区域地下水埋深一般为3.4 m,为了防止典型区域出现土壤盐渍化,确定地下水埋深不易小于2 m;为了满足当地农业生产需水量则确定地下水水位埋深不宜超过4.6 m。依据典型区域相关资料和对相关参数的计算分析,可得到典型区内各类农作物相关数据。
3 模型求解
通过模型优化计算结果可知,当典型区为平水年时,优化模型的经济效益是5032.17万元;当典型区为枯水年时,模型优化结果是4332.61万元。由此可知:在平水年时,典型区域总灌溉水量为192.1万m3,与研究区域可供水量相比节约水资源27.9万m3;在枯水年时,典型区域总灌溉水量为198万m3,与典型区域在当前情况下可供水量相比节约2.4万m3。通过调整各阶段井渠灌溉水量使当地地下水位保持在适宜埋藏深度的附近,进而达到保护典型区域的生态环境和地下水环境,同时维持了灌区地下水开采和补给均衡。
(责任编辑 赵其芬)
TV213.4
B
1009-6159(2017)-08-0028-02
2017-01-02
王玉伟(1983—),男,工程师

