上软下硬地层地铁隧道与近接桥梁桩基的相互影响分区研究
仇文革, 雷 劲
(西南交通大学土木工程学院交通隧道工程教育部重点实验室, 四川 成都 610031)
上软下硬地层地铁隧道与近接桥梁桩基的相互影响分区研究
仇文革, 雷 劲*
(西南交通大学土木工程学院交通隧道工程教育部重点实验室, 四川 成都 610031)
依托青岛红岛—胶南城际轨道交通工程侧穿多座桥梁的工程实例,采用有限元强度折减法,对上软下硬地层桩基近接影响下的隧道安全系数变化规律进行研究。结果表明: 1)水平方向上,随水平净距增大,隧道安全系数增加,至1倍洞径后,安全系数趋于稳定; 2)竖直方向上,随埋深增加,隧道安全系数表现为先增大后减小; 3)桩基的存在将降低隧道安全系数,增加隧道达到最大安全系数所需的埋深。通过有无桩基对比,对不同相对位置关系下的地铁隧道近接桥梁施工影响程度进行判定: 1)总体上竖向的影响范围和影响程度均大于横向; 2)当隧道埋深位于桩底以上时,近接施工几乎只对隧道产生影响; 3)当隧道埋深位于桩底以下时,近接施工对于隧道和桥梁桩基均有不同程度的影响,当隧道位于桩底时达到最大。通过样条函数插值补全和多重二次曲面拟合的方法,给出影响系数通用分区图,并结合数值模拟下的桩基受力变形特征,得出影响系数0.8对应的等值线为强影响区与弱影响区的分界线,影响系数1的等值线为弱影响区与无影响区的分界线。通过影响分区结论与监测数据对比,验证了研究成果的实用性。
隧道近接桩基; 上软下硬地层; 强度折减法; 安全系数; 多重二次曲面拟合; 影响分区
0 引言
在我国现代化建设和经济发展中,交通建设一直扮演着相当重要的角色。在地理条件受到限制或需要更高精度运行条件时,通常采用桥梁跨江越海或隧道穿山越岭[1]。随着交通建设网的不断扩张,隧道与桥梁并行交叉的情况越来越多,其距离也越来越近。在隧道安全施工的同时保证既有桥梁基础的稳定,降低两者间的相互影响,将施工风险降到最低成为一个亟待解决的问题[2]。
目前对于隧道工程近接桥梁桩基的研究已经取得了一定的成果。郑熹光等[3]利用数值模拟研究了城市盾构隧道施工对邻近桥梁1桩、2桩、4桩基础的应力与位移的影响;杨超等[4]通过三维数值模拟发现隧道施工对临近桩基的影响不仅与隧道施工工况有关,而且也与桩基的位置、长度和数目紧密相关;王成等[5]通过有限元强度折减法计算了不同水平距离和桩基荷载下的隧道安全系数并对其分布变化规律进行了分析。
从现有的研究成果可以发现,以往的学者多以隧道或桥梁桩基中的某一个体作为研究对象,而并非将两者看成一个相互关联的体系来讨论; 且以往的研究对于两者间的影响程度及范围往往只给出了一个笼统的结论,缺乏系统定量的研究及对于两者空间位置关系对应的影响分区的深入讨论。
本文结合青岛地铁R3线出现的隧道近接既有桥梁桩基工程实例,采用数值模拟结合现场监测数据的方式,以基于强度折减法的安全系数为基础对工程影响区域进行划分,同时结合三维数值模拟隧道实际开挖过程中既有桥梁桩基的受力变形特征对影响分区进行优化,总结出上软下硬地层地铁隧道近接桥梁桩基的通用影响分区图。
1 近接影响分区标准和理论基础
1.1 基于强度折减法的影响系数
安全系数的定义有多种形式,但在隧道工程中,一般采用基于强度储备的安全系数[6]。由工程经验可知,静力条件下土体破坏大多表现为剪切破坏[7],在服从摩尔-库仑准则的前提下,对土体稳定性影响最大的强度参数是黏聚力c和内摩擦角φ[8]。将土体原始黏聚力c和内摩擦角的正切值tanφ同时除以一个系数ω,得到新的参数c′和tanφ′,再进行计算,直到土体到达极限平衡状态,此时这个系数ωcr就是强度折减的安全系数Fs[9-10]。其过程可以表示如下。

强度折减法在隧道领域中的适用性早已得到普遍认可,本文选用位移突变作为收敛判据[11-12]。有研究成果表明,隧道安全系数随着埋深的增加呈现出先增大后减小的总体趋势[13]。这表明隧道的破坏模式随着所处空间位置的改变也将随之产生变化,从理论上来讲,在开挖工法、地层条件等因素不变的情况下,隧道安全系数发生变化则必然受到周边建筑物及环境的影响[14-15]。
为了探究隧道近接桥梁桩基的影响规律并对其影响程度进行量化,本文通过有无桩基对比,将近接桥梁桩基的隧道安全系数记为Fsi,相同位置同等条件下无桥梁桩基的隧道安全系数记为Fsi0,两者安全系数之比Ki=Fsi/Fsi0称为影响系数。通过影响系数Ki对影响程度进行分区:Ki值越大,说明2种工况下隧道安全系数变化越小,桥梁桩基与隧道相互影响也越小;反之,Ki值越小,说明2种工况下隧道安全系数变化越大,桥梁桩基与隧道相互影响也越大。当Ki减小到某一数值后,认为桥梁桩基与隧道间的相互影响已相当严重,可将其临界值作为强影响区和弱影响区的分界值,本文先不妨假设为0.75。当Ki达到最大值1时,认为两者互不影响,该情况下可视为2个独立的建筑工程,故将1作为弱影响区和无影响区的分界值。
同时影响程度是相对的,相互影响却是绝对的,对于桥梁桩基而言,受隧道近接施工影响,其桩顶沉降、桩体受力等也将发生改变,故通过桥梁桩基的受力变形特征对基于隧道影响系数的影响分区进行优化和调整,可得到更具有普遍性的通用影响分区。
1.2 多重二次曲面拟合
多重二次曲面拟合是利用多个二次曲面根据一定的权重比例组合在一起,对已知数据点进行拟合逼近的一种方法[16]。基本二次曲面的种类较多,通常情况下可选用圆锥曲面作为基本单元,其曲面方程式为

(1)
式中k为圆锥曲面的斜率。
若已知n个数据点zi(i=1,2,…,n),分别对应于(xi,yi)。分别以这n个已知点为顶点,可得到多重二次曲面函数基本方程组
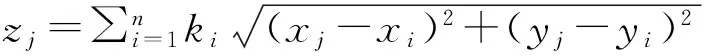
(2)
式中:i=1,2,…,n;j=1,2,…,n。
令


可将式(2)写成矩阵形式
Z=AK。
(3)
将已知数据点代入式(2)或式(3),求解系数矩阵K,则可得到多重二次曲面拟合方程式。
2 基于影响系数的影响区划分
2.1 计算工况设置
基于平面应变准则,采用FLAC3D建立计算模型,模型两侧及底部边界均大于5倍洞径,土体采用摩尔-库仑屈服准则,桥梁桩基采用弹性本构模型,桩基和土体间建立接触单元。结合青岛地层“上软下硬”的典型特征,模型从地表向下土体依次为素填土、强风化花岗岩、中风化花岗岩以及微风化花岗岩。为探究一般规律,本文将地铁隧道近接桥梁桩基工程抽象为如图1所示的基本模型。桩顶荷载根据相关规范结合实际工程估算荷载集度p为2 MPa。在计算过程中,隧道毛洞采用全断面开挖一次成型,不考虑初期支护、辅助工法等的影响。

(a) 整体模型轮廓(单位: m)

L为桩基长度;B为隧道跨度;D为隧道与桩基最外侧间的水平净距;H为隧道埋深;p为荷载集度。
(b) 模型细部
图1 基本模型
Fig. 1 Basic models
材料物理力学参数参照相关地勘报告和规范进行取值,如表1所示。

表1 物理力学参数
注: 桩基与土体的接触面参数中法向、切向刚度均为对应土体体积模量和剪切模量之和的10倍,黏聚力、内摩擦角均为对应土体的0.8倍。
将决定隧道与桥梁桩基空间位置关系的水平净距D和埋深H分别以隧道跨度B和桩长L之比进行替换,进行量纲一化,设置的42组工况如表2所示。
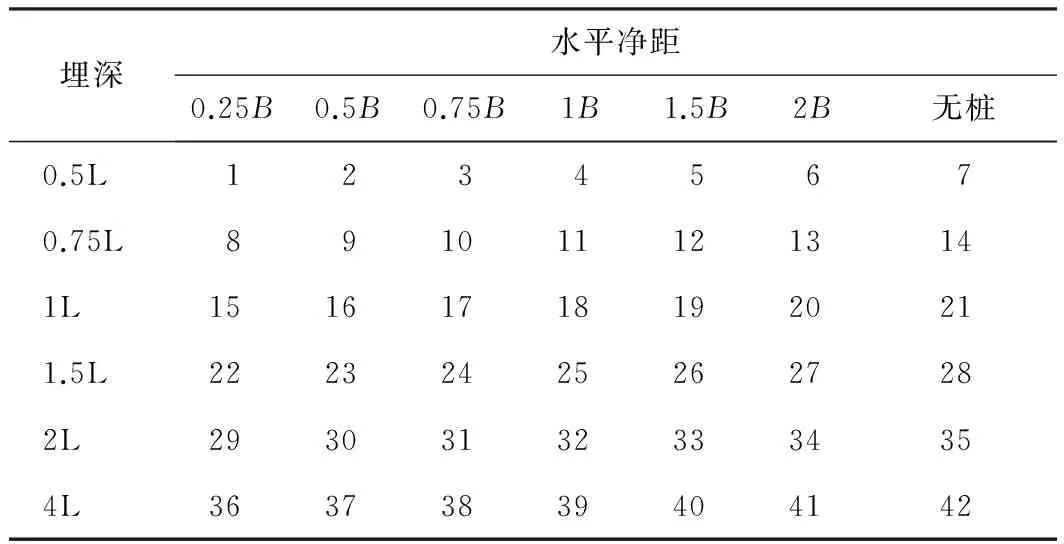
表2 计算工况
2.2 安全系数分布规律分析
结合青岛“上软下硬”地层特点和工程实际情况,桥梁桩基础多采用端承桩的形式,且多以中风化花岗岩作为持力层。本文假设基本模型中桥梁桩长L为18 m,嵌入中风化花岗岩5 m,桩径为1.5 m,隧道跨度B为7 m。当隧道洞身位于桩身、桩底以及超浅埋范围内时,无法采用常规工法进行施工,需单独进行讨论。
利用强度折减法,以隧道拱顶沉降为监测对象,通过试算确定计算无法收敛时对应的强度折减系数范围后,缩小折减系数步距再次计算,以获得更加精确的计算结果。隧道拱顶沉降与强度折减系数关系曲线如图2所示。

图2 拱顶沉降与强度折减系数关系曲线
由图2可知,隧道拱顶沉降在强度折减系数增大至2.436时发生了突变,可认为该隧道的安全系数为2.436。分别对42种工况进行计算,结果如表3所示。

表3 安全系数计算结果
由隧道近接桥梁桩基的安全系数计算结果可知:
1)在埋深不变的情况下,隧道安全系数随距离桩基的水平净距增加在不断增大。当其距离超过某一范围后,安全系数开始趋于稳定,其原因在于桥梁桩基对隧道的影响随着水平净距的增大而不断减弱。
2)随着埋深的增加,隧道安全系数总体呈现出先增大后减小的趋势;但在一定深度范围内隧道与桥梁桩基水平净距越小,这一趋势反而越不明显,说明在隧道近接桥梁桩基施工中,其相互影响程度在隧道安全系数中占主导地位。
3)隧道埋深位于桩底以上时,桥梁桩基对于隧道的安全系数影响较小;隧道埋深位于桩底以下时,隧道安全系数虽然因其埋深有一定增加,但桩体对于隧道安全系数的削弱程度也较前者有明显增加。当隧道埋深继续增加,桩基对于隧道的近接效应又开始逐渐减弱;当埋深超过一定深度,隧道开挖的安全系数不再受桩基的制约。
2.3 影响分区划分
由2.2节计算结果可得到影响系数Ki的分布规律,如表4所示。

表4 影响系数分布情况
使用Matlab自带griddata函数中的4格点样条函数内插[17],对数据点进行补充(即加密数据点),同时根据影响系数Ki的定义将插值结果中大于1的加密点进行修正,然后对所有已知点(原始数据点和加密点)进行多重二次曲面拟合,可得到影响系数空间分布规律图,如图3所示。同时,可通过Matlab将拟合结果进行可视化,如图4所示。

图3 影响系数空间分布图

图4 影响系数插值拟合结果
由图3和图4可以看出: 1)总体上桩基在竖向产生的影响范围和影响程度均大于横向; 2)隧道受影响范围随埋深增加表现出先增大后减小的趋势,当隧道埋深等于L时,受影响范围最大; 3)当隧道位于桩底以上时,水平净距大于1B后,桩基对于隧道的影响可忽略不计; 4)隧道距离桩底越近,受影响程度越大。
通常情况下,任何拟合算法对于已知数据点的数量和分布情况都比较敏感,故对于多重二次曲面拟合效果有必要进行精度与误差检验。重新选取5组工况,对数值模拟和拟合公式得到的影响系数进行对比,如表5所示。

表5 拟合精度分析
结果表明,通过样条函数插值补充的多重二次曲面拟合算法具有较高精度,能够满足工程精度要求。
3 基于桩基受力变形特征的分区优化
3.1 近接施工过程模拟
计算模型土体尺寸为100 m×80 m×40 m,分别约束模型的四周和底面,地表为自由面。土体及初次衬砌采用摩尔-库仑弹塑性模型,桥梁上部结构采用弹性实体单元模拟,桩基础采用pile单元模拟土体与桩之间的相互作用。按照实际施工工序建立主要的施工阶段,如表6所示。

表6 施工工序表
根据桥梁桩基与隧道的相对位置关系,分别建立隧道埋深为1L和2L时,水平净距为0.25B、0.5B、0.75B、1B、1.5B和2B;水平净距为0.25B和2B时,隧道埋深为0.5L、0.75L、1.5L和2L以及无隧道施工干扰下的桥梁共19组不同工况,示意图如图5所示。
模型空间位置图和建模分析图如图6所示。
3.2 计算结果分析
为了避免边界效应,选取距隧道最近的5#桩作为研究对象。隧道开挖完成后,各工况下的桩顶附加沉降和桩顶附加轴力如表7所示。桩基沉降和轴力曲线如图7所示。

(a) 工况分布
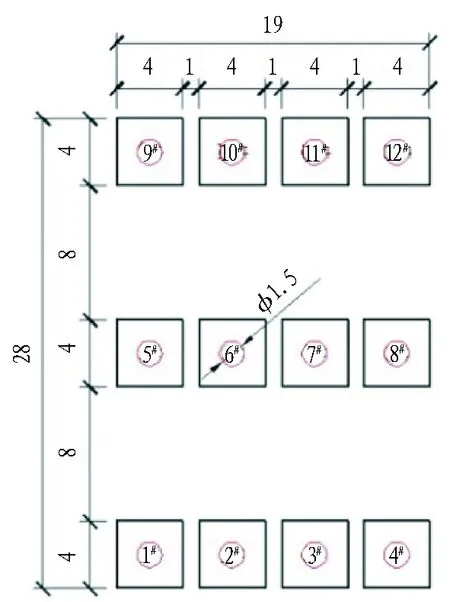
(b) 承台及桩基尺寸(单位: m)
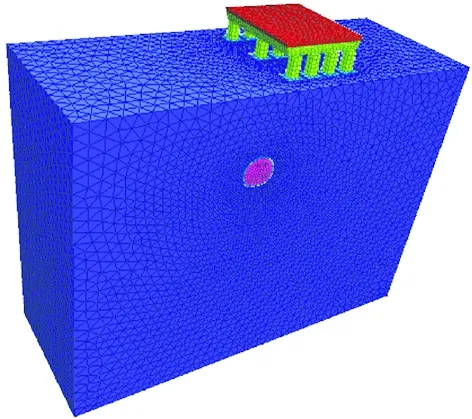
(a) 空间位置图

(b) 内部透视图
Fig. 6 Sketches of relative relationship between tunnel and pile foundations
表7 各工况桥梁桩基计算结果
Table 7 Calculation results of pile foundations in different working conditions
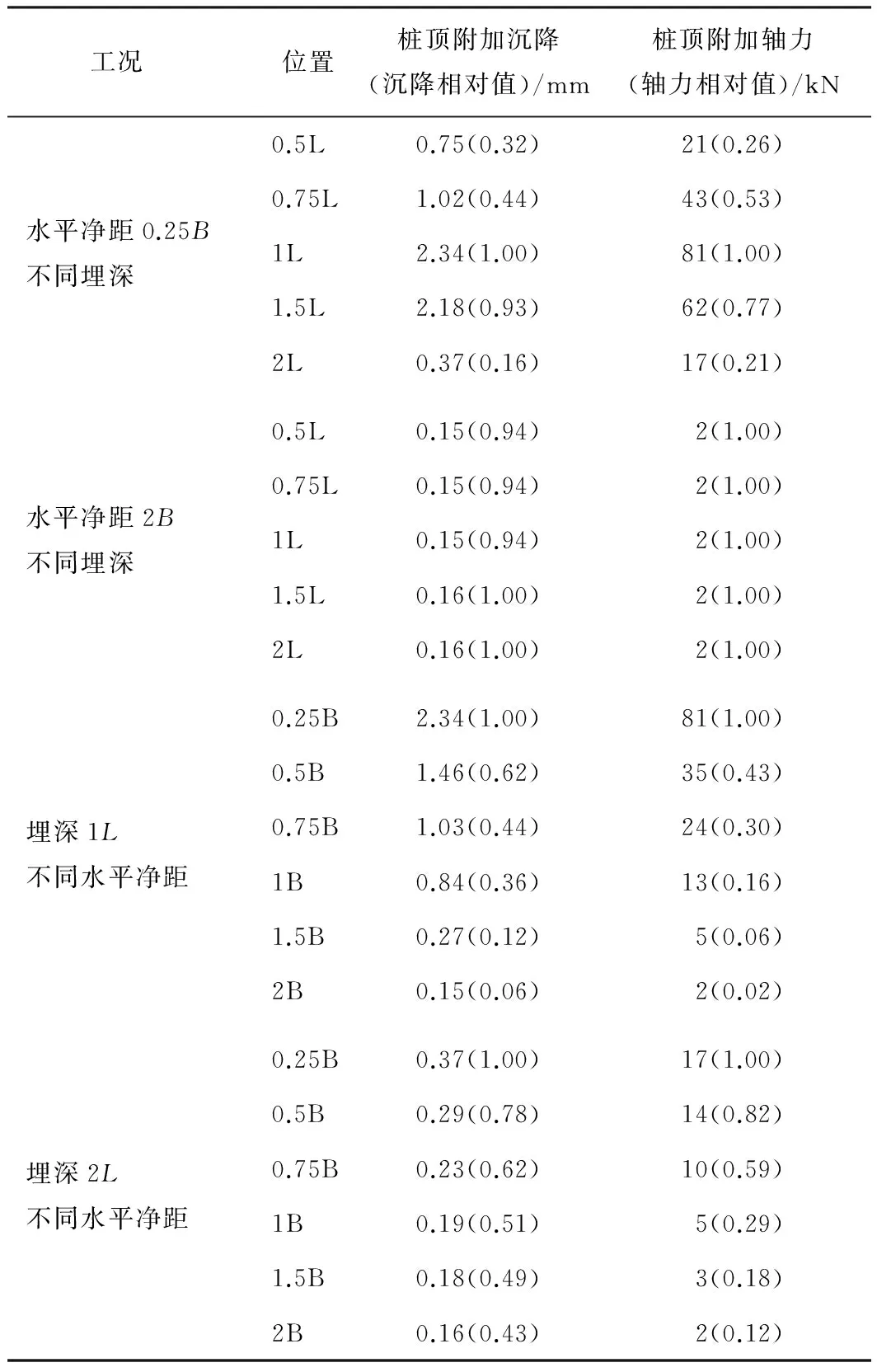
工况 位置桩顶附加沉降(沉降相对值)/mm桩顶附加轴力(轴力相对值)/kN水平净距0.25B不同埋深水平净距2B不同埋深埋深1L不同水平净距埋深2L不同水平净距0.5L0.75(0.32)21(0.26)0.75L1.02(0.44)43(0.53)1L2.34(1.00)81(1.00)1.5L2.18(0.93)62(0.77)2L0.37(0.16)17(0.21)0.5L0.15(0.94)2(1.00)0.75L0.15(0.94)2(1.00)1L0.15(0.94)2(1.00)1.5L0.16(1.00)2(1.00)2L0.16(1.00)2(1.00)0.25B2.34(1.00)81(1.00)0.5B1.46(0.62)35(0.43)0.75B1.03(0.44)24(0.30)1B0.84(0.36)13(0.16)1.5B0.27(0.12)5(0.06)2B0.15(0.06)2(0.02)0.25B0.37(1.00)17(1.00)0.5B0.29(0.78)14(0.82)0.75B0.23(0.62)10(0.59)1B0.19(0.51)5(0.29)1.5B0.18(0.49)3(0.18)2B0.16(0.43)2(0.12)
注: 为便于综合对比分析,将表中数据折算成相对值,见括号内数据。
由计算结果可知: 1)随着隧道埋深的不断增加,在隧道距桩基水平净距仅0.25B时,桩顶沉降和桩顶轴力在1L~1.5L明显增大,对应于影响系数分区图0.75~0.85; 2)当隧道与桩基水平净距达到2B时,桩顶沉降和轴力几乎不受影响,对应于影响系数分区图1以外; 3)当隧道埋深位于1L时,桩顶沉降和桩顶轴力在0.5B水平净距内明显增大,对应于影响系数分区图0.80~0.85; 4)当隧道埋深达到2L时,桩顶沉降和轴力在1B水平净距内虽有一定变化,但变化量不大,对应于影响分区图0.9~1。
为了保证隧道安全修建的同时,桥梁既有结构也能尽可能小地受到影响,根据桥梁桩基受力变形特征对影响分区进行修定: 将影响系数0.8作为强影响区和弱影响区的分界线,影响系数1作为弱影响区和无影响区的分界线。
4 工程实例分析
4.1 工程概况
青岛市红岛—胶南城际(井冈山路—大珠山)轨道交通工程(简称R3线),一期工程建设范围始于开发区的井冈山路,止于新区中心区的大珠山站。工程正线线路全长28.803 km,其中地下线长15.902 km,高架线长12.661 km,设车站12座。地铁区间为单洞单线区间,采用矿山法施工,复合式衬砌暗挖结构。除部分不良地质段外,主要采用台阶法开挖,区间断面形式为马蹄形,采用全包防水。
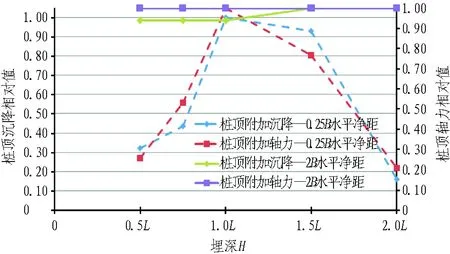
(a) 相同水平净距不同埋深

(b) 相同埋深不同水平净距
在黄东区间隧道开挖过程中,需并行通过张家河桥和柏果树河桥。1)张家河桥(简称A桥)上部结构采用装配式后张法预应力混凝土简支空心板,下部结构采用柱式台、柱式墩,单桩基础(嵌岩桩设计)。桩径 1 000 mm,靠区间正线最近的桩底标高为-8.74 m(嵌入中风化块状流纹岩5.5 m),桩基到区间正线最小水平净距为3.38 m,位于隧道拱顶以上4.66 m。地面标高为5.60 m。2)柏果树河桥(简称B桥)上部结构同样采用装配式后张法预应力混凝土简支空心板,下部结构采用柱式台、柱式墩,单桩基础(嵌岩桩设计)。桩径 1 300 mm,靠区间正线最近的桩底标高为-12.92 m(穿过2 m厚中风化煌斑岩后嵌入微风化煌斑岩1.3 m),桩基到区间正线最小水平净距为5.10 m,位于隧道拱顶以下6.56 m。地面标高为5.62 m。A、B 2桥与区间正线的位置关系如图8所示。

(a) 区间隧道侧穿A桥

(b) 区间隧道侧穿B桥
4.2 影响分区及效果验证
由本文研究成果可知: A桥桩基础与隧道间水平净距为0.49B,隧道埋深为1.32L,影响系数为 0.84,位于弱影响区范围内;B桥桩基础与隧道间水平净距为 0.74B,隧道埋深为0.65L,影响系数为0.97,位于弱影响区范围内。
在施工过程中,对隧道及其周边环境进行了全面的监测,其中桥梁沉降监测点布设于桥梁中跨距离隧道最近的2个墩柱底部,隧道拱顶沉降监测点分别布设于桥梁桩基同一里程断面以及桩基前后50 m断面上。A桥和B桥的墩柱沉降时程曲线如图9所示。
从监测数据可以得知: 在整个施工过程中,A桥墩柱上产生的最大沉降为2.6 mm,B桥墩柱上产生的最大沉降为1.04 mm,A桥墩柱上的沉降值始终大于B桥,但两者均小于相关技术标准及维修养护控制值。

(a) A桥墩柱沉降曲线

(b) B桥墩柱沉降曲线
区间隧道通过A、B 2桥不同断面处的拱顶沉降时程曲线如图10所示。

(a) 隧道侧穿A桥不同断面拱顶沉降曲线
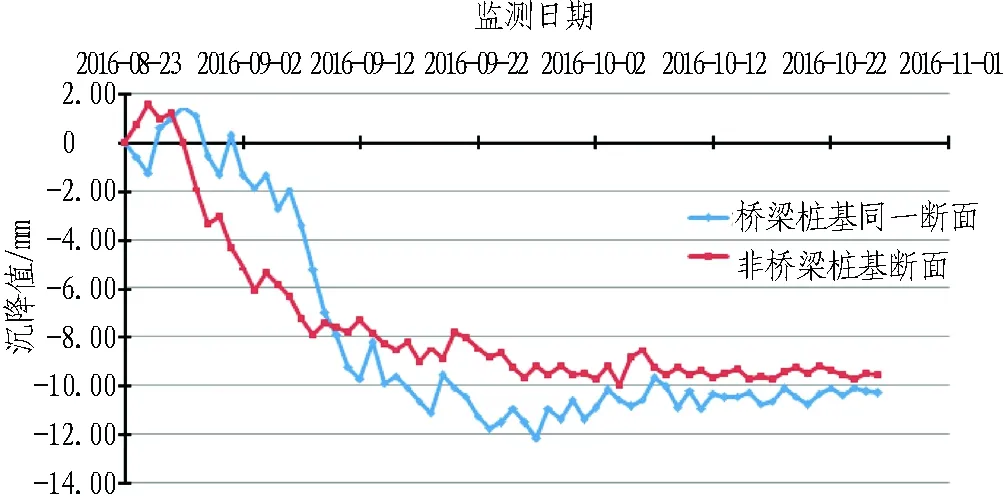
(b) 隧道侧穿B桥不同断面拱顶沉降曲线
从监测数据可以得知: 1)区间隧道通过A桥桩基时,其最大拱顶沉降约为7.1 mm,相对于周围无桥梁桩基时的6.1 mm左右,有14%增幅; 2)区间隧道通过B桥桩基时,其最大拱顶沉降约10.3 mm时趋于稳定,相对于周围无桥梁桩基时的9.5 mm左右沉降,仅有8%增幅,表明区间隧道侧穿A桥时受到的影响较B桥更大; 3)相比于常规地铁施工规定的30 mm沉降警戒值,两者均有较大的富余量。
监测结果表明,地铁区间隧道近接A、B 2桥施工,虽然对桥梁桩基存在一定程度的影响,但影响程度较弱,隧道和既有桥梁始终处于安全状态,与本文结论相符。在实际工程中,在隧道开挖的同时往往还伴随着支护作用,故影响半径可视支护情况进行适当缩小。目前,青岛地铁R3线已全部贯通,A、B 2桥也一直处于正常运营状态。
5 结论与讨论
1)通过对不同空间位置关系下的隧道近接桥梁桩基工程的数值计算,得到了桩基近接影响下的隧道安全系数变化规律,并对其变化规律进行了合理的分析解释。
2)根据以安全系数为基础的影响系数分布规律对上软下硬地层地铁隧道近接桥梁施工影响程度进行了判定,并采用样条函数插值补全和多重二次曲面拟合的方法,给出了影响系数通用分区图,同时结合桩基受力变形特征给出了“强—弱—无影响区”分区标准。对于类似影响分区问题,可采取本文同样的思路和方法进行分析。
3)在上软下硬地层地铁隧道近接桥梁桩基施工中,当隧道埋深位于桩底以上时,几乎只对隧道产生影响且影响较弱;当隧道埋深位于桩底以下时,近接施工对于隧道和桥梁桩基均有不同程度影响,其影响程度在隧道位于桩底时达到最大,且总体上竖向的影响范围和影响程度均大于横向。
4)通过影响分区结论与监测数据对比,验证了本文影响分区的实用性和普遍性,在上软下硬地层地铁隧道近接桥梁桩基施工中具有一定的参考价值。
5)本文以全断面法下的隧道毛洞为研究对象,对于隧道支护形式、支护参数和开挖工法等因素带来的影响未进行详细探讨,有待进一步研究。
[1] 王梦恕. 21世纪我国隧道及地下空间发展的探讨[J]. 铁道科学与工程学报, 2004, 1(1): 7. WANG Mengshu. Development of tunnel and underground space in 21st century in China[J]. Journal of Railway Science and Engineering, 2004, 1(1): 7.
[2] MROUEH H, SHAHROUR I.Three-dimensional finite element analysis of the interaction between tunneling and pile foundations[J].Intemational Joumal for Numerical and Analytical Methods in Geomechanics,2002,26(3): 217.
[3] 郑熹光, 何平, 张安琪, 等. 地铁施工对邻近桥梁桩基础内力影响分析[J]. 现代隧道技术, 2015, 52(3): 110. ZHENG Xiguang, HE Ping, ZHANG Anqi, et al. Influence of metro construction on the internal force of adjacent bridge pile foundation[J].Modern Tunnelling Technology, 2015, 52(3): 110.
[4] 杨超, 黄茂松, 刘明蕴. 隧道施工对临近桩基影响的三维数值分析[J]. 岩石力学与工程学报, 2007, 26(增刊1): 2601. YANG Chao, HUANG Maosong, LIU Mingyun. Three-dimensional numerical analysis of effect of tunnel construction on adjacent pile foundation[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(S1): 2601.
[5] 王成, 徐浩, 郑颖人. 隧道近接桩基的安全系数研究[J]. 岩土力学, 2010, 31(增刊2): 260. WANG Cheng, XU Hao, ZHENG Yingren. Study of safety factor of tunnel close to pile foundation[J]. Rock and Soil Mechanics, 2010, 31(S2): 260.
[6] 唐芬, 郑颖人. 强度储备安全系数不同定义对稳定系数的影响[J]. 土木建筑与环境工程, 2009, 31(3): 61. TANG Fen, ZHENG Yingren. Effect on safety factors in different definitions based on strength margin[J]. Journal of Civil Architectural & Environmental Engineering, 2009, 31(3): 61.
[7] 蒋建平, 章杨松, 罗国煜. 土体宏观结构面及其对土体破坏的影响[J]. 岩土力学, 2002, 23(4): 482. JIANG Jianping, ZHANG Yangsong, LUO Guoyu. Macroscopical structure plane and its influence on failure of soil mass[J]. Rock and Soil Mechanics, 2002, 23(4): 482.
[8] 杨雪强, 朱志政, 韩高升, 等. 不同应力路径下土体的变形特性与破坏特性[J]. 岩土力学, 2006, 27(12): 2181. YANG Xueqiang, ZHU Zhizheng, HAN Gaosheng, et al. Deformation and failure characteristics of soil mass under different stress paths[J]. Rock and Soil Mechanics, 2006, 27(12): 2181.
[9] 郑颖人, 赵尚毅. 有限元强度折减法在土坡与岩坡中的应用[J]. 岩石力学与工程学报, 2004,23(19): 3381. ZHENG Yingren, ZHAO Shangyi. Application of strength reduction fem in soil and rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2004,23(19): 3381.
[10] 郑颖人, 邱陈瑜, 张红, 等. 关于土体隧洞围岩稳定性分析方法的探索[J]. 岩石力学与工程学报, 2008, 27(10): 1968. ZHENG Yingren, QIU Chenyu, ZHANG Hong, et al. Exploration of stability analysis methods for surrounding rocks of soil tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(10): 1968.
[11] 张黎明, 郑颖人, 王在泉, 等. 有限元强度折减法在公路隧道中的应用探讨[J]. 岩土力学, 2007, 28(1): 97. ZHANG Liming, ZHENG Yingren, WANG Zaiquan, et al. Application of strength reduction finite element method to road tunnels[J]. Rock and Soil Mechanics, 2007, 28(1): 97.
[12] 陈力华, 靳晓光. 有限元强度折减法中边坡三种失效判据的适用性研究[J]. 土木工程学报, 2012,45(9): 136. CHEN Lihua, JIN Xiaoguang. Study of the applicability of three criteria for slope instability using finite element strength reduction method[J]. China Civil Engineering Journal, 2012, 45(9): 136.
[13] 仇文革, 章慧健. 硬岩隧道近接高层建筑施工的影响分区研究[C]//第十一届海峡两岸隧道与地下工程学术与技术研讨会论文集. 台湾: 溪头, 2012: 21. QIU Wenge, ZHANG Huijian. Study of influence partition of tunnel constructed approaching to high-rise building in hard rock stratum[C]//Proceedings of The 11th Academic and Technical Symposium on Tunnel and Underground Engineering Across the Strait. Taiwan: Chitou, 2012: 21.
[14] 仇文革. 地下工程近接施工力学原理与对策的研究[D]. 成都: 西南交通大学, 2003. QIU Wenge. The study of mechanics principle and countermeasure of approaching excavation in underground works[D]. Chengdu: Southwest Jiaotong University, 2003.
[15] 孔超, 仇文革, 章慧健, 等. 基于岩石数值极限分析法的洞群围岩稳定性研究[J]. 现代隧道技术, 2013, 50(6): 66. KONG Chao, QIU Wenge, ZHANG Huijian, et al. A study of the rock mass stability of a tunnel group based on numerical limit analysis[J]. Modern Tunnelling Technology, 2013, 50 (6): 66.
[16] 赵仕威, 周小文, 湛杰, 等. 混合多重二次插值在三维地层可视化中的应用[J]. 地下空间与工程学报, 2017, 13(1): 161. ZHAO Shiwei, ZHOU Xiaowen, ZHAN Jie, et al. Application of mixing multiple quadratic interpolation method in 3D stratum visualization[J]. Chinese Journal of Underground Space and Engineering, 2017, 13(1): 161.
[17] SANDWELL D T. Biharmonic spline interpolation of GEOS-3 and SEASAT altimeter data[J]. Geophysical Research Letters, 2013, 14(2): 139.
Study of Impact Partition between Metro Tunnel and Adjacent Bridge Pile Foundation in Upper-soft and Lower-hard Strata
QIU Wenge, LEI Jin*
(KeyLaboratoryofTransportationTunnelEngineering,MinistryofEducation,SchoolofCivilEngineering,SouthwestJiaotongUniversity,Chengdu610031,Sichuan,China)
The safety factor variation laws of tunnel of Hongdao-Jiaonan Intercity Railway in Qingdao laterally crossing adjacent pile foundations of bridges in upper-soft and lower-hard strata are studied by finite element strength reduction method. The results show that: 1) In horizontal direction, the safety factor increases with the increase of horizontal clear distance; and then the safety factor becomes stable when the clear distance reaches the value of tunnel diameter. 2) In vertical direction, with the increasing of the buried depth, the safety factor increases firstly and then decreases. 3) The safety factor of the tunnel would be reduced and the buried depth of the tunnel for reaching maximum safety factor would be increased due to the existence of pile foundations. The interactions between metro tunnel and pile foundations of bridge at different relative positions are as follows: 1) Generally, the vertical interacting scope and degree is larger than the horizontal ones. 2) The tunnel would be affected only if the buried depth of the tunnel is smaller than the buried depth of the pile foundation. 3) The tunnel and the pile foundations would both be affected when the tunnel is under the pile foundation bottom; and the interaction effect reaches peak when the tunnel is right under the pile foundation bottom. The universal sectioning sketch of interacting factor, isogram 0.8 as the boundary of strong interacting zone and weak interacting zone and isogram 1.0 as the boundary of weak interacting zone and non-interacting zone, is given by interpolation method based on polynomial spline method, multiple quadratic surface fitting method and the stress and numerical simulation based deformation characteristics of pile foundation. Finally, the practicability of the study results are testified by comparing sectioning of interacting zones and monitoring results.
tunnel adjacent to pile foundation; upper-soft and lower-hard strata; strength reduction method; safety factor; multiple quadratic surface fitting; impact partition
2017-04-12;
2017-06-10
国家自然科学基金资助项目(51678497, 50878185)
仇文革(1959—),男,山东烟台人,1982年毕业于西南交通大学,隧道与地下铁道专业,博士,教授,主要从事隧道及地下工程方面的教学与研究工作。E-mail: qiuwen_qw@163.com。*通信作者: 雷劲, E-mail: 466399003@qq.com。
10.3973/j.issn.1672-741X.2017.08.001
U 45
A
1672-741X(2017)08-0917-09

