瓦斯异常涌出混沌时间序列预测模型的建立
王菲茵 王启飞 张小千
(中国矿业大学(北京)资源与安全工程学院,北京市海淀区,100083)
★ 煤矿安全 ★
瓦斯异常涌出混沌时间序列预测模型的建立
王菲茵 王启飞 张小千
(中国矿业大学(北京)资源与安全工程学院,北京市海淀区,100083)
运用混沌理论对平煤十矿的实际瓦斯涌出数据进行了分析处理,采用基于关联积分的C-C方法确定了重构空间的时间延迟和嵌入维数,并对时间序列数据进行相空间重构,利用最小数据量法确定了时间序列的最大Lyapunov指数;运用混沌理论加权一阶局域预测方法,建立了混沌时间序列瓦斯异常涌出预测模型;并利用平煤十矿己15-24080掘进工作面31 d的瓦斯实际浓度数据对该模型进行了预测效果检验。结果表明:时间序列的最大Lyapunov指数大于零,证明了时间序列数据具有混沌特征;模型中瓦斯异常涌出的预测发生时间和实际发生时间比较吻合,预测精度达93%。预测模型的可靠性为制定煤矿瓦斯防治措施和采取安全防护措施提供了理论依据。
瓦斯异常涌出 混沌时间序列 相空间重构 最大Lyapunov指数 加权一阶局域预测
矿井瓦斯涌出量预测是瓦斯防治的重要环节,而瓦斯异常涌出可能是煤与瓦斯突出的前兆,对瓦斯异常涌出的预测尤为重要。传统的矿山统计法、分源预测法等不能根据生产条件进行动态跟踪预测,且不能满足综合机械化采煤过程中瓦斯涌出预测精度的要求。瓦斯涌出受自然因素、开采技术、生产工艺等多方面的影响,呈现出复杂的非线性特征,这种非线性特征严重制约着瓦斯涌出预测的准确性,因此对瓦斯涌出非线性特征的研究显得尤为重要。
在非线性混沌理论的基础上,C. Özgen Karacan提出了主成分分析(PCA)和神经网络(ANN)相结合的方法,建立了更为精确的美国长壁煤矿瓦斯涌出预测模型;美国国家职业安全与健康研究所(NIOSH)综合统计、数学、预测和分类ANN方法,开发出实用性强的瓦斯预测和控制(MCP)软件;Cheng Jian等应用倒传递类神经网路(BPNN)、径向基函数神经网络(RBFNN)和最小二乘支持向量机(LS-SVM)分别对瓦斯浓度进行了预测,认为LS-SVM的预测效果最好;张剑英等应用自适应神经模糊推理系统(ANFIS)建立了预测精度高且收敛速度快的煤矿瓦斯浓度预测模型;付华等提出了耦合算法(CIPSO-ENN),结合混沌免疫粒子群算法和Elman神经网络,建立了性能良好的绝对瓦斯涌出量预测模型;王其军等将免疫算法与神经网络理论相结合,提出了预测值和实际值吻合性好的免疫神经网络模型。但上述研究均未对瓦斯数据进行混沌识别。程健、张宝燕等运用加权一阶局域法对瓦斯浓度预测进行了有益的探索,得到了预测误差较小的模型;前者并未对瓦斯异常涌出进行分析,后者是对正常瓦斯浓度值及异常超限瓦斯浓度值分别进行的预测,均不能充分表征实际瓦斯异常涌出的变化情况。
混沌为非线性系统中普遍存在的一种现象,在非线性科学中占有重要地位。它貌似无规则的运动,却在确定性的非线性系统中,不需增加随机因素就出现类似的随机行为,这就是混沌的内在随机性。混沌理论多用于水文、经济、通信、电力、气象等领域的预测,在煤矿中的应用相对较少。本文引入混沌时间序列理论,在相空间重构的基础上,对瓦斯浓度时间序列进行了混沌特征识别,分析了瓦斯浓度和异常涌出的关系,进而实现了对瓦斯异常涌出的预测。
1 时间序列相空间重构
混沌系统中任一分量的演化运动是由与其相互作用的其他多个分量共同决定的。从而,任一分量的发展过程中隐含了这些相关分量的信息。即可从某一分量的一组时间序列数据中提取并恢复出混沌系统原有的规律,此种规律是高维空间中的轨迹。该轨迹经过一段时间的变化后,终将按照有规则的轨迹运动,这就是混沌吸引子。然而,吸引子在经过一系列的转化(如类似拉伸和折叠),形成与时间相关的序列后,会呈现出混乱且复杂的特征。在此引入相空间重构以恢复高维相空间中的混沌吸引子。
F.Takens证明了可以通过找到合适的嵌入维数,并在构建的嵌入维空间里将吸引子恢复。基于此,本文选用了Kim H S,Eykholt R和Salas J D提出的能够同时得出重构相空间的时间延迟τd和嵌入维数m的基于关联积分的C-C方法。具体步骤如下:
(2)定义τ=τd为时间序列的延迟,m为嵌入维数,τw=(m-1)τd为延迟时间窗口,τp(τp≤τw)为平均轨道周期,N为数据集的大小,M=N-(m-1)τ为重构相空间点的个数,则重构相空间为:
(1)
(3)定义嵌入时间序列的关联积分C(无量纲)为:
(2)
式中:θ(x)——Heaviside函数,无量纲,当x≥0时,θ(x)=l,否则θ(x)=0。
定义每个子序列基于关联积分的统计量,用来描述非线性时间序列的相关性S(无量纲):
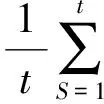
(3)
其中C为关联积分(Correlation integral),因此该方法被称为C-C方法。
(5)选择S(m,N,r,t)的最大值和最小值,定义偏差量ΔS(无量纲)为:
(4)
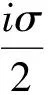
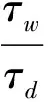
2时间序列混沌特性识别
进行混沌时间序列的预测之前,要判别观测系统的运动形式是否为混沌运动,即进行混沌特性识别。混沌特性识别的定量方法即计算混沌信号奇异吸引子的特性参数,包括Lyapunov指数(表示相邻轨道发散率)、Kolmogorov熵(表示吸引子维数的关联维数和反映信息产生频率)。
Lyapunov指数取值的集合,也就是Lyapunov指数谱,反映了相空间中吸引子的性质,沿某方向的Lyapunov指数λ1为正值,表示在该方向长时间内系统在相空间中相邻轨线上平均发散;为负值,表示平均收敛。
在实际的系统混沌特性识别中仅需计算最大Lyapunov指数λ1,若其为正,则该时间序列为混沌系统。本文采用Rosenstein M.T.等提出的小数据量法计算时间序列的最大Lyapunov指数。该方法对小数据组更为可靠。具体方法如下:
(2)采用上述C-C方法估算出相空间的嵌入维数m和时间延迟τ,根据式(1)进行相空间重构。
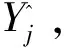
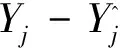
(8)
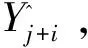
(9)
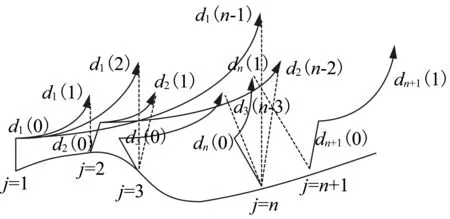
图1 小数据量方法示意图
(5)对每个i,求所有j对应的lndj(i)的平均值y(i),即:
(10)
式中:q——非零的dj(i)的数目。
Δt取1,用最小二乘法做回归直线,该直线的斜率即为最大Lyapunov指数λ1。
3 加权一阶局域法预测模型
混沌预测即在构建的相空间中建立一个非线性模型,并以此模型逼近系统的动态特性,以实现一定短期或长期的预测。模型通常分为以非线性数学模型为基础的动力学方法和以实际观测数据为基础的相空间重构方法。相空间重构中,假设已经获得了完整的观察数据来描述待建的模型物理系统,那么就可不用提前建立主观的模型,直接根据完整的观测数据分析出的客观规律进行时间序列预测,如此避免了预测中的人为主观性,从而可以提高预测精度和可信度。相空间重构的方法的实质是寻找历史上最相似情况。
Farmer J D和Sidorowich J J提出了局域法预测混沌时间序列,取代了全局法原有的对重构相空间的全部状态点进行拟合。局域法的拟合函数是分段函数,能使系统整体的非线性特征更好地体现出来。由于其具有柔韧性好、拟合精度较高且速度较快的特点,本文采用加权一阶局域预测法建立瓦斯异常涌出预测模型。
(1)根据前文计算和分析结果,对瓦斯浓度时间序列进行相空间重构。
(2)局域法里中心点为相空间轨迹的最后一个状态点,记为Yk。计算相空间中所有状态点Yj到中心点Yk之间的欧式距离,且要求满足k-j>P。
取q=m+1个距离最小的Yki(i=1,2,…,q)以确定Yk的参考向量集,Yki到Yk的距离记为di,dm为di的最小值,ε为参数,取ε=1,则定义Yki的权值为:
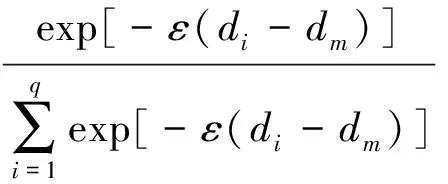
(11)
(3)运用一阶加权局域法进行预测计算。其线性拟合公式如下:
(12)
根据最小二乘原理,求取加权残差平方和f(a,b)的最小值,有:
式(13)作为关于a,b的二元函数,两边同时求偏导并化简,得到关于a和b的方程组:
(14)
求解上述方程组,得到a和b。
(4)将解方程得到的a和b代入式(13),得到预测公式。参考向量为Yki(i=1,2,…,q)的一步预测Yki+1。
4 实例分析
平顶山天安煤业股份有限公司十矿(以下简称平煤十矿)位于河南省平顶山市东北部、平顶山煤田东部,矿井生产能力为290万t/a。目前在800 m埋深以下的采面有8个,最大采深1039 m。引进综合机械化放顶煤后,矿井采用立井、斜井分水平联合开拓,采区上、下山单双翼布置,走向长壁冒落法回采。
己15-24080掘进工作面定期进行预测,超标时进行打钻,不超标时进行掘进,现场记录的掘进速度曲线是忽大忽小的跳动曲线,说明随着采掘作业的进行,工作面应力和瓦斯释放是不均匀的。当现场掘进速度较大,而瓦斯和应力释放速度较小时,应力前移和瓦斯释放不充分容易造成煤与瓦斯突出预测指标超限,因此需根据应力前移和瓦斯释放的速度相应改变掘进速度。
文中仿真数据采用平煤十矿己15-24080掘进工作面1月份的瓦斯浓度。样本共10773 个数据点,采样间隔大约为5 min。当瓦斯浓度变化快时,时间间隔将大大缩短,因此样本不符合时间序列的要求。在此对每小时的瓦斯浓度求平均值,得到时间间隔为1 h、数据量为744的瓦斯浓度数据时间序列,如图2所示。
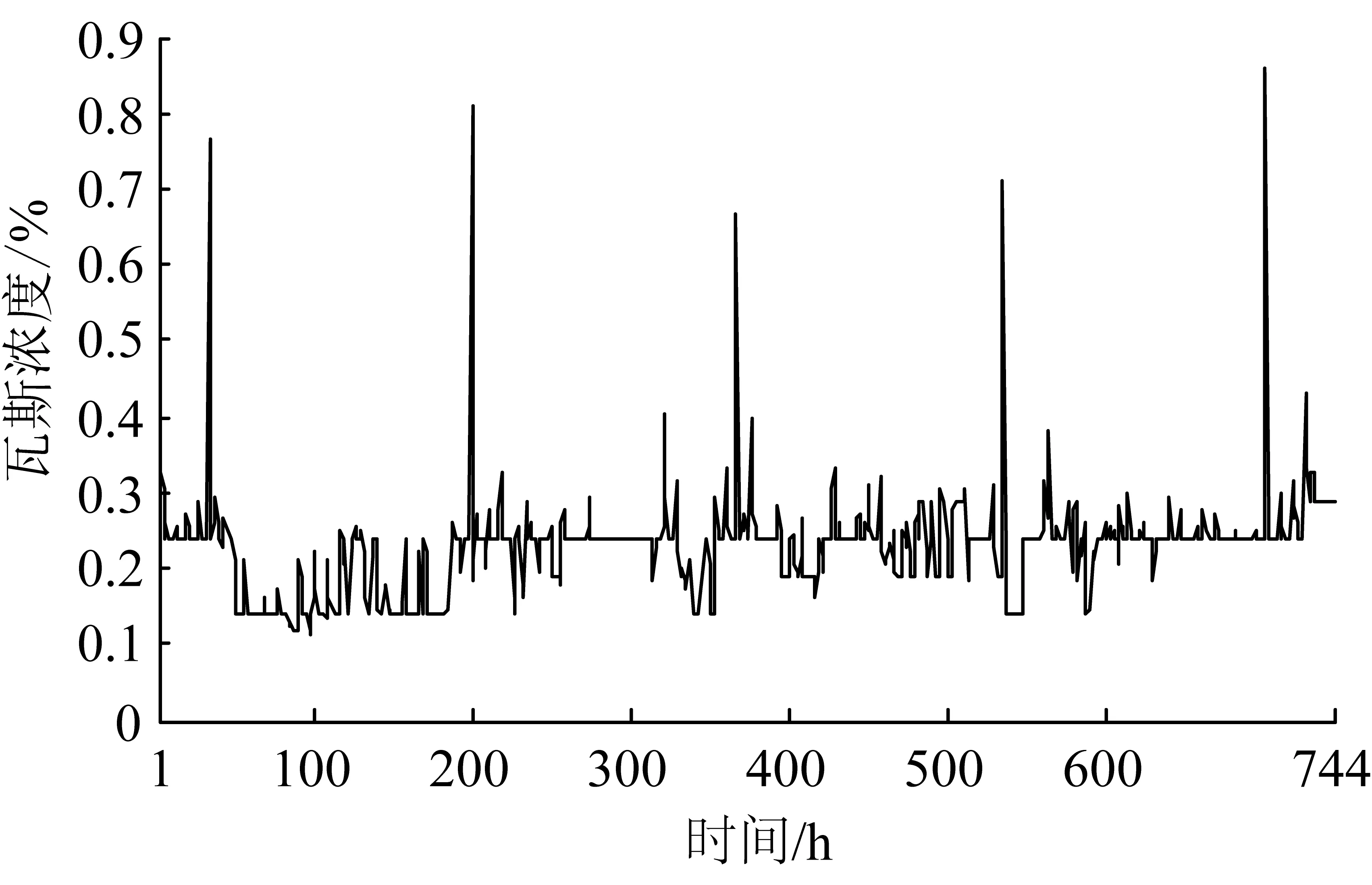
图2 瓦斯浓度数时刻据时间序列
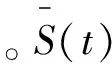
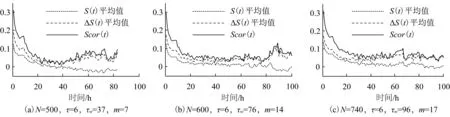
图3 C-C方法估算时间延迟和嵌入维数
根据上述参数,采用小数据量法分别计算出m为7、10、13时最大Lyapunov指数λ1,如图4所示,i为离散时间的步长,y(i)为相空间点的邻点对i个离散时间步后距离的自然对数平均值。对i和y(i)运用最小二乘法做回归直线,回归直线的斜率即为最大Lyapunov指数λ1。计算得出当m=7、10、13时,λ1=6.7×10-5、4.8×10-5、1.5×10-4。由λ1>0,得瓦斯浓度时间序列满足混沌特性识别,视为混沌系统,可以用混沌时间序列理论方法对其进行预测。
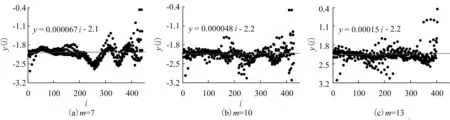
图4 小数据量法计算m不同值时最大Lyapunov指数
瓦斯浓度极值带来的危险性相对较高,其所对应的时刻是危险性相对较大的时刻,亦是瓦斯浓度异常的时刻。由瓦斯浓度和风量可得瓦斯涌出量。因此认为在瓦斯浓度出现极值的时刻,出现了瓦斯异常涌出的情况。
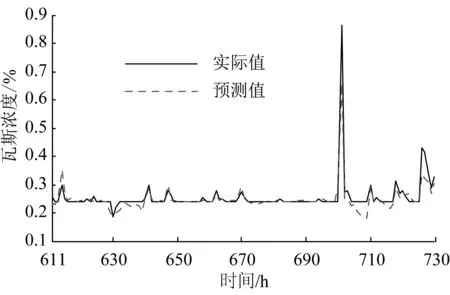
图5 瓦斯异常涌出的模型预测值和实际值
利用上述参数,建立瓦斯异常涌出预测模型。通过计算分析,验证了混沌理论不适用于长期预测,在此取不同的数据量N对序列进行短期预测,并对原始预测值进行延迟修正,分析得出当时间延迟为6、嵌入维数为7时预测效果最好。得出611~730 h时间段120 h的瓦斯异常涌出的预测值与实际值的对比,如图5所示。图5中模型预测值与实际值基本吻合,尤其是瓦斯异常涌出出现的时刻。
预测精度EPA是用来体现预测性能的指标之一,反映了预测值在其均值附近的偏离与实际值在其均值附近的偏离之间的相关性。
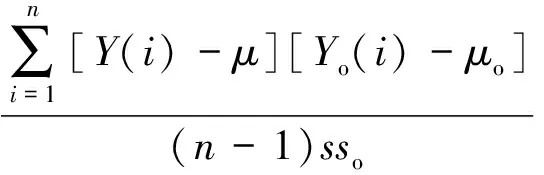
(15)
式中:Y——模型预测序列;
Yo——模型实际值序列;
n——序列的数据量;
μ、μo——预测均值;
s、so——预测标准差。
预测精度EPA取值在-1~1之间,取值为1时,表示预测数据与观测数据分别对自身的均值和标准差归一化后是一样的;预测无误差时EPA值为1。本文对模型预测序列和实际序列的预测精度EPA=93%。
此外,模型预测值的相对误差如图6所示。
在611~730 h时间段120个模型的预测值与实际值的对比中,相对误差在-5%~5%之间的占的72%;相对误差在-10%~10%之间的占87%;相对误差在-15% ~15%之间的占93%。
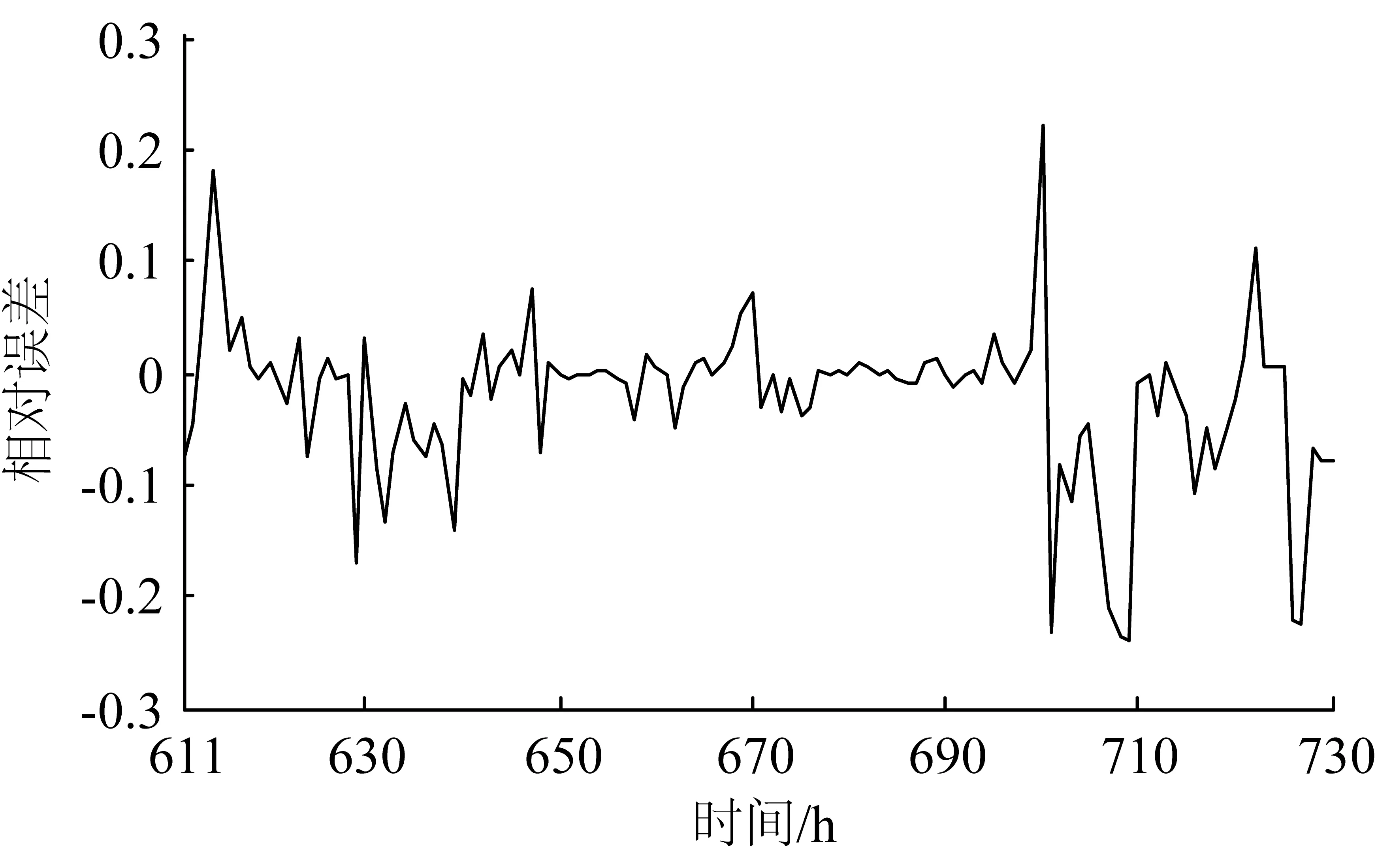
图6 模型预测值的相对误差
考虑到井下瓦斯涌出复杂、工作环境恶劣、监测设备局限等不利因素,在此认为该模型是可靠的,在一定程度上能满足实际需求。
5 结论
(1)确定了瓦斯浓度时间序列相空间重构参数并计算得到最大Lyapunov指数,证明了瓦斯时间序列数据具有混沌特性,为瓦斯异常涌出混沌时间序列预测模型的建立提供了理论依据。
(2)运用混沌理论加权一阶局域预测方法,建立了混沌时间序列瓦斯异常涌出预测模型。
(3)根据平煤十矿己15-24080掘进工作面31 d瓦斯实际浓度数据进行预测效果检验,预测精度达93%,证明了预测模型的可靠行。
(4)预测结果中,瓦斯异常涌出情况的预测时间和实际时间比较吻合,为制定煤矿瓦斯防治措施、防止瓦斯事故的发生提供了理论依据。
[1] 周世宁,林柏泉.煤层瓦斯赋存与流动理论[M].北京:煤炭工业出版社,1999
[2] 施式亮,宋译,何利文等.矿井掘进工作面瓦斯涌出混沌特性判别研究[J].煤炭学报,2006(6)
[3] 王凯,王轶波,卢杰.煤与瓦斯突出动态前兆的非线性特征研究[J].采矿与安全工程学报,2007(1)
[4] 黄为勇,童敏明,任子晖.基于SVM的瓦斯涌出量非线性组合预测方法[J].中国矿业大学学报,2009(2)
[5] 张仕和,才庆祥,陈开岩.基于实时监测数据的综采工作面瓦斯涌出特征分析[J].采矿与安全工程学报,2012(4)
[6] Heather N.Dougherty,Özgen Karacan.A new methane control and prediction software suite for longwall mines[J] .Computers and Geosciences,2011(37)
[7] Cheng Jian,Qian Jiansheng,Guo Yinan.Least squares support vector machine for gas coneentration forecasting in coal mine[J].International Journal of Computer Science and Network Security,2006(6)[8] 张剑英,程健,侯玉华等.煤矿瓦斯浓度预测的ANFIS方法研究[J].中国矿业大学学报,2007(4)
[9] 付华,姜伟,单欣欣等.基于耦合算法的煤矿瓦斯涌出量预测模型研究[J].煤炭学报,2012(4)
[10] 王其军,程久龙.基于免疫神经网络模型的瓦斯浓度智能预测[J].煤炭学报,2008(6)
[11] 程健,白静宜,钱建生等.基于混沌时间序列的煤矿瓦斯浓度短期预测[J].中国矿业大学学报,2008(2)
[12] 张宝燕,李茹,穆文瑜.基于混沌时间序列的瓦斯浓度预测研究[J].计算机工程与应用,2011(10)
[13] 贺昱曜,闰茂德,陈天琴.功率变换器中的混沌及控制方法[J].长安大学学报(自然科学版),2005(6)
[14] 张筑生.微分动力系统原理[M].北京:科学出版社,1987
[15] 陈士华,陆君安.混沌动力学初步[M].武汉:武汉水利电力大学出版社,1998
[16] 张锁春.现代震荡反应的数学理论和数值方法[M].郑州:河南科学技术出版社,1991
[17] 乔美英,陈鑫,兰建义.基于V/S分析的瓦斯涌出量分形特性研究[J].中国煤炭,2014(10)
[18] Kim H S,Eykholt R,Salas J D.Nonlinear dynamics,delay times,and embedding windows[J].Physica D,1999(1-2)[19] W.A.Brock,D.A.Hsieh,B.Le Baron.Nonlinear Dynamics,Chaos,and Instability:Statistical Theory and Economic Evidence[M].Cambridge,MA:MIT Press,1991 [20] W.A.Brock,W.D.Dechert,J.A.Scheinkman, et al.A test for independence based on the correlation dimension[J].Econ.Rev,1996(3)[21] Lai YC,Lerner D.Effective scaling regime for computing the correlation dimension form chaotic time series[J].Physica D,1998(115)
[22] Rosenstein M T,Collins J J,Deluca C J.A practical method for calculating largest Lyapunov exponents from small data sets[J].Physica D,1993(65)
[23] Farmer J D,Sidorowich J.Predicting chaotic time series[J].Physical Review Letters,1987(8)
(责任编辑 张艳华)
中国煤炭杂志投稿须知及防诈骗声明
●投稿方式
《中国煤炭》杂志目前唯一公开使用的投稿专用电子邮箱是mt@zgmt.com.cn,投稿官网为www.zgmt.com.cn;稿件咨询电话为010-84657853;办公地址为北京市朝阳区芍药居35号(100029);开户名为国家安全生产监督管理总局信息研究院,开户银行为交通银行北京育惠东路支行,账号为110060664018000328262。
本刊不收取审稿费用,本刊没有授权其他组织或个人接收、审稿或代发论文,切勿把稿件投到从搜索引擎搜到的或通过其他途径得到的、与上述邮箱、官网不一致的其他邮箱、官网及QQ。请作者投稿、汇款之前认真核实。若邮箱、网址、电话、账户、地址与上述不符,请提防诈骗行为。
●稿件结构
结构完整的稿件应包括:中文标题、作者姓名、工作单位(包括二级单位,邮政编码和所在省、市)、中文摘要、中文关键词、中图分类号(参照中国图书馆分类法,第四版)、文献标识码、英文标题、作者姓名的汉语拼音、工作单位英译名(包括邮政编码和所在城市汉语拼音)、英文摘要、英文关键词、正文、参考文献、作者简介及作者的详细联系方式(详细单位、详细地址、电话、电子邮箱)。请把以上信息依次书写在同一个Word文件内,以提高稿件处理效率。
请把结构完整的稿件的Word版本以附件形式发送到《中国煤炭》杂志的电子邮箱mt@zgmt.com.cn,并在电子邮件的主题中注明“稿件完整题名+作者姓名”。
●版权声明
在《中国煤炭》杂志上发表的文章,被《中国学术期刊(光盘版)》、中国知网、万方数据、中国煤炭网全文收录。稿件一经采用,即视为同意将其网络传播权及电子发行的权利授予本刊。如作者不同意文章编入上述数据库,请在来稿时声明,本刊将做适当处理。
●稿件的录用、退改与退稿
审稿周期是40个工作日。编辑部对决定采用的稿件,以电子邮件方式给作者发送《中国煤炭杂志录稿通知》。如果您想了解审稿及录用情况的,请拨打电话010-84657853与编辑部联系查询。自发稿之日40个工作日内没有收到录稿通知,即为自动退稿,作者可另投他刊。
终审通过的论文,请您不要再把论文投到其他期刊,以免造成一稿多投。稿件发表后,寄送稿酬,并赠送当期刊物2本。
●文责自负原则的重申
依照《著作权法》的有关规定,编辑部可以对来稿作文字修改、删节。
《中国煤炭》杂志对所有论文类投稿通过科技期刊学术不端文献检测系统(AMLC)进行全文比对,检测文字复制率。
Establishmentofpredictionmodelofabnormalgasemissionbasedonchaotictimeseries
Wang Feiyin, Wang Qifei, Zhang Xiaoqian
(School of Resource and Safety Engineering, China University of Mining and Technology, Beijing, Haidian, Beijing 100083, China)
Based on chaos theory, the original gas concentration data of No. 10 Mine of Pingdingshan Tian'an coal industry Co., Ltd, was processed, the phase space of time series was reconstructed after estimating the embedding dimension and delay time through C-C method, and the method of small data was used to calculate the largest Lyapunov exponent. With chaotic adding-weight one-rank local-region method, a prediction model of abnormal gas emission was established. Actual gas concentration data of 24080 driving work face in 31 days was applied to inspect the forecast effect. The results showed that the largest Lyapunov exponent was greater than zero,which illustrated the chaotic characteristics in time series data and the prediction accuracy reached 93%. The reliable prediction model provided theoretical basis in making coal mine gas prevention and control measures and undertaking safety protection.
abnormal gas emission, chaotic time series, phase space reconstruction, largest Lyapunov exponent, adding-weight one-rank local-region method
国家自然科学基金项目(51274206)
王菲茵,王启飞,张小千. 瓦斯异常涌出混沌时间序列预测模型的建立[J].中国煤炭,2017,43(8):138-143,175. Wang Feiyin,Wang Qifei,Zhang Xiaoqian. Establishment of prediction model of abnormal gas emission based on chaotic time series[J]. China Coal, 2017,43(8):138-143,175.
TD712
A
王菲茵(1990-),女,河北邢台人,博士研究生,主要从事矿井灾害防治、数据分析、图像识别、能源经济等方向的研究。

